An evolutionary game for the behavior of third-party evaluators in pension public–private partnership incorporating public participation

ABSTRACT This study analyzes the impact of public participation on the choice of third-party evaluators' behavior strategies during the service quality supervision process of

China's pension public–private partnership project. An evolutionary game model between third-party evaluators and government regulators is developed, wherein the evolution rule of the

two sides and public participation’s influence on their behavior under the two different conditions are analyzed, and a numerical simulation is carried out using MATLAB 2016a. It is found

that third-party evaluators may choose the _false evaluation_ strategy without public participation because of the inducement of rent-seeking or insufficient government punishment when the

regulatory revenue of the government regulatory agencies is less than the regulatory cost. In contrast, in the case of public participation, the _true evaluation_ strategy is chosen with an

improvement in the level of public participation or an increase in reputation incentive. This suggests the construction and improvement of a third-party evaluation system, which shows that

the construction of the service quality supervision system in China’s pension PPP project has a large operating space. SIMILAR CONTENT BEING VIEWED BY OTHERS EVOLUTIONARY GAME ANALYSIS OF

OPPORTUNISTIC BEHAVIOR OF SPONGE CITY PPP PROJECTS: A PERCEIVED VALUE PERSPECTIVE Article Open access 25 May 2022 EVOLUTIONARY GAME ANALYSIS OF ENVIRONMENTAL POLLUTION CONTROL UNDER THE

GOVERNMENT REGULATION Article Open access 10 January 2022 EVOLUTIONARY GAME ANALYSIS ON DECISION-MAKING BEHAVIORS OF PARTICIPANTS IN MEGA PROJECTS Article Open access 07 December 2023

INTRODUCTION Public–Private Partnership (PPP) represents a pioneering collaborative model designed to integrate private investors into the realm of public services and infrastructure

development, a practice increasingly adopted by nations1,2,3. In China, the government has enthusiastically embraced the PPP model within the pension industry, attaining notable milestones

spanning the entire life-cycle of pension PPP projects, from inception to delivery and ongoing operation since 2014. However, limitations regarding regulatory capacity, skilled personnel,

regulatory funding, and other resources have prompted Chinese government bodies to enlist third-party assessment agencies in supervising the service quality of pension PPP projects. These

agencies play a pivotal role in linking operational subsidies of pension PPP projects to their assessment outcomes. This symbiotic relationship serves to mitigate the constraints stemming

from regulatory resource scarcity, while simultaneously generating novel regulatory pressures and deterrent effects. The term "third-party evaluators" alludes to academic

institutions or professional evaluation entities possessing extensive experience in pension service research and adeptness in evaluating the quality of pension services. Nonetheless, within

the PPP framework, characterized by information asymmetry4, third-party evaluators may encounter biases induced by economic incentives from private investors during the evaluation process,

potentially resulting in rent-seeking behaviors and ultimately leading to unscrupulous evaluations. The challenge further manifests as government regulators grapple with an incomplete

understanding of third-party evaluation behavior, thereby engendering potential government failures. As China's pension PPP projects undergo rapid expansion, the imperative of good

governance becomes inexorable for their long-term viability. Embedded within the rubric of good governance lies the essential element of public participation5. To forestall the dissemination

of erroneous information by third-party assessment institutions, governmental oversight, and management of these entities during project service quality evaluations becomes paramount.

Chinese government regulators must galvanize public engagement, encompassing ordinary citizens, the news media, and various societal groups, to partake in evaluations and oversight. The

overarching objective of pension PPP projects resides in furnishing the public with high-quality, cost-effective pension services. Given that public resistance frequently emerges as a

critical factor contributing to project failures6,7, it assumes a pivotal role in ensuring smooth project execution8,9,10,11. The sustainability of pension PPP projects hinges upon public

endorsement of service quality. Consequently, the public can contribute directly or indirectly (via complaints and reports), thus becoming valuable sources of governmental supervision. The

critical inquiry revolves around whether public participation enhances the reliability of third-party evaluations in the oversight of China's pension PPP projects. Moreover, how can a

judicious oversight strategy be crafted that incorporates public participation and incentivize third-party evaluators towards greater responsibility? From a qualitative perspective, it is

imperative to establish effective regulatory mechanisms and precise incentive structures to safeguard the veracity and objectivity of third-party evaluation reports. Initially, evaluators

must undergo oversight through legal frameworks, standard establishment, public engagement, and other measures to obviate the misuse of their regulatory and evaluative informational

advantages in pursuit of rent-seeking and improper interests. Additionally, the establishment of a reputation-based mechanism is imperative for incentivizing third-party evaluators12. This

mechanism would steer them towards objectivity, robust evaluation of information quality, and the disciplining of those who fail in their duties. However, the challenge lies in the

validation of these propositions from a mathematical vantage point. Within the ambit of pension PPP project supervision, government regulators and third-party evaluators grapple with

information asymmetry, culminating in a dynamic, iterative game. This dynamic stems from information incompleteness and is compounded by the cognitive and computational limitations of both

third-party evaluators and government regulators. Given the bounded rationality inherent in these decision-makers, we endeavor to harness evolutionary game theory (EGT) as an analytical

tool. EGT will be employed to dissect how three pivotal factors impact the decision-making proclivities of third-party evaluators: (1) the degree of public participation, (2) the incentive

structure revolving around reputation, and (3) the application of punitive measures. This study endeavors to unravel the mutual evolutionary dynamics of third-party evaluators vis-à-vis

these factors and to proffer a well-grounded supervision strategy that incorporates public engagement, compelling third-party evaluators toward greater accountability. RATIONALE FOR APPLYING

EVOLUTIONARY GAME THEORY (EGT) ACADEMIC PRINCIPLES EGT stands as an exceptionally apt framework for modeling and dissecting complex interactions among strategic agents13. Within PPP

projects, these interactions transcend mere evaluation entities, encompassing government regulators, private investors, and the public. Notably, these stakeholders often harbor divergent

objectives, engendering recurrent and intricate interactions. EGT, with its dynamic and evolving modeling capabilities, provides an indispensable tool for unraveling the nuances of these

multifaceted dynamics. EGT's unique prowess lies in its capacity to capture the adaptive nature of behavior and the learning process over time14. In the specific context of third-party

evaluators, their strategies exhibit a propensity for evolution, influenced by past experiences and the consequences of prior evaluations. This adaptability assumes paramount significance

when deciphering how these evaluators respond to shifts in regulatory policies or variations in the degree of public involvement. EGT offers an established framework for analyzing strategic

decision-making processes15. Third-party evaluators confront strategic dilemmas, oscillating between the delivery of precise assessments that benefit public welfare and the temptation of

engaging in rent-seeking behavior to maximize their profits. Concurrently, government regulators face strategic crossroads regarding supervision strategies. EGT empowers us to model these

strategic choices and illuminate their far-reaching consequences. EGT's utility extends to capturing the intricate dynamics of agent behavior in response to incentives and

penalties16,17. A compelling illustration emerges from a study involving the modeling of interactions among traffic management departments (TMD), drivers, and pedestrians at crosswalks. This

study underscores that, under penalty-incentive control or with robust TMD supervision, drivers willingly yield to pedestrians, potentially enhancing pedestrian safety—a paradigm

particularly pertinent to PPP projects characterized by public scrutiny, concerns about reputation, and the allure of rewards or sanctions. PPP projects, particularly within the pension

sector, carry profound policy implications18. Government policies, regulatory mechanisms, and stakeholder conduct wield substantial influence over project outcomes and sustainability. EGT

offers an indispensable lens through which policymakers and researchers can fathom the consequences of diverse policy choices. Empirical evidence substantiates the applicability of EGT

across a gamut of real-world scenarios encompassing social and economic systems19. Noteworthy research endeavors have harnessed EGT to investigate cooperation, competition, and the emergence

of intricate behaviors in diverse contexts. For instance, resource allocation mechanisms fostering cooperation within well-mixed populations have been examined, effectively addressing

second-order free-rider problems19. This research underlines the efficacy of allocating resources based on individual contributions and rewarding cooperative behavior, underscoring the

relevance of such cooperative strategies in intricate socio-economic environments. Similarly, investigations have delved into the role of monitoring, reporting, and sanctioning mechanisms in

enhancing cooperation amidst collective risk dilemmas18. These studies have illuminated the significance of these mechanisms in comprehending cooperation dynamics, further underscoring the

applicability of EGT. Additionally, explorations into resource allocation strategies in collective-risk social dilemmas have divulged critical insights, demonstrating the emergence of

win–win scenarios promoting cooperation and the sustenance of shared resources under specific conditions20. A remarkable study has probed the efficacy of employing positive and negative

incentives in governing common resources under risky conditions, identifying a local sanctioning scheme combined with pure rewards as the most potent strategy. This approach stimulates

populations towards higher levels of cooperation across diverse parameters and institutional contexts, providing invaluable insights for sustainable resource management policies21. In

summary, the adoption of EGT in understanding the conduct of third-party evaluators within pension PPP projects, particularly in the context of public participation, is richly justified.

EGT's capacity to model intricate interactions, elucidate adaptive behaviors, dissect strategic decision-making, and provide a rigorous framework for comprehending real-world phenomena

finds ample resonance within existing academic research. This alignment underscores the aptness and relevance of EGT as an invaluable tool for advancing our understanding of the intricate

dynamics governing PPP projects. LITERATURE SUPPORT EGT is dedicated to research based on the idea that players cannot fully grasp the entirety of the information, and their decision-making

will change based on updated knowledge22,23. This kind of game theory has achieved success in research on different social fields, such as vaccine dilemma24, sustainable energy

development25, environmental pollution26, sustainable tourism27, rights28, and Social physics29. There are also some scholars using the EGT to research PPP projects under supervision from

different perspectives. Some emphasized the importance of punishment in the supervision of PPP projects30,31,32,33, and some concluded that punishment would be ineffective for private

investors who had violated regulations if government regulators failed to perform their duties34. Others have discussed the importance of public participation and reputation in project

supervision35. However, these studies take private investors as the regulated objects, ignoring other stakeholders’ important roles, such as third-party evaluators and the public, in the PPP

project supervision game mechanism. The behavioral interactions between third-party evaluators and government regulators have a meaningful impact on project supervision. Analyzing the

evolution process and influencing third-party evaluators’ behavior from dynamic and quantitative perspectives is of practical significance. The existing literature exhibits discernible gaps

that, while acknowledging the intricate nature of public participation within our evolutionary game model, underscore the significance of our research. Our contributions are twofold.

Firstly, we scrutinize the dynamic evolutionary trajectory and the influencing variables governing third-party evaluators' conduct without public engagement, delving into micro-level

intricacies. This endeavor bestows upon us a fresh lens through which we can optimize governmental oversight mechanisms. Secondly, we amalgamate evolutionary game theory (EGT) with numerical

simulation methodologies, unraveling the governing dynamics of mutual evolution between government regulators and third-party evaluators. We also evaluate how public participation steers

the behavioral strategies of both parties, thus elevating the current state of research. In summation, our research strives to proffer a novel perspective and theoretical road-map. Our

objective is to optimize governmental oversight mechanisms, foster confidence in third-party evaluations, and achieve the overarching goal of sustainable development for pension

Public–Private Partnership (PPP) projects by instituting a third-party evaluation mechanism integrated with public participation. STRUCTURAL FRAMEWORK The subsequent sections of this paper

are structured as follows: “Rationale for applying evolutionary game theory (EGT)” section: Offers an incisive analysis of the evolutionary game that unfolds between government regulators

and third-party evaluators when public participation is absent. This section delves into the intricate dynamics of their interactions and provides a novel perspective on enhancing

governmental oversight mechanisms. "Construction and analysis of models without public participation" section: Investigates the evolutionary game between government regulators and

third-party evaluators, taking into account the pivotal element of public participation. It delves into the behavioral strategies adopted by these stakeholders in response to public

engagement, shedding light on their dynamics. "Construction and analysis of the public participation model" section: Employs numerical simulation analysis as a validating tool to

assess the efficacy of our model results. This section rigorously examines the outcomes of our research, lending empirical weight to our theoretical framework. "Numerical analysis"

section: Offers conclusive insights drawn from the empirical results, thereby elucidating the policy implications that can be gleaned from our research. We conclude this section by

providing recommendations for future research avenues. This structured framework ensures a comprehensive and academically rigorous exploration of our research agenda, facilitating an

enriched understanding of the complex dynamics inherent in the oversight of pension PPP projects. CONSTRUCTION AND ANALYSIS OF MODELS WITHOUT PUBLIC PARTICIPATION MODEL CONSTRUCTION Suppose

Chinese government regulators entrust third-party evaluators to regularly evaluate the service quality provided by pension PPP projects to ensure maximum public welfare. As the game model

participants, it is assumed that the differences between third-party evaluators and government regulators themselves are not considered. Owing to information asymmetry, both players are

bounded rationally and their objectives are different. Government regulators appeal to society’s overall interests, but third-party evaluators pursue profit maximization. The setting

parameters and descriptions are as follows. Hypothesis 1: Third-party evaluators have two strategic choices: _true evaluation_ (_TE_) _and false evaluation_ (_FE_)_. TE_ indicates that

third-party evaluators hire professional evaluators, use advanced evaluation techniques and uniform evaluation criteria, refuse to rent to private investors, issue an accurate evaluation

report, etc., where \(C_{{\text{t}}}\) is the cost. _FE_ indicates that third-party evaluators hire amateurs for evaluation work, do not use uniform evaluation criteria and advanced

evaluation techniques, accept rent-seeking from private investors, issue false evaluation reports, etc., where \(C_{{\text{f}}}\) is the cost. At this time, \(C_{{\text{t}}} >

C_{{\text{f}}}\). \(R_{t}\) is the revenue that third-party evaluators are entrusted by government regulators to assess. \(R_{r}\) is the rent-seeking income from private investors to

third-party evaluators of _FE_. \(\alpha\)(\({0} \le \alpha \le {1}\)) is the probability that third-party evaluators choose to rent with private investors. \(F_{{\text{t}}}\) is the fine

imposed by the government regulators on third-party evaluators for _FE._ Hypothesis 2: Government regulators also have two choices: _active supervision_ (_AS_) and _negative supervision_

(_NS_). _AS_ indicates that government regulators actively supervise and inspect third-party evaluators’ assessments, regularly comparing the data with the evaluation reports from

third-party evaluators to avoid third-party evaluator violations. _NS_ indicates that government regulators do not supervise and examine third-party evaluations and do not promptly compare

the data with the evaluation reports. \(R_{{\text{g}}}\) is the benefit to be obtained from government regulators choosing _AS_ strategy, such as superior incentives for subordinates,

departmental subsidies, public recognition of government regulators’ supervision, and so on.\(C_{g}\) is the cost of the _AS_ strategy by the government regulators. Hypothesis 3: Under the

_NS_ strategy of government regulators, \(\beta\)(\({0} \le \beta \le {1}\)) is the probability of being discovered by the higher government department, and the loss of third-party

evaluators for _FE_(e.g., government fines, reduced evaluation business volume, revocation of evaluation qualifications, etc.), and \(\beta F_{{\text{g}}}\) is the loss of government

regulators for _NS_. Hypothesis 4: \(x\)(\({0} \le x \le {1}\)) is the probability that third-party evaluators choose the _TE_ strategy; then, \(1 - x\) is the probability of the _FE_

strategy chosen. \(y\) is the probability that government regulators choose the _AS_ strategy, and \(1 - y\) is the probability that the _NS_ strategy is chosen. To simplify the game model,

it is assumed that government regulators can detect the _FE_ of third-party evaluators under _the AS_ strategy, while they cannot under _the NS_ strategy.According to the above assumptions,

we can obtain the evolutionary game payment matrix between third-party evaluators and government regulators without public participation, as shown in Table 1. EVOLUTIONARY STRATEGY STABILITY

ANALYSIS From the above game matrix (Table 1), the expected revenue of _the TE_ strategy selected by third-party evaluators is given by $$E_{x} = y(R_{t} - C_{{\text{t}}} \, ) + (1 -

y)(R_{t} - C_{{\text{t}}} \, )$$ (1) The expected revenue of third-party evaluators choosing the _FE_ strategy is given by $$E_{1 - x} = y(R_{t} { + }\alpha R_{r} - C_{f} - F_{t} ) + (1 -

y)\left( {R_{t} { + }\alpha R_{r} - C_{f} - \beta F_{{\text{t}}} } \right)$$ (2) Then the average expected revenue of third-party evaluators is given by $$\overline{E} = xE_{x} + (1 - x)E_{1

- x}$$ (3) According to the Malthusian dynamic equation36, the replicator dynamic equation for third-party evaluators is given by $$\frac{dx}{{dt}} = x(1 - x)\left( {E_{x} - E_{{1{ - }x}} }

\right) = x(1 - x)[y(1 - \beta )F_{t} - (C_{t} - C_{f} - \beta F_{t} + \alpha R_{{\text{r}}} )]$$ (4) Similarly, the replicator dynamic equation for government regulators is

$$\frac{dy}{{dt}} = y(1 - y)\left( {R_{g} - C_{g} + \beta F_{g} - x\beta F_{g} } \right)$$ (5) Therefore, under the pension PPP model, the evolution of the behavior strategies of third-party

evaluators and government regulators is described by a two-dimensional dynamic system _L__1_ consisting of replicated dynamic Eqs. (4) and (5), that is given by $$\left\{ \begin{aligned}

\frac{{{\text{d}}x}}{dt} & = x(1 - x)[y(1 - \beta )F_{t} - (C_{t} - C_{f} - \beta F_{t} + \alpha R_{r} )] \hfill \\ \frac{dy}{{dt}} &= y(1 - y)(R_{g} - C_{g} + \beta F_{g} - x\beta

F_{g} ) \hfill \\ \end{aligned} \right.$$ (6) Let \(\frac{{{\text{dx}}}}{dt} = 0\); and \(\frac{{{\text{dy}}}}{dt} = 0\), then \((0,0)\),\((0,1)\),\((1,0)\),\((1,1)\) and \(\left(

{\frac{{R_{g} - C_{g} + \beta F_{g} }}{{\beta F_{g} }},\frac{{C_{t} - C_{f} + \alpha R_{r} - \beta F_{t} }}{{F_{{\text{t}}} - \beta F_{{\text{t}}} }}} \right)\) can be obtained by analyzing

the equilibrium point of system _L__1_. However, not all equilibrium points of system _L__1_ can be an evolutionary stable strategy (ESS)37,38. To explore the ESS of system _L__1_, we

analyzed the local stability of the Jacobian matrix of two-dimensional dynamical systems according to the method proposed by Friedman39 and then determined the stability of each equilibrium

point. The Jacobian matrix of the dynamical system _L__1_ is: $$J_{1} = \left[ {\begin{array}{ll} {(1 - 2x)[y(1 - \beta )F_{t} - (C_{t} - C_{f} + \alpha R_{r} - \beta F_{t} )]} & \quad

{x(1 - x)(1 - \beta )F_{t} } \\ { - y(1 - y)\beta F_{g} } & \quad {(1 - 2y)(R_{g} - C_{g} + \beta F_{g} - x\beta F_{g} )} \\ \end{array} } \right]$$ (7) If the following two conditions

are satisfied simultaneously, the equilibrium point of the replicated dynamic equation is the evolutionary stability strategy (ESS). * 1. \({\text{tr}}J = (1 - 2x)[y(1 - \beta )F_{t} -

(C_{t} - C_{f} + \alpha R_{r} - \beta F_{t} )] + (1 - 2y)(R_{g} - C_{g} + \beta F_{g} - x\beta F_{g} ) < 0\) (Trace condition); * 2. \(\det J = (1 - 2x)[y(1 - \beta )F_{t} - (C_{t} -

C_{f} + \alpha R_{r} - \beta F_{t} )](1 - 2y)(R_{g} - C_{g} + \beta F_{g} - x\beta F_{g} ) + xy(1 - x)(1 - y)(1 - \beta )\beta F_{t} F_{g} > 0\) (Jacobian determinant condition) Because

there is \(trJ = 0\) a local equilibrium point \(\left( {\frac{{R_{g} - C_{g} + \beta F_{g} }}{{\beta F_{g} }},\frac{{C_{t} - C_{f} + \alpha R_{r} - \beta F_{t} }}{{F_{{\text{t}}} - \beta

F_{{\text{t}}} }}} \right)\), it is not the equilibrium point of the system evolution stability strategy. Therefore, only \({\text{tr}}J\) and \(\det J\) of the Jacobian matrix at the

remaining four local equilibrium points must be considered. Next, the ESS of system _L__1_ is analyzed in four cases as follows. * Case 1.: When \(F_{t} < C_{t} - C_{f} + \alpha R_{r}\)

and \(R_{g} < C_{g} - \beta F_{g}\) at the same time, \((0,0)\) is the only stable point of system _L__1_. The ESS of system _L__1_ is that third-party evaluators tend to choose the _FE_

strategy, and government regulators tend to choose the _NS_ strategy. According to the two-dimensional dynamic system _L__1_, the sum values of the equilibrium points of Jacobian matrix

_J__1_ are obtained. Furthermore, the local stability of system _L__1_ was determined, as shown in Table 2. * Case 2.: When \(F_{t} < C_{t} - C_{f} + \alpha R_{r}\) and \(R_{g} >

C_{g}\) at the same time, \((0,1)\) is the only stable point of system _L__1_. The ESS of system _L__1_ is that third-party evaluators tend to choose the _FE_ strategy, and government

regulators tend to choose the _AS_ strategy. According to the two-dimensional dynamic system _L__1_, the sum values of the equilibrium points of Jacobian matrix _J__1_ are obtained.

Moreover, the local stability of system _L__1_ was determined, as shown in Table 2. * Case 3.: When \(F_{t} > \frac{{C_{t} - C_{f} + \alpha R_{r} }}{\beta }\) and \(R_{g} < C_{g} -

\beta F_{g}\) at the same time, \((1,0)\) is the only stable point of system _L__1_. The ESS of system _L__1_ is that third-party evaluators tend to choose the _TE_ strategy, and government

regulators tend to choose the _NS_ strategy. According to the two-dimensional dynamic system _L__1_, the sum values of the equilibrium points of Jacobian matrix _J__1_ are obtained.

Furthermore, the local stability of system _L__1_ was determined, as shown in Table 3. * Case 4.: When \(C_{t} - C_{f} + \alpha R_{r} < F_{t} < \frac{{C_{t} - C_{f} + \alpha R_{r}

}}{\beta }\) and \(R_{g} > C_{g}\) at the same time, \((1,1)\) is the only stable point of system _L__1_. The ESS of system _L__1_ is that third-party evaluators tend to choose the _TE_

strategy, and government regulators tend to choose the _AS_ strategy. According to the two-dimensional dynamic system _L__1_, the sum values of the equilibrium points of Jacobian matrix

_J__1_ are obtained. Moreover, the local stability of system _L__1_ was determined, as shown in Table 3. CONSTRUCTION AND ANALYSIS OF THE PUBLIC PARTICIPATION MODEL MODEL CONSTRUCTION In

supervising pension PPP projects, government regulators often need to devote more resources to supervise third-party evaluations due to the complexity of the project organization, high

concealment of rent-seeking behavior, and information asymmetry. From the stability analysis of the evolutionary strategies in Case 1 and Case 3 above, it can be seen that: (1) when

government regulators’ revenue choosing the _AS_ strategy is less than that of choosing the _NS_ strategy (\(R_{{\text{g}}} < C_{g} - \beta F_{g}\)), the phenomenon of _NS_ will occur;

(2) when government regulators are not sufficiently penalizing third-party evaluators, the phenomenon of _FE_ will occur. To effectively solve this problem, the government should allow the

public to directly or indirectly participate in the supervision of pension PPP project service quality to eradicate negative regulatory phenomena caused by insufficient regulatory resources,

and then increase or decrease future cooperation opportunities, according to third-party evaluators’ public reputations. Therefore, the two factors of public participation level and

third-party evaluators’ reputation are introduced into the game process of the two parties to form a new evolutionary game relationship, trying to verify their impact on the strategic

choices of third-party evaluators. For public participation, the setting of the other parameters is as follows. \(\lambda\), where \(0 < \lambda < 1\) is the degree of public

participation. \(\lambda R_{1}\) is third-party evaluators’ additional benefit brought by the government, increasing cooperation opportunities when third-party evaluators gain the public’s

trust and good reputation by choosing the _TE_ strategy. \(\lambda R_{2}\) is the additional loss of third-party evaluators suffered by the government, reducing their cooperation

opportunities when third-party evaluators gain a bad reputation due to _FE_ behavior exposure, and refers to government regulators’ accountability and penalty loss from their superiors due

to being reported for _NS_ by the public. Based on the above assumptions, the evolutionary game payment matrix between third-party evaluators and government regulators with public

participation is shown in Table 4. EVOLUTION STRATEGY STABILITY ANALYSIS According to the Malthusian dynamic equation36, the replicator dynamic equation for third-party evaluators can be

obtained as $$\frac{dx}{{dt}} = x(1 - x)[y(1 - \lambda - \beta )F_{t} + \lambda (R_{{1}} + R_{{2}} + F_{t} ) - (C_{t} - C_{f} + \alpha R_{{\text{r}}} - \beta F_{t} )]$$ (8) Similarly, the

replicator dynamic equation for government regulators is $$\frac{dy}{{dt}} = y(1 - y)[R_{g} - C_{g} + (\lambda + \beta )F_{g} - x(\lambda + \beta )F_{g} ]$$ (9) Therefore, in the PPP model,

the evolution of third-party evaluators and government regulators’ behavioral strategies can be described by the differential equation system _L__2_ consisting of the replicator dynamic Eqs.

 (8) and (9). By analyzing the stable point of system _L__2_, five equalization points can be obtained:\((0,0)\),\((0,1)\)\((1,0)\),\((1,1)\), and \(F_{5} \left( {\frac{{R_{{\text{g}}} -

C_{g} + (\lambda + \beta )F_{g} }}{{(\lambda + \beta )F_{g} }},\frac{{C_{t} - C_{f} + \alpha R_{r} - \beta F_{t} - \lambda (R_{1} + R_{2} + F_{t} )}}{{(1 - \lambda - \beta )F_{t} }}}

\right)\). According to the method proposed by Friedman38, the Jacobian matrix of the differential equation system composed of Eqs. (8) and (9) is $$J_{2} = \left[ {\begin{array}{ll} {(1 -

2x)[y(1 - \lambda - \beta )F_{t} + \lambda (R_{1} + R_{2} + F_{t} ) - C_{t} + C_{f} - \alpha R_{r} + \beta F_{t} ]} & \quad {{\text{x}}(1 - x)(1 - \lambda - \beta )F_{t} } \\ { - y(1 -

y)(\lambda + \beta )F_{g} } & \quad {(1 - 2y)[R_{g} - C_{g} + (1 - x)(\lambda + \beta )F_{g} ]} \\ \end{array} } \right]$$ If the following two conditions are satisfied simultaneously,

the equilibrium point of the replicated dynamic equation is the ESS. * 1. \({\text{tr}}J = (1 - 2x)[y(1 - \lambda - \beta )F_{t} + \lambda (R_{1} + R_{2} + F_{t} ) - C_{t} + C_{f} - \alpha

R_{r} + \beta F_{t} ] + (1 - 2y)[R_{g} - C_{g} + (1 - x)(\lambda + \beta )F_{g} ] < 0\) (Trace condition); * 2. \(\det = (1 - 2x)[y(1 - \lambda - \beta )F_{t} + \lambda (R_{1} + R_{2} +

F_{t} ) - C_{t} + C_{f} - \alpha R_{r} + \beta F_{t} ](1 - 2y)[R_{g} - C_{g} + (1 - x)(\lambda + \beta )F_{g} ] + xy(1 - x)(1 - y)(1 - \lambda - \beta )(\lambda + \beta )F_{t} F_{g} > 0\)

(Jacobian determinant condition). Next, the ESS of system _L__2_ is analyzed in four cases as follows. * Case 5.: When \(F_{t} < C_{t} - C_{f} + \alpha R_{r} ,R_{g} < C_{g} - (\lambda

+ B)F_{g} ,\lambda < \min \left( {\frac{{C_{t} - C_{f} + \alpha R_{r} - F_{{\text{t}}} }}{{R_{{1}} + R_{{2}} }},\frac{{C_{g} - R_{g} - \beta F_{{\text{g}}} }}{{F_{g} }}} \right)\) at the

same time, \((0,0)\) is the only stable point of system _L__2_. The ESS of system _L__2_ is that third-party evaluators tend to choose the _FE_ strategy and government regulators tend to

choose the _NS_ strategy. According to the two-dimensional dynamic system _L__2_, the sum values of the equilibrium points of the Jacobian matrix _J__2_ are obtained, and the local stability

of system _L__2_ is determined, as shown in Table 5. * Case 6.: When \(F_{t} < C_{t} - C_{f} + \alpha R_{r} ,R_{g} > C_{g}\), and \(0 < \lambda < \, \frac{{C_{t} - C_{f} +

\alpha R_{r} - F_{t} }}{{R_{{1}} + R_{{2}} }}\) at the same time, \((0,1)\) is the only stable point of system _L__2_. The ESS of system_ L__2_ is that third-party evaluators tend to choose

the _FE_ strategy and government regulators tend to choose the _AS_ strategy. According to the two-dimensional dynamic system _L__2_, the sum values of the equilibrium points of the Jacobian

matrix _J__2_ are obtained, and the local stability of system _L__2_ is determined, as shown in Table 5. * Case 7.: When \(C_{t} - C_{f} + \alpha R_{r} < F_{t} < \frac{{C_{t} - C_{f}

+ \alpha R_{r} }}{\beta },R_{g} < C_{{\text{g}}} - (\lambda + \beta )F_{g}\), and \(\frac{{C_{t} - C_{f} + \alpha R_{r} - \beta F_{t} }}{{R_{1} + R_{2} + F_{{\text{t}}} }} < \lambda

< \frac{{C_{{\text{g}}} - R_{g} - \beta F_{g} }}{{F_{g} }}\) at the same time, \((1,0)\) is the only stable point of system _L__2_. The ESS of system_ L__2_ is that third-party evaluators

tend to choose the _TE_ strategy and government regulators tend to choose the _NS_ strategy. According to the two-dimensional dynamic system _L__2_, the sum values of the equilibrium points

of the Jacobian matrix _J__2_ are obtained, and the local stability of system _L__2_ is determined, as shown in Table 6. * Case 8.: When \(C_{t} - C_{f} + \alpha R_{r} < F_{t} <

\frac{{C_{t} - C_{f} + \alpha R_{r} }}{\beta },R_{g} > C_{g}\), and \(0 < \lambda < \frac{{C_{t} - C_{f} + \alpha R_{r} - \beta F_{t} }}{{R_{1} + R_{2} + F_{{\text{t}}} }}\) at the

same time,\((1,1)\) is the only stable point of system _L__2_. The ESS of system_ L__2_ is that third-party evaluators tend to choose the _FE_ strategy and government regulators tend to

choose the _AS_ strategy. According to the two-dimensional dynamic system _L__2_, the sum values of the equilibrium points of the Jacobian matrix _J__2_ are obtained, and the local stability

of system _L__2_ is determined, as shown in Table 6. NUMERICAL ANALYSIS Since pension PPP projects and third-party evaluations are still in their infancy in China, it is quite difficult to

obtain relevant data. To better describe the evolution of third-party evaluators and government regulators’ strategic choices under the above two different conditions, we draw on the

numerical examples commonly used by many scholars in applying evolutionary game theory39,40. To make the simulation results more scientific and objective, it is assumed that a Chinese

government regulator entrusts a third-party evaluator to regularly evaluate the service quality provided by the local pension PPP projects, there are 100 beds in the PPP project center of an

old-age institution which collect the elderly with good evaluation ability using market payment. To verify that public participation can effectively prevent third-party evaluators’

rent-seeking behavior, it is assumed that the probability of third-party evaluators’ rent-seeking takes a more considerable value, that is, \(\alpha = 0.6\). Although the parameter

assignment has absolute randomness, it does not affect the simulation results. This section verifies the eight evolutionary stability strategies and discusses the effects of \(F_{t}\),

\(\lambda\), \(R_{1}\), and \(R_{2}\) on the evolution results. VERIFICATION OF EVOLUTIONARY STABILITY STRATEGY CASE Suppose that \(x = 0.1,\;y = 0.1\),\(x = 0.2,\;y = 0.2\),\(x = 0.5,\;y =

0.5\),\(x = 0.6,\;y = 0.6\), and \(x = 0.9,\;y = 0.9\) are five different initial ratios randomly assigned to each game player in the game. The simulation is shown in figures that the

horizontal axis represents _the possibility of TE_ or _AS_ on both sides of the game, while the vertical axis represents the time in months. Suppose that simulated values of parameters in

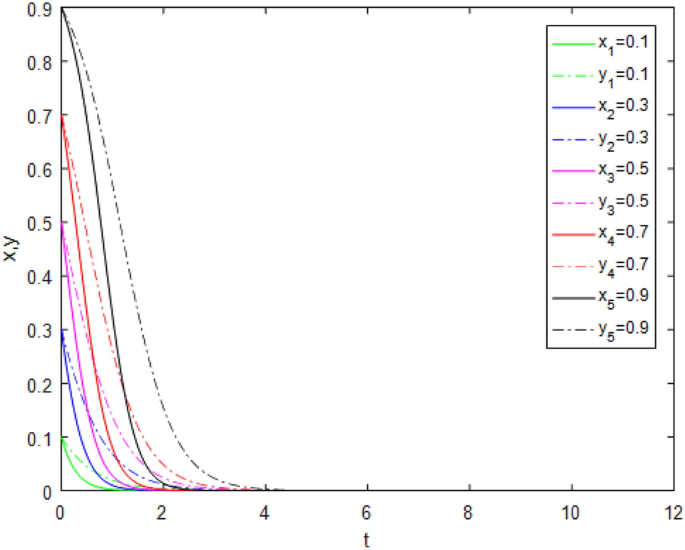
the Case 1 and Case 5 of evolutionary stabilization strategies are listed in Table 7. The simulation is shown in Figs. 1, 2. Both Figs. 1 and 2 show that the game system always tends to

point under different initial ratios, consistent with the analysis of Case 1 and Case 5 respectively. In Case 1 and Case 5, the government’s punishment for third-party evaluator violations

is minimal. Comparing Figs. 1 and 2, it can be seen that Fig. 2 shows the evolution time which _x_ and _y_ are close to 0, is longer when the values of \(\lambda\), \(R_{1}\) and \(R_{2}\)

increase. Although public participation in Case 5 is very high which is difficult to achieve in reality, it does not constitute a deterrent effect for third-party evaluators. Therefore,

third-party evaluators choose the _FE_ strategy. This shows that even if public participation is high, public participation mechanisms will be ineffective if there is no suitable punishment

mechanism. Since the cost of government supervision is far greater than the benefits of supervision, and the penalties imposed by superiors on government regulators for failure to supervise

are minimal, government regulators choose the _NS_ strategy. At this time, the interaction between the two sides develops to the worst balance point, the government supervision mechanism is

in the "invalid" state, and public participation cannot promote the reliability of third-party evaluation institutions. Suppose that simulated values of parameters in the Case 2

and Case 6 of evolutionary stabilization strategies are listed in Table 8. The simulation is shown in Figs. 3, 4. Both Figs. 3 and 4 show that the game system always tends to point \((0,1)\)

under different initial ratios, consistent with the analysis of Case 2 and Case 6 respectively. In Cases 2 and Case 6,the government’s punishment for third-party evaluators’violations is

small, as in Cases 1 and 5. From the comparison of Figs. 3 and 4, it can be found that, when the values of \(\lambda\), \(R_{1}\) and \(R_{2}\) increase, the evolution time which _x_ is

close to 0, is longer. Although public participation in Case 6 is as high as in Case 5, it also does not constitute a deterrent effect for third-party evaluators. Therefore, third-party

evaluators choose the _FE_ strategy. In comparison, the government regulatory revenue is far greater than the regulatory cost, which arouses government regulators’ enthusiasm, so government

regulators choose the _AS_ strategy. At this time, the interaction between the two sides develops into a bad "locked"state. Although government regulators actively supervise and

public participation is also high, the punishment mechanism is not perfect, and third-party evaluators still fail. Suppose that simulated values of parameters in the Case 3 and Case 7 of

evolutionary stabilization strategies are listed in Table 9. The simulation is shown in Figs. 5, 6. Both Figs. 5 and 6 show that the game system always tends to point \((1,0)\) under

different initial ratios, consistent with the analysis of Case 3 and Case 7 respectively. In Case 3, the government strongly punishes third-party evaluators’ illegal behavior. Third-party

evaluators consciously choose the _TE_ strategy, even if government regulators do not supervise. However, it is easy to cause excessive punishment and affect third-party evaluators’

enthusiasm to undertake assessment business. In Case 7, the government moderately punishes the third-party evaluators’ illegal behavior. Under public participation and reputation incentives,

third-party evaluators will actively choose the _TE_ strategy, even if government regulators do not supervise. Therefore, in the case of limited government regulatory resources, public

participation combined with appropriate punishment mechanisms can reduce government regulators’ burden and improve third-party evaluator evaluation reliability. Suppose that simulated values

of parameters in Case 4 and Case 8 of evolutionary stabilization strategies are listed in Table 10. The simulation is shown in Figs. 7, 8. Both Figs. 7 and 8 show that the game system

always tends to point (1,1) under different initial ratios, consistent with the analysis of Cases 4 and 8 respectively. Comparing Figs. 7 and 8, although both show that the "ideal"

state point (1,1) of the game is reached, the game system achieves the ideal goal faster under Case 8 from a time perspective. This shows that public participation can promote a faster and

more benign system transformation. At this time, regulatory resources are fully utilized, the quality of pension services is effectively controlled, social benefits are maximized, and

sustainable and high-quality development of pension PPP projects is realized. CONTRASTIVE ANALYSIS OF EVOLUTION TRAJECTORY Suppose that the initial condition is \(x = 0.5,\;{\text{y}} =

0.5\). First, based on the parameter values under Case1 (i.e., the parameter assignment in Fig. 1), \(F_{{\text{t}}}\) is assumed as a variable, and the MATLAB simulation program is then

carried out. The results are shown in Fig. 9. Second, based on the parameter values in Case 5 (i.e., the parameter assignment in Fig. 2), \(F_{{\text{t}}}\) is assumed as a variable, and the

MATLAB simulation program is performed. The results are shown in Fig. 10. Finally, based on the parameter values under Case 7, that is, the parameter assignment in Fig. 6, \(\lambda\) and

\(R_{1}\) are assumed as variables, and the simulation is compiled. The results are shown in Figs. 11, 12. Figure 9 shows the impact of the penalty parameter \(F_{t}\) changing from 5 to 25

on the system evolution under Case1 conditions. The game system still tends to be stable at point (0,0) when the penalty parameter \(F_{t}\) changes from 5 to 15, while it evolves from point

(0,0) to point (1,0) only when \(F_{{\text{t}}} > 15\). It takes such heavy penalties to effectively restrict third-party evaluators for violations without public participation. Figure 

10 shows the impact of penalty parameters \(F_{t}\) changing from 1 to 5 in the system evolution under Case 5 conditions. The game system still tends to be stable at point (0, 0) when

\(F_{t} < 2\), while it evolves from point (0,0) to point (1,0) only when \(F_{{\text{t}}} \ge 2\). That is, in the case of high levels of public participation, as long as the relatively

light punishment can effectively limit violations of third-party evaluators. It can also be seen from Figs. 9 and 10 that with the increase in \(F_{t}\), the acceleration of the system

converging to point (1,0) gradually decreases. This may be because excessive punishment, to a certain extent, inhibits the enthusiasm of third-party evaluators to adopt the _TE_ strategy,

which leads to a reduction in the marginal effect of punishment measures. Therefore, the punishment mechanism should be reasonable to ensure that its "positive incentive" effect is

brought into full play. Figures 9 and 10 indicate that when government regulators choose the _NS_ strategy, public participation can avoid government regulators’ insufficient punishment and

promote third-party evaluators to choose the _FE_ strategy to a certain extent. This indirectly proves that public participation promotes the reliability of third-party evaluator

evaluations. Figure 11 shows the impact of the public participation coefficient \(\lambda\) changing from 0.1 to 0.5 on system evolution under Case 7 conditions. The game system still tends

to be stable at point (0, 0) when the public participation coefficient \(\lambda\) changes from 0.1 to 0.3, while it starts to evolve positively from point (0,0) to point (1,0) only when

\(\lambda > 0.3\). Figure 11 also shows that the higher the level of public participation, the slower the government regulators tend to choose the _AS_ strategy. This indicates that in

the case of public participation, with the improvement of public participation, even if government regulators fail to supervise, third-party evaluators will choose the _TE_ strategy. This

directly proves that public participation promotes the reliability of third-party evaluations. However, promoting public participation is not easy. It requires a series of government

supporting mechanisms. Figure 12 shows the impact of reputation incentive parameters \(R_{1}\) changing from 0.5 to 2.5 on system evolution under Case 7 conditions. With the strengthening of

the reputation incentive, the game system tends to point (1,0) progressively faster. This indicates that when government regulators choose the _NS_ strategy, third-party evaluators tend to

choose the _TE_ strategy because of the positive strengthening of reputation incentives with public participation. This directly proves that public participation promotes the reliability of

third-party evaluator evaluations. However, reputational incentives cannot be strengthened excessively.A reasonable reputational mechanism should be established to ensure the maximization of

the marginal effects of reputational incentives. Considering the identicality of the parameter trends in other cases, they are not compared in this study. SIMULATION CASE Through the

survey, it is assumed that a third-party evaluator in a province of China obtains the service quality evaluation authority of 20 pension PPP projects in the province through bidding, and the

average income of each project _R__t_ is 20,000 yuan. The value assignment of other parameters without public participation and with public participation is shown in Tables 11 and 12. To

better verify the correctness of the game model, suppose that \(x = 0.1,\;y = 0.2\),\(x = 0.3,\;y = 0.4\),\(x = 0.4,\;y = 0.5\), \(x = 0.6,\;y = 0.7\), and \(x = 0.8,\;y = 0.9\) are five

different initial ratios randomly assigned to each game player in the game. The simulation is shown in Figs. 13, 14. When \(R_{g} < C_{g}\), Fig. 13 shows that the game system tends to be

stable at point (0, 0) without public participation while Fig. 14 shows that the game system tends to be stable at point (0, 1) with public participation. It shows that in the case of

public participation, even if the government chooses the _NS_ strategy, the third-party evaluation agency will also choose the _TE_ strategy under the influence of reputation gains. This

again proves that public participation and reputation incentive have a greater impact on the behavior strategy choice of third-party evaluator. CONCLUSIONS AND IMPLICATIONS CONCLUSIONS Based

on the information asymmetry and the players’ bounded rationality, this study uses evolutionary game theory to establish a game model between government regulators and third-party

evaluators under two different conditions, while comparing and analyzing the evolutionary trends of third-party evaluators’ behavior strategies. Combined with MATLAB simulation analysis, we

conclude that third-party evaluators may choose the _FE_ strategy without public participation because of the inducement of rent-seeking or insufficient government’s punishment when the

regulatory revenue of the government regulatory agencies is less than the regulatory cost. In contrast, in the case of public participation, the _TE_ strategy is chosen with an improvement

in the level of public participation or an increase in reputation incentive. When the cost of government supervision cannot be reduced and government supervision resources are limited, it is

necessary to improve public participation by guiding it to reduce the probability of third-party evaluators adopting the _FE_ strategy based on rent-seeking income. Simultaneously, it is

also necessary to establish a reputation mechanism that spurs third-party evaluators to improve credibility, scientific, and evaluation accuracy. This suggests the construction and

improvement of a third-party evaluation system, which shows that the construction of the service quality supervision system in China’s pension PPP project has a large operating space.

IMPLICATIONS To promote the reliability of third-party evaluation with public participation and improve pension PPP project sustainability, there are several managerial implications for

decision-makers. The first is to establish and improve laws and regulations encouraging public participation. The Chinese government should guide the public to actively participate in

pension PPP project supervision by improving the public participation system and encouraging the public to coordinate public interest and social governance. Simultaneously, the government

should actively establish public participation organizations, encourage and recognize non-profit public participation organizations, and guide the public through grassroots self-governing

organizations, unit trade unions, social welfare organizations, and other types of collective auction participation. Internet public reporting platforms, such as Weibo or WeChat Public

Account, should be set up to provide convenient ways for the public to actively participate in the supervision or reporting of violations by third-party evaluators, reduce the cost and risk

of public reporting, and improve regulatory efficiency. The second is to build a pension PPP project management information system to institute information resource sharing, real-time

display pension service type, charge pension PPP projects based on a public evaluation function, and minimize the information asymmetry between the supervisors and the supervised, which can

provide useful detailed information to third-party evaluators, again reducing costs, and encouraging objective evaluations. The third is to establish and improve the third-party evaluation

system for pension PPP projects’ service quality. As the related service quality evaluation is gradually entrusted to third-party evaluators, the Chinese government should improve the

evaluation mechanism and implementation methods for third-party evaluators, clarify the responsibilities of government regulators, and establish a third-party supervision mechanism. This

should reasonably monitor the third-party evaluation system and formulate a third-party recognition method and system. By horizontally comparing third-party evaluators’ strengths, such as

professional capabilities, staffing, and data processing and monitoring technologies, entry barriers are increased to ensure that only qualified third-party evaluators can obtain evaluation

business. The fourth is to establish an information disclosure mechanism and strengthen the reputation incentive mechanism. Given the professionalism and complexity of service quality

evaluations of pension PPP projects, third-party evaluators have information advantages due to information asymmetry. It is necessary to make full use of big data technology and network

information platforms to promptly publish third-party evaluation reports. This facilitates regulatory supervision, competition, and public involvement, and discloses when third-party

evaluators violate laws or regulations. Simultaneously, reputation factors can be used to restrict third-party evaluators’ behavior and decision-making, and give full play to the public’s

role in supervising third-party evaluators’ behavior. The fifth is to improve third-party evaluators’ reward and punishment mechanisms. This model research also shows that third-party

evaluators will choose the _TE_ strategy when the punishment is strong enough, even if government regulators choose the _NS_ strategy. Therefore, it is necessary to increase the consequences

for third-party evaluators who violate regulations by suspending their qualifications and even canceling the cooperation, while also implementing joint and several liability systems for

injuries to weaken their rent-seeking motivation. Of course, it is also necessary to establish an incentive mechanism to ensure the sustainability of third-party evaluators choosing the _TE_

strategy to provide specific policy subsidies or increase their social recognition and trust. DATA AVAILABILITY The data used to support the findings of this study are included within the

article. REFERENCES * Hwang, B. G., Zhao, X. & Gay, M. J. S. Public private partnership projects in Singapore: Factors, critical risks and preferred risk allocation from the perspective

of contractors. _Int. J. Proj. Manag._ 1(3), 424–433 (2013). Article  Google Scholar  * Wang, Y. Evolution of public–private partnership models in American toll road development: Learning

based on public institutions’ risk management. _Int. J. Proj. Manag._ 33(3), 684–696 (2014). Article  Google Scholar  * Wiewiora, A., Keast, R. & Brown, K. Opportunities and challenges

in engaging citizens in the co-production of infrastructure-based public services in Australia. _Public Manag. Rev._ 18(4), 483–507 (2016). Article  Google Scholar  * Ho, S. P. Model for

financial renegotiation in public-private partnership projects and its policy implications: Game theoretic view. _J. Constr. Eng. M._ 132(7), 678–688 (2006). Article  Google Scholar  *

Menon, S. & Hartz-Karp, J. Institutional innovations in public participation for improved local governance and urban sustainability in India. _Sustain. Earth._ 2(1), 1–19 (2019). Article

  Google Scholar  * Li, Y. _et al._ Government responses to environmental conflicts in urban China: The case of the Panyu waste incineration power plant in Guangzhou. _J. Clean. Prod._ 134,

354–361 (2016). Article  Google Scholar  * Li, C., Li, X. & Wang, Y. Evolutionary game analysis of the supervision behavior for public-private partnership projects with public

participation. _Math. Probl. Eng._ https://doi.org/10.1155/2016/1760837 (2016). Article  MathSciNet  MATH  Google Scholar  * Mumtaz, B. Guiding Cities: The UNDP/UNCHS/World Bank Urban

Management Programme. UN-HABITAT, (2001). * Siemiatycki, M. Delivering transportation infrastructure through public-private partnerships: Planning concerns. _J. Am. Plann. Assoc._ 76(1),

43–58 (2009). Article  Google Scholar  * Ng, S. T., Wong, J. M. W. & Wong, K. K. W. A public private people partnerships (P4) process framework for infrastructure development in Hong

Kong. _Cities._ 31, 370–381 (2013). Article  Google Scholar  * Goodfellow, M. J., Wortley, J. & Azapagic, A. A system design framework for the integration of public preferences into the

design of large infrastructure projects. _Process Saf. Environ._ 92(6), 687–701 (2014). Article  CAS  Google Scholar  * Li, C. & Wang, Q. On third-party evaluation system in the process

of outsourcing government-financed social service for the elderly. _Chin. Public. Adm._ 12, 40–44 (2014). Google Scholar  * Han, J. & Wang, R. Complex interactions promote the frequency

of cooperation in snowdrift games. _Phys. A_ 609, 128386 (2022). Article  MathSciNet  MATH  Google Scholar  * Shamma, J. S. Game theory, learning, and control systems. _Natl. Sci. Rev._

7(7), 1118–1119 (2020). Article  PubMed  Google Scholar  * Kelly, A. Frontmatter. In _Decision Making Using Game Theory: An Introduction for Managers_ (Cambridge University Press, 2003). *

Chen, X. & Szolnoki, A. Punishment and inspection for governing the commons in a feedback-evolving game. _PLoS Comput. Biol._ 14(7), e1006347 (2018). Article  ADS  PubMed  PubMed Central

  Google Scholar  * Chen, L. _et al._ Research on the effectiveness of monitoring mechanisms for “yield to pedestrian”based on system dynamics. _Phys. A_ 591, 126804 (2022). Article  MATH 

Google Scholar  * He, N., Chen, X. & Szolnoki, A. Central governance based on monitoring and reporting solves the collective-risk social dilemma. _Appl. Math. Comput._ 347, 334–341

(2019). MathSciNet  MATH  Google Scholar  * Wang, Q., He, N. & Chen, X. Replicator dynamics for public goods game with resource allocation in large populations. _Appl. Math. Comput._

328(C), 162–170 (2018). MathSciNet  MATH  Google Scholar  * Hu, L. _et al._ Rewarding endowments leads to a win-win in the evolution of public cooperation and the accumulation of common

resources. _Chaos Soliton. Fract._ 134, 109694 (2020). Article  MathSciNet  MATH  Google Scholar  * Sun, W. _et al._ Combination of institutional incentives for cooperative governance of

risky commons. _IScience_ 24(8), 102844 (2021). Article  ADS  PubMed  PubMed Central  Google Scholar  * Gintis, H. _Game Theory Evolving: A Problem-Centered Introduction to Modeling

Strategic Behavior_ (Princeton University Press, 2009). Book  MATH  Google Scholar  * Zhang, M. _et al._ Evolutionary game analysis on strategies in “main manufacturer–supplier” mode

considering technology docking and price concluding under competition condition. _Mathematics._ 7(12), 1184 (2019). Article  Google Scholar  * Kabir, K. M. A. How evolutionary game could

solve the human vaccine dilemma. _Chaos Soliton. Fract._ 152, 111459 (2021). Article  MathSciNet  MATH  Google Scholar  * Wang, G. _et al._ A comprehensive review of research works based on

evolutionary game theory for sustainable energy development. _Energy Rep._ 8, 114–136 (2022). Article  Google Scholar  * Jiang, K. _et al._ Implementation of a multi-agent environmental

regulation strategy under Chinese fiscal decentralization: An evolutionary game theoretical approach. _J. Clean. Prod._ 214, 902–915 (2019). Article  Google Scholar  * He, P., He, Y. &

Xu, F. Evolutionary analysis of sustainable tourism. _Ann. Tourism Res._ 69, 76–89 (2018). Article  CAS  Google Scholar  * Shen, C. _et al._ Exit rights open complex pathways to cooperation.

_J. R. Soc. Interface._ 18(174), 20200777 (2021). Article  PubMed  PubMed Central  Google Scholar  * Jusup, M. _et al._ Social physics. _Phys. Rep._ 948, 1–148 (2022). Article  ADS 

MathSciNet  Google Scholar  * Gao, L. & Zhao, Z. Y. System dynamics analysis of evolutionary game strategies between the government and investors based on new energy power construction

public-private-partnership (PPP) project. _Sustainability_ 10(7), 2533 (2018). Article  Google Scholar  * Liu, J. _et al._ Evolutionary game of investors’ opportunistic behaviour during the

operational period in PPP projects. _Constr. Manag. Econ._ 35(3), 137–153 (2017). Article  Google Scholar  * Guo, B. & Li, J. Research on the evolution of participants collaboration

mechanism in PPP model based on computer simulation: Based on the old community renovation project. _J. Supercomput._ 76(4), 2417–2434 (2020). Article  Google Scholar  * Li, N. & Ma, C.

Evolutionary game analysis on supervision of PPP project tender. In _2018 7th International Conference on Industrial Technology and Management (ICITM)_. 190–193 (IEEE, 2018). * Yue, X. &

Lin, Y. Effectiveness of punishment and operating subsidy in supervision of China’s pension PPP projects: An evolutionary game and simulation analysis. _Math. Probl. Eng._ 2019, 1–12

(2019). Google Scholar  * Wang, G. _et al._ Analysis of private investors conduct strategies by governments supervising public-private partnership projects in the new media era.

_Sustainability_ 10(12), 4723 (2018). Article  Google Scholar  * Weibull, J. W. _Evolutionary Game Theory_ (MIT Press, 1995). MATH  Google Scholar  * Selten, R. A note on evolutionarily

stable strategies in asymmetric animal conflicts. _J. Theor. Biol_ 84(1), 93–101 (1980). Article  ADS  MathSciNet  CAS  PubMed  Google Scholar  * Friedman, D. Evolutionary games in

economics. _Econ. Erica._ 59, 637–666 (1991). MathSciNet  MATH  Google Scholar  * Shan, H. & Yang, J. Promoting the implementation of extended producer responsibility systems in China: A

behavioral game perspective. _J. Clean. Prod._ 250, 119446 (2019). Article  Google Scholar  * Liu, K. _et al._ Evolutionary game and numerical simulation of participants’ collaborative

behavior in integrated project delivery project. _Alex. Eng. J._ 60(1), 373–385 (2021). Article  Google Scholar  Download references FUNDING Funding was provided by the Key Scientific

Research Project of Hunan Provincial Department of Education (No. 21A0531) and the Chenzhou Social Science Planning Project (No. CZSSKL2023093). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS *

School of Economics and Management, Xiangnan University, Chenzhou, 423000, People’s Republic of China Xianghua Yue * School of Management and Economics, Beijing Institute of Technology,

Beijing, 100081, People’s Republic of China Shahzad Khan Durrani * School of Public Policy and Administration, Chongqing University, Chongqing, 400044, People’s Republic of China Shikuan

Zhao * Business School, Hunan Normal University, Changsha, 410000, People’s Republic of China Fuda Li Authors * Xianghua Yue View author publications You can also search for this author

inPubMed Google Scholar * Shahzad Khan Durrani View author publications You can also search for this author inPubMed Google Scholar * Shikuan Zhao View author publications You can also

search for this author inPubMed Google Scholar * Fuda Li View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS Conceptualization, X.H.Y.;

writing—original draft preparation, X.H.Y., F.D.L.; software, X.H.Y., S.K.Z.; writing—review and editing, S.K.D.; supervision, X.H.Y., S.K.D.; F.D.L.; All authors have read and agreed to the

published version of the manuscript. CORRESPONDING AUTHORS Correspondence to Shahzad Khan Durrani or Fuda Li. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing

interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND

PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any

medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The

images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is

not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission

directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Yue, X.,

Durrani, S.K., Zhao, S. _et al._ An evolutionary game for the behavior of third-party evaluators in pension public–private partnership incorporating public participation. _Sci Rep_ 13, 20543

(2023). https://doi.org/10.1038/s41598-023-47369-1 Download citation * Received: 29 December 2022 * Accepted: 13 November 2023 * Published: 23 November 2023 * DOI:

https://doi.org/10.1038/s41598-023-47369-1 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative