H3o+ tetrahedron induction in large negative linear compressibility

ABSTRACT Despite the rarity, large negative linear compressibility (NLC) was observed in metal-organic framework material Zn(HO3PC4H8PO3H)∙2H2O (ZAG-4) in experiment. We find a unique NLC

mechanism in ZAG-4 based on first-principle calculations. The key component to realize its large NLC is the deformation of H3O+ tetrahedron. With pressure increase, the oxygen apex

approaches and then is inserted into the tetrahedron base (hydrogen triangle). The tetrahedron base subsequently expands, which results in the _b_ axis expansion. After that, the oxygen apex

penetrates the tetrahedron base and the _b_ axis contracts. The negative and positive linear compressibility is well reproduced by the hexagonal model and ZAG-4 is the first MOFs evolving

from non re-entrant to re-entrant hexagon framework with pressure increase. This gives a new approach to explore and design NLC materials. SIMILAR CONTENT BEING VIEWED BY OTHERS A LANTHANIDE

MOF WITH NANOSTRUCTURED NODE DISORDER Article Open access 03 April 2025 ENHANCED ELASTIC STABILITY OF A TOPOLOGICALLY DISORDERED CRYSTALLINE METAL–ORGANIC FRAMEWORK Article Open access 23

July 2024 MECHANISTIC INSIGHTS INTO THE DEFORMATION AND DEGRADATION OF A 2D METAL ORGANIC FRAMEWORK Article Open access 01 April 2023 INTRODUCTION Most materials contract in all directions

when hydrostatically compressed. That is the volume (), area () and linear () compressibility are all positive1. Negative volume compressibility is thermodynamically impossible2.

Counterintuitively, negative linear compressibility (NLC) indeed occurs in rare and remarkable crystals1,3,4,5,6. After screening of reported elastic constant tensors from approximately five

hundred crystals, Baughman _et al_. uncovered only 13 compounds showing negative compressibility in simple inorganic or organic compounds1. Among the thirteen crystals, 11 structures were

of monoclinic or lower symmetry. The typical positive linear compressibility (PLC) for crystal material lies in the range _K__l_ ≈ 5–20 TPa−1, with lattice parameter contracting 0.5~2% for

each GPa increase in pressure7. Unfortunately, experimentally determined NLC, for a long time, had been below −2 TPa−1 (−0.2 TPa−1 for LaNbO48, −1.2 TPa−1 for Se9 and −2 TPa−1 for BAsO410).

Until recently, stronger NLC behavior is found: −3.8 TPa−1 for methanol monohydrate from 0 to 0.5 GPa at 160K11, −6.4 TPa−1 for α-BiB3O6 from 0 to 6.5 GPa12, −12 TPa−1 for KMn[Ag(CN)2]3 from

0 to 2.2 GPa13, −41 TPa−1 for [Fe(dpp)2(NCS)2]∙py from 0 to 0.5 GPa14, −42 TPa−1 for Zn[Au(CN)2]2 from 0 to 1.8 GPa15 and −75 TPa−1 for Ag3[Co(CN)6] from 0 to 0.19 GPa7,16. Contrary to

conventional materials, a specific direction of NLC material could not only increase with the increase of hydrostatic pressure, but also remain invariant15. Therefore, NLC is a highly

desirable property exploitable in the development of artificial muscles17, extremely sensitive pressure detectors, shock resistance materials and _etc_. Metal-organic frameworks (MOFs) with

extreme surface area and tunable pore structure have revolutionized the field of crystal engineering18,19,20,21. They consist of metal ions and organic linkers, exhibiting various unique

physical and chemical properties for diverse applications22,23,24. The crystalline order between metals and ligands combined with cooperative structural transformability, forming flexible

and responsive MOFs, namely soft porous frameworks. These materials can respond to mechanical stimuli in a tunable and precise fashion by molecular design, which does not exist for other

known solid-state materials25,26. The elastic behaviour of soft porous crystals is usually complex, such as anisotropic flexibility, negative Poisson’s ration and high NLC25,26,27. The

investigation of MOFs structure deformation under pressure can not only reveal the mechanism of these behaviours, but also can help us design new MOFs with desired mechanical property. The

research of the negative linear/area compressibility of framework materials started very recently28,29,30,31. The first case of NLC in MOFs was [NH4][Zn(HCOO)3], which showed a high degree

of mechanical anisotropy and negative compressibility _K__l_ = −1.8 TPa−1 along its _c_ axis from 0 to 0.94 GPa32. After that, NLC was found in silver(I) 2-methylimidazolate with _K__l_ = 

−4.3 TPa−1 (along _c_ axis, from 0 to 1 GPa)33 and [Ag(en)]NO3-I with _K__l_ = −28.4 TPa−1 (along _a_ axis, from 0 to 0.92 GPa)34. Clearfield and others pioneered named the MOFs formed from

the linker molecules with alkyl chains as zinc alkyl gate(ZAG) because of the likeness of the structure to a child safety gate (Fig. 1(a))21,35. Recently, Gagnon _et al_. measured the

lattice parameters of ZAG-4 under pressure with single crystal X-ray diffraction and observed NLC36,37. The _b_ axis of ZAG-4 increases almost 2% in the range of 1.65–2.81 GPa, indicating a

strong NLC (_K__l_ ≈ −16 TPa−1). Due to the inherently small atomic scattering factor of hydrogen, the exact positions of H2O in ZAG-4 can not be easily detected by X-ray diffraction

technique38. Aurelie U Ortiz _et al_. calculated the ZAG-4 structure under pressure, found a proton transfer and attributed the NLC (from 1.65 to 2.81 GPa) to this structural transition39.

However, PLC was observed after NLC in experiment. This explanation did not answer why NLC and PLC occurs subsequently after proton transfer. Therefore, an unambiguous mechanism for the NLC

in ZAG-4 is still an unresolved matter. Density functional calculation, an integral part of MOFs research, is complementary to experimental techniques and offers invaluable information in

characterization and understanding of systems27,40,41,42. In order to elucidate the NLC mechanism of ZAG-4, we performed the density functional calculation using both PBE and Wu-Cohen (WC)

functional43 as implemented in the Quantum Espresso package44 to determine their atomic structures under pressure. The PBE functional, usually overestimating lattice parameters, has been

widely used in density functional calculations and the WC functional is known to be accurate in predicting solid volumes45,46,47. The wave function was expanded in a plane-wave basis set

with an energy cutoff of 70 Ry and the first Brillouin zone was sampled on a 3 × 3 × 4 mesh. The ultra-soft pseudopotential was used to represent the electron-ion interaction. The

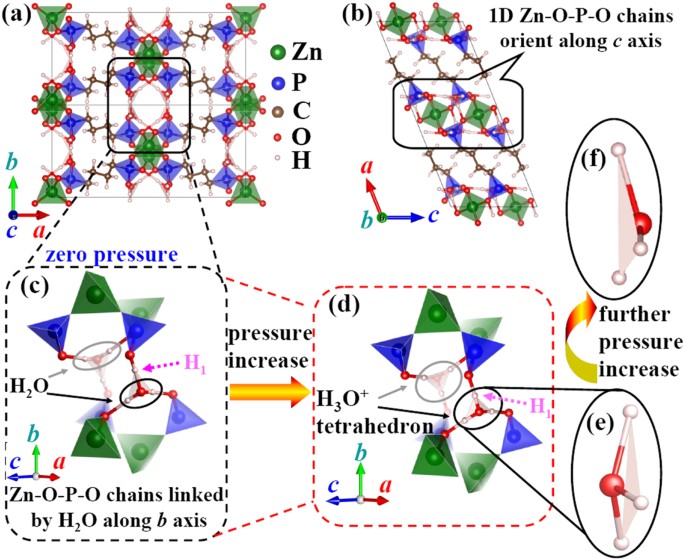
conventional unit cell of ZAG-4 is depicted in Fig. 121,35,36. It has a base-centered monoclinic lattice with the _b_ axis perpendicular to the _a_-_c_ plane. Herein, the three building

blocks of ZAG-4 are the inorganic Zn-O-P-O chains and two bridging ligands (C4H8 and H2O). The 1D Zn-O-P-O chains orient along the _c_ axis and are linked with each other along the _b_ axis

by H2O molecules. So as to give a detailed description of the linkage between H2O molecules and Zn-O-P-O chains, we enlarge the bridging zone in Fig. 1(c). The ZnO4 and PO3C tetrahedrons are

linked along the _c_ axis by sharing oxygen atoms and form the Zn-O-P-O chains. The water molecules are located between two Zn-O-P-O chains. As a result, Zn-O-P-O chains bridged by H2O form

an inorganic 2D structure parallel to the _b_-_c_ plane. Furthermore, the inorganic planes are linked with each other along the _a_ axis by C4H8, which is directly bonded with the P

cations. In brief, the 3D framework is established with the inorganic Zn-O-P-O chains extending along the _c_ axis linked with each other by C4H8 chains and H2O molecules along the _a_ and

_b_ axis, respectively. Firstly, we use the experimental crystal structure at zero pressure as our initial point and fully relax the lattice parameters and atomic positions with PBE

functional. The calculated lattice parameters (_a_ = 19.00 Å, _b_ = 8.41 Å, _c_ = 8.18 Å and volume = 1214.27 Å3) agree well with experimental results (_a_ = 18.51 Å, _b_ = 8.29 Å, _c_ = 

8.27 Å and volume = 1160.55 Å3). As the calculated volume is slight larger than the experimental value, our calculated bulk modulus of (11.6 GPa) is slightly lower than the experimental

result (11.7 GPa). Although it is about one thirty-fifth of the bulk modulus of _sp_3 carbon allotrope (around 400 GPa)48,49, this value is higher than that of porous MOFs MIL-53 and

NH2-MIL-5330,50, but is lower than that of dense MOFs51,52,53,54. In order to explore its NLC mechanism, we applied hydrostatic pressure to ZAG-4 and investigate its structure variation. The

calculated lattice parameters, accompanied with available experimental data36, are shown in Fig. 2. We increase pressure and take the previously optimized structure as the initial point of

higher pressure condition. In this way, we increase pressure to 8 GPa and optimize the structure step by step. As can be seen in Fig. 2, the experimental lattice parameters are well

reproduced by our calculation based on the PBE functional. It is well-known that PBE calculation typically overestimates the lattice parameters by 1–2%. As far as the overestimation is

concerned, our calculated results agree excellently with the experimental data. As pointed by Gagnon _et al_., the alkyl chains serve like a spring cushion and hence contract much under

pressure36. With pressure increasing from zero to 2 GPa, the calculated volume compressibility is around 71 TPa−1 and that of the experimental value from zero to 1.65 GPa is around 69 TPa−1.

The calculated _b_ and _c_ axis have a jump from 2.25 to 2.5 GPa, which is accompanied with the proton transfer. Below 2.25 GPa, the H1 is close to the PCO3 octahedron and far away from the

H2O (Fig. 1(c)). When pressure increases to 2.5 GPa, the proton turns to be close to the H2O and forms the H3O+ tetrahedron. Aurélie U Ortiz _et al_. also found this proton transfer and the

H3O+ tetrahedron formation36,39. They used the wine-rack motif to explain the NLC of ZAG-4 after the proton transition. However, as show in Fig. 2b, NLC does not occur immediately after

proton transfer. Instead, the _b_ axis smoothly expands from 5 to 6.25 GPa (blue shaded area in Fig. 2(b)), which is far away from the proton transfer pressure (2.5 GPa). This indicates that

proton transfer is not enough to lead to the NLC of ZAG-4. There must be something new. We repeat these calculations with the WC functional, because the lattice constants of solids as

determined by it are between LDA and PBE results and on average closer to experiment45,46,47. In the WC results of ZAG-4, the H3O+ tetrahedron is formed at zero pressure. Consequently, the

jump from 2.25 to 2.5 GPa in Fig. 2 does not exist in WC functional results (Supplementary Information). Although the H3O+ is formed at zero pressure, the NLC does not take place immediately

from zero pressure. Instead, the NLC of the _b_ axis occurs in WC functional results from 3.5 to 4.75 GPa. This means the H3O+ tetrahedron and the NLC of _b_ axis are reproduced in WC

functional results as well. We now pay our attention to the changes under pressure of the _b_ axis. The experimentally observed NLC is from 1.65 to 2.81 GPa with the _b_ axis increasing 1.8%

(red shaded area in Fig. 2(b))36. The experimental data are too few (only two) to give a detailed description of the lattice parameters evolution. So as to draw a complete picture, we

calculate the lattice parameters from 5 to 7 GPa with a small pressure step of 0.25 GPa. As shown in Fig. 3(a), the _b_ axis increases from 5 GPa and reaches its maximum at 6.25 GPa.

Accordingly, the average NLC from 5 to 6.25 GPa is −11 TPa−1, as strong as that of KMn[Ag(CN)2]3 (−12 TPa−1, from 0 to 2.2 GPa)13. After that, the _b_ axis decreases with pressure increase

and hence the linear compressibility turns to be positive. It is the deformation of the H3O+ tetrahedron that leads to the NLC of the _b_ axis. As shown in Fig. 1(d,e), the apex oxygen of

the H3O+ tetrahedron is above the H triangle at 5 GPa. The distance (_d_O-H triangle) between the apex oxygen and the H triangle is defined to be positive at this condition (left inset of

Fig. 3(a)). Comparing the left and right inset of Fig. 3(a) (or Fig. 1(e,f)), we find that _d_O-H triangle turns from positive to negative with pressure increase. At the same time, evolution

of _d_O-H triangle is completely accompanied with the evolution of the _b_ axis from expansion to contraction. We also calculate the structure of dehydrated ZAG-4. By deleting the H2O

molecules in ZAG-4 at zero pressure, we get the initial structure of dehydrated ZAG-4. Following the process of Fig. 2, we increase pressure and optimize the structure step by step. The

calculated results (Supplementary Information) show that the _b_ axis of dehydrated ZAG-4 decreases smoothly with pressure increase. This means that the H3O+ tetrahedron deformation is

essential to the NLC of ZAG-4. It is easy to understand the NLC mechanism of ZAG-4 with the following picture in mind. Initially, _d_O-H triangle of the H3O+ tetrahedron is positive at low

pressure. The apex oxygen moves towards the H triangle with pressure increase. It leads to the decrease of _d_O-H triangle (Fig. 3(a)), the area expansion of hydrogen triangle (Fig. 3(b))

and the expansion of the _b_ axis (Fig. 3(a)). Therefore, the NLC of the _b_ axis is directly results from the H3O+ tetrahedron deformation. With further pressure increase, the apex oxygen

penetrates the H triangle and _d_O-H triangle turns to be negative (right inset of Fig. 3(a)). From then on, the apex oxygen moves away from the H triangle. Consequently, both the area of

the H triangle and the _b_ axis decrease with pressure increase. The calculated results using Wu-Cohen functional also show these characteristic features of H3O+ tetrahedron deformation. In

brief, the _b_ axis is expanded by the apex oxygen approaching the H triangle and is contracted by the apex oxygen moving away from the H triangle. There are four microscopic mechanisms

frequently used: (i) ferroelastic phase transition, (ii) polyhedral tilt, (iii) helical system and (iv) wine-rack, honeycomb or related topology.6 The NLC and PLC mechanism of ZAG-4 can be

explained by the hexagonal model55,56. The non re-entrant and re-entrant hexagons are illustrated in the left and right inset of Fig. 4, respectively. The linear compressibility _K__l_ of

this mode can be given analytically as56 in which, as illustrated in the left inset of Fig. 4, _i_ and _h_ are the lengths of the inclined and horizontal ribs, respectively; θ is the angle

between the inclined rib and the vertical direction; φh and φs are the hinging and stretching force constants per unit thickness of the hexagonal plane, respectively. The first term of

equation (1) assumes that ribs are rigid along their lengths and the deflection totally originates from the change of angle θ, while the second one represents that hexagon deforms solely

through stretching of ribs and θ does not change at all. With pressure increase, θ deceases from positive to negative, which is similar to the H3O+ tetrahedron deformation depicted in the

inset of Fig. 3(a). Figure 4 shows the calculated linear compressibility with _i_/_h_ = 3 and φs/φh = 10. Similarly with the _b_ axis evolution in Fig. 3(a), the left side of Fig. 4 is NLC

(34° > θ > 3°) and the right side is PLC (θ < 3°). There are two H3O+ tetrahedrons with positive _d_O-H triangle in Fig. 1(d). This condition is similar to the non re-entrant

hexagon with NLC. When _d_O-H triangle becomes negative, it turns to be similar to the re-entrant hexagon with positive NL. Therefore, the NLC mechanism of ZAG-4 can be simplified to the

hexagonal model. In conclusion, based on the first-principle calculations, we investigated the crystal structure of ZAG-4 under pressure. Our calculated evolutions of the lattice parameters

with pressure excellently agree with the experimental results. The NLC of ZAG-4 occurs in the pressure span of 1.5 GPa (1.16 GPa) with the _b_ axis increasing 1.2% (1.8%) in calculation

(experiment). By inspecting the evolution of atomic position with pressure, we found that the H3O+ tetrahedron deformation is the key point of understanding the large NLC. Initially, with

pressure increase, the apex oxygen moves toward the tetrahedron base and expands the H triangle and the _b_ axis. After penetrating the H triangle, the apex oxygen moves away and then the

_b_ axis contracts with pressure increase. The NLC characteristic of ZAG-4 is well reproduced by the hexagonal model, which gives a vivid explanation for the linear compressibility switch

from negative to positive values. Usually, crystal has either non re-entrant or re-entrant hexagon framework. ZAG-4 is the first MOFs evolving from non re-entrant to re-entrant hexagon

framework with pressure increase. Our finding prescribes a general way to obtain the rare NLC property in complex structures. As H2O molecules abundantly exist in inorganic and organic

materials, it will prompt more investigations on negative compressibility in complex materials57. ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE: Wang, H. _et al_. H3O+ tetrahedron

induction in large negative linear compressibility. _Sci. Rep._ 6, 26015; doi: 10.1038/srep26015 (2016). REFERENCES * Baughman, R. H. Materials with Negative Compressibilities in One or More

Dimensions. Science 279, 1522–1524 (1998). ADS  CAS  PubMed  Google Scholar  * Barnes, D. L., Miller, W., Evans, K. E. & Marmier, A. Modelling negative linear compressibility in

tetragonal beam structures. Mech. Mater. 46, 123–128 (2012). Google Scholar  * Kornblatt, A. J. Materials with Negative Compressibilities. Science 281, 143a–143 (1998). ADS  Google Scholar 

* Lakes, R. & Wojciechowski, K. W. Negative compressibility, negative Poisson’s ratio and stability. Phys. Status Solidi B 245, 545–551 (2008). ADS  CAS  Google Scholar  * Coudert, F. X.

Systematic investigation of the mechanical properties of pure silica zeolites: stiffness, anisotropy and negative linear compressibility. Phys. Chem. Chem. Phys. 15, 16012–16018 (2013). CAS

  PubMed  Google Scholar  * Cairns, A. B. & Goodwin, A. L. Negative linear compressibility. Phys. Chem. Chem. Phys. 17, 20449–20465 (2015). CAS  PubMed  Google Scholar  * Goodwin, A. L.,

Keen, D. A. & Tucker, M. G. Large negative linear compressibility of Ag3[Co(CN)6]. Proc. Natl. Acad. Sci. USA 105, 18708–18713 (2008). ADS  CAS  PubMed  PubMed Central  Google Scholar 

* Mariathasan, J. W. E., Finger, L. W. & Hazen, R. M. High-pressure behavior of LaNbO4 . Acta Crystallogr., Sect. B: Struct. Sci. 41, 179–184 (1985). Google Scholar  * McCann, D. R.

Compressibility of Hexagonal Selenium by X-Ray and Neutron Diffraction. J. Appl. Phys. 43, 1432 (1972). ADS  CAS  Google Scholar  * Haines, J. et al. Collapsing Cristobalitelike Structures

in Silica Analogues at High Pressure. Phys. Rev. Lett. 91, 015503 (2003). ADS  CAS  PubMed  Google Scholar  * Fortes, A. D., Suard, E. & Knight, K. S. Negative linear compressibility and

massive anisotropic thermal expansion in methanol monohydrate. Science 331, 742–746 (2011). ADS  CAS  PubMed  Google Scholar  * Kang, L. et al. Negative linear compressibility in a crystal

of α-BiB3O6 . Sci. Rep. 5, 13432 (2015). ADS  CAS  PubMed  PubMed Central  Google Scholar  * Cairns, A. B., Thompson, A. L., Tucker, M. G., Haines, J. & Goodwin, A. L. Rational design of

materials with extreme negative compressibility: selective soft-mode frustration in KMn[Ag(CN)2]3 . J. Am. Chem. Soc. 134, 4454–4456 (2012). CAS  PubMed  Google Scholar  * Shepherd, H. J.

et al. Antagonism between extreme negative linear compression and spin crossover in [Fe(dpp)2(NCS)2]py. Angew. Chem. Int. Ed. 51, 3910–3914 (2012). CAS  Google Scholar  * Cairns, A. B. et

al. Giant negative linear compressibility in zinc dicyanoaurate. Nat. Mater. 12, 212–216 (2013). ADS  CAS  PubMed  Google Scholar  * Calleja, M., Goodwin, A. L. & Dove, M. T. Origin of

the colossal positive and negative thermal expansion in Ag3[Co(CN)6]: an ab initio density functional theory study. J. Phys.: Condens. Matter 20, 255226 (2008). ADS  Google Scholar  * Aliev,

A. E. et al. Giant-stroke, superelastic carbon nanotube aerogel muscles. Science 323, 1575–1578 (2009). ADS  CAS  PubMed  Google Scholar  * Graham, A. J., Allan, D. R., Muszkiewicz, A.,

Morrison, C. A. & Moggach, S. A. The Effect of High Pressure on MOF-5: Guest-Induced Modification of Pore Size and Content at High Pressure. Angew. Chem. Int. Ed. 50, 11138–11141 (2011).

CAS  Google Scholar  * Tan, J. C. & Cheetham, A. K. Mechanical properties of hybrid inorganic-organic framework materials: establishing fundamental structure-property relationships.

Chem. Soc. Rev. 40, 1059–1080 (2011). CAS  PubMed  Google Scholar  * Costantino, F., Donnadio, A. & Casciola, M. Survey on the phase transitions and their effect on the ion-exchange and

on the proton-conduction properties of a flexible and robust Zr phosphonate coordination polymer. Inorg. Chem. 51, 6992–7000 (2012). CAS  PubMed  Google Scholar  * Gagnon, K. J., Perry, H.

P. & Clearfield, A. Conventional and unconventional metal-organic frameworks based on phosphonate ligands: MOFs and UMOFs. Chem. Rev. 112, 1034–1054 (2012). CAS  PubMed  Google Scholar 

* Gu, Z. Y. & Yan, X. P. Metal-organic framework MIL-101 for high-resolution gas-chromatographic separation of xylene isomers and ethylbenzene. Angew. Chem. Int. Ed. 49, 1477–1480

(2010). CAS  Google Scholar  * Gu, Z. Y., Yang, C. X., Chang, N. & Yan, X. P. Metal-organic frameworks for analytical chemistry: from sample collection to chromatographic separation.

Acc. Chem. Res. 45, 734–745 (2012). CAS  PubMed  Google Scholar  * Gu, Z.-Y., Park, J., Raiff, A., Wei, Z. & Zhou, H.-C. Metal-Organic Frameworks as Biomimetic Catalysts. ChemCatChem 6,

67–75 (2014). CAS  Google Scholar  * Schneemann, A. et al. Flexible metal–organic frameworks. Chem. Soc. Rev. 43, 6062–6096 (2014). CAS  PubMed  Google Scholar  * Li, W., Henke, S. &

Cheetham, A. K. Research Update: Mechanical properties of metal-organic frameworks–Influence of structure and chemical bonding. APL Materials 2, 123902 (2014). ADS  Google Scholar  * Ortiz,

A. U., Boutin, A., Fuchs, A. H. & Coudert, F. X. Anisotropic elastic properties of flexible metal-organic frameworks: how soft are soft porous crystals? Phys. Rev. Lett. 109, 195502

(2012). ADS  PubMed  Google Scholar  * Jiang, X. et al. Isotropic Negative Area Compressibility over Large Pressure Range in Potassium Beryllium Fluoroborate and its Potential Applications

in Deep Ultraviolet Region. Adv. Mater. 27, 4851–4857 (2015). CAS  PubMed  Google Scholar  * Qiao, Y., Wang, K., Yuan, H., Yang, K. & Zou, B. Negative Linear Compressibility in Organic

Mineral Ammonium Oxalate Monohydrate with Hydrogen Bonding Wine-Rack Motifs. J. Phys. Chem. Lett. 6, 2755–2760 (2015). CAS  PubMed  Google Scholar  * Serra-Crespo, P. et al. Experimental

evidence of negative linear compressibility in the MIL-53 metal–organic framework family. Cryst Eng Comm 17, 276–280 (2015). CAS  PubMed  Google Scholar  * Cai, W. et al. Giant negative area

compressibility tunable in a soft porous framework material. J. Am. Chem. Soc. 137, 9296–9301 (2015). CAS  PubMed  Google Scholar  * Li, W. et al. Negative linear compressibility of a

metal-organic framework. J. Am. Chem. Soc. 134, 11940–11943 (2012). CAS  PubMed  Google Scholar  * Ogborn, J. M., Collings, I. E., Moggach, S. A., Thompson, A. L. & Goodwin, A. L.

Supramolecular mechanics in a metal–organic framework. Chem. Sci. 3, 3011 (2012). CAS  Google Scholar  * Cai, W. & Katrusiak, A. Giant negative linear compression positively coupled to

massive thermal expansion in a metal–organic framework. Nat. Commun. 5 1–8 (2014). Google Scholar  * Fu, R.-B. et al. Crystal structures of five transition-metal 1,4-butylenediphosphonates.

Polyhedron 22, 2739–2744 (2003). CAS  Google Scholar  * Gagnon, K. J., Beavers, C. M. & Clearfield, A. MOFs under pressure: the reversible compression of a single crystal. J. Am. Chem.

Soc. 135, 1252–1255 (2013). CAS  PubMed  Google Scholar  * Clearfield, A. Flexible MOFs under stress: pressure and temperature. Dalton Trans. 45, 4100–4112 (2016). CAS  PubMed  Google

Scholar  * Wang, J. et al. Potassium-modified Mg(NH2)2/2 LiH system for hydrogen storage. Angew. Chem. Int. Ed. 48, 5828–5832 (2009). CAS  Google Scholar  * Ortiz, A. U., Boutin, A., Gagnon,

K. J., Clearfield, A. & Coudert, F. X. Remarkable pressure responses of metal-organic frameworks: proton transfer and linker coiling in zinc alkyl gates. J. Am. Chem. Soc. 136,

11540–11545 (2014). CAS  PubMed  Google Scholar  * Odoh, S. O., Cramer, C. J., Truhlar, D. G. & Gagliardi, L. Quantum-Chemical Characterization of the Properties and Reactivities of

Metal-Organic Frameworks. Chem. Rev. 115, 6051–6111 (2015). CAS  PubMed  Google Scholar  * Coudert, F.-X. & Fuchs, A. H. Computational characterization and prediction of metal–organic

framework properties. Coordin. Chem. Rev. 307, 211–236 (2016). CAS  Google Scholar  * Fuentes-Cabrera, M., Nicholson, D. M., Sumpter, B. G. & Widom, M. Electronic structure and

properties of isoreticular metal-organic frameworks: The case of M-IRMOF1 (M = Zn, Cd, Be, Mg and Ca). J. Chem. Phys. 123, 124713 (2005). ADS  PubMed  Google Scholar  * Wu, Z. & Cohen,

R. More accurate generalized gradient approximation for solids. Phys. Rev. B 73, 235116 (2006). ADS  Google Scholar  * Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source

software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009). PubMed  Google Scholar  * Wu, Z. & Cohen, R. E. More accurate generalized gradient

approximation for solids. Phys. Rev. B 73, 235116 (2006). ADS  Google Scholar  * Tran, F., Laskowski, R., Blaha, P. & Schwarz, K. Performance on molecules, surfaces and solids of the

Wu-Cohen GGA exchange-correlation energy functional. Phys. Rev. B 75, 115131 (2007). ADS  Google Scholar  * Bhattacharjee, S., Bousquet, E. & Ghosez, P. Engineering Multiferroism in

CaMnO3 . Phys. Rev. Lett. 102, 117602 (2009). ADS  PubMed  Google Scholar  * Bai, Y. et al. First-principles investigation in the Raman and infrared spectra of _sp_3 carbon allotropes.

Carbon 78, 70–78 (2014). CAS  Google Scholar  * Zhao, Z. et al. Tetragonal allotrope of group 14 elements. J. Am. Chem. Soc. 134, 12362–12365 (2012). CAS  PubMed  Google Scholar  *

Serra-Crespo, P., Stavitski, E., Kapteijn, F. & Gascon, J. High compressibility of a flexible metal–organic framework.Rsc. Adv. 2, 5051–5053 (2012). CAS  Google Scholar  * Tan, J. C.

& Cheetham, A. K. Mechanical properties of hybrid inorganic–organic framework materials: establishing fundamental structure–property relationships. Chem. Soc. Rev. 40, 1059–1080 (2011).

CAS  PubMed  Google Scholar  * Spencer, E. C. et al. Pressure‐Induced Bond Rearrangement and Reversible Phase Transformation in a Metal–Organic Framework. Angew. Chem. Int. Ed. 53, 5583–5586

(2014). CAS  Google Scholar  * Sun, S. et al. Mechanical Properties of a Calcium Dietary Supplement, Calcium Fumarate Trihydrate. Inorg. Chem. 54, 11186–11192 (2015). CAS  PubMed  Google

Scholar  * Feng, G. et al. High pressure behaviour and elastic properties of a dense inorganic–organic framework. Dalton Trans. 45, 4303–4308 (2016). CAS  PubMed  Google Scholar  * Masters,

I. G. & Evans, K. E. Models for the elastic deformation of honeycombs. Compos. Struct. 35, 403–422 (1996). Google Scholar  * Grima, J. N., Attard, D., Caruana-Gauci, R. & Gatt, R.

Negative linear compressibility of hexagonal honeycombs and related systems. Scripta Mater. 65, 565–568 (2011). CAS  Google Scholar  * Momma, K. & Izumi, F. VESTA 3 for three-dimensional

visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011). CAS  Google Scholar  Download references ACKNOWLEDGEMENTS This work is supported by the

National Natural Science Foundation of China (U1404111, 11504089, 21505076) and the Young Scientist Foundation of Henan University of Science and Technology (2013QN026). AUTHOR INFORMATION

AUTHORS AND AFFILIATIONS * School of Physics and Engineering, Henan University of Science and Technology, Luoyang, 471003, China Hui Wang * Department of Physics, Nankai University, Tianjin,

300071, China Min Feng & Yu-Fang Wang * College of Chemistry and Materials Science, Nanjing Normal University, Nanjing, 210023, China Zhi-Yuan Gu Authors * Hui Wang View author

publications You can also search for this author inPubMed Google Scholar * Min Feng View author publications You can also search for this author inPubMed Google Scholar * Yu-Fang Wang View

author publications You can also search for this author inPubMed Google Scholar * Zhi-Yuan Gu View author publications You can also search for this author inPubMed Google Scholar

CONTRIBUTIONS H.W. and M.F. performed the DFT calculations and hexagonal modeling. Y.-F.W. and Z.-Y.G. wrote the main manuscript text and prepared the figures. All authors reviewed the

manuscript. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests. ELECTRONIC SUPPLEMENTARY MATERIAL SUPPLEMENTARY INFORMATION RIGHTS AND PERMISSIONS

This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons

license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to

reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Wang, H., Feng, M.,

Wang, YF. _et al._ H3O+ tetrahedron induction in large negative linear compressibility. _Sci Rep_ 6, 26015 (2016). https://doi.org/10.1038/srep26015 Download citation * Received: 22 February

2016 * Accepted: 22 April 2016 * Published: 17 May 2016 * DOI: https://doi.org/10.1038/srep26015 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this

content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative