Two different approaches for pharmacokinetic modeling of exhaled drug concentrations

ABSTRACT Online measurement of drug concentrations in patient's breath is a promising approach for individualized dosage. A direct transfer from breath- to blood-concentrations is not

possible. Measured exhaled concentrations are following the blood-concentration with a delay in non-steady-state situations. Therefore, it is necessary to integrate the breath-concentration

into a pharmacological model. Two different approaches for pharmacokinetic modelling are presented. Usually a 3-compartment model is used for pharmacokinetic calculations of blood

concentrations. This 3-compartment model is extended with a 2-compartment model based on the first compartment of the 3-compartment model and a new lung compartment. The second approach is

to calculate a time delay of changes in the concentration of the first compartment to describe the lung-concentration. Exemplarily both approaches are used for modelling of exhaled propofol.

Based on time series of exhaled propofol measurements using an ion-mobility-spectrometer every minute for 346 min a correlation of calculated plasma and the breath concentration was used

for modelling to deliver R2 = 0.99 interdependencies. Including the time delay modelling approach the new compartment coefficient ke0lung was calculated to ke0lung = 0.27 min−1 with R2 =

0.96. The described models are not limited to propofol. They could be used for any kind of drugs, which are measurable in patient's breath. SIMILAR CONTENT BEING VIEWED BY OTHERS A

COMPREHENSIVE PHYSIOLOGICALLY BASED PHARMACOKINETIC (PBPK) MODEL FOR NICOTINE IN HUMANS FROM USING NICOTINE-CONTAINING PRODUCTS WITH DIFFERENT ROUTES OF EXPOSURE Article Open access 20

January 2022 DEVELOPMENT OF EXTENDED PHARMACOKINETIC MODELS FOR PROPOFOL BASED ON MEASURED BLOOD AND BRAIN CONCENTRATIONS Article Open access 15 March 2024 DEVELOPMENT AND EVALUATION OF A

HIGH THROUGHPUT INHALATION MODEL FOR ORGANIC CHEMICALS Article 16 June 2020 INTRODUCTION In medicine, drug dosing is usually adapted to patient's weight. However, the blood

concentration of medications varies considerably between different individuals. The blood concentration depends on the liberation, absorption, distribution, metabolism and the excretion of

the drug. These factors are influenced by normal variability of the individual, genetic influences particularly in cytochrome P450 system and organ dysfunctions. These relationships are

described as pharmacokinetics (PK). Different compartment1 and non-compartment PK models e.g. physiological models2 are used to calculate plasma or effect concentrations of drugs. These

models are based on normal population PK data sets. However, the concentrations are only calculated and the difference to the real drug blood concentration could be substantially3. The

measurement of blood concentration e.g. by High-Performance Liquid Chromatography (HPLC) is expensive, complex and has a time delay of several hours. In clinical practise the measurement of

blood concentrations is only performed for a few drugs4. Therefore, a new promising approach is the online measurement of drug concentrations in patient's breath5. Until now, the number

of drugs which were detected in patient's breath is limited: e.g. methadone6, propofol7, valproic acid8. Actually, different methods are under consideration, including mass

spectrometry, ion mobility spectrometry and chemical sensors. In the present paper, we will not focus on the experimental details, conditions, advantages and disadvantages of the different

methods. The starting condition is, that such measurements can be carried out and time series of breath concentration values are available within short time intervals. Acceptable would be

the range of one value per minute of exhaled breath concentration, with a total analysis time in the same range of 1 minute. Consequently, one value each minute with 1 minute retarding will

be considered as provided by an experimental breath analysis method. However, a direct transfer between breath concentration and blood concentration is not possible and leads to poor

correlation values, because the diffusion of drugs through the capillary wall of the alveoli takes time. If the drugs blood concentration increases or decreases the exhaled concentration

follows with a time delay9. Classically the diffusion of a drug from blood through the lung into air is described by the blood/gas partition coefficient (Ostwald Coefficient). This

coefficient is defined as the ratio of the concentration in blood to the concentration in gas that is in contact with that blood when the partial pressure in both compartments is at

equilibrium. It is thus a dimensionless number. The higher the blood/gas partition coefficient, the more soluble is the anaesthetic in blood compared to air and the more it binds to lipids

and proteins in the blood. If an anaesthetic has a high Ostwald coefficient, then a large amount of it will have to be taken up in the body's blood before being passed on to the fatty

(lipid) tissues of the brain where it can exert its effect10. The blood/gas partition coefficient is widely used for the PK description of volatile anaesthetics10. However, for PK modelling

the coefficient could only be used if the partial pressure in both compartments is at equilibrium. Depending on the drug it could take several hours to reach this steady state. Therefore,

the introduction of breath concentrations measured within time series needs a model to include the concentration values measured in breath without the precondition of compartments within

equilibrium. To overcome the precondition of equilibrium, we would like to demonstrate in this manuscript two different PK modelling approaches to handle the drug breath concentrations. The

calculations are performed on the basis of concentration data of the measurements of a patient, who received the intravenous anaesthetic propofol. The propofol breath concentration was

measured by a modified ion mobility spectrometer combined with a multi-capillary-column (P-IMS)11, which delivers one peak analysis every minute with 1 minute total analysis time including

sampling of 10 mL exhaled breath. It should be noted, that the presented models are not specific for propofol. In principle, the mathematical descriptions could also be used for other drugs.

METHODS CLINICAL MEASUREMENTS With approval of the local Ethics Committee (Ärztekammer des Saarlandes, Saarbrücken, Germany) and written informed consent an adult patient scheduled for an

abdominal surgical procedure was studied. The patient received propofol and remifentanil (opioid) as a target controlled infusion (TCI). The concept of TCI is to estimates calculated plasma

and effect site concentrations based on pharmacokinetic 3 compartment model12. The breath concentration values were measured using an ion mobility spectrometer type BioScout (B&S

Analytik GmbH, Dortmund, Germany), with the internal Multi-capillary-column (MCC) adjusted to 90°C to reach a retention time of propofol on the MCC (type OV-5, Multichrom, Novosibirsk,

Russia) of about 20 s. A total volume of 10 mL was taken on the MCC. For further details considering the method see11, for the experimental setup see13. Samples of exhaled air were

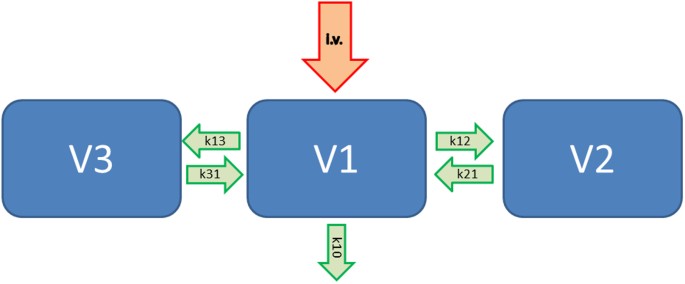
automatically taken every minute by the P-IMS. A typical pharmacokinetic model including 3 compartments is shown in Figure 1. Here, V1 represents the central blood compartment, the other 2

compartments named V2 and V3 are considered as an additional fast and another slow metabolizing compartment. Therefore, the incoming intravenous drug (i.v.) will go with the reaction

coefficient k10 out of the body (elimination) and with e.g. k13 from V1 to V3 and k31 from V3 back to V1, respectively. The clearance of the central compartment is described as V1 * k10 and

the concentration in compartment V3 is represented by the value V3 = V1 * k13/k31. Thus, the clearance 2 is V2 * K21. For the administration of propofol we used the Marsh data set14 with a

constant target concentration of 3 µg/ml in compartment V1. The corresponding values of V1 and the reaction coefficients are shown in Table 1. Here, following to the Marsh model, V1 is

calculated with the weight of the patient multiplied with 0.228 (Table 1). The major disadvantage of TCI is that the concentrations are only calculated and may have a deviation of about 25%3

in healthy patients. The remifentanil target concentration (Minto, plasma mode)15 was adjusted to clinical needs. PHARMACOKINETIC MODELING Plotting the exhaled propofol concentration versus

the calculated propofol plasma concentration revealed a hysteresis loop (see below). Therefore, it is necessary to include the measured propofol concentration into a pharmacokinetic model.

Two different approaches for kinetic modelling were tried. First the 3-compartment model was extended. We calculated an additional 2-compartment model based on the first compartment of the

Marsh model and a new lung compartment VLung (Fig. 2). For the relationship between exhaled propofol concentration and the respective propofol lung concentration values a polynomial second

order was used. VLung, ClLung and the parameters of the polynomial second order were estimated using nonlinear regression with ordinary least squares. The computations were performed on a

spreadsheet using the Excel 2010 software program (Microsoft). The parameters were optimized to maximise R2 using the Solver tool within Excel. The second approach was to calculate a time

delay of the plasma concentration dependent to the measurements of exhaled propofol concentrations as a first order model (Fig. 3). The computation was performed in the same way as described

above. Concentrations measured with the IMS are given as intensities in volt. Usually concentrations in this range are given as parts per billion [ppb]. The transfer from volt to ppb was

performed with a calibration curve. Therefore, the modelling of both approaches was done two times for volt and ppb. A difference occurs due to the non-linear response of the ion mobility

spectrometer within the calibration curve. RESULTS The P-IMS was tested in patients under clinical conditions in the operation room. To demonstrate the mathematical PK/PD modeling approaches

data from one patient were used. The duration of this measurement was 346 min. We were able to perform one measurement each minute. There was no technical failure of the P-IMS hardware or

software. During induction of anaesthesia the exhaled propofol concentration increased with a time delay compared to the TCI plasma concentration. During the maintenance of anaesthesia, the

exhaled propofol concentration increased continuously. The propofol TCI target plasma concentration was set stable at 3 µg/ml. At the end of the surgical procedure the propofol TCI

administration was stopped. The exhaled propofol concentration decreased with a small time delay (Fig. 4). PK-MODELING Plotting the propofol breath concentration peak intensity [volt] a) or

[ppb] b) versus calculated propofol plasma concentration revealed a hysteresis loop (Fig. 5). Figure 5 indicates that a direct correlation analysis between plasma concentrations and exhaled

concentrations is not useful. These calculations lead to poor R2 values (R2 = 0,32 [volt]; R2 = 0,41 [ppb]). PROPOFOL LUNG COMPARTMENT CONCENTRATION The hysteresis loop collapsed by

introduction of the propofol lung compartment concentration or a time delay of the propofol plasma concentration (Fig. 6/Fig. 7). Using the measured breath concentration in ppb the propofol

lung compartment of this individual patient could be described by a volume of 17 L and a clearance of 3,75 L/min. The rate constants were k1L = 0,209 min−1 and kL1 = 0,138 min−1. Using these

parameters for calculation the lung compartment concentration yielded into a correlation coefficient of R2 = 0.99 (Fig. 6b). The polynomial second order is given by: y = −5.9*x2 + 9.23*x +

0, where y is the lung compartment concentration and x the propofol breath concentration. The correlation value is lower using the original intensity values given in volt (R2 = 0.87)(Fig.

6a). y = −12.6*x2 + 15.57*x + 0, where y is the lung compartment concentration and x the propofol peak intensity. TIME DELAY OF THE PROPOFOL PLASMA CONCENTRATION The time delay

pharmacokinetic modeling approach results into a lower correlation coefficient R2 = 0.96 than using an additional compartment for describing the lung propofol concentration (Fig. 7). The

correlation between the model and measurements in ppb is R2 = 0.96 (Fig. 7b). y = −4.2*x2 + 7.14*x + 0, where y is the lung compartment concentration and x the propofol concentration. The

propofol lung plasma time delay concentration of this individual patient was calculated with a first- order rate constant determining the equilibration between plasma and lung concentration

ke0lung = 0.27 min−1. The correlation value is lower using the original intensity values given as peak height measured in volt (R2 = 0.82) (Fig. 7a). y = −7.7*x2 + 9.64*x + 0, where y is the

lung compartment concentration and x the propofol peak intensity. DISCUSSION In this manuscript two different pharmacological models are presented for the description of the pharmacokinetic

of exhaled drug concentrations. The calculations were exemplarily performed for propofol, an intravenous anaesthetic widely used in clinical practice. The exhaled propofol concentration was

measured with a modified MCC/IMS (P-IMS). Under clinical conditions it is not possible to measure the propofol blood concentration online. Therefore, computer-assisted infusion pumps

(Target controlled infusion (TCI)) were developed to calculate the propofol blood concentration based on the demographic patient data and the dosage12. A 3-compartment pharmacokinetic model

is used for the calculation of the blood concentration. This blood or plasma concentration is given in the first compartment V1. Our first PK modeling approach is to extend this

3-compartment model for another 2-compartment model. The first compartment V1 is used parallel for both models. The second compartment of the 2-compartment model represents the lung

compartment. The lung compartment has a volume (VLung). The volume is given in liters (L). The value is a virtual volume of distribution and not physiologically. The second parameter is the

clearance of the compartment given in L/min (ClLung). Both values are used to calculate rate constants for metabolism and elimination. We have named these constants as k1L and kL1. kL1 is

the deviation of the volume of the lung compartment and clearance of the lung compartment. k1L is required to balance the drug concentration between the lung compartment and the blood

compartment. This PK approach has to be used if the drug is metabolized by the lung or if the drug accumulates in the lung. If there a metabolism of the drug in the lung the clearance value

is positive. The clearance value is negative, if an accumulation is present. For propofol there are some publications from animal studies, hypothesizing that propofol is metabolized by the

lung16. Our second approach could be used, if there is only a time delay between changes of the drug concentration and exhaled concentrations. This PK model excludes changes of the

concentration by the lung itself. The equilibration between plasma and lung concentration is described by a first-order rate constant (ke0). The ke0 value describes the time delay between

changes of the blood concentration of anaesthetics and their effect at the brain measured with the EEG17. The transition of anaesthetics across the blood–brain barrier needs a certain time.

The effects of anaesthetics on the brain can be measured with an EEG monitor18. Then this method was transferred to describe the time delay between changes of the measured end-tidal

concentration of volatile anaesthetics and the EEG effect19. Equilibration between end-tidal and brain concentrations of volatile anaesthetics is reached after a time delay that is

substance-specific and called hysteresis, i.e. the delay between the maximum plasma concentration and the maximum EEG effect. In PK/PD models this hysteresis is considered by inclusion of a

fictitious compartment, the so called “effect compartment”. We used this mathematical procedure now to describe a time delay between changes of the drug blood concentrations and the exhaled

concentrations. To distinguish between the “traditional” ke0 value10 and the new approach we introduced the term ke0lung. In generally, the higher the value of ke0lung, the shorter the time

of equilibration between exhaled and blood concentration. In our sample calculation for propofol both methods were suitable to describe the pharmacokinetic of the exhaled propofol

concentration. We used a polynomial of second order as a function for the PK model. For other drugs or biomarkers a linear correlation analysis could be sufficient. In other cases it could

be necessary to choose a polynomial of a higher degree or a different mathematical model. The calculations were performed for one individual patient. For one patient PK modeling could be

done within Excel using the solver tool to optimize the correlation between the pharmacology model and measurements. For further analysis data of several patients in one step a Bayesian

probability calculation is necessary19. The presented PK modeling methods are suitable for the continuous application of a drug. In principle they could also be used for a single bolus

application. The pharmacological principles demonstrated for propofol in this manuscript could be transferred to other medications. For propofol, further studies including measured propofol

blood concentrations are necessary to build a PK model, which could be transferred into clinical practice. Online measurement of drug concentrations in patient's breath is a new

promising approach for individualized dosage of medications. Unfortunately there is no direct correlation between exhaled and blood concentration of the drug. Therefore pharmacokinetic

modelling is necessary for research and clinical practice. REFERENCES * Barakat, A. R., Sutcliffe, N. & Schwab, M. Effect site concentration during propofol TCI sedation: a comparison of

sedation score with two pharmacokinetic models. Anaesthesia. 62, 661–666 (2007). Article  CAS  Google Scholar  * Eissing, T. et al. A computational systems biology software platform for

multiscale modeling and simulation: integrating whole-body physiology, disease biology and molecular reaction networks. Front Physiol. 24, 2–4 (2011). Google Scholar  * Glen, J. B. &

Servin, F. Evaluation of the predictive performance of four pharmacokinetic models for propofol. Br J Anaesth. 102, 626–632 (2009). Article  CAS  Google Scholar  * Tszyrsznic, W. et al. Two

rapid ultra performance liquid chromatography/tandem mass spectrometry (UPLC/MS/MS) methods with common sample pretreatment for therapeutic drug monitoring of immunosuppressants compared to

immunoassay. J Chromatogr B Analyt Technol Biomed Life Sci. 928, 9–15 (2013). Article  CAS  Google Scholar  * Berchtold, C., Bosilkovska, M., Daali, Y., Walder, B. & Zenobi, R. Real-time

monitoring of exhaled drugs by mass spectrometry. Mass Spectrom 22, 10.1002/mas.21393. (2013). * Beck, O., Sandqvist, S., Eriksen, P., Franck, J. & Palmskog, G. Determination of

methadone in exhaled breath condensate by liquid chromatography- tandem mass spectrometry. J Anal Toxicol 35, 129–133 (2011). Article  CAS  Google Scholar  * Perl, T. et al. Determination of

serum propofol concentrations by breath analysis using ion mobility spectrometry. Br J Anaesth 103, 822–827 (2009). Article  CAS  Google Scholar  * Gamez, G. et al. Real-time, in vivo

monitoring and pharmacokinetics of valproic acid via a novel biomarker in exhaled breath. Chem Commun 47, 4884–4886 (2011). Article  CAS  Google Scholar  * Lu, C. C. et al. Pharmacokinetics

of sevoflurane uptake into the brain and body. Pharmacology. 69, 132–137 (2003). Article  CAS  Google Scholar  * Kreuer, S., Bruhn, J., Wilhelm, W. & Bouillon, T. Pharmacokinetic

pharmacodynamic models for inhaled anaesthetics. Anaesthesist. 56, 538–556 (2007). Article  CAS  Google Scholar  * Kreuder, A. E. et al. Characterization of propofol in human breath of

patients undergoing anesthesia. Int. J. Ion Mobil. Spec. 14, 167–175 (2011). Article  CAS  Google Scholar  * Schraag, S., Kreuer, S., Bruhn, J., Frenkel, C. & Albrecht, S.

Target-controlled infusion (TCI) - a concept with a future?: state-of-the-art, treatment recommendations and a look into the future. Anaesthesist. 57, 223–230 (2008). Article  CAS  Google

Scholar  * Buchinger, H. et al. Minimal retarded Propofol signals in human breath using ion mobility spectrometry. Int. J. Ion Mobil. Spec. 16, 185–190 (2013). Article  Google Scholar  *

Marsh, B., White, M., Morton, N. & Kenny, G. N. Pharmacokinetic model driven infusion of propofol in children. Br J Anaesth. 67, 41–48 (1991). Article  CAS  Google Scholar  * Minto, C.

F., Schnider, T. W. & Shafer, S. L. Pharmacokinetics and pharmacodynamics of remifentanil. II. Model application. Anesthesiology. 86, 24–33 (1997). Article  CAS  Google Scholar  * Matot,

I., Neely, C. F., Katz, R. Y. & Neufeld, G. R. Pulmonary uptake of propofol in cats. Effect of fentanyl and halothane. Anesthesiology. 78, 1157–1165 (1993). Article  CAS  Google Scholar

  * Kreuer, S., Wilhelm, W., Grundmann, U., Larsen, R. & Bruhn, J. Narcotrend index versus bispectral index as electroencephalogram measures of anesthetic drug effect during propofol

anesthesia. Anesth Analg. 98, 692–697 (2004). Article  CAS  Google Scholar  * Ellerkmann, R. K., Soehle, M. & Kreuer, S. Brain monitoring revisited: what is it all about? Best Pract Res

Clin Anaesthesiol. 27, 225–233 (2013). Article  Google Scholar  * Kreuer, S. et al. Comparative pharmacodynamic modeling of desflurane, sevoflurane and isoflurane. J Clin Monit Comput. 23,

299–305 (2009). Article  Google Scholar  Download references ACKNOWLEDGEMENTS A.H. is grateful for financial aid provided by the International Max Planck Research School, Saarbrücken,

Germany. Part of the work of this paper has been supported by the Deutsche Forschungsgemeinschaft (DFG) within the Collaborative Research Center (Sonderforschungsbereich) SFB 876 Providing

Information by Resource-Constrained Analysis, project TB1 Resource-Constrained Analysis of Spectrometry Data (JIBB). The clinical study has been supported by Fresenius Kabi (Bad Homburg,

Germany). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Anaesthesiology, Intensive Care and Pain Therapy, Saarland University Medical Center and Saarland University Faculty of

Medicine, 66482 Homburg/Saar, Germany S. Kreuer, T. Fink & Th. Volk * Max Planck Institute for Informatics, Research Group on Computational Systems Biology, Campus E2.1, R. 203, 66123,

Saarbrücken, Germany A. Hauschild * Reutlingen University, Faculty Applied Chemistry, Alteburgstrasse 150, 72762, Reutlingen, Germany J. I. Baumbach * B&S Analytik, BioMedicalCenter

Dortmund, Otto-Hahn-Str. 15, 44227, Dortmund, Germany S. Maddula Authors * S. Kreuer View author publications You can also search for this author inPubMed Google Scholar * A. Hauschild View

author publications You can also search for this author inPubMed Google Scholar * T. Fink View author publications You can also search for this author inPubMed Google Scholar * J. I.

Baumbach View author publications You can also search for this author inPubMed Google Scholar * S. Maddula View author publications You can also search for this author inPubMed Google

Scholar * Th. Volk View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS S.K., T.V. and J.I.B. wrote the manuscript. S.K. developed the

pharmacokinetic models. S.K., S.M., A.H. prepared the excel sheet for the calculation. T.F. performed the patient measurement and prepared figures 1–3. All authors reviewed the manuscript.

ETHICS DECLARATIONS COMPETING INTERESTS Patent applications for the measurement of exhaled propofol (J.I.B.; S.K.; T.V.). Related to the present pharmacokinetic models there are no financial

interests. RIGHTS AND PERMISSIONS This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included

in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain

permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS

ARTICLE CITE THIS ARTICLE Kreuer, S., Hauschild, A., Fink, T. _et al._ Two different approaches for pharmacokinetic modeling of exhaled drug concentrations. _Sci Rep_ 4, 5423 (2014).

https://doi.org/10.1038/srep05423 Download citation * Received: 24 April 2014 * Accepted: 04 June 2014 * Published: 24 June 2014 * DOI: https://doi.org/10.1038/srep05423 SHARE THIS ARTICLE

Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided

by the Springer Nature SharedIt content-sharing initiative