Insulator–metal transition in CrSiTe3 triggered by structural distortion under pressure

Download PDF Article Open access Published: 07 April 2023 Insulator–metal transition in CrSiTe3 triggered by structural distortion under pressure J. L. Musfeldt  ORCID:

orcid.org/0000-0002-6241-823X1,2, D. G. Mandrus  ORCID: orcid.org/0000-0003-3616-71043,4 & Z. Liu  ORCID: orcid.org/0000-0003-2617-70775  npj 2D Materials and Applications volume 7, Article 

number: 28 (2023) Cite this article

2879 Accesses

3 Citations

1 Altmetric

Metrics details

van der Waals solids are well known to host remarkable phase diagrams with competing phases, unusual energy transfer processes, and elusive states of matter. Among this class of materials,

chalcogenides have emerged as the most flexible and relevant platforms for unraveling charge–structure–function relationships. In order to explore the properties of complex chalcogenides

under external stimuli, we measured the far infrared spectroscopic response of CrSiTe3 under extreme pressure–temperature conditions. Analysis of the 368 cm−1 Si–Te stretching mode and the

manner in which it is screened by the closure of the indirect gap reveals that the insulator–metal transition takes place immediately after the structural phase transition—once the mixed

phase aspect of the lattice distortion is resolved. At the same time, the two-phase region associated with the structural transition widens with decreasing temperature, and the slope of the

insulator–metal transition under pressure is consistent with increasing entropy. These trends completely revise the character of the temperature–pressure phase diagram as well as the

relationship between the structural and insulator–metal transitions, leading to a critical nexus of activity that may hide a quantum critical point and allow superconductivity to emerge.

Similar content being viewed by others Symmetry progression and possible polar metallicity in NiPS3 under pressure Article Open access 09 June 2022 Superatomic solid solutions Article 26

April 2021 Phonon mixing in the charge density wave state of ScV6Sn6 Article Open access 13 October 2023 Introduction

Complex chalcogenides are exceptionally responsive to external stimuli. Under compression, systems like CrSiTe3, FePS3, MnPS3, and CrGeTe3 host layer sliding, insulator–metal transitions,

magnetic dimensionality crossovers, piezochromism, the possibility of orbital-selective Mott and polar metal states, and

superconductivity1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22. The 33 K ferromagnet CrSiTe3 has earned widespread recognition for remarkable properties in both single crystal and

monolayer form23,24,25,26,27. The discovery of pressure-induced superconductivity above 7.5 GPa and below 4.2 K is one of these exciting developments27. Establishing the local lattice

distortions and the precise relationship between the structural and insulator–metal transitions is crucial to unraveling how superconductivity develops and distinguishing between

conventional vs. unconventional mechanisms in this class of materials. At the same time, CrSiTe3 is a layered van der Waals material that has attracted extraordinary attention for the

demonstration of single-layer ferromagnetism and current-driven control of the spin state26,28,29,30,31,32,33,34. Whether superconductivity arises in the ultrathin limit is currently

unexplored, although the fact that the Curie temperature TC rises with decreasing layer number as well as under strain and pressure30,31,34 suggests that the superconducting transition

temperature might do so as well35,36. Further developing the phase diagram and resolving the connection between the structural and insulator–metal transitions as well as the intersection of

competing phases is a significant step toward evaluating such a relationship.

In order to explore these themes in a complex chalcogenide, we combined synchrotron-based infrared spectroscopy and diamond anvil cell techniques to measure the far-infrared response of

CrSiTe3 under extreme pressure–temperature conditions. Because closing an indirect gap screens the phonons much less effectively than closing a direct gap, we can follow the evolution of the

phonons into the metallic state. The 2Eu symmetry Si–Te stretching mode at 368 cm−1—noteworthy for engaging in spin-phonon coupling across the magnetic ordering transition23—is particularly

informative in this regard. This vibrational mode hardens strongly on approach to the pressure-driven structural transition, broadens and develops weak doublet character in the mixed-phase

region, and rides on top of a gradually increasing electronic background as the indirect gap begins to close. In the end, the insulator–metal transition is swift and sharp. What

differentiates our work from previous results is the finding that the first-order structural phase transition in CrSiTe3 is triggered before (but in close proximity to) the insulator–metal

transition. The latter is set in motion almost immediately afterward. With decreasing temperature, the two-phase region associated with the structural transition broadens, and the

insulator–metal transition shifts to slightly higher pressure, indicative of a positive entropy change. Our findings run counter to previous results27 and completely revise the entire

character of the temperature–pressure (T–P) phase diagram for this compound. These trends also open the possibility that the juxtaposition of events both hides a quantum critical point and

lays the foundation for superconductivity.

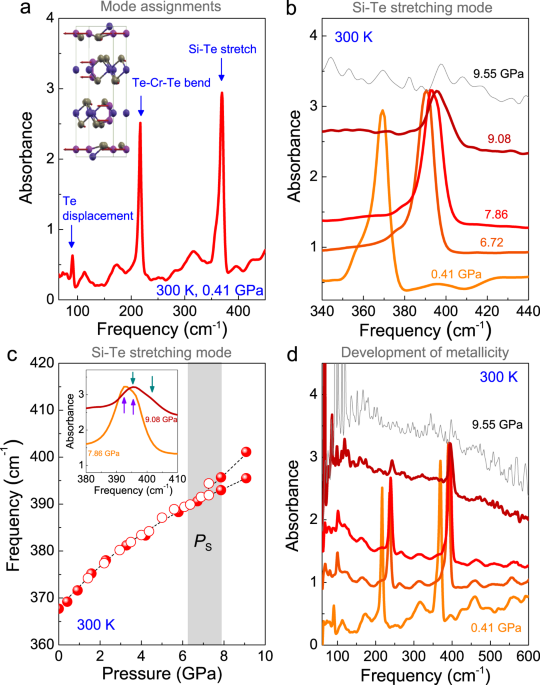
Figure 1a displays the infrared response of CrSiTe3 at ambient conditions inside the diamond anvil cell. Three infrared-active vibrational modes are observed. We assign the peak near 90 cm−1

as an Au symmetry Te displacement mode, the feature near 215 cm−1 as an 1Eu symmetry Te–Cr–Te bending mode, and the peak at 368 cm−1 as a 2Eu symmetry Si–Te stretching mode. All of these

features harden significantly under pressure. In order to understand the local lattice distortions associated with the structural phase transition, we track the frequency shifts and

splittings of these phonons as a function of pressure. The behavior of the Si–Te stretching mode determines the location of the structural phase transition. We find that weak doublet

character signals a mixed phase region that persists over a broad pressure range [Fig. 1c]. Oscillator fits of the Si–Te phonon reveal where the process begins and ends. The insulator–metal

transition is different. Due to the superior stability and brightness of the synchrotron source, we can measure absorption very close to the metallic transition—even though the signal is

low—and we can follow the entire transition into the metallic phase because CrSiTe3 is a bad metal with an indirect gap. As an additional check, we monitor the emerging metallicity with

complementary reflectance spectroscopy. Both techniques provide similar estimates of the critical pressure for the insulator–metal transition.

pressure.

a Infrared spectrum of CrSiTe3 inside the diamond anvil cell at 300 K. Based upon an \(R\bar{3}\) space group, this van der Waals material hosts three infrared-active phonon modes. The 368

cm−1 Si–Te stretching mode is strongly coupled to the 33 K ferromagnetic ordering transition23. Inset: calculated displacement pattern for the Si–Te stretching mode at 368 cm−1 reproduced

from ref. 23. This displacement modulates the Te centers in the 90∘ Cr–Te–Cr superexchange pathway. b Close-up view of the Si–Te stretching mode showing the development of the first-order

structural phase transition, the rising absorption background, and metallicity. c Frequency vs. pressure plot of the Si–Te stretching mode at room temperature. The closed and open symbols

correspond to two different runs. The mixed phase region associated with the structural phase transition is indicated in gray. Inset: close-up view of the Si–Te stretch showing the

development of doublet character due to the presence of two coexisting phases. d Spectral evidence for the insulator–metal transition due to closure of the indirect gap near 9.55 GPa

(indicated in gray). The spectra are on an absolute scale; they are not shifted in any way. Complementary reflectance data are shown in the Supporting information.

of pressure-driven transitions in CrSiTe3 at room temperature

The behavior of the 368 cm−1 Si–Te stretching mode is particularly revealing [Fig. 1b, c]. In addition to hardening strongly under pressure (∂ω/∂P = 3.4 cm−1/GPa at 300 K), the Si–Te stretch

broadens considerably between approximately 6 and 8 GPa and displays a poorly resolved doublet structure. Oscillator fits of these features are shown in the Supporting information. This

broadening and eventual peak separation could be a signature of (i) weak symmetry breaking or (ii) a mixed phase regime. There are two pieces of evidence that point toward the latter

scenario. First, the character of the frequency vs. pressure plot in Fig. 1c is consistent with phase coexistence. Second, the x-ray diffraction data of Cai et al. provide clear evidence for

a sluggish structural phase transition between \(R\bar{3}\) and a high-pressure phase over the same range27. We therefore attribute the broadening and subsequent weak doublet character of

the Si–Te stretching mode to the simultaneous presence of two slightly different structural phases between approximately 6 and 8 GPa. CrSiTe3 therefore goes from \(R\bar{3}\,\to\) a two

phase region that is a combination of \(R\bar{3}\) + the high-pressure phase → a high-pressure phase that is slightly different from \(R\bar{3}\). The mixed-phase regime is relatively narrow

at room temperature, and the subsequent high-pressure structure does not last long in isolation. In fact, the appearance of this phase almost immediately triggers the insulator–metal

transition. Based upon room temperature x-ray diffraction27, the structure of the high-pressure and metallic phases are probably the same. A similar scenario in terms of transition primacy

plays out in FePS316.

Metallicity in CrSiTe3 develops gradually at room temperature. The absorption background rises with increasing pressure, and the phonons rise partially screened above it until the 0.4 eV

indirect gap closes, completely obscuring the phonons [Fig. 1d]. This definition of the onset to the insulator–metal transition is consistent with the gradual maturation of metallicity in

the relectance spectra as well. Tracking the development of metallicity in this manner is a much better way to determine the location of the insulator–metal transition than from an

inflection point or “hump” in the resisitivity27. The “hump method” might work for a direct gap material, but the closure of the indirect gap in CrSiTe3 is more subtle. In our hands, the

indirect gap is fully closed, and metallicity is established at 9.5 GPa. We reiterate that it is very clear that the 0.4 eV indirect gap is closing—not the 1.2 eV direct gap23, because the

latter does not move into our frequency window. This makes the system a bad metal. Closure of a direct gap would likely be sharp and strong. There would be no chance of seeing phonons after

metallicity sets in due to screening effects. Indirect gap closure, on the other hand, is a very favorable situation, giving a beautiful view of the structural transition and gradual

evolution of metallicity.

CrSiTe3 hosts a similar pattern of phonons at lower temperatures, and the three infrared-active vibrational modes get sharper due to lifetime effects. The two-phase region (consisting of

\(R\bar{3}\) and a higher pressure phase with slightly different structure) broadens considerably and becomes more sluggish with decreasing temperature. Metallicity appears only after the

structural phase transition is complete—typically near 9.5 GPa. At 100 K, the insulator–metal transition is above 10 GPa, indicating that the phase boundary is moving outward. The trend is

even stronger at 50 K [Fig. 2], and the mixed phase persists over a wider pressure range than before. Even so, the structural phase transition is always complete before the insulator–metal

transition takes place and once it is resolved, metallicity arises almost immediately. Each step is an independent process, and the sequence is invariably the same: \(R\bar{3}\,\) → mixed

phases → high pressure structural phase → insulator–metal transition. This progression is exactly opposite of what is reported in ref. 27.

extreme pressure–temperature conditions.

a Close-up view of the infrared-active Si–Te stretching mode showing the development of the first-order structural phase transition. The two-phase region becomes more sluggish with

decreasing temperature. Oscillator fits are available in the Supporting information. b Spectral evidence for the insulator–metal transition due to closure of the indirect gap. The background

is rising, and the phonons rise incompletely screened on top of the metallic background until the indirect gap closes and the signature of the phonons disappears due to screening by the

Drude (indicated in gray). These spectra are on an absolute scale; they are not shifted in any way.

The space group in the narrow high-pressure region between the structural phase transition and the insulator–metal transition is also of interest. Unfortunately, the phonons are heavily

screened in this bad metal region, making it difficult to analyze symmetry breaking and carry out a subgroup analysis20,22. We can, however, state that the high-pressure vibrational

properties of CrSiTe3 above the two-phase region are inconsistent with the R3 space group that has been proposed for CrGeTe37 because the infrared spectra of CrSiTe3 provide no evidence for

a loss of the inversion center which is expected for a transition to a polar space group. Clearly, more effort is needed to reveal the symmetry and properties of CrSiTe3 above the structural

phase transition.

Figure 3 displays the T–P phase diagram of CrSiTe3, created by bringing together spectroscopic information about the structural and insulator–metal transitions described above with selected

data on the pressure dependence of the Curie and superconducting transition temperatures from ref. 27. The overall character of the phase diagram is quite different from the previous

report27 especially in terms of the sequence of the structural and insulator–metal phase transitions and the shape of the phase boundaries. In our hands, the structural transition is

initiated and fully complete before the insulator–metal transition takes place, and metallicity is due to the closure of the indirect gap. We know that the direct gap is still open at 10 GPa

because we do not see it come into our spectral range at these pressures. Closure of the direct gap takes place at higher pressure.

Temperature–pressure phase diagram summarizing the structural, magnetic, and electronic properties of CrSiTe3. The beginning and end of the structural phase transition as well as the

position of the insulator–metal transition are determined from the spectroscopic results discussed here. The Curie temperature and the superconducting transition temperature (×5) as a

function of pressure are from ref. 27.

As indicated on the T–P phase diagram, the insulator–metal phase boundary occurs after the structural phase transition—not before—and it moves to higher pressure with decreasing temperature.

Therefore the slope of ∂T/∂P is negative rather than positive as previously supposed27. From a thermodynamic point of view, this means that changes in volume and entropy have opposite

signs. Since the volume change ΔV is likely ≤ 0 under compression, the change in entropy ΔS is probably ≥ 037. In other words, entropy increases across the insulator–metal transition.

Similar trends are observed in 1T-TiSe238. By contrast, the two-phase region of the structural phase transition broadens with decreasing temperature. That the mixed phase region is larger at

low temperatures might be due to non-hydrostaticity, but it is more likely a consequence of the first-order transition exhibiting a wider hysteresis. Even so, the structural phase

transition is much more involved in the development of superconductivity than previously believed. At the lowest temperatures that we could reach while still increasing pressure in situ,

both the structural and insulator–metal transitions occur in quick succession and seem to be in very close proximity to a number of competing states including superconductivity. This

intersection of states suggests that a quantum critical point may reside in the vicinity. While we can not say anything specific about the superconducting state in CrSiTe3, we now better

understand the sequence of events leading up to superconductivity. In fact, it may turn out that the insulator–metal transition directly triggers superconductivity at low

temperature.

Thus far, we measured the far infrared response of CrSiTe3 under extreme pressure–temperature conditions in order to reveal how pressure controls the interplay between the structural phase

transition, the insulator–metal transition, ferromagnetism, and superconductivity in a complex chalcogenide. We find that the insulator–metal transition is triggered by the structural phase

transition almost immediately—once the sluggish mixed-phase region is eliminated. Furthermore, the structural transition widens with decreasing temperature, and the slope of the

insulator–metal transition is consistent with increasing entropy. These trends change completely the character of the T–P phase diagram and lead to a critical nexus of activity that may hide

a quantum critical point and allow superconductivity to emerge at low temperature. Extension of the T–P phase diagram toward the few- and single-sheet limit is highly desirable. There is

already evidence in other systems such as FeSe and TaS2 that the superconducting transition temperature TC increases in the ultrathin limit35,36. Here, it is important to use a technique

that can accurately identify closure of the indirect gap. As we discuss, dc conductivity is not very good for establishing the insulator–metal transition in CrSiTe3, but it should be ideal

for identifying the superconducting transition. Infrared techniques by contrast are superb for tracking the structural and insulator–metal transitions in CrSiTe3 but will probably be less

successful following the transition to the superconducting state. In principle, infrared spectroscopy can see the gap open (if the system is s-wave), but it will be challenging to see a

superconducting gap develop inside a diamond anvil cell at low temperature and in the ultrathin limit. Techniques based upon relative slope changes in the reflectance may be successful if

electron-phonon processes are relevant39. Beyond unraveling the sequence of transitions that trigger superconductivity in CrSiTe3, the ability to control complex chalcogenides under pressure

will advance the science base and support the development of high-performance photoresponsive devices and efficient hydrogen storage40,41.

anvil cell

High-quality CrSiTe3 single crystals were grown via flux techniques as described previously23. A small, well-shaped piece of the crystal was selected and loaded into a suitably-chosen

diamond anvil cell with a hydrocarbon grease (petroleum jelly) pressure medium to ensure quasi-hydrostatic pressure conditions and an annealed ruby ball to determine pressure via

fluorescence42. The synthetic type IIas diamonds in the symmetric diamond anvil cell had 500 μm culets, and we employed a 47 μm thick pre-indented stainless steel gasket with a 200 μm hole

diameter. Care was taken to optimize optical density in order to reveal the features of interest.

Taking advantage of the stable, high-brightness beam, synchrotron-based infrared spectroscopy (60-680 cm−1; 4 cm−1 resolution; both transmittance and reflectance geometries) was performed

using the 22-IR-1 beamline at the National Synchrotron Light Source II at Brookhaven National Laboratory. Absorbance is calculated as α(ω) = -ln(\({{{\mathcal{T}}}}\)(ω)), where

\({{{\mathcal{T}}}}\)(ω) is the measured transmittance. The pressure was increased between 0 and 11 GPa—first at room temperature and then at several lower temperatures using a custom-built

cryostat that accomodates the diamond anvil cell and supports in situ compression measurements. For the low-temperature experiments, one ruby ball was positioned inside the sample chamber

while another was placed on the diamond backplate as a temperature reference42. We also monitored the shape of the ruby fluorescence spectrum to ensure that the sample remained in a

quasi-hydrostatic environment. Although an open flow system, this cryostat is limited to work above approximately 50 K in order to control the step size during isothermal compression of the

diamond anvil cell. Our protocol for determining the position of each phase transition was developed at room temperature (as described in the Supporting information) and then extended to low

temperature. The phase transitions are fully reversible upon the release of pressure at each temperature. Further, recompression of the same crystal and then release gives the same results,

so we can be confident that crystal quality remains high under these extreme pressure–temperature conditions.

Data are available from the corresponding author upon reasonable request.

References Zallen, R. Effect of pressure on optical properties of crystalline As2S3. High Pres. Res. 24, 117 (2004).

Article  CAS  Google Scholar 

Wang, Y. et al. Pressure-driven cooperative spin-crossover, large-volume collapse, and semiconductor-to-metal transition in manganese(II) honeycomb lattices. J. Am. Chem. Soc. 138, 15751

(2016).

Article  CAS  Google Scholar 

Haines, C. et al. Pressure-induced electronic and structural phase evolution in the van der Waals compound FePS3. Phys. Rev. Lett. 121, 266801 (2018).

Article  CAS  Google Scholar 

Wang, Y. et al. Emergent superconductivity in an iron-based honeycomb lattice initiated by pressure-driven spin-crossover. Nat. Commun. 9, 1914 (2018).

Article  Google Scholar 

Coak, M. J. et al. Isostructural Mott transition in 2D honeycomb antiferromagnet V0.9PS3. npj Quant. Mater. 4, 38 (2019).

Article  Google Scholar 

Zheng, Y., Jiang, X. X., Xue, X. X., Dai, J. & Feng, Y. Ab initio study of pressure-driven phase transition in FePS3 and FePSe3. Phys. Rev. B 100, 174102 (2019).

Article  CAS  Google Scholar 

Yu, Z. et al. Pressure-induced structural phase transition and a special amorphization phase of two-dimensional ferromagnetic semiconductor Cr2Ge2Te6. J. Phys. Chem. C 123, 13885–13891

(2019).

Article  CAS  Google Scholar 

Kim, H. S., Haule, K. & Vanderbilt, D. Mott metal-insulator transitions in pressurized layered trichalcogenides. Phys. Rev. Lett. 123, 236401 (2019).

Article  CAS  Google Scholar 

Wang, X. et al. Current-driven magnetization switching in a van der Waals ferromagnet Fe3GeTe2. Sci. Adv. 5, eaaw8904 (2019).

Article  CAS  Google Scholar 

Susilo, R. A. et al. Band gap crossover and insulator-metal transition in the compressed layered CrPS4. npj Quant. Mater. 5, 58 (2020).

Article  CAS  Google Scholar 

Coak, M. J. et al. Tuning dimensionality in van-der-Waals antiferromagnetic Mott insulators TMPS3. J. Phys.: Condens. Matter 32, 124003 (2020).

CAS  Google Scholar 

Harms, N. C. et al. Piezochromism in the magnetic chalcogenide MnPS3. npj Quant. Mater. 5, 56 (2020).

Article  CAS  Google Scholar 

Kang, S. et al. Coherent many-body exciton in van der Waals antiferromagnet NiPS3. Nature 583, 785–789 (2020).

Article  CAS  Google Scholar 

Wildes, A. R. et al. High field magnetization of FePS3. Phys. Rev. B 101, 024415 (2020).

Article  CAS  Google Scholar 

Ma, X. et al. Dimensional crossover tuned by pressure in the layered magnetic NiPS3. Sci. China Phys. Mech. Astron. 64, 297011 (2021).

Article  CAS  Google Scholar 

Coak, M. J. et al. Emergent magnetic phases in pressure-tuned van der Waals antiferromagnet FePS3. Phys. Rev. X 11, 011024 (2021).

CAS  Google Scholar 

Kim, M., Kim, H.-S., Haule, K. & Vanderbilt, D. Orbital-selective Mott phase and non-Fermi liquid in FePS3. Phys. Rev. B 105, L041108 (2022).

Article  CAS  Google Scholar 

Zhu, F. F. et al. Topological magnon insulators in two-dimensional van der Waals ferromagnets CrSiT3 and CrGeTe3: Toward intrinsic gap-tunability. Sci. Adv. 7, eabi7532 (2021).

Article  CAS  Google Scholar 

Mai, T. T. et al. Magnon-phonon hybridization in 2D antiferromagnet MnPSe3. Sci. Adv. 7, eabj3106 (2021).

Article  CAS  Google Scholar 

Harms, N. C. et al. Symmetry progression and polar metallicity in NiPS3 under pressure. npj 2D Mater. Appl. 6, 40 (2022).

Article  CAS  Google Scholar 

Zhao, H. et al. Mechanical control of physical properties in the van der Waals ferromagnet Cr2Ge2Te6 via application of electric current. Phys. Rev. B 106, L041103 (2022).

Article  CAS  Google Scholar 

Harms, N. C. et al. Metal site substitution and the role of the P-P dimer on symmetry breaking in FePS3 and CrPS4. ACS Appl. Elect. Mater. 4, 3246 (2022).

Article  CAS  Google Scholar 

Casto, L. D. et al. Strong spin-lattice coupling in CrSiTe3. Appl. Phys. Lett. Mater. 3, 041515 (2015).

Google Scholar 

Williams, T. J. et al. Magnetic correlations in the quasi-two-dimensional semiconducting ferromagnet CrSiTe3. Phys. Rev. B 92, 144404 (2015).

Article  Google Scholar 

Liu, B. et al. Critical behavior of the quasi-two-dimensional semiconducting ferromagnet CrSiTe3. Sci. Rep. 6, 33873 (2016).

Article  CAS  Google Scholar 

Gong, C. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265–269 (2017).

Article  CAS  Google Scholar 

Cai, W. et al. Pressure-induced superconductivity and structural transition in ferromagnetic CrSiTe3. Phys. Rev. B 102, 144525 (2020).

Article  CAS  Google Scholar 

Lebegue, S., Bjorkman, T., Klintenberg, M., Nieminen, R. & Eriksson, O. Two-dimensional materials from data filtering and ab initio calculations. Phys. Rev. X 3, 31002 (2013).

CAS  Google Scholar 

Li, X. & Yang, J. CrXTe3 (X = Si, Ge) nanosheets: two dimensional intrinsic ferromagnetic semiconductors. J. Mater. Chem. C 2, 7071–7076 (2014).

Article  CAS  Google Scholar 

Chen, X., Qi, J. & Shi, D. Strain-engineering of magnetic coupling in two-dimensional magnetic semiconductor CrSiTe3: Competition of direct exchange interaction and superexchange

interaction. Phys. Lett. A 379, 60–63 (2015).

Article  CAS  Google Scholar 

Lin, M.-W. et al. Ultrathin nanosheets of CrSiTe3: a semiconducting two-dimensional ferromagnetic material. J. Mater. Chem. C 4, 315–322 (2016).

Article  CAS  Google Scholar 

Zhang, J.-M., Nie, Y.-Z., Xia, Q.-L., Xiong, R. & Guo, G.-H. Electronic structures and magnetic properties of CrSiTe3 single-layer nanoribbons. Phys. Lett. A 383, 2346–2351 (2019).

Article  CAS  Google Scholar 

Ron, A. et al. Unltrafast enhancement of ferromagnetic spin exchange induced by ligand-to-metal charge transfer. Phys. Rev. Lett. 125, 197203 (2020).

Article  CAS  Google Scholar 

Zhang, C. et al. Pressure-enhanced ferromagnetism in layered CrSiTe3 flakes. Nano Lett. 21, 7946–7952 (2021).

Article  CAS  Google Scholar 

Navarro-Moratalla, E. et al. Enhanced superconductivity in atomically thin TaS2. Nature Commun. 7, 11043 (2016).

Article  CAS  Google Scholar 

Shigekawa, K. et al. Dichotomy of superconductivity between monolayer FeS and FeSe. Proc. Nat. Acad. Sci. 116, 24470 (2019).

Article  CAS  Google Scholar 

Smith, K. A. et al. Revealing pressure-driven structural transitions in the hybrid improper ferroelectric Sr3Sn2O7. Phys. Rev. B 104, 064106 (2021).

Article  CAS  Google Scholar 

Kusmartzeva, A. F., Sipos, B., Berger, H., Forró, L. & Tutis, E. Pressure induced superconductivity in pristine 1T-TiSe2. Phys. Rev. Lett. 103, 236401 (2009).

Article  Google Scholar 

Carbotte, J. P., Nicol, E. J. & Timusk, T. Detecting superconducting in the high pressure hydrides and metallic hydrogen from optical properties. Phys. Rev. Lett. 121, 047002 (2018).

Article  CAS  Google Scholar 

Ramos, M. et al. Ultra-broad spectra photo-response in FePS3 air stable devices. npj 2D Mater. Appl. 5, 19 (2021).

Article  CAS  Google Scholar 

Rezaie, A. A., Lee, E., Luong, D., Yapo, J. A. & Fokwa, B. P. T. Abundant active sites on the basal plane and edges of layered van de Waals Fe3GeTe2 for highly efficient hydrogen evolution.

ACS Mater. Lett. 3, 313 (2021).

Article  CAS  Google Scholar 

Mao, H. K., Bell, P. M., Shaner, J. W. & Steinberg, D. J. Specific volume measurements of Cu, Mo, Pd, and Ag and calibration of the ruby R1 fluorescence pressure gauge from 0.06 to 1 Mbar.

J. Appl. Phys. 49, 3276 (1976).

Article  Google Scholar 

Download references

J.L.M. appreciates funding from Physical Behavior of Materials, Basic Energy Sciences, U.S. Department of Energy (Contract number DE-SC00023144). D.M. acknowledges support from the Gordon

and Betty Moore Foundation’s EPiQS Initiative, Grant GBMF9069. Work at the National Synchrotron Light Source II at Brookhaven National Laboratory is funded by the Department of Energy

(DE-AC98-06CH10886). Use of the 22-IR-1 beamline is supported by COMPRES, the Consortium for Materials Properties Research in Earth Sciences, under NSF Cooperative Agreement EAR 1606856 and

CDAC (DE-NA0003975). We thank S. N. Neal, K. Park, and K. A. Smith for useful conversations.

Author informationAuthors and Affiliations Department of Chemistry, University of Tennessee, Knoxville, TN, 37996, USA

J. L. Musfeldt

Department of Physics and Astronomy, University of Tennessee, Knoxville, TN, 37996, USA

J. L. Musfeldt

Department of Materials Science and Engineering, University of Tennessee, Knoxville, TN, 37996, USA

D. G. Mandrus

Materials Science and Technology Division, Oak Ridge National Laboratory, Oak Ridge, TN, 37831, USA

D. G. Mandrus

Department of Physics, University of Illinois Chicago, Chicago, IL, 60607-7059, USA

Z. Liu

AuthorsJ. L. MusfeldtView author publications You can also search for this author inPubMed Google Scholar

D. G. MandrusView author publications You can also search for this author inPubMed Google Scholar

Z. LiuView author publications You can also search for this author inPubMed Google Scholar

J.L.M. designed the study. D.M. grew the crystals. J.L.M. and Z.L. performed the high pressure measurements. J.L.M. analyzed the spectral data and wrote the manuscript. All authors commented

on the text.

Corresponding author Correspondence to J. L. Musfeldt.

The authors declare no competing interests.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

informationRights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or

format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or

other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in

the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the

copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and permissions

About this articleCite this article Musfeldt, J.L., Mandrus, D.G. & Liu, Z. Insulator–metal transition in CrSiTe3 triggered by structural distortion under pressure. npj 2D Mater Appl 7, 28

(2023). https://doi.org/10.1038/s41699-023-00389-x

Download citation

Received: 19 September 2022

Accepted: 10 March 2023

Published: 07 April 2023

DOI: https://doi.org/10.1038/s41699-023-00389-x

Share this article Anyone you share the following link with will be able to read this content:

Get shareable link Sorry, a shareable link is not currently available for this article.

Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by Phonon mixing in the charge density wave state of ScV6Sn6 Yanhong GuEthan T. RitzJanice L. Musfeldt npj Quantum Materials (2023)