Image denoising in acoustic microscopy using block-matching and 4d filter

ABSTRACT Scanning acoustic microscopy (SAM) is a label-free imaging technique used in biomedical imaging, non-destructive testing, and material research to visualize surface and sub-surface

structures. In ultrasonic imaging, noises in images can reduce contrast, edge and texture details, and resolution, negatively impacting post-processing algorithms. To reduce the noises in

the scanned image, we have employed a 4D block-matching (BM4D) filter that can be used to denoise acoustic volumetric signals. BM4D filter utilizes the transform domain filtering technique

with hard thresholding and Wiener filtering stages. The proposed algorithm produces the most suitable denoised output compared to other conventional filtering methods (Gaussian filter,

median filter, and Wiener filter) when applied to noisy images. The output from the BM4D-filtered images was compared to the noise level with different conventional filters. Filtered images

were qualitatively analyzed using metrics such as structural similarity index matrix (SSIM) and peak signal-to-noise ratio (PSNR). The combined qualitative and quantitative analysis

demonstrates that the BM4D technique is the most suitable method for denoising acoustic imaging from the SAM. The proposed block matching filter opens a new avenue in the field of acoustic

or photoacoustic image denoising, particularly in scenarios with poor signal-to-noise ratios. SIMILAR CONTENT BEING VIEWED BY OTHERS A NEW HYBRID IMAGE DENOISING ALGORITHM USING ADAPTIVE AND

MODIFIED DECISION-BASED FILTERS FOR ENHANCED IMAGE QUALITY Article Open access 15 March 2025 ROBUST MEAN SHIFT FILTER FOR MIXED GAUSSIAN AND IMPULSIVE NOISE REDUCTION IN COLOR DIGITAL

IMAGES Article Open access 02 September 2022 WAVELET-BASED INFORMATION THEORY IN QUANTITATIVE ASSESSMENT OF AFM IMAGES’ QUALITY Article Open access 18 February 2024 INTRODUCTION In materials

science to biology, scanning acoustic microscopes (SAM) have been successfully used to image the surface and interior structures and conduct nondestructive evaluations without causing

damage to the material being studied1. In addition to its ability to inspect objects, the SAM is also capable of providing ample and precise quantitative information about the inspected

items. SAM has a range of capabilities, including the non-invasive micro-structural characterization of materials, the characterization of the mechanical properties of piezoelectric

materials on their surfaces and subsurface, structural health monitoring (SHM) of the composite structures, detecting surface defects on polymer circuits, and examining the propagation of

anisotropic phonons2,3,4,5,6,7. The technology of SAM holds significant importance in the fiercely competitive and demanding markets of microelectronics and semiconductor industries. It

plays a vital role in enhancing mold designs for flip-chip packages and is capable of managing the intricacies involved in miniaturized assemblies, such as chip-scale packages and 3D IC

stacks, making it a significant tool in the industry8, 9. The resolution of images generated by SAM at a specific frequency relies on the pixel size or scanning steps in both x and y

directions, along with the acoustic beam's spot size. In ultrasonic imaging, images are generated by collecting signals, and the quality of the resulting images can be greatly affected

by the presence of noise. Images with noise can cause decreased contrast, loss of edge and texture details, and reduced resolution, which can negatively affect post-processing algorithm

performance. Therefore, noise is a critical factor that can contribute to the decline of signal quality in acoustic imaging. Accurate parameter determination from acquired images is reliant

on effective image denoising. The most prevalent and unresolved challenge in ultrasound imaging is the presence of noise from multiple sources, which often leads to significant degradation

of image quality. Consequently, the presence of noise becomes highly limiting in sensitive applications where acoustic contrast plays a crucial role. Due to various factors such as the

environment, electronic noise, transmission cable, and others, images are inevitably subject to noise during acquisition, compression, and transmission, resulting in distortion and loss of

image information. These factors make images vulnerable to the manifestation of random noise during data acquisition. Denoising techniques can be classified into two main categories: spatial

domain methods and transform domain methods. Spatial filters can be further divided into linear and non-linear filters, and they use low-pass filtering on the pixel values of an image since

noise tends to occupy higher regions in the frequency spectrum10. Spatial filters tend to reduce noise to a certain extent, but they often lead to blurring of the image. In contrast, the

transform domain provides various signal processing techniques, such as wavelet decomposition and empirical mode decomposition (EMD), to tackle this problem11. Additionally, methods like

principal component analysis (PCA) and singular value decomposition (SVD) can be used for signal reconstruction and restoration12, 13. Wang et al. utilized a hybrid method that combined wave

packet decomposition and EMD to denoise signals and subsequently classified various engine faults using Support Vector Machine (SVM)14. In a separate study, Fan et al. presented a denoising

algorithm based on principal component analysis (PCA) that was demonstrated using simulated data with varying levels of noise15. Huan et al. introduced a method called C-PCASVD, which

combines principal component analysis (PCA) and singular value decomposition (SVD) to identify the singular values of interference16. This technique enables an optimal balance between the

denoised free induction decay (FID) and the efficiency of noise reduction. In recent times, artificial intelligence (AI) techniques, and more specifically deep learning (DL) approaches, have

demonstrated state-of-the-art performance for many denoising algorithms17,18,19,20,21. Zhang et al. introduced DnCNN, a popular deep convolutional neural network (CNN) for image

denoising22. Other significant contributions in denoising include deep belief networks (DBN)23, stacked auto-encoders (SAE)24, CNN25, and non-local neural networks26. CNN-based architectures

often excel in handling additive white Gaussian noise (AWGN) but may struggle with other types of noise. Additionally, deep learning models for ultrasound image denoising often require

large training datasets, but denoising autoencoders with convolutional layers have shown promising results even with smaller sample sets24. Another approach to de-speckling ultrasound images

is using PCANet27, which has been adapted to include the classical concept of non-local means (NLM)28. The Variational Denoising Network (VDN) is a Bayesian-based denoising model that

integrates noise estimation with image denoising29, 30. However, deep learning-based image denoising faces a significant challenge of requiring a large amount of data, which can be difficult

to obtain in acoustic imaging except for medical sonography. Moreover, the training and validation process typically involves specific images, making it a sample-specific, computationally

expensive, and time-consuming approach. Transform domain filtering methods can be categorized into data-adaptive transform, non-data-adaptive transform, block-matching and 3D/4D filtering

(BM3D and BM4D) filters29,30,31. Transform domain filtering methods optimize denoising by first transforming the noisy image into a different domain. This approach leverages specific

characteristics and noise properties of the transformed image for effective denoising. In the case of the BM4D filter, it performs nonlocal similarity characterizing on a set of consecutive

images by utilizing a technique called grouping and collaborative filtering. In the grouping stage, groups are formed as 3-D arrays of mutually similar blocks extracted from the set of

consecutive image frames. Several blocks from the same image may be included in a group, naturally taking advantage of the nonlocal similarity. Nonetheless, the majority of blocks that are

mutually related may often be identified along the temporal dimension. Then collaborative filtering generates unique estimates for each group by compressing the transform domain of the

individual group. When the prevalence of comparable groups next to one another and the high local correlation of the image data are confirmed, each individual group shows correlation in

measurements across all dimensions. Applying a decorrelating transformation to the grouped data will result in a sparse representation of the true signal. In contrast to BM3D filtering,

which can introduce artifacts and show limited effectiveness in denoising specific image regions, BM4D groups spatiotemporal volumes based on their similarities. In BM4D, the groups are 4D

stacks of 3D volumes, and collaborative filtering is performed using a separable 4D spatiotemporal transform. Due to the extreme sparsity of the 4D group spectrum, the noise reduction

achieved in BM4D is more successful compared to BM3D. This makes BM4D particularly effective in reducing noise in regions where visual attention is mainly focused. This paper introduces a

novel image-denoising method named BM4D, which utilizes block matching and four-dimensional filtering in the three-dimensional transform domain. The 3D transform offers superior mathematical

properties compared to commonly used wavelet or contourlet transforms, effectively capturing anisotropic image properties at various scales and directions. By extending BM3D into four 4D

spaces, the method significantly enhances edge and texture details in the images. We applied the 4D block matching filter to low-amplitude signal scans with low signal-to-noise ratio and

compared its performance with other denoising filters (Gaussian, median, and Wiener filters) using peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM)

evaluation. THEORY BM4D In the BM4D algorithm, noisy volumetric data is considered as observation z : X → ℝ of the form $$z(x) = y(x) + \eta (x),\quad x \in X$$ (1) Here, in this equation, y

is the original, unknown, and volumetric signal, x is a 3-D coordinate belonging to the signal domain \(X \subset {\mathbb{Z}}^{3},\) and \(\eta (\cdot ) \sim N(0, {\sigma }^{2})\) is

independent and identically distributed (i.i.d.) Gaussian noise with zero means and known standard deviation σ. BM4D works in two cascading stages, which are a hard-thresholding and a

Wiener-filtering stage. HARD-THRESHOLDING STAGE At the Hard-Thresholding Stage, the four-dimensional groups are created by stacking up noisy, three-dimensional cubes identical to

\({C}_{{x}_{R}}^{z}\) along a fourth additional dimension. Here, \({C}_{{x}_{R}}^{z}\) denotes a cube of \({L}^{3}\) where \(L \in {\mathbb{N}}\), extracted from noisy observation z at the

3D coordinate \({x}_{R} \in X\). More specifically, the photometric distance is used to calculate how similar two cubes are, which is defined by, $$d\left({C}_{{x}_{i}}^{z}

,{C}_{{x}_{j}}^{z}\right)= \frac{{\parallel {C}_{{x}_{i}}^{z} - {C}_{{x}_{j}}^{z}\parallel }_{2}^{2}}{{L}^{3}}$$ (2) where \({|| \cdot ||}_{2}^{2}\) denotes the sum of squared differences

between corresponding intensities of the two input cubes, and the denominator \({L}^{3}\) serves as a normalization factor. No prefiltering is performed before cube matching, so the

similarity of noise observations can be directly tested. In the grouping step, cubes similar to each other are extracted from z and combined to form a group for each cube

\({C}_{{x}_{R}}^{z}\). If the distance between two cubes was not larger than the predefined threshold \({\tau }_{match}^{ht}\), the two cubes are considered to be similar. Similarly, to

\({C}_{xR}^{z}\), we here firstly define a set that contains the indexes for the cubes as follows, $${S}_{{x}_{R}}^{z}=\left\{ {x}_{i} \in X : d\left({C}_{{x}_{R}}^{z} , {C}_{{x}_{i}}^{z}

\right)\le {\tau }_{match}^{ht}\right\}$$ (3) Then, a four-dimensional group is built by the above formula (being \({\coprod }\) the disjoint union operation): $${G}_{{S}_{{x}_{R}}^{z}}^{z}=

{\coprod }_{{x}_{i}\in {S}_{{x}_{R}}^{z} }{C}_{{x}_{i}}^{z}$$ (4) where the reference cube (represented by R) matches a set of similar cubes located in the 3D data. Particularly, the

coordinates \({x}_{R}\) and \({x}_{i}\) correspond to the tail and head of the arrow connecting the cubes in formula (4), respectively. In the collaborative filtering step, a joint

four-dimensional transformation \({T}_{4D}^{ht}\) was applied to each dimension of Eq. (5), respectively. Then, by a hard threshold operator \({\gamma }^{ht}\) with the threshold \(\sigma

{\lambda }_{4D}\), the obtained four-dimensional group spectrum is $${\gamma }^{ht} {( T}_{4D}^{ht} {(G}_{{S}_{{x}_{R}}^{z}}^{z}))$$ (5) Note that since the distance from any cube to itself

is always 0, according to the definition of formula (4), each formula (5) must contain at least its reference cube. Representing the filter group, it is transformed into the following form:

$${( T}_{4D}^{ht-1}({\gamma }^{ht} {( T}_{4D}^{ht} {(G}_{{S}_{{x}_{R}}^{z}}^{z})))= {\widehat{G}}_{{S}_{{x}_{R}}^{z}}^{y}= {\coprod }_{{x}_{i}\in {S}_{{x}_{R}}^{z}

}{\widehat{C}}_{{x}_{i}}^{y}$$ (6) For each unknown volume data y, the estimated \({\widehat{C}}_{{x}_{i}}^{y}\) of the original \({C}_{{x}_{i}}^{y}\) was extracted separately. Formula (6)

was an overcomplete representation of the denoising data because cubes in different groups, as well as cubes within the same group, are likely to overlap; thus, within the overlapping

regions, different cubes provide multiple, and in general different, estimates for the same voxel. In the aggregation step, such redundancy is exploited through an adaptive convex

combination to produce the basic volumetric estimate $${\widehat{y}}^{ht} = {\sum }_{{x}_{R\in X}} \frac{({\sum }_{{x}_{i\in {S}_{{x}_{R}}^{z}}} {\omega }_{xR}^{ht}

{\widehat{C}}_{{x}_{i}}^{y})}{({\sum }_{{x}_{i\in {S}_{{x}_{R}}^{z}}} {\omega }_{xR}^{ht} {\chi }_{{x}_{i}})}$$ (7) where \({\omega }_{xR}^{ht}\) are group-dependent weights, \({\chi

}_{{x}_{i}} : X \to \{0, 1\}\) is the characteristic (indicator) function of the domain of \({\widehat{C}}_{{x}_{i}}^{y}\) (i.e., \({\chi }_{{x}_{i}}\) = 1 over the coordinates of the voxels

of \({\widehat{C}}_{{x}_{i}}^{y}\) and \({\chi }_{{x}_{i}}\) = 0 elsewhere), and every \({\widehat{C}}_{{x}_{i}}^{y}\) is assumed to be zero-padded outside its domain. Note that, whereas in

BM3D, a 2-D Kaiser window of the same size as the blocks is used to alleviate blocking artefacts in the aggregated estimate, in the proposed BM4D, we do not perform such windowing because

of the small size of the cubes. The weights in Eq. (7) are defined as $${\omega }_{xR}^{ht}= \frac{1}{{{\sigma }^{2}N}_{{x}_{R}}^{ht}}$$ (8) where σ is the standard deviation of the noise in

z and \({N}_{{x}_{R}}^{ht}\) denotes the number of non-zero coefficients in Eq. (5). Since the DC (discrete cosine) coefficient is always retained after thresholding, i.e.,

\({N}_{{x}_{R}}^{ht}\) ≥ 1, the denominator of Eq. (8) is never zero. The number \({N}_{{x}_{R}}^{ht}\) has a double interpretation: on one hand, it measures the sparsity of the thresholded

spectrum (Eq. 5), and on the other, it approximates the total residual noise variance of the group estimate (Eq. 6). As a result, groups with higher correlation levels are rewarded with

bigger weights, whilst groups with higher residual noise levels are penalized with smaller weights. WIENER-FILTERING STAGE Following the preceding step, the BM4D algorithm employs Wiener

filtering, which is a well-established and widely used adaptive filter in signal processing32,33,34,35. The Wiener filter is known for its simplicity, stability, and speed, and has been

demonstrated to be an optimal filter in various signal-processing applications. Specifically, in BM4D, the Wiener filter is utilized to remove noise from each 3D block of wavelet

coefficients, allowing the algorithm to estimate the original, clean signal from the noisy input. $${P}_{wiener} = {\mu }_{m} +\frac{max\left(0, {\sigma }_{m}^{2} - {v}^{2} \right)

}{max\left(\sigma {m}^{2}, {v}^{2}\right)}\left({P}_{raw} - {\mu }_{m}\right)$$ (9) where \({P}_{raw}\) represents the raw data in the detector domain. Denoting \({\mu }_{m}\) and \({\sigma

}_{m}^{2}\) as local mean and local variance of \({P}_{raw}\) respectively, \({v}^{2}\) as the mean of local variance \({\sigma }_{m}^{2}\). \({P}_{wiener}\) is the denoising result after

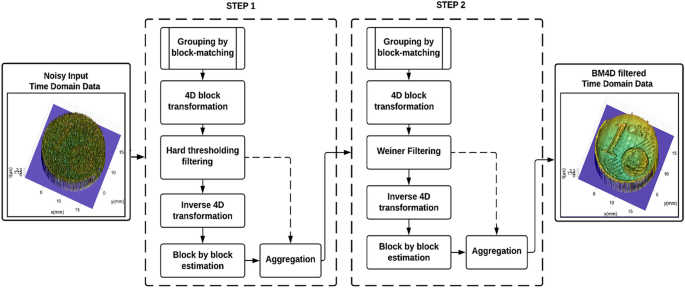
wiener filtering. Following the above steps, the BM4D filtering process is performed on noisy 3D domain data, and the final result is obtained after the Wiener filtering stage. FLOWCHART OF

THE ALGORITHM In this paper, the BM4D algorithm is used to denoise the acquired images through the experimental setup of SAM technique. The applied algorithm is further divided into two

steps. In the first step, the noisy 3D domain data is first grouped by block matching algorithm and step 1 filtered output is obtained by hard threshold filtering followed by estimation and

aggregation. After that, in the 2nd step, we applied the wiener filtering on the output of step 1. The final denoised output image is then collected at the end of step 2 after aggregating

the filtered blocks in the 4D domain. A flowchart of the working process of the applied BM4D algorithm is shown in Fig. 1. EXPERIMENTAL SETUP Figure 2 shows a labelled image of SAM, which is

used to acquire images of the sample. SAM uses reflection and transmission modes to create images that reveal different features of the sample. An image (Fig. 2) of SAM has been annotated

and is used for image acquisition. Further details regarding the working principles of these modes can be found elsewhere. In this article, we have focused on using the reflection mode to

scan the samples36. A concave spherical sapphire lens rod is frequently used to focus acoustic energy through a coupling medium (in this case, water), and ultrasonic signals are generated

from a signal generator and sent to the sample. After the waves bounce back the signals from the sample, they are detected and converted into a digital signal, which is called an A-scan or

amplitude scan. To create a C-scan image of the sample, this procedure is performed at different locations in the XY plane. Another way to visualize a C-scan is as the combination of A-scans

in two dimensions. A LabView program controlled a custom-built SAM, as depicted in Fig. 2, which incorporated a Standa high-precision scanning stage (8MTF-200-Motorized XY Microscope Stage)

for data collected during the experiment. In a previous study by the same group, a comparable experimental arrangement was used to account for inclined samples37. The acoustic imaging

capabilities were enabled using National Instruments' PXIe FPGA modules and FlexRIO hardware, which were housed in a PXIe chassis (PXIe-1082) containing an arbitrary waveform generator

(AT-1212). The transducer was excited using Mexican hat signals and boosted using an RF amplifier (AMP018032-T) to amplify the ultrasonic signals. The acoustical reflections produced by the

sample surface were amplified using a custom-designed amplifier, and then, they were further amplified with a custom-designed pre-amplifier and digitized using a 12-bit high-speed (1.6 GS/s)

digitizer (NI-5772). For ground truth, a 50 MHz focused transducer produced by Olympus was utilized, which had a 6.35 mm aperture and a 12 mm focal length. For this paper, a series of

experimental tests were conducted using a custom desised SAM in conjunction with a scanning stage. This stage was utilized to create a custom-designed ultrasonic scanning platform that could

be controlled using LabVIEW software, as described in detail in reference38. To implement the ultrasonic functionality of the microscope, we. During the experiments, the microscope was

focused on a point that was approximately in the middle of the sample. To minimize scanning time and turbulence caused by quick transducer motions, a serpentine mode was employed for stage

scanning. The entire experimental setup is illustrated in Fig. 2. In the beginning on the experiment a ground truth or reference scan was performed with 0.65 Vpp ( maximum 1 Vpp) from the

signal generator. Later on, 2 other experiments were performed with 0.24 and 0.25 Vpp, respectively. These 2 exepriments were considered as nosiy scanned data. ANALYSIS OF THE OUTPUT FROM

SAM For this experiment, a standard Euro 1-cent coin was scanned as a reference sample at various amplitudes. The scans obtained from the experiment under general conditions contain noises

which are introduced due to several reasons like environmental parameters, instrument and measurement error and other reasons. Later we tried to remove noises from these scans using the

proposed algorithm. The ground truth or almost noise-free scan is also obtained from the experiment where all the reading and scan parameters are taken in almost ideal conditions to reduce

noise parameters. Figure 3 shows the ground truth or the reference image which is finally used to compare with the results obtained via various denoising filters. QUALITATIVE ANALYSIS OF

DENOISED IMAGES In this paper, we explored different denoising filters to enhance the accuracy and obtain noise-free results for the time domain signals. Among the filters tested were the

Gaussian filter, median filter, Wiener filter, and 4D block matching (BM4D) filter. Notably, the BM4D filter demonstrated promising outcomes, prompting us to further improve the approach by

applying the 3D block matching filter to the denoised signal. To evaluate the filters' effectiveness in handling low-amplitude data, we used two sets of data with amplitudes of 0.24Vpp

and 0.25Vpp, respectively. Through thorough analysis and comparison, we determined that the BM4D filter, along with the supplementary 3D block matching filter, provided the most favorable

denoising results, making it an excellent choice for enhancing the quality of low-amplitude data in our study. In Fig. 4, we have presented the results of applying several denoising filters

to low-amplitude signal data with an amplitude of 0.24Vpp, in order to assess their effectiveness in improving the quality of the output. Specifically, we have included an amplitude image

and the corresponding line profile at the Y = 201 (shown by the yellow line) of the corresponding images, for each of the following denoising filters: (a) the original noisy data, (b) the

amplitude image after applying a Gaussian filter to the time domain signals of the noisy data, (c) the amplitude image after applying a median filter to the time domain signals of the noisy

data, (d) the amplitude image after applying a Wiener filter to the time domain signals of the noisy data, and (e) the amplitude image after applying a 4D block matching filter to the time

domain signals of the noisy data. Figure 4 provides clear evidence that the BM4D filter outperforms other filters in denoising the original noisy image. The image quality significantly

improves with the BM4D filter, surpassing the results obtained by other filters. The line profile analysis further confirms that the BM4D filter effectively reduces total noise in the image.

Moreover, the BM4D filter manages to retain the image structure while effectively removing most of the noise, demonstrating its superior denoising capabilities. This makes the BM4D filter a

preferred choice for achieving high-quality denoising results in our study. In Fig. 5, we have provided an assessment of the effectiveness of 4D and 3D block-matching filters in improving

the quality of the output obtained from processing low-amplitude signal data with an amplitude of 0.24Vpp. Specifically, the figure includes (a) the original noisy data, (b) the amplitude

image after applying a 4D block-matching (BM4D) filter to the time domain signals of the noisy data, and (c) the amplitude image after applying a 3D block-matching (BM3D) filter to the image

obtained from filtering the 4D block matching filtered data. Additionally, the corresponding line profile at the Y = 201 (shown by the yellow line) of the images is included in the figure.

After assessing the images in Fig. 5 qualitatively, we can observe that the BM4D filter does remove the noises from the original image effectively. But applying the BM3D filter on the

denoise image acquired from the BM4D algorithm substantially reduces the noises while also retaining image structure and overall quality. This assessment can also be verified from the line

profile which gives us a general idea of the overall performance of the combined BM4D and BM3D filter. Similarly in Fig. 6, we have presented the results of applying several denoising

filters to low amplitude signal data with an amplitude of 0.25Vpp, in order to assess their effectiveness in improving the quality of the output. Specifically, we have included an amplitude

image and the corresponding line profile at the Y = 201 (shown by the yellow line) of the corresponding images, for each of the following denoising filters: (a) the original noisy data, (b)

the amplitude image after applying a Gaussian filter to the time domain signals of the noisy data, (c) the amplitude image after applying a median filter to the time domain signals of the

noisy data, (d) the amplitude image after applying a Wiener filter to the time domain signals of the noisy data, and (e) the amplitude image after applying a 4D block matching filter to the

time domain signals of the noisy data. Furthermore, Fig. 7f–j includes the corresponding line profiles at Y = 201, indicated by the yellow line, for the images. In Fig. 7, we have provided

an assessment of the effectiveness of 4D and 3D block-matching filters in improving the quality of the output obtained from processing low amplitude signal data with an amplitude of 0.25Vpp.

Specifically, the figure includes (a) the original noisy data, (b) the amplitude image after applying a 3D block-matching filter to the time domain signals of the noisy data, (c) the

amplitude image is obtained by applying a 4D block-matching filter to the time domain signals of the noisy data, and (d) the amplitude image after applying a 3D block-matching filter to the

image obtained from filtering the 4D block matching filtered data. Additionally, the corresponding line profiles at the Y = 201 (shown by the yellow line) of the images are included in the

Fig. 7e–h. The denoising results clearly demonstrate that the BM4D filter is highly effective in reducing noise and enhancing the quality of low-amplitude signal data with an amplitude of

0.25Vpp. Compared to other conventional filters like Gaussian, median, and Wiener filters, the BM4D filter shows the best performance in terms of noise reduction and preserving image

structures. Moreover, the combination of BM4D and BM3D filters yields even better results, further enhancing the clarity of the denoised output. The line profiles of each denoised image also

verify the superiority of the BM4D filter in reducing noise. The proposed denoising algorithm consistently outperforms other conventional filters, resulting in the most accurate and

noise-free images. Figures 8 and 9 display the final denoised output of the BM4D filter, presenting denoised amplitude and time domain signal plots for both 0.24 Vpp and 0.25 Vpp low

amplitude signals. These figures reinforce the effectiveness and robustness of the proposed denoising algorithm in handling low-amplitude data and improving the overall image quality.

QUANTITATIVE ANALYSIS OF DENOISED IMAGES During the evaluation of the filtered output, we encountered an issue where the noisy data and the ground truth data had slight translation and

rotation deviations. This misalignment affected the accuracy of peak-signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM) evaluations, making it challenging to obtain

reliable results. To overcome this challenge, we utilized an image registration technique implemented through MATLAB. This technique allowed us to align the noisy data with the ground truth

data accurately, correcting for any translation and rotation deviations. As a result, we obtained more precise measurements of PSNR and SSIM, providing a more reliable assessment of the

denoising performance achieved by the various filters. With the corrected evaluations, we were able to confirm that the BM4D filter yielded the best denoising results, significantly reducing

noise while preserving the image's structural details. The line profile analysis further supported the effectiveness of the BM4D filter in reducing total noise in the image. Overall,

the application of the image registration technique provided a more comprehensive and accurate evaluation of the denoising algorithms' performance. Determining the similarity between

the ground truth (reference image) and filtered images is an essential component for calculating the peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM)39. A SAM

image with appropriate amplitude is chosen as the reference image, while a low amplitude SAM image is used as the sensed image. Once these images have been registered, they are compared

based on their content. After processing the low-amplitude data using various denoising filters, it was necessary to evaluate the quality of the output obtained. In this regard, two commonly

used measures, namely peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM), were employed to quantitatively assess the performance of the denoising filters. The

PSNR is a commonly used metric to evaluate the quality of a denoised signal by computing the ratio of the peak signal power to the mean squared error (MSE) between the original and the

denoised signal. Higher PSNR values indicate better performance of the denoising filter in preserving the signal quality. Similarly, the SSIM measures the structural similarity between the

original and the denoised signal by comparing their luminance, contrast, and structural information. SSIM values range from 0 to 1, where a value of 1 indicates a perfect match between the

original and denoised signals. The resulting PSNR and SSIM values obtained from the denoised signals of low amplitude data (0.24Vpp and 0.25Vpp) were tabulated in Tables 1 and 2 to

facilitate a direct comparison of the performance of each denoising filter. This evaluation process ensures the effectiveness of the proposed method for improving the quality of noisy

signals. The quantitative analysis based on the PSNR and SSIM values shows that the combined BM4D and BM3D filter shows the best result which has the highest PSNR and SSIM values followed by

the BM4D filter (Tables 1 and 2). Other applied conventional filter has lower performance compared to the proposed algorithm. We conducted a comprehensive analysis on the images, varying

the amplitude (0.24 V and 0.25 V) of the input signal. This approach was adopted to showcase the robustness and effectiveness of the proposed denoising method. The results of this analysis

are clearly presented in the tables (Tables 1 and 2), providing valuable insights into the performance of our method under different signal amplitudes. This in-depth analysis proves that our

proposed algorithm is best suited to denoise the noisy data acquired from the SAM technique. CONCLUSION In this paper, we have demonstrated a 4D block-matching filter can be used to denoise

the scanning acoustic microscopic volumetric signals. Here we demonestrated restoring the noisy data obtained at the low-amplitude signal scans or noisy images with a low signal-to-noise

ratio. The low amplitude signal data scanned are 0.25Vpp and 0.24Vpp. We have compared it with various conventional denoising filters such as the Gaussian filter, Median filter and Wiener

filter and compared the image with our proposed 4D & 3D block matching filter. From the visual inspection of the image and pondering over the peak signal-to-noise ratio (PSNR) and

structural similarity index measure (SSIM) values obtained, it is evident that the proposed block match filter performed better than the compared conventional denoising filters when applied

over time domain signals. The proposed block matching filter would be a good option in image denoising where the signal-to-noise ratio is poor, like in photoacoustic imaging (Supplementary

Information). DATA AVAILABILITY The authors declare the availability of the data and codes used in the research to obtain the results reported in the manuscript upon reasonable request from

the corresponding author. REFERENCES * Briggs, A. & Kolosov, O. _Acoustic Microscopy_ (Oxford University Press, 2010). Google Scholar  * Hofmann, M. _et al._ Scanning acoustic

microscopy—A novel noninvasive method to determine tumor interstitial fluid pressure in a xenograft tumor model. _Transl. Oncol._ 9(3), 179–183 (2016). Article  PubMed  PubMed Central 

Google Scholar  * Habib, A. _et al._ Mechanical characterization of sintered piezo-electric ceramic material using scanning acoustic microscope. _Ultrasonics_ 52(8), 989–995 (2012). Article

  CAS  PubMed  Google Scholar  * Bauermann, L. P. _et al._ Scanning acoustic microscopy as a non-destructive imaging tool to localize defects inside battery cells. _J. Power Sources Adv._ 6,

100035 (2020). Article  Google Scholar  * Wagle, S., Habib, A. & Melandsø, F. Ultrasonic measurements of surface defects on flexible circuits using high-frequency focused polymer

transducers. _Jpn. J. Appl. Phys._ 56(7S1), 07JC05 (2017). Article  Google Scholar  * Karbhari, V. M. _Non-Destructive Evaluation (NDE) of Polymer Matrix Composites_ (Elsevier, 2013). Book 

Google Scholar  * Habib, A. _et al._ Quantitative ultrasonic characterization of c-axis oriented polycrystalline AlN thin film for smart device application. _Acta Acust. Acust._ 101(4),

675–683 (2015). Article  Google Scholar  * Wolf, M., Nair, A. S., Hoffrogge, P., Kühnicke, E. & Czurratis, P. Improved failure analysis in scanning acoustic microscopy via advanced

signal processing techniques. _Microelectron. Reliab._ 138, 114618 (2022). Article  Google Scholar  * Brand, S., Czurratis, P., Hoffrogge, P. & Petzold, M. Automated inspection and

classification of flip-chip-contacts using scanning acoustic microscopy. _Microelectron. Reliab._ 50(9–11), 1469–1473 (2010). Article  CAS  Google Scholar  * Fan, L., Zhang, F., Fan, H.

& Zhang, C. Brief review of image denoising techniques. _Vis. Comput. Indus. Biomed. Art_ 2(1), 1–12 (2019). CAS  Google Scholar  * Liu, D. & Chen, X. Image denoising based on

improved bidimensional empirical mode decomposition thresholding technology. _Multimed. Tools Appl._ 78, 7381–7417 (2019). Article  Google Scholar  * Malladi, S. R. S., Ram, S. &

Rodríguez, J. J. Image denoising using superpixel-based PCA. _IEEE Trans. Multimed._ 23, 2297–2309 (2020). Article  Google Scholar  * Li, P., Wang, H., Li, X. & Zhang, C. An image

denoising algorithm based on adaptive clustering and singular value decomposition. _IET Image Proc._ 15(3), 598–614 (2021). Article  Google Scholar  * Wang, Y., Ma, Q., Zhu, Q., Liu, X.

& Zhao, L. An intelligent approach for engine fault diagnosis based on Hilbert–Huang transform and support vector machine. _Appl. Acoust._ 75, 1–9 (2014). Article  CAS  Google Scholar  *

Fan, S., Han, W., Gao, Z., Yin, R. & Zheng, Y. Denoising algorithm for the FY-4A GIIRS based on principal component analysis. _Remote Sens._ 11(22), 2710 (2019). Article  ADS  Google

Scholar  * Liu, H. _et al._ High-precision sensor tuning of proton precession magnetometer by combining principal component analysis and singular value decomposition. _IEEE Sens. J._ 19(21),

9688–9696 (2019). Article  ADS  Google Scholar  * Tian, C. _et al._ Deep learning on image denoising: An overview. _Neural Netw._ 131, 251–275 (2020). Article  PubMed  MATH  Google Scholar

  * Ghose, S., Singh, N. & Singh, P. Image denoising using deep learning: Convolutional neural network. in _2020 10th International Conference on Cloud Computing, Data Science &

Engineering (Confluence)_. 511–517 (IEEE, 2020). * Gu, S. & Timofte, R. A brief review of image denoising algorithms and beyond. in _Inpainting and Denoising Challenges_. 1–21 (2019). *

Jadhav, S., Kuchibhotla, R., Agarwal, K., Habib, A. & Prasad, D. K. Deep learning-based denoising of acoustic images generated with point contact method. _J. Nondestruct. Evaluat. Diagn.

Prognost. Eng. Syst._ 6(3), 1–18 (2023). Google Scholar  * Singh, H., Ahmed, A. S., Melandsø, F. & Habib, A. Ultrasonic image denoising using machine learning in point contact

excitation and detection method. _Ultrasonics_ 127, 106834 (2023). Article  PubMed  Google Scholar  * Zhang, K., Zuo, W., Chen, Y., Meng, D. & Zhang, L. Beyond a gaussian denoiser:

Residual learning of deep cnn for image denoising. _IEEE Trans. Image Process._ 26(7), 3142–3155 (2017). Article  ADS  MathSciNet  PubMed  MATH  Google Scholar  * Hinton, G. E. Deep belief

networks. _Scholarpedia_ 4(5), 5947 (2009). Article  ADS  Google Scholar  * Vincent, P. _et al._ Stacked denoising autoencoders: Learning useful representations in a deep network with a

local denoising criterion. _J. Mach. Learn. Res._ 11(12), 3371 (2010). MathSciNet  MATH  Google Scholar  * Forsyth, D. A. _et al._ Object recognition with gradient-based learning. _Shape

Contour Group. Comput. Vis._ 332, 319–345 (1999). Google Scholar  * Wang, X., Girshick, R., Gupta, A. & He, K. Non-local neural networks. in _Proceedings of the IEEE Conference on

Computer Vision and Pattern Recognition_. 7794–7803 (2018). * Chan, T.-H. _et al._ PCANet: A simple deep learning baseline for image classification?. _IEEE Trans. Image Process._ 24(12),

5017–5032 (2015). Article  ADS  MathSciNet  PubMed  MATH  Google Scholar  * Yu, H., Ding, M., Zhang, X. & Wu, J. PCANet based nonlocal means method for speckle noise removal in

ultrasound images. _PLoS ONE_ 13(10), e0205390 (2018). Article  PubMed  PubMed Central  Google Scholar  * Yue, Z., Yong, H., Zhao, Q., Meng, D. & Zhang, L. Variational denoising network:

Toward blind noise modeling and removal. _Adv. Neural Inf. Process. Syst._ 32, 113 (2019). Google Scholar  * Hasan, M. & El-Sakka, M. R. Improved BM3D image denoising using

SSIM-optimized Wiener filter. _EURASIP J. Image Video Process._ 2018, 1–12 (2018). Article  Google Scholar  * Danielyan, A., Katkovnik, V. & Egiazarian, K. BM3D frames and variational

image deblurring. _IEEE Trans. Image Process._ 21(4), 1715–1728 (2011). Article  ADS  MathSciNet  PubMed  MATH  Google Scholar  * Danielyan, A., Foi, A., Katkovnik, V. & Egiazarian, K.

Spatially adaptive filtering as regularization in inverse imaging: Compressive sensing, super-resolution, and upsampling. in _Super-Resolution Imaging_. 123–154 (CRC Press, 2017). *

Maggioni, M., Katkovnik, V., Egiazarian, K. & Foi, A. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. _IEEE Trans. Image Process._ 22(1), 119–133

(2012). Article  ADS  MathSciNet  PubMed  MATH  Google Scholar  * Harold, J., Kushner, G. & Yin, G. Stochastic approximation and recursive algorithm and applications. _Appl. Math._ 35,

316 (1997). Google Scholar  * Egiazarian, K., Foi, A. & Katkovnik, V. Compressed sensing image reconstruction via recursive spatially adaptive filtering. in _2007 IEEE International

Conference on Image Processing. _Vol. 1. I-549–I-552 (IEEE, 2007). * Somani, A., Banerjee, P., Rastogi, M., Agarwal, K., Prasad, D.K. & Habib, A. Image inpainting with hypergraphs for

resolution improvement in scanning acoustic microscopy. in _Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition_. 3112–3121 (2023). * Kumar, P. _et al._

Numerical method for tilt compensation in scanning acoustic microscopy. _Measurement_ 187, 110306 (2022). Article  Google Scholar  * Banerjee, P. _et al._ Image inpainting in acoustic

microscopy. _AIP Adv._ 13(4), 4 (2023). Article  Google Scholar  * Hore, A. & Ziou, D. Image quality metrics: PSNR vs. SSIM. in _2010 20th International Conference on Pattern

Recognition_. 2366–2369 (IEEE, 2010). Download references ACKNOWLEDGEMENTS The following funding is acknowledged: Cristin Project, Norway, ID: 2061348 (Habib). The publication charges for

this article have been funded by a grant from the publication fund of the UiT The Arctic University of Norway. FUNDING Open access funding provided by UiT The Arctic University of Norway

(incl University Hospital of North Norway). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Chemical Engineering, Indian Institute of Technology, Guwahati, India Shubham Kumar

Gupta * Department of Electronics and Electrical Engineering, Indian Institute of Technology, Guwahati, India Rishant Pal * Department of Physics and Technology, UiT The Arctic University of

Norway, Tromsø, Norway Azeem Ahmad, Frank Melandsø & Anowarul Habib Authors * Shubham Kumar Gupta View author publications You can also search for this author inPubMed Google Scholar *

Rishant Pal View author publications You can also search for this author inPubMed Google Scholar * Azeem Ahmad View author publications You can also search for this author inPubMed Google

Scholar * Frank Melandsø View author publications You can also search for this author inPubMed Google Scholar * Anowarul Habib View author publications You can also search for this author

inPubMed Google Scholar CONTRIBUTIONS A.H. conceptualized, designed, and developed the scanning acoustic microscope. A.A. and A.H. performed the experiments and conceptualized the idea.

S.K.G. and R.P. analyze the data, developed the algorithm, wrote the original draft, reviewing, and editing the manuscript with support from all co-authors. Funding was secured by F.M. and

A.H. CORRESPONDING AUTHOR Correspondence to Anowarul Habib. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION. RIGHTS AND

PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any

medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The

images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is

not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission

directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Gupta,

S.K., Pal, R., Ahmad, A. _et al._ Image denoising in acoustic microscopy using block-matching and 4D filter. _Sci Rep_ 13, 13212 (2023). https://doi.org/10.1038/s41598-023-40301-7 Download

citation * Received: 17 April 2023 * Accepted: 08 August 2023 * Published: 14 August 2023 * DOI: https://doi.org/10.1038/s41598-023-40301-7 SHARE THIS ARTICLE Anyone you share the following

link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature

SharedIt content-sharing initiative