Canonical hamiltonian ensemble representation of dephasing dynamics and the impact of thermal fluctuations on quantum-to-classical transition

ABSTRACT An important mathematical tool for studying open quantum system theory, which studies the dynamics of a reduced system, is the completely positive and trace-preserving dynamical

linear map parameterized by a special parameter-time. Counter-intuitively, akin to the Fourier transform of a signal in time-sequence to its frequency distribution, the time evolution of a

reduced system can also be studied in the frequency domain. A recent proposed idea which studies the representation of dynamical processes in the frequency domain, referred to as canonical

Hamiltonian ensemble representation (CHER), proved its capability of characterizing the noncalssical traits of the dynamics. Here we elaborate in detail the theoretical foundation within a

unified framework and demonstrate several examples for further studies of its properties. In particular, we find that the thermal fluctuations are clearly manifested in the manner of

broadening CHER, and consequently rendering the CHER less nonclassical. We also point out the discrepancy between the notions of nonclassicality and non-Markovianity, show multiple CHERs

beyond pure dephasing, and, finally, to support the practical viability, propose an experimental realization based upon the free induction decay measurement of nitrogen-vacancy center in

diamond. SIMILAR CONTENT BEING VIEWED BY OTHERS EFFECTS OF SYMMETRY BREAKING OF THE STRUCTURALLY-DISORDERED HAMILTONIAN ENSEMBLES ON THE ANISOTROPIC DECOHERENCE OF QUBITS Article Open access

21 February 2022 STOCHASTIC SCHRÖDINGER EQUATION DERIVATION OF NON-MARKOVIAN TWO-TIME CORRELATION FUNCTIONS Article Open access 04 June 2021 QUANTUM MANY-BODY SCARS AND WEAK BREAKING OF

ERGODICITY Article 27 May 2021 INTRODUCTION The ubiquity of the open quantum theory has attracted many attentions among the quantum physics community, with applications ranging from physics,

chemistry, to biology1,2,3,4,5,6,7,8,9, note to mention its fundamental importance in the development of frontier technologies10,11,12. Irrespective of the unitary time evolution of the

total system–environment arrangement, the reduced system dynamics typically exhibits an incoherent behaviour after dropping the inaccessible ambient environment. One of the main causes of

such incoherent behaviour stems from the loss of information on the system–environment correlations, which comes from the interactions between the system and its ambient environment, and

significantly modulate the properties of the reduced system dynamics, e.g., from Markovianity to non-Markovianity13,14,15,16,17,18. Generically, such incoherent dynamics are described in

terms of a family of _time_-parametrized completely positive and trace-preserving (CPTP) maps acting on the system density matrices19,20,21,22. However, since the set of CPTP maps does not

form a well-characterized algebraic structure, its mathematical characterization is nontrivial; consequently, it stimulates the development of several different, but intimately related,

techniques for characterizing CPTP maps, including operator-sum representation, Kraus operators23, process matrices24, and Choi–Jamiołkowski isomorphism25,26. In addition, to derive

appropriate equations of motion governing the open system dynamics, one typically adopts an assumption of Born–Markov approximation, which leads to the master equation in the standard

Lindblad form27,28. However, practical problems, e.g., with strong system–environment interactions and/or when long-lived environmental correlations play significant roles, usually do not

meet this assumption. To go beyond the Born–Markov regime while taking the memory effects into account, many efforts have been devoted to the construction of improved techniques, such as

path-integral formalisms29,30,31, hierarchy equations of motion (HEOM)32,33,34, the reaction-coordinate method35,36, and non-Markovian quantum master equations37,38,39. In the aforementioned

approaches, the dynamics of a reduced system has been studied along the time-axis; nevertheless, conventional time evolutions can be studied from a brand new viewpoint. Let us first recall

that Fourier transform, which transforms signals in time domain to a frequency domain, enables one to study and manipulate the characters of the signal in the frequency domain. Then, a

similar picture emerges where a bosonic field can be described with the Wigner function40 or the Glauber–Sudarshan _P_ representations41,42. These are (quasi-)distribution functions over

certain corresponding phase spaces, rather than real spaces, and are capable of characterizing the nonclassical features of the boson field. On the other hand, even a century after the birth

of quantum theory, the essential quantum nature and the question of distinguishing the genuine quantum traits from classical counterparts remain contentious and intriguing due to the

fundamental importance. In particular, the boundary between quantum and classical realm and how classical characters emerge from quantum essence have given rise to vast debates43,44,45,46.

Inspired by the above insights, we have proposed to describe a unital dynamics with a (quasi-)distribution function over frequency domain, referred to as the canonical Hamiltonian ensemble

representation (CHER)47,48. In order to acquire additional properties of the CHER, exploring its versatility in characterizing the nonclassicality of unital dynamics, and the impact of

thermal fluctuations, here we first elaborate in detail the theoretical foundation within a unified framework and recast it into Fourier transform formalism. We then demonstrate several

examples of qubit pure dephasing dynamics with or without revealing nonclassical traits. We conclude that, generically, increasing the environmental temperature broadens the CHERs and leads

to shallower negative wings, i.e., diminishment of nonclassical traits. This agrees with the usual intuition that thermal fluctuations are detrimental to the quantum nature and constitute

one of the primary origins of quantum-to-classical transitions. Furthermore, by varying the Ohmicity of the spectral density and the environmental temperature, we can observe a transition

between Markovianity and non-Markovianity as well as competition between non-Markovian memory effect and Markovian thermal fluctuations. These phenomena can be easily understood from the

deformation of the CHERs. Our results suggest that the notion of nonclassicality is different from the non-Markovianity. Further studies on distinguishing the two notions are highly desired.

We have also discussed the uniqueness of CHER for pure dephasing dynamics, which is underpinned by the abelian algebraic structure of the Hamiltonian ensemble (HE). Therefore, one can

expect the breakdown of uniqueness when going beyond pure dephasing. To explicitly show this breakdown of uniqueness, we consider an example of general qubit unital dynamics. Based on the

approach we have established, one has redundant freedom in constructing the CHER for unital dynamics. Upon arriving at a CHER for a unital dynamics, one can arbitrarily generate more CHERs

by adding high order spherical harmonics with \(l\ge 3\) to the known one. Notably, these CHERs lead to the same qubit unital dynamics. We therefore draw the conclusion that there are

multiple representations for unital dynamics. Finally, we have elucidated a promising experimental proposal based on the free induction decay measurement of the electron spin associated with

a diamond defect. Due to the three-order difference between spin qubit relaxation time \(T_1\) and dephasing time \(T_2^*\), the qubit dynamics can be well approximated by pure dephasing.

Therefore, the dynamical behaviour and the corresponding CHER can be determined experimentally by using a variant of Ramsey pulse sequence. This circumvents the burden of performing the

standard quantum process tomography experiment, meanwhile underpinning the practical viability and the compatibility of CHER theory with present-day techniques. RESULTS AVERAGED DYNAMICS

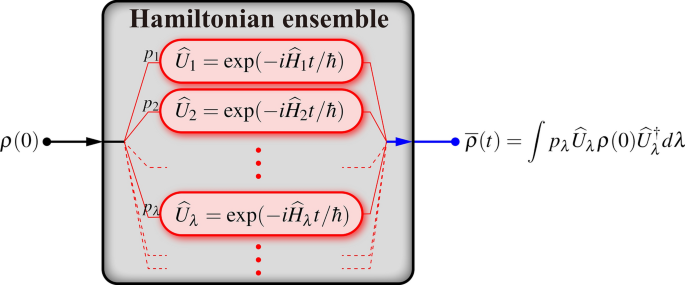
UNDER HE The mathematical tool of fundamental importance in this work is the Hamiltonian ensemble (HE). A HE \(\{(p_\lambda ,\widehat{H}_\lambda )\}_\lambda\) consists of a collection of

(time-independent) Hermitian operators \(\widehat{H}_\lambda\) of the same dimension, and a probability distribution \(p_\lambda\) of occurrence. The index \(\lambda\) is generic and may be

continuous and/or a multi-index. Each member Hamiltonian \(\widehat{H}_\lambda\) generates a unitary time-evolution operator \(\widehat{U}_\lambda =\exp (-i\widehat{H}_\lambda t/\hbar )\).

For each single run of an experiment, we input an initial state \(\rho (0)\) into the HE, which randomly assigns \(\rho (0)\) to a unitary channel \(\widehat{U}_\lambda\) according to the

probability distribution \(p_\lambda\) (Fig. 1). The ensemble-averaged dynamics after many runs is given by the unital map $$\begin{aligned} \overline{\rho }(t)=\mathcal {E}_t\{\rho

(0)\}=\int p_\lambda \widehat{U}_\lambda \rho (0)\widehat{U}_\lambda ^\dagger d\lambda . \end{aligned}$$ (1) Due to the averaging procedure over all unitary realizations, the time-evolved

state \(\overline{\rho }(t)\) undergoes a dephasing dynamics and behaves incoherently49,50,51,52. An instructive example50 is on a single qubit subject to spectral disorder with HE given by

\(\{(p(\omega ),\hbar \omega {\hat{\sigma }}_z/2)\}_\omega\); i.e., all the member Hamiltonian operators are proportional to \({\hat{\sigma }}_z\) with fluctuating energy level spacing

\(\hbar \omega\) and \(p(\omega )\) can be any probability distribution function. The resulting dynamics is pure dephasing $$\begin{aligned} \overline{\rho }(t)=\int _{-\infty }^\infty

p(\omega )e^{-i\omega {\hat{\sigma }}_zt/2}\rho _0e^{i\omega {\hat{\sigma }}_zt/2}d\omega =\left[ \begin{array}{cc} \rho _{\uparrow \uparrow } &{} \rho _{\uparrow \downarrow }\phi (t) \\

\rho _{\downarrow \uparrow }\phi ^*(t) &{} \rho _{\downarrow \downarrow } \end{array} \right] , \end{aligned}$$ (2) with the dephasing factor \(\phi (t)=\int p(\omega )e^{-i\omega

t}d\omega\) being the Fourier transform of \(p(\omega )\). Since each time-evolution operator \(\widehat{U}_\omega =\exp (-i\omega {\hat{\sigma }}_zt/2)\) has a geometric interpretation,

namely, an unitary rotation about the _z_-axis of the Bloch sphere at an angular velocity \(\omega\), the above HE, as well as the resulting pure dephasing dynamics (2), can be schematically

illustrated in terms of random phase (Fig. 2). The ensemble of red arrows in Fig. 2a denotes the random unitary rotations generated by the member Hamiltonian operators \(\hbar \omega

{\hat{\sigma }}_z/2\) weighted by the probability distribution \(p(\omega )\). The ensemble average results in the blue arrow, whose dynamical behaviour is pure dephasing due to the random

phase of the ensemble of red arrows. Consequently, such HE-description of pure dephasing agrees with the conventional interpretation of random phase and capable of providing further insights

into the algebraic structure behind the dephasing dynamics48. Additionally, whenever the probability distribution function \(p(\omega )\) is specified, the pure dephasing dynamics (2) is

fully determined. This implies that, as illustrated in Fig. 2b, one can use \(p(\omega )\) to characterize the qubit pure dephasing dynamics, and can be recovered by the Fourier transform in

Eq. (2). Particularly, as \(p(\omega )\) is distributee over the angular velocity \(\omega\) and is related to the pure dephasing via the Fourier transform, it becomes a representation of

qubit pure dephasing in the frequency domain. It is worth noting that the concept of HE is originally proposed to describe the influence of a disordered environment49,50; whereas the

experimental realizations of the controlled dephasing are achieved in a similar spirit of statistical mixture53,54,55, and the revival of quantum correlations in the absence of back-action

has also been studied in terms of similar ensemble description56,57. CANONICAL HAMILTONIAN-ENSEMBLE REPRESENTATION Exploration of the full power of the (quasi-)probability representation in

the frequency domain, referred to as CHER, and its ability to characterize the nonclassical nature of dephasing dynamics is undertaken here. In the case of _n_-dimension, both member

Hamiltonian operators \(\widehat{H}_\lambda\) and density matrices \(\rho\) are Hermitian and belong to the Lie algebra \(\mathfrak {u}(n)=\mathfrak {u}(1)\oplus \mathfrak {su}(n)\). Every

\(\widehat{H}_\lambda \in \mathfrak {u}(n)\) is a linear combination $$\begin{aligned} \widehat{H}_\lambda =\lambda _0\widehat{I}+\sum _{m=1}^{n^2-1} \lambda _m\widehat{L}_m=\lambda

_0\widehat{I}+\vec {\lambda }\cdot \widehat{\varvec{L}} \end{aligned}$$ (3) of identity operator \(\widehat{I}\) and \(n^2-1\) traceless Hermitian generators \(\widehat{L}_m\) of \(\mathfrak

{su}(n)\); and so does \(\rho\). Therefore, the index \(\lambda =\{\lambda _0,\vec {\lambda }\}\) parameterizing the HE consists of two components, \(\lambda _0\in \mathbb {R}\) and \(\vec

{\lambda }=\{\lambda _m\}_m\in \mathbb {R}^{n^2-1}\). In order to highlight the role of the representation of a time evolution in the frequency domain played by \(p_\lambda\) encapsulated

within the HE, we will recast Eq. (1) into a similar form to Fourier transform. This is achieved with the help of several Lie algebra techniques. To investigate further, we begin with

$$\begin{aligned} \exp \left( -i\widehat{H}_\lambda t\right) \rho \exp \left( i\widehat{H}_\lambda t\right) =\sum _{\mu =0}^\infty \frac{(-it)^\mu }{\mu !}\left[ \widehat{H}_\lambda ,\rho

\right] _{(\mu )}, \end{aligned}$$ (4) where we have set \(\hbar =1\) so that \(\lambda\) is in unit of angular frequency, and the multiple commutators are defined as

$$\begin{aligned}&\left[ \widehat{H}_\lambda ,\rho \right] _{(0)}=\rho , \end{aligned}$$ (5) $$\begin{aligned}&\left[ \widehat{H}_\lambda ,\rho \right] _{(1)}=\left[

\widehat{H}_\lambda ,\rho \right] , \end{aligned}$$ (6) and $$\begin{aligned} \left[ \widehat{H}_\lambda ,\rho \right] _{(\mu )}=\left[ \widehat{H}_\lambda ,\left[ \widehat{H}_\lambda ,\rho

\right] _{(\mu -1)}\right] . \end{aligned}$$ (7) Since every density matrix \(\rho =n^{-1}\widehat{I}+\vec {\rho }\cdot \widehat{\varvec{L}}\) enjoys the same linear combination as Eq. (3),

the commutator in Eq. (6) is determined by \(n^2-1\) components \([\widehat{H}_\lambda ,\widehat{L}_m]=\widehat{M}_{\lambda ,m}\in \mathfrak {su}(n)\) as $$\begin{aligned} \left[

\widehat{H}_\lambda ,\rho \right] =\sum _{m=1}^{n^2-1}\rho _m\widehat{M}_{\lambda ,m} =\vec {\rho }\cdot \widehat{\varvec{M}}_\lambda . \end{aligned}$$ (8) Note that \([\widehat{H}_\lambda

,\widehat{I}]=0\). Furthermore, as each \(\widehat{M}_{\lambda ,m}\) is also an element in \(\mathfrak {su}(n)\), it can be expanded as a linear combination as well: $$\begin{aligned}

\widehat{M}_{\lambda ,m}=\vec {h}_{\lambda ,m}\cdot \widehat{\varvec{L}}, \end{aligned}$$ (9) where each \(\vec {h}_{\lambda ,m}\) is an \((n^2-1)\)-dimensional real vector for \(m=1,\ldots

,n^2-1\). Accordingly, the action of the commutator \([\widehat{H}_\lambda ,\quad ]\) can be conceived as an endomorphism in the sense that it maps a generator \(\widehat{L}_m\in \mathfrak

{su}(n)\) to the other element \(\widehat{M}_{\lambda ,m}\in \mathfrak {su}(n)\) and \(\widehat{I}\) to 0; consequently, we can uniquely associate each member Hamiltonian

\(\widehat{H}_\lambda\) with a linear map \(\widetilde{H}_\lambda :\mathfrak {u}(n)\rightarrow \mathfrak {u}(n)\), referred to as the adjoint representation of \(\widehat{H}_\lambda\), whose

action can be expressed in terms of usual matrix multiplication: $$\begin{aligned} \left[ \widehat{H}_\lambda ,\rho \right] \Rightarrow \widetilde{H}_\lambda \{\rho \}= \left[

\begin{array}{c|ccc} 0 &{} 0 &{} \cdots &{} 0 \\ \hline 0 &{} &{} &{} \\ \vdots &{} \vec {h}_{\lambda ,1} &{} \cdots &{} \vec {h}_{\lambda ,n^2-1} \\ 0

&{} &{} &{} \end{array} \right] \cdot \left[ \begin{array}{c} n^{-1} \\ \hline \\ \vec {\rho } \\ \\ \end{array} \right] . \end{aligned}$$ (10) It is straightforward to see that

the multiple commutator in Eq. (7) can be expressed in terms of the adjoint representation \([\widehat{H}_\lambda ,\rho ]_{(\mu )}\Rightarrow \widetilde{H}_\lambda ^\mu \{\rho \}\), as well

as Eq. (4) in the adjoint representation $$\begin{aligned} \exp \left( -i\widehat{H}_\lambda t\right) \rho \exp \left( i\widehat{H}_\lambda t\right) \Rightarrow \sum _{\mu =0}^\infty

\frac{(-it)^\mu }{\mu !}\widetilde{H}_\lambda ^\mu \{\rho \}=\exp (-i\widetilde{H}_\lambda t)\{\rho \}. \end{aligned}$$ (11) Along with above equations, for a given time-independent HE

\(\{(\wp _\lambda ,\widehat{H}_\lambda )\}_\lambda\), we can recast the right hand side of Eq. (1) into a Fourier transform expression from a (quasi-)distribution \(\wp _\lambda\), on a

locally compact group \(\mathcal {G}\) parameterized by \(\lambda =\{\lambda _0,\vec {\lambda }\}\), to the dynamical linear map \(\mathcal {E}_t^{(\widehat{L})}\)48: $$\begin{aligned}

\mathcal {E}_t^{(\widetilde{L})}=\int _\mathcal {G}\wp _\lambda e^{-i\lambda \widetilde{L}t}d\lambda . \end{aligned}$$ (12) Then the action of \(\mathcal {E}_t\) on a density matrix \(\rho\)

can be expressed in terms of usual matrix multiplication $$\begin{aligned} \mathcal {E}_t\{\rho \}\Rightarrow \mathcal {E}_t^{(\widehat{L})}\cdot \rho . \end{aligned}$$ (13) Note that the

\(\rho\) on the left hand side of Eq. (13) is an \(n\times n\) density matrix, while the one on the right hand side is an \(n^2\)-dimensional real vector \(\rho =\{n^{-1},\vec {\rho }\}\).

The equation is valid in the sense of the linear combination \(\rho =n^{-1}\widehat{I}+\vec {\rho }\cdot \widehat{\varvec{L}}\). Equation (12) associates a (quasi-)distribution \(\wp

_\lambda\) with the dynamical process \(\mathcal {E}_t\), $$\begin{aligned} \wp _\lambda \mapsto \mathcal {E}_t^{(\widetilde{L})}, \end{aligned}$$ (14) via the Fourier transform on group

formalism. This manifests that the role of \(\wp _\lambda\) as a CHER for \(\mathcal {E}_t\). Moreover, in the above formalism, we have replaced \(p_\lambda\) with \(\wp _\lambda\) to

incorporate the possibility that \(\wp _\lambda\) may contain negative values. The underlying physical meaning is an indicator of the nonclassical nature in the dynamical process \(\mathcal

{E}_t\). This will be clarified in the following discussion. VIRTUAL CLASSICAL ENVIRONMENT Suppose that a system \(\rho\) undergoes an averaged dynamics governed by a HE \(\{(p_\lambda

,\widehat{H}_\lambda )\}_\lambda\) with \(p_\lambda\) being a legitimate probability distribution. Equation (1) has implicitly assumed that the system is isolated in the sense that, beside

the uncertainty described by \(p_\lambda\), there is no other redundant environmental degree of freedom. However, Eq. (1) results in an incoherent dynamical behaviour, which arises as a

consequence of the ensemble average. This is reminiscent of open quantum systems50, where the incoherent properties are caused by the interaction to the environment. Now we can further

strengthen this connection between a HE and an open system dynamics by fabricating a virtual environment for a HE encapsulating a legitimate probability distribution \(p_\lambda\). Let

\(\{|\lambda \rangle \}_\lambda\) be an orthonormal basis for the environmental Hilbert space and \(\rho _{\rm E}=\int p_\lambda |\lambda \rangle \langle \lambda |d\lambda\) be the virtual

environment, then the averaged dynamics in Eq. (1) coincides with the open system dynamics, \(\mathcal {E}_t\{\rho (0)\}={\rm Tr}_{\rm E}\rho _{\rm T}(t)\), reduced from the total system

$$\begin{aligned} \rho _{\rm T}(t)=\widehat{U}_{\rm T} \left[ \rho (0)\otimes \rho _{\rm E}\right] \widehat{U}^\dagger _{\rm T} \end{aligned}$$ (15) by tracing over the environmental Hilbert

space. The total unitary operator \(\widehat{U}_{\rm T}=\int \exp (-i\widehat{H}_\lambda t)\otimes |\lambda \rangle \langle \lambda |d\lambda\) is generated by the total Hamiltonian

\(\widehat{H}_{\rm T}=\int \widehat{H}_\lambda \otimes |\lambda \rangle \langle \lambda |d\lambda\) acting both on the system and the environmental Hilbert spaces. Additionally, it is

noteworthily that the system and the virtual environment in \(\rho _{\rm T}(t)\) are at most classically correlated during the evolution, without establishing quantum discord58,59.

Consequently, the effect of the uncertainty \(p_\lambda\) in the HE can be resembled by fabricating a virtual environment, which is classically correlated to the system during the evolution.

PROCESS NONCLASSICALITY On the other hand, for a genuine quantum system, the inevitable interaction with its environment and the resulting bipartite correlations established during their

evolution constitute the primary cause of the incoherent behaviour. As a result, one naive way to characterize the incoherent dynamical processes is based on the properties of the

system–environment correlations. Nevertheless, as the environment typically consists of a hug degrees of freedom and cannot be fully accessed in most practical situations, this prevents the

viability of this naive approach. Inspired by the analogy between HE and a classical environment and to circumvent the practical difficulties, we propose an alternative definition of process

(non)classicality according to the (im)possibility to simulate the open system with a legitimate HE47. The underlying idea of our definition is to deliberately ignore the inaccessible

actual environment and try to interpret its effects classically in terms of HE-simulation; meanwhile, the definition relies only on the properties of the system properties, irrespective of

the inaccessible environment. For a given dynamical process \(\mathcal {E}_t\), whenever one is able to simulate it with a legitimate HE, i.e., its CHER in Eq. (12) is a legitimate

probability distribution, \(\mathcal {E}_t\) admits a classical interpretation of mixture of random rotations, and we call such \(\mathcal {E}_t\) classical-like, irrespective of actual

system–environment correlations. On the other hand, if its CHER necessarily contains negative values, this witnesses the establishment of quantum correlations during the evolution, and the

dynamics is nonclassical. Further rigorous proof is shown in Ref. 47, relying on the technique of group theory. CHER OF QUBIT PURE DEPHASING REDUCED FROM SPIN-BOSON MODEL To explicitly

exemplify the concept of CHER and the impact of thermal fluctuations, we consider the spin-boson model with total Hamiltonian $$\begin{aligned} \widehat{H}_{\rm T}=\widehat{H}_{\rm

S}+\widehat{H}_{\rm E}+\widehat{H}_{\rm I}, \end{aligned}$$ (16) where the system Hamiltonain \(\widehat{H}_{\rm S}=\hbar \omega _0{\hat{\sigma }}_z/2\), the environment Hamiltonian

\(\widehat{H}_{\rm E}=\sum _{\vec {k}}\hbar \omega _{\vec {k}}\hat{b}_{\vec {k}}^\dagger \hat{b}_{\vec {k}}\), and the interaction Hamiltonian \(\widehat{H}_{\rm I}={\hat{\sigma }}_z\otimes

\sum _{\vec {k}}\hbar (g_{\vec {k}}\hat{b}_{\vec {k}}^\dagger +g_{\vec {k}}^*\hat{b}_{\vec {k}})\). Assuming that the environment is in a thermal equilibrium state at temperature _T_, then

this model can be analytically solved1 and the qubit dynamics exhibits pure dephasing with the dephasing factor $$\begin{aligned} \phi (t)=\exp [-i\omega _0t-\Phi (t)], \end{aligned}$$ (17)

where \(\Phi (t)=4\int _0^\infty [\mathcal {J}(\omega )/\omega ^2]\coth (\hbar \omega /2k_{\rm B}T)(1-\cos \omega t)d\omega\) incorporates the information for the interaction and the

environmental density of states in terms of the spectral density \(\mathcal {J}(\omega )=\sum _{\vec {k}}|g_{\vec {k}}|^2\delta (\omega -\omega _{\vec {k}})\). In view of Eq. (2), the CHER

of the qubit pure dephasing can be obtained from the inverse Fourier transform $$\begin{aligned} \wp (\omega )=\frac{1}{2\pi }\int _{-\infty }^\infty \phi (t)e^{i\omega t}dt, \end{aligned}$$

(18) with respect to the diagonal member Hamiltonian operators \(\hbar \omega {\hat{\sigma }}_z/2\) in the simulating HE \(\{(\wp (\omega ),\hbar \omega {\hat{\sigma }}_z/2)\}_\omega\).

Note that the effect of \(\omega _0\) is merely to shift \(\wp (\omega )\). Therefore, we can, without loss of generality, assume that \(\omega _0=0\) from this position on. To be a

legitimate probability distribution, the resulting CHER \(\wp (\omega )\) (18) is expected to satisfy the following conditions: * C1 Normalization to unity: \(\int _{-\infty }^\infty \wp

(\omega )d\omega =1\). * C2 Real function: \(\wp (\omega )\in \mathbb {R}, \forall \omega \in \mathbb {R}\). * C3 Positivity: \(\wp (\omega )\ge 0, \forall \omega \in \mathbb {R}\).

Normalization C1 follows straightforwardly from the fact that \(\phi (0)=1\); i.e., \(\int _{-\infty }^\infty \wp (\omega )d\omega =(2\pi )^{-1}\int _{-\infty }^\infty \phi (t)2\pi \delta

(t-0)dt=1\). Since one typically considers the dynamical behaviour of \(\phi (t)\) only for \(t\ge 0\), we can freely extend the time domain to all \(t\in \mathbb {R}\) such that \(\Phi

(t)\) is even and \(\phi (-t)=\phi (t)^*\). Then \(\wp (\omega )=\pi ^{-1}\int _0^\infty \exp [-\Phi (t)]\cos \omega tdt\) is guaranteed to be real, fulfilling condition C2. While conditions

 C1 and C2 are straightforward consequences, it cannot be seen immediately whether the condition C3 is fulfilled by \(\wp (\omega )\) due to the sinusoidally oscillating behaviour of the

integrand in Eq. (18). To prove the positivity of \(\wp (\omega )\) for the qubit pure dephasing reduced from the spin-boson mdoel (16), we turn to Bochner’s theory60 for help. Further

details are given in "Methods". One of our crucial conclusions, the validity of \(\wp (\omega )\), is described as follows: PROPOSITION 1 _Suppose that the qubit pure dephasing

dynamics characterized by_ \(\phi (t)=\exp \left[ -i\omega _0 t-\Phi (t)\right]\) _is CP. There exists a unique Hamiltonian ensemble of diagonal member Hamiltonian operators_ \(\{(\wp

(\omega ),\hbar \omega {\hat{\sigma }}_z/2)\}_\omega\) _which can simulate the system dynamics. Additionally, the CHER_ \(\wp (\omega )=(2\pi )^{-1}\int _{-\infty }^\infty \phi (t)\exp

(i\omega t)dt\) _obtained by the inverse Fourier transform of_ \(\phi (t)\) _is a legitimate probability distribution, satisfying the three conditions for a probability distribution function

that are listed above._ In the following, we consider several heuristic examples of different spectral densities. We have also assumed a degenerate qubit such that \(\omega _0=0\) in these

examples. The resulting \(\wp (\omega )\)’s are therefore centered at \(\omega =0\). Earlier study1 shows that the dephasing factor can be split into the vacuum and thermal contributions as

\(\phi (t)=\exp \left[ -\Phi ^{({\rm vac})}(t)-\Phi ^{({\rm th})}(t)\right]\), where The impact of thermal fluctuations is taken into account by \(\Phi ^{({\rm th})}(t)\). Further detailed

calculations are given in "Methods". We first consider the Ohmic spectral density \(\mathcal {J}_1(\omega )=\omega \exp (-\omega /\omega _{\rm c})\), as shown in the inset of Fig. 

3a, where \(\omega _{\rm c}\) is the cut-off frequency. The dephasing factor is given by $$\begin{aligned} \phi _1(t)=\frac{1}{\left( 1+\omega _{\rm c}^2t^2\right) ^2}\prod _{n=1}^\infty

\left[ 1 +\left( \frac{\omega _{\rm c}k_{\rm B}T}{k_{\rm B}T+n\hbar \omega _{\rm c}}\right) ^2t^2\right] ^{-4}, \end{aligned}$$ (19) with \(k_{\rm B}\) being the Boltzmann constant. It can

be seen that Eq. (19) reproduces the case of zero-temperature limit \(\phi _1(t)=\left( 1+\omega _{\rm c}^2t^2\right) ^{-2}\) as \(T\rightarrow 0\)47. In the case of finite temperature _T_,

the CHER \(\wp _1(\omega )=(2\pi )^{-1}\int _{-\infty }^\infty \phi _1(t)\exp (i\omega t)dt\) can only be calculated numerically. The numerical results are shown in Fig. 3a with \(\omega

_{\rm c}=1\), \(k_{\rm B}/\hbar =1\), and increasing _T_ from 0 to 5 (decreasing opacity). The left panel of Fig. 3a shows the dynamical behaviour of \(\phi _1(t)\). It exhibits a Markovian

pure dephasing as \(\phi _1(t)\) decreases monotonically; meanwhile, as expected, the coherence time decreases with increasing _T_. The right panel of Fig. 3a shows the corresponding \(\wp

_1(\omega )\), which broadens when increasing _T_, reflecting stronger thermal fluctuations. We next consider the family of super-Ohmic spectral densities \(\mathcal {J}_s(\omega )=\eta

\omega ^s\omega ^{1-s}_{\rm c}\exp (-\omega /\omega _{\rm c})\) parameterized by the coupling strength \(\eta\) and the Ohmicity \(s>1\). In the zero-temperature limit, the dephasing

factor is exclusively given by the vacuum contribution \(\phi _s(t)=\exp \left[ -\Phi ^{({\rm vac})}_s(t)\right]\) with $$\begin{aligned} \Phi ^{({\rm vac})}_s(t)=2\eta \Gamma (s-1)\left[

2-\frac{\left( 1+i\omega _{\rm c}t\right) ^{s-1} +\left( 1-i\omega _{\rm c}t\right) ^{s-1}}{\left( 1+\omega _{\rm c}^2t^2\right) ^{s-1}}\right] , \end{aligned}$$ (20) where \(\Gamma (z)\) is

the gamma function. The dynamical behaviours of \(\phi _s(t)\)’s are shown in the left panel of Fig. 3b with \(\eta =1/3\), \(\omega _{\rm c}=1\), and _s_ ranging from 1.5 to 6.5

(decreasing opacity). A transition from Markovianity to non-Markovainity can be seen with increasing _s_. As clearly indicated in the inset, for \(1<s\le 2\) (dashed curves), the qubit

exhibits a Markovian trait as \(\phi _s(t)\)’s decrease monotonically. On the other hand, for \(s>2\) (solid curves), the qubit pure dephasing is definitely non-Markovian due to the

revivals following the initial rapid descents. We stress that the dynamics is always non-Markovian for \(s>2\); however the revivals are negligibly small for \(s>4.5\). These results

are compatible with a previous study 61. The numerical results of \(\wp _s(\omega )\)’s are shown in the right panel of Fig. 3b with increasing Ohmicity _s_ from 1.5 to 6.5 (decreasing

opacity). The aforementioned transition in the dynamical behaviour manifests itself dramatically in terms of the shape of \(\wp _s(\omega )\). Particularly, when _s_ is large, \(\phi _s(t)\)

drops off sharply, therefore the corresponding \(\wp _s(\omega )\) gradually flattens. The underlying reason lies in the fact that the varying of the curvature of \(\phi _s(t)\) will

significantly modulate the shape of its Fourier transform \(\wp _s(\omega )\). In the case of finite temperature _T_, the expression of the dephasing factor \(\phi _s(t)=\exp \left[ -\Phi

_s(t)\right]\) is complicated due to the presence of thermal fluctuations: $$\begin{aligned} \Phi _s(t)= & {} -2\eta \Gamma (s-1)\left[ 2-\frac{\left( 1+i\omega _{\rm c}t\right) ^{s-1}

+\left( 1-i\omega _{\rm c}t\right) ^{s-1}}{\left( 1+\omega _{\rm c}^2t^2\right) ^{s-1}}\right] \nonumber \\&+4\eta \Gamma (s-1)\left( \frac{k_{\rm B}T}{\hbar \omega _{\rm c}}\right)

^{s-1} \left[ 2\zeta \left( s-1,\frac{k_{\rm B}T}{\hbar \omega _{\rm c}}\right) -\zeta \left( s-1,\frac{k_{\rm B}T}{\hbar \omega _{\rm c}}(1+i\omega _{\rm c}t)\right) -\zeta \left(

s-1,\frac{k_{\rm B}T}{\hbar \omega _{\rm c}}(1-i\omega _{\rm c}t)\right) \right] , \end{aligned}$$ (21) where \(\zeta (s,q)=\sum _{n=0}^\infty (q+n)^{-s}\) is the Hurwitz zeta function. The

impact of thermal fluctuations is shown in Fig. 3c with \(\eta =1/3\), \(\omega _{\rm c}=1\), Ohmicity \(s=4\), and increasing _T_ from 0 to 5 (decreasing opacity). In the left panel, the

dynamical behaviour of \(\phi _4(t)\) exhibits a transition from non-Markovianity to Markovianity with increasing _T_, reflecting the fact that the thermal fluctuations will wash out the

memory effect and lead to a Markovian dynamics. The right panel shows the corresponding \(\wp _4(\omega )\), which generically tends to broaden with increasing _T_. However, it is

interesting to note that the aforementioned dynamical transition causes an uneven deformation of \(\wp _4(\omega )\), revealing a competition between non-Markovian memory effect and

Markovian thermal fluctuations. Additionally, by further comparing the three right panels of Fig. 3, we can qualitatively understand that the effects of thermal fluctuations and increasing

_s_ are different, even though they both broaden the CHERs. We have seen several examples of qubit pure dephasing dynamics admitting HE-simulation, i.e., positive CHER. This does not imply

the absence of quantum correlations during the evolution. We stress that the qubit does establish entanglement with its environment62,63,64,65; however, it is not easy to witness its

emergence if the total system evolves autonomously without further manipulation. Consequently, its effects are considered classically in terms of HE-simulation and resulting positive CHER.

On the other hand, given the above examples, one may question the nonexistence of HE-simulation for other types of qubit pure dephasing dynamics. However, to prove the failure of

HE-simulation is, in general, a nontrivial task. In the following, we will study a counterexample of biased spin-boson model leading to CHER showing negative values. NONCLASSICALITY OF

BIASED SPIN-BOSON MODEL The most general form of interaction Hamiltonian leading to qubit pure dephasing is given by $$\begin{aligned} \widehat{H}_{\rm I}=\sum _{j=\uparrow ,\downarrow

}|j\rangle \langle j|\otimes \widehat{B}_j, \end{aligned}$$ (22) where \(\widehat{B}_j\) can be any Hermitian operators acting on the environmental Hilbert space. For the conventional

spin-boson model (16), the environmental operators are taken to be \(\widehat{B}_\uparrow =-\widehat{B}_\downarrow =\sum _{\vec {k}}\hbar (g_{\vec {k}}\hat{b}_{\vec {k}}^\dagger +g_{\vec

{k}}^*\hat{b}_{\vec {k}})\). We slightly generalize the conventional model (16) to a biased one and replace the environmental operators with $$\begin{aligned} \widehat{B}_j=\sum _{\vec

{k}}\hbar (g_{j,\vec {k}}\hat{b}_{\vec {k}}^\dagger +g_{j,\vec {k}}^*\hat{b}_{\vec {k}}). \end{aligned}$$ (23) Note that the coupling constants \(g_{j,\vec {k}}\)’s have _j_-dependence and

would vary with _j_. In the interaction picture (with respect to \(\widehat{H}_{\rm S}+\widehat{H}_{\rm E}\)), the total system evolves according to \(\widehat{U}^{\rm I}(t)=\mathcal

{T}\left\{ \exp \left[ (-i/\hbar )\int _0^t\widehat{H}_{\rm I}(\tau )d\tau \right] \right\}\), where \(\mathcal {T}\) is the time-ordering operator. To investigate the nonclassical effects

caused by the relative phase between the coupling constants, we assume, for simplicity, a balanced condition with finite relative phase, i.e., \(g_{\downarrow ,\vec {k}}=g_{\uparrow ,\vec

{k}}e^{i\varphi }\). This model can also be solved analytically and the qubit pure dephasing is characterized by the dephasing factor $$\begin{aligned} \phi ^{({\rm B})}(t)=\exp \left[

-i\vartheta ^{({\rm B})} (t)-\Phi ^{({\rm B})}(t)\right] , \end{aligned}$$ (24) where \(\vartheta ^{({\rm B})}(t)=2{\rm sign}(t)\sin \varphi \int _0^\infty [\mathcal {J}(\omega )/\omega

^2](1-\cos \omega t)d\omega\) and \(\Phi ^{({\rm B})}(t)=2(1-\cos \varphi )\int _0^\infty [\mathcal {J}(\omega )/\omega ^2]\coth (\hbar \omega /2k_{\rm B}T)(1-\cos \omega t)d\omega\). In the

expression of \(\vartheta ^{({\rm B})}(t)\), we have manually inserted \({\rm sign}(t)\). While this does not affect the pure dephasing dynamics for \(t\ge 0\), it ensures that the property

\(\phi ^{({\rm B})}(-t)=\phi ^{({\rm B})*}(t)\) holds and the CHER \(\wp ^{({\rm B})}(\omega )\) is a real function (condition C2). Details can be found in "Methods". We now

revisit the Ohmic spectral density \(\mathcal {J}_1(\omega )=\omega \exp (-\omega /\omega _{\rm c})\) at finite temperature _T_, where the dephasing factor is given by $$\begin{aligned} \phi

_1^{({\rm B})}(t)=\frac{1}{\left( 1+\omega _{\rm c}^2 t^2\right) ^{(1-\cos \varphi )+i{\rm sign}(t)\sin \varphi }} \prod _{n=1}^\infty \left[ 1+\left( \frac{\omega _{\rm c}k_{\rm

B}T}{k_{\rm B}T +n\hbar \omega _{\rm c}}\right) ^2t^2\right] ^{-2(1-\cos \varphi )}. \end{aligned}$$ (25) The numerical results of the corresponding CHER \(\wp _1^{({\rm B})}(\omega )=(2\pi

)^{-1}\int _{-\infty }^\infty \phi _1^{({\rm B})}(t)\exp (i\omega t)dt\) are shown in Fig. 4 with \(\omega _{\rm c}=1\), \(k_{\rm B}/\hbar =1\), and an increasing _T_ from 0 to 2 (decreasing

opacity). In the left (\(\varphi =2\pi /4\)) and middle (\(\varphi =3\pi /4\)) panels of Fig. 4, we can see a shallow, and stretched, negative wing for each curve. The insets further zoom

in to the negative wings. This is a signature of the nonclassical trait of this biased model, clearly indicating the emergence of nonclassical correlations between the qubit and it

environment. As _T_ increases from 0 to 2 (decreasing opacity), the negative wing gradually fades away and the CHER becomes broader and lower, in line with the usual intuition that the

thermal fluctuations are detrimental to quantum nature. On the other hand, for the case of \(\varphi =\pi\), all the formulae reduce to the conventional ones; consequently, the CHER for

\(\varphi =\pi\) is positive and the right panel of Fig. 4 reproduces the one of Fig. 3. UNIQUENESS OF CHER FOR PURE DEPHASING Through the above examples, one may be convinced of the

uniqueness of the CHER for qubit pure dephasing, as \(\wp (\omega )\) is obtained from the Fourier inverse transform of dephasing factor \(\phi (t)\) via Eq. (18). Nevertheless, whenever one

considers the case of higher dimensional pure dephasing, this becomes problematic as Eq. (18) is never applicable for higher dimensional cases. In fact, the uniqueness still holds, with

respect to diagonal member Hamiltonian operators, even if one considers the case of any dimensional pure dephasing. More precisely, it has been proven48 that, given any dimensional pure

dephasing, there exists a unique CHER, encapsulated within a HE of diagonal member Hamiltonian operators, satisfying Eq. (12). The spirit of the proof is based on the abelian nature of

diagonal member Hamiltonian operators in the HE and provides further insights into the algebraic structure behind the CHER. The Fourier transform in Eq. (2) integrates over full real

numbers, which forms an abelian group with respect to multiplication. However, the unitary group generated by Hermitian operators fails to be abelian. This renders the general solution to

Eq. (12) highly nontrivial. Therefore, the closely related problem of random-unitary decomposition can only be tackled numerically 66. To circumvent this issue, we may restrict ourselves to

an abelian one. Accordingly, if we consider the group \(\mathcal {G}\) in Eq. (12) to be generated by a maximally abelian subalgebra, i.e., the Cartan subalgebra of \(\mathfrak {su}(n)\),

then several intuitive algebraic properties are inherited from the conventional Fourier transform, including the one-to-one correspondence between \(\wp\) and \(\mathcal {E}_t\).

Consequently, under the framework of Cartan subalgebra, we can explicitly deal with the bijective correspondence between pure dephasing and the CHER with respect to diagonal member

Hamiltonian operators. In other words, the uniqueness of CHER for pure dephasing straightforwardly follows, with respect to diagonal member Hamiltonian operators. MULTIPLE REPRESENTATIONS

FOR UNITAL DYNAMICS Based on the above algebraic insights into the CHER, it is straightforward to deduce the breakdown of the uniqueness of the CHER whenever one goes beyond pure dephasing.

To examine this, we explain how to construct multiple \(\wp\) satisfying Eq. (12) simultaneously for a given qubit unital dynamics \(\mathcal {E}_t\), which may either result theoretically

from solving certain master equation or experimentally from process tomography raw data. Since now we are working with \(\mathfrak {u}(2)=\mathfrak {u}(1)\oplus \mathfrak {su}(2)\), the

generators are explicitly chosen to be identity \(\widehat{I}\) and Pauli matrices \({\hat{\sigma }}_j\). The matrix elements of the dynamical linear map \(\mathcal {E}_t^{(\tilde{\sigma

})}\) on the left hand side of Eq. (12) are determined according to $$\begin{aligned} \left[ \mathcal {E}_t^{(\tilde{\sigma })}\right] _{j,k}= \frac{1}{2}{\rm Tr}\left[ {\hat{\sigma

}}_j\cdot \mathcal {E}_t\{{\hat{\sigma }}_k\}\right] . \end{aligned}$$ (26) On the other hand, according to the commutation relation \([{\hat{\sigma }}_j,{\hat{\sigma }}_k]=\varepsilon

_{jkl}i2{\hat{\sigma }}_l\), the Pauli matrices in the adjoint representation are written as $$\begin{aligned} \tilde{\sigma }_x=\left[ \begin{array}{c|ccc} 0 &{} 0 &{} 0 &{} 0

\\ \hline 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -i2\\ 0 &{} 0 &{} i2&{} 0 \end{array} \right] , \tilde{\sigma }_y=\left[ \begin{array}{c|ccc} 0 &{}

0 &{} 0 &{} 0 \\ \hline 0 &{} 0 &{} 0 &{} i2 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -i2&{} 0 &{} 0 \end{array} \right] , \tilde{\sigma }_z=\left[

\begin{array}{c|ccc} 0 &{} 0 &{} 0 &{} 0 \\ \hline 0 &{} 0 &{}-i2&{} 0 \\ 0 &{} i2&{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \end{array} \right] .

\end{aligned}$$ (27) Note that \(\widetilde{I}=0\) as \([\widehat{I},{\hat{\sigma }}_j]=0\), \(\forall ~j\). For any \(\widehat{H}_\lambda =(\lambda _0\widehat{I}+\varvec{\lambda }\cdot

\hat{\varvec{\sigma }})/2\in \mathfrak {u}(2)\), its adjoint representation reads $$\begin{aligned} \widetilde{H}_\lambda =(\varvec{\lambda }\cdot \tilde{\varvec{\sigma }})/2=\left[

\begin{array}{c|ccc} 0 &{} 0 &{} 0 &{} 0 \\ \hline 0 &{} 0 &{} -i\lambda _z &{} i\lambda _y \\ 0 &{} i\lambda _z &{} 0 &{} -i\lambda _x\\ 0 &{}

-i\lambda _y &{} i\lambda _x&{} 0 \end{array} \right] . \end{aligned}$$ (28) Then the unitary operator in the adjoint representation on the right hand side of Eq. (12) can be

expressed as $$\begin{aligned} e^{-i(\varvec{\lambda }\cdot \tilde{\varvec{\sigma }}t)/2}=\left[ \begin{array}{c|ccc} 1 &{} 0 &{} 0 &{} 0 \\ \hline 0 &{} &{} &{} \\ 0

&{} &{} \widetilde{\mathcal {U}}_t &{} \\ 0 &{} &{} &{} \\ \end{array}\right] , \end{aligned}$$ (29) where \(\widetilde{\mathcal {U}}_t\) is a \(3\times 3\)

orthogonal matrix. Its elements are given in "Methods" with the change of parameters to spherical coordinate \(\lambda _x=\omega \sin \theta \cos \psi\), \(\lambda _y=\omega \sin

\theta \sin \psi\), and \(\lambda _z=\omega \cos \theta\). After determining the matrix elements on both sides, Eq. (12) implies 9 equations governing \(\wp (\omega ,\theta ,\psi )\):

$$\begin{aligned} \left[ \mathcal {E}_t^{(\tilde{\sigma })}\right] _{j,k}=\int \int _0^\infty \wp (\omega ,\theta ,\psi )\left[ \widetilde{\mathcal {U}}_t\right] _{j,k}\omega ^2 d\omega

d\Omega . \end{aligned}$$ (30) As shown in "Methods", each \(\left[ \widetilde{\mathcal {U}}_t\right] _{j,k}\) can also be expanded in terms of spherical harmonics \({\rm

Y}_{l,m}(\theta ,\psi )\) in real form with \(l\le 2\). We can therefore expand \(\wp (\omega ,\theta ,\psi )\) as well and divide the expansion into two types according to the index _l_

$$\begin{aligned} \wp (\omega ,\theta ,\psi )=\sum _{l\le 2,m}\wp _{l,m}(\omega ){\rm Y}_{l,m}(\theta ,\psi ) +\sum _{l\ge 3,m}\wp _{l,m}(\omega ){\rm Y}_{l,m}(\theta ,\psi ).

\end{aligned}$$ (31) There are 9 terms in the first type with \(l\le 2\); therefore \(\wp _{l,m}(\omega )\) can be solved with Eq. (30). On the other hand, the second type with \(l\ge 3\)

has no contribution to Eq. (30) due to the orthogonality of \({\rm Y}_{l,m}(\theta ,\psi )\). These observations also imply that, if two CHERs only differ in the second type with \(l\ge 3\),

i.e., \(\wp _1-\wp _2=\sum _{l\ge 3,m}\Delta \wp _{l,m}(\omega ){\rm Y}_{l,m}(\theta ,\psi )\), then the two CHERs simultaneously satisfy Eq. (30), as well as Eq. (12). Consequently, we can

draw the conclusion of the breakdown of the uniqueness of the CHER beyond pure dephasing. EXPERIMENTAL PROPOSAL Finally, in order to underpin the practical viability of the CHER theory,

here we present a promising experimental proposal based upon free induction decay (FID) measurement of the negatively charged nitrogen-vacancy (NV\(^{-}\)) center in a diamond67,68,69. The

NV\(^{-}\) center has an electron spin-1 triplet as its ground states, with a zero-field splitting \(D=2.87\) GHz between \(m_{\rm S}=0\) and \(m_{\rm S}=\pm 1\). The degeneracy between

\(m_{\rm S}=\pm 1\) can be lifted by applying an external magnetic field, allowing selective microwave (MW) excitation of a single spin transition \(|0\rangle \leftrightarrow |1\rangle\) and

forming a logical qubit. Due to strong binding between carbon atoms in the diamond lattice, the electron spin coherence time is not limited by the spin-lattice interactions. Therefore, many

interesting quantum effects can be observed even at room temperature. Rather, the spin qubit operation is subjected to noise mainly from the nuclear spin bath formed by the \(^{13}\)C

isotope (1.1\(\%\) natural abundance), leading to a spin qubit relaxation time \(T_1\) in the order of milliseconds70,71 and a dephasing time \(T_2^*\) of microseconds72,73. Several

techniques have been developed for prolonging the coherence time, e.g., isotopic purification74 and nuclear spin polarization75,76. To experimentally reconstruct the dynamical linear map

\(\mathcal {E}_t^{(\widehat{L})}\) in Eq. (12), one should, in principle, perform the quantum process tomography experiment to gather necessary information on the qubit dynamics.

Fortunately, due to the three-order difference between \(T_1\) and \(T_2^*\), as well as the unique optical properties of the NV\(^{-}\) center, the qubit dynamics can be well approximated

by pure dephasing. Meanwhile, an appropriate variation of the standard Ramsey pulse sequence shown in Fig. 5 is sufficient for our purpose, circumventing the burden of performing the

standard quantum process tomography experiment. Figure 5a shows the standard Ramsey pulse sequence, beginning with an electron spin initialization to \(|0\rangle\) by a 532-nm green laser. A

successive MW \((\pi /2)_x\) pulse creates a superposition state and, consequently, turns on the interaction with the nuclear spin bath. The qubit will then undergo an FID process for a

period (FID time). The second MW \((\pi /2)_x\) pulse converts the phase information into population. The final 532-nm green laser pumping is used to detect the remaining population in the

\(|0\rangle\) state and the signal is recorded as the normalized fluorescence \({\rm I}_x(t)\). To completely reconstruct the phase information, an additional measurement is necessary. As

shown in Fig. 5b, the second MW pulse is replaced by \((\pi /2)_y\) to extract the phase information along the other orthogonal axis and the signal is recorded as \({\rm I}_y(t)\). The

dephasing factor is then determined by the two measured fluorescence signals according to $$\begin{aligned} \phi (t)=-\left[ 2{\rm I}_x(t)-1\right] +i\left[ 2{\rm I}_y(t)-1\right] .

\end{aligned}$$ (32) The Fourier transform (18) leads to the resulting \(\wp (\omega )\). We stress that this proposed experimental setup is fully compatible with present-day techniques.

Finally, it is worth noting that, the entanglement between the electron spin and its \(^{13}\)C nuclear spin bath established during the FID procedure can be detected with local operations

focussing exclusively on the electron spin65. This locally detectable entanglement constitutes the origin of nonclassicality in the CHER theory. Our experimental proposal provides further

protocol to estimate the presence of the entanglement. DISCUSSIONS AND CONCLUSION In summary, we have elaborated the theoretical foundation for the notion of CHER within a unified framework

in detail, as well as its geometrical interpretation in terms of random phase model. Through the Fourier transform on group formalism, it is clearer that CHER plays the role of being the

representation of a unital dynamics in the frequency domain. Meanwhile, along with the investigation into the system–environment correlations, we have also discussed its capability of

characterizing the nonclassical treats of dephasing dynamics. Nonclassical distribution over phase space for a state is extensively studied, particularly in the field of quantum optics with

the Wigner function40 or the Glauber-Sudarshan _P_ representation41,42. It should be pointed out that similar notion of process nonclassicality has attracted increasing research interests

and alternative definitions based on monitoring certain nonclassical traits of the states have been discussed77,78,79,80 in recent years. Nevertheless, rather than a specified quantum state,

we focus on the dynamical processes. More insights can be provided with some further comparative studies. With several examples, we have also shown generically that the increasing

environmental temperature will broaden the CHERs and diminish the nonclassical traits. This is in agreement with the common intuition that the thermal fluctuations are detrimental to the

quantum nature. Additionally, we have also demonstrated the transition between Markovianity and non-Markovianity by varying the Ohmicity of the spectral density and the environmental

temperature. It is known that non-Markovianity may result from statistical mixture of random unitary50,66,81,82 or, more generally, some other dynamical processes83,84. Our results suggest

that there are discrepancies between the nonclassicality and non-Markovianity, which raise the question of the true quantum non-Markovianity85. Notably, as the aforementioned transition

phenomenon is even manifest from the shape of CHERs, this may stimulate the development of the techniques of probe for the properties of ambient environments86,87,88,89,90. Furthermore, we

have also discussed the uniqueness of CHER for pure dephasing with respect to the Cartan subslgebra of \(\mathfrak {su}(n)\). However, when going beyond pure dephasing, the uniqueness breaks

down as a result of the analysis on the underlying algebraic structure. To explicitly show the breakdown of uniqueness and explain how to construct multiple CHER beyond pure dephasing, we

have considered a general unital dynamics. If two CHERs only differ in the spherical harmonics of an order larger than 3 (\(l\ge 3\)), the two CHERs represent the same unital dynamics.

Interestingly, the question of how to define a principal one among multiple CHERs for unital dynamics can be intriguing. These unresolved points could be seminal and stimulate further

studies from many different aspects in the future. Finally, we have also proposed a promising experimental setup to explain how to realize our CHER theory with measured signals. As the

NV\(^-\) center possesses several prominent properties and can work under ambient conditions, many techniques have been extensively developed. Therefore, the NV\(^-\) center is widely

adopted as the testbed of fundamental quantum physics and advanced quantum technologies, e.g., Refs.91,92,93. We propose to utilize this mature platform, along with an appropriate variation

of the pulse sequence, and elucidate how to reconstruct the dephasing factor \(\phi (t)\) and the resulting CHER \(\wp (\omega )\) from the measured fluorescence signals \({\rm I}_x(t)\) and

\({\rm I}_y(t)\). METHODS BOCHNER’S THEOREM To prove Proposition 1 in the main text, we need to utilize several mathematical supplements, including the Bochner’s theorem60. We first recall

the definition of positive definiteness: DEFINITION 2 A function \(f:\mathbb {R}\rightarrow \mathbb {C}\) is called to be positive definite if it satisfies $$\begin{aligned} \sum

_{j,k}f\left( t_j-t_k\right) z_jz_k^*\ge 0 \end{aligned}$$ (33) for any finite number of pairs \(\{(t_j,z_j)|t_j\in \mathbb {R},z_j\in \mathbb {C}\}\). We stress that the notion of positive

definiteness is very different from a positive function since a positive function may not necessarily be positive definite and _vice versa_. Instead, it is equivalent to the positive

semidefiniteness of an Hermitian matrix \(\left[ f(t_j-t_k)\right] _{j,k\in \mathcal {S}}\) formed by collecting function values \(f(t_j-t_k)\) in accordance with certain set of indices

\(\mathcal {S}\). Particularly, the function _f_ in Definition 2 can even be complex. We then find that \(\phi (t)\) in Eq. (17) is positive definite47, as stated in the following lemma:

LEMMA 3 _Suppose that the dephasing factor_ (17) _defines a CP qubit pure dephasing dynamics. If we further assume that_ \(\Phi (t)\) _is even and_ \(\phi (-t)=\phi (t)^*\), _then_ \(\phi

(t)\) _defined on_ \(\mathbb {R}\) _is positive definite._ Now we are ready to introduce the Bochner’s theorem. The following expression facilitates our sequential discussions: THEOREM 4

(Bochner’s theorem) _A function_ \(f:\mathbb {R}\rightarrow \mathbb {C}\) _is the Fourier transform of unique positive measure with density function_ \(\wp\) _if and only if_ _f_ _is

continuous and positive definite._ Combining above, we can conclude that \(\phi (t)\) in Eq. (17) is positive definite and, consequently, is the Fourier transform of certain legitimate

probability distribution \(\wp (\omega )\), an analog to that in Eq. (2). These results are summarized in Proposition 1 in the main text. VACUUM AND THERMAL CONTRIBUTIONS TO THE DEPHASING

FACTOR As discussed in the main text, the qubit pure dephasing reduced from the spin-boson mdoel (16) is characterized by the dephasing factor \(\phi (t)=\exp [-i\omega _0t-\Phi (t)]\) with

\(\Phi (t)=4\int _0^\infty [\mathcal {J}(\omega )/\omega ^2]\coth (\hbar \omega /2k_{\rm B}T)(1-\cos \omega t)d\omega\). It is convenient to split it into the vacuum and thermal parts1 as

\(\Phi (t)=\Phi ^{({\rm vac})}(t)+\Phi ^{({\rm th})}(t)\), where $$\begin{aligned} \Phi ^{({\rm vac})}(t)=4\int _0^\infty \frac{\mathcal {J}(\omega )}{\omega ^2}(1-\cos \omega t)d\omega

\end{aligned}$$ (34) and $$\begin{aligned} \Phi ^{({\rm th})}(t)=4\int _0^\infty \frac{\mathcal {J}(\omega )}{\omega ^2}\left[ \coth \left( \frac{\hbar \omega }{2k_{\rm B}T}\right) -1\right]

(1-\cos \omega t)d\omega . \end{aligned}$$ (35) It can be seen that \(\Phi ^{({\rm vac})}(t)\) is independent of temperature and corresponds to the contribution in the zero-temperature

limit. The impact of thermal fluctuations is taken into account by the thermal contribution \(\Phi ^{({\rm th})}(t)\). OHMIC SPECTRAL DENSITY Considering the case of Ohmic spectral density

\(\mathcal {J}_1(\omega )=\omega \exp (-\omega /\omega _{\rm c})\), the vacuum contribution (34) can be obtained with the help of series expansion as $$\begin{aligned} \Phi _1^{({\rm

vac})}(t)= & {} 4\int _0^\infty \frac{1-\cos \omega t}{\omega }e^{-\frac{\omega }{\omega _{\rm c}}}d\omega \nonumber \\= & {} 4\sum _{n=1}^\infty \int _0^\infty

\frac{(-1)^{n-1}}{2n!}\omega ^{2n-1}t^{2n}e^{-\frac{\omega }{\omega _{\rm c}}}d\omega \nonumber \\= & {} 4\sum _{n=1}^\infty \frac{(-1)^{n-1}}{2n}\omega _{\rm c}^{2n}t^{2n}=2\ln \left(

1+\omega _{\rm c}^2t^2\right) . \end{aligned}$$ (36) With the help of the expansion \(\coth x=1+2\sum _{n=1}^\infty \exp (-2nx)\), the thermal contribution (35) can be easily obtained in a

similar manner: $$\begin{aligned} \Phi _1^{({\rm th})}(t)= & {} 4\int _0^\infty \frac{1-\cos \omega t}{\omega }e^{-\frac{\omega }{\omega _{\rm c}}}\left[ \coth \left( \frac{\hbar \omega

}{2k_{\rm B}T}\right) -1\right] d\omega =\sum _{n=1}^\infty 4\int _0^\infty \frac{1-\cos \omega t}{\omega }2e^{-\left( \frac{1}{\omega _{\rm c}}+\frac{n\hbar }{k_{\rm B}T}\right) \omega

}d\omega \nonumber \\= & {} 4\sum _{n=1}^\infty \ln \left[ 1+\left( \frac{\omega _{\rm c}k_{\rm B}T}{k_{\rm B}T+n\hbar \omega _{\rm c}}\right) ^2t^2\right] . \end{aligned}$$ (37) Then

the dephasing factor is given by \(\phi _1(t)=\exp [-\Phi _1^{({\rm vac})}(t)-\Phi _1^{({\rm th})}(t)]\). This reproduces Eq. (19) in the main text. FAMILY OF SUPER-OHMIC SPECTRAL DENSITIES

In the example of super-Ohmic spectral densities \(\mathcal {J}_s(\omega )=\eta \omega ^s\omega ^{1-s}_{\rm c}\exp (-\omega /\omega _{\rm c})\), the vacuum part can be split into three

terms: $$\begin{aligned} \Phi _s^{({\rm vac})}(t)= & {} 4\int _0^\infty \eta \frac{\omega ^{s-2}}{\omega ^{s-1}_{\rm c}}(1-\cos \omega t)e^{-\frac{\omega }{\omega _{\rm c}}}d\omega

\nonumber \\= & {} 4\eta \int _0^\infty \frac{\omega ^{s-2}}{\omega ^{s-1}_{\rm c}}e^{-\frac{\omega }{\omega _{\rm c}}}d\omega -2\eta \int _0^\infty \frac{\omega ^{s-2}}{\omega

^{s-1}_{\rm c}}e^{-i\omega t} e^{-\frac{\omega }{\omega _{\rm c}}}d\omega -2\eta \int _0^\infty \frac{\omega ^{s-2}}{\omega ^{s-1}_{\rm c}}e^{i\omega t} e^{-\frac{\omega }{\omega _{\rm

c}}}d\omega . \end{aligned}$$ (38) Then, along with the definition of gamma function \(\Gamma (s+1)=\int _0^\infty x^s \exp (-x)dx\) and usual calculation, one can obtain Eq. (20) in the

main text. In the case of finite temperature _T_, the thermal part is present and written as $$\begin{aligned} \Phi _s^{({\rm th})}(t)=4\int _0^\infty \eta \frac{\omega ^{s-2}}{\omega

^{s-1}_{\rm c}}(1-\cos \omega t)e^{-\frac{\omega }{\omega _{\rm c}}} \left[ \coth \left( \frac{\hbar \omega }{2k_{\rm B}T}\right) -1\right] d\omega . \end{aligned}$$ (39) By using similar

approaches, one can obtain $$\begin{aligned} \Phi _s^{({\rm th})}(t)= & {} 4\eta \sum _{n=1}^\infty \int _0^\infty \frac{\omega ^{s-2}}{\omega ^{s-1}_{\rm c}}(2-e^{-i\omega t}-e^{i\omega

t}) e^{-\left( \frac{1}{\omega _{\rm c}}+\frac{n\hbar }{k_{\rm B}T}\right) \omega }d\omega \nonumber \\= & {} 4\eta \sum _{n=1}^\infty \Gamma (s-1) \left[ \frac{2}{\left( 1+n\frac{\hbar

\omega _{\rm c}}{k_{\rm B}T}\right) ^{s-1}}-\frac{1}{\left( 1+n\frac{\hbar \omega _{\rm c}}{k_{\rm B}T}+i\omega _{\rm c}t\right) ^{s-1}} -\frac{1}{\left( 1+n\frac{\hbar \omega _{\rm

c}}{k_{\rm B}T}-i\omega _{\rm c}t\right) ^{s-1}}\right] \nonumber \\= & {} -4\eta \Gamma (s-1)\left[ 2-\frac{\left( 1+i\omega _{\rm c}t\right) ^{s-1}+\left( 1-i\omega _{\rm c}t\right)

^{s-1}}{\left( 1+\omega _{\rm c}^2t^2\right) ^{s-1}}\right] \nonumber \\&+4\eta \Gamma (s-1)\left( \frac{k_{\rm B}T}{\hbar \omega _{\rm c}}\right) ^{s-1}\left[ 2\zeta \left(

s-1,\frac{k_{\rm B}T}{\hbar \omega _{\rm c}}\right) -\zeta \left( s-1,\frac{k_{\rm B}T}{\hbar \omega _{\rm c}}(1+i\omega _{\rm c}t)\right) -\zeta \left( s-1,\frac{k_{\rm B}T}{\hbar \omega

_{\rm c}}(1-i\omega _{\rm c}t)\right) \right] , \nonumber \\ \end{aligned}$$ (40) where \(\zeta (s,q)=\sum _{n=0}^\infty (q+n)^{-s}\) is the Hurwitz zeta function. Then Eq. (21) is given by

\(\Phi _s(t)=\Phi _s^{({\rm vac})}(t)+\Phi _s^{({\rm th})}(t)\). BIASED SPIN-BOSON MODEL We proceed to the biased spin-boson model with interaction Hamiltonian given by Eqs. (22) and (23).

In the interaction picture with respect to \(\widehat{H}_{\rm S}+\widehat{H}_{\rm E}\), it is written as $$\begin{aligned} \widehat{H}_{\rm I}(t)=\sum _{j=\uparrow ,\downarrow }|j\rangle

\langle j|\otimes \widehat{B}_j^{{\rm I}}(t), \end{aligned}$$ (41) where $$\begin{aligned} \widehat{B}_j^{{\rm I}}(t)=\sum _{\vec {k}}\hbar (g_{j,\vec {k}}\hat{b}_{\vec {k}}^\dagger

e^{i\omega _{\vec {k}} t} +g_{j,\vec {k}}^*\hat{b}_{\vec {k}}e^{-i\omega _{\vec {k}} t}). \end{aligned}$$ (42) Note that the interaction Hamiltonian do not commute to each other at different

time: $$\begin{aligned} \left[ \widehat{H}_{\rm I}(\tau ),\widehat{H}_{\rm I}(\tau ^\prime )\right] =\sum _{j=\uparrow ,\downarrow }|j\rangle \langle j|\otimes \sum _{\vec {k}}-i2\hbar

^2|g_{j,\vec {k}}|^2\sin \omega _{\vec {k}}\left( \tau -\tau ^\prime \right) . \end{aligned}$$ (43) Then the time-ordering \(\mathcal {T}\) in the unitary evolution operator

\(\widehat{U}^{\rm I}(t)=\mathcal {T}\left\{ \exp \left[ (-i/\hbar )\int _0^t\widehat{H}_{\rm I}(\tau )d\tau \right] \right\}\) will play a significant role1: $$\begin{aligned}

\widehat{U}^{\rm I}(t)= & {} \exp \left[ -\frac{1}{2\hbar ^2}\int _0^t\int _0^\tau [\widehat{H}_{\rm I}(\tau ),\widehat{H}_{\rm I}(\tau ^\prime )]d\tau ^\prime d\tau \right] \exp \left[

-\frac{i}{\hbar }\int _0^t\widehat{H}_{\rm I}(\tau )d\tau \right] \nonumber \\= & {} \sum _{j=\uparrow ,\downarrow }|j\rangle \langle j|\otimes \prod _{\vec {k}}\exp \left[ i|g_{j,\vec

{k}}|^2\frac{\omega _{\vec {k}}t-\sin \omega _{\vec {k}}t}{\omega _{\vec {k}}^2}\right] \widehat{D}[g_{j,\vec {k}}\alpha _{\vec {k}}(t)], \end{aligned}$$ (44) where \(\widehat{D}[g_{j,\vec

{k}}\alpha _{\vec {k}}(t)]=\exp [g_{j,\vec {k}}\alpha _{\vec {k}}(t)\hat{b}_{\vec {k}}^\dagger -g_{j,\vec {k}}^*\alpha _{\vec {k}}^*(t)\hat{b}_{\vec {k}}]\) is the displacement operator and

\(\alpha _{\vec {k}}(t)=(1-e^{i\omega _{\vec {k}}t})/\omega _{\vec {k}}\). Now we assume that the initial state \(\rho _{\rm T}(0)=\rho _{\rm S}(0)\otimes \rho _{\rm E}(0)\) with \(\rho

_{\rm E}(0)=\exp [-\widehat{H}_{\rm E}/k_{\rm B}T]/Z\) being an equilibrium state at temperature _T_. Along with the two prescriptions \(\widehat{D}[\alpha ]\widehat{D}[\beta ]=\exp [(\alpha

\beta ^*-\alpha ^*\beta )/2]\widehat{D}[\alpha +\beta ]\) and \(\langle \widehat{D}[\alpha ]\rangle =\exp [-\coth (\hbar \omega /2k_{\rm B}T)|\alpha |^2/2]\), the qubit pure dephasing is

characterized by the dephasing factor $$\begin{aligned} \phi ^{({\rm B})}(t)= & {} \left\langle \prod _{\vec {k}}\exp \left[ -i|g_{\downarrow ,\vec {k}}|^2\frac{\omega _{\vec {k}}t-\sin

\omega _{\vec {k}}t}{\omega _{\vec {k}}^2}\right] \widehat{D}[-g_{\downarrow ,\vec {k}}\alpha _{\vec {k}}(t)] \prod _{\vec {k}}\exp \left[ i|g_{\uparrow ,\vec {k}}|^2\frac{\omega _{\vec

{k}}t-\sin \omega _{\vec {k}}t}{\omega _{\vec {k}}^2}\right] \widehat{D}[g_{\uparrow ,\vec {k}}\alpha _{\vec {k}}(t)]\right\rangle \nonumber \\= & {} \left\langle \prod _{\vec {k}}\exp

\left[ -i|g_{\downarrow ,\vec {k}}|^2\frac{\omega _{\vec {k}}t-\sin \omega _{\vec {k}}t}{\omega _{\vec {k}}^2}\right] \exp \left[ i|g_{\uparrow ,\vec {k}}|^2\frac{\omega _{\vec {k}}t-\sin

\omega _{\vec {k}}t}{\omega _{\vec {k}}^2}\right] \right. \nonumber \\&\times \left. \exp \left[ -(g_{\downarrow ,\vec {k}}g_{\uparrow ,\vec {k}}^*-g_{\downarrow ,\vec {k}}^*g_{\uparrow

,\vec {k}})\frac{1-\cos \omega _{\vec {k}}t}{\omega _{\vec {k}}^2}\right] \widehat{D}[(g_{\uparrow ,\vec {k}}-g_{\downarrow ,\vec {k}})\alpha _{\vec {k}}(t)] \right\rangle . \end{aligned}$$

(45) In the main text, we have assumed the balanced condition with finite relative phase, \(g_{\downarrow ,\vec {k}}=g_{\uparrow ,\vec {k}}e^{i\varphi }\). Then the expression of \(\phi

^{({\rm B})}(t)\) can be significantly simplified. Along with the definition of spectral density, \(\mathcal {J}(\omega )=\sum _{\vec {k}}|g_{\vec {k}}|^2\delta (\omega -\omega _{\vec

{k}})\), we arrive the desired result: $$\begin{aligned} \phi ^{({\rm B})}(t)=\exp \left[ -i\vartheta ^{({\rm B})}(t)-\Phi ^{({\rm B})}(t)\right] , \end{aligned}$$ (46) where \(\vartheta

^{({\rm B})}(t)=2{\rm sign}(t)\sin \varphi \int _0^\infty [\mathcal {J}(\omega )/\omega ^2](1-\cos \omega t)d\omega\) and \(\Phi ^{({\rm B})}(t)=2(1-\cos \varphi )\int _0^\infty [\mathcal

{J}(\omega )/\omega ^2]\coth (\hbar \omega /2k_{\rm B}T)(1-\cos \omega t)d\omega\). THE UNITARY OPERATOR IN THE ADJOINT REPRESENTATION The adjoint representation of the unitary operator in

Eq. (29) is a \(4\times 4\) matrix. However, as we consider qubit unital dynamics, it is of block-diagonalized form with a nontrivial \(3\times 3\) block \(\widetilde{\mathcal {U}}_t\). Note

that \(\widetilde{\mathcal {U}}_t\) is a orthogonal matrix generated by \(\tilde{\sigma }_j\). Below we explicitly show the matrix elements with the change of parameters to spherical

coordinate. Furthermore, each of them can be expanded in terms of spherical harmonics \({\rm Y}_{l,m}(\theta ,\psi )\) in real form with \(l\le 2\). $$\begin{aligned} \left[

\widetilde{\mathcal {U}}_t\right] _{11}= & {} \sin ^2\theta \cos ^2\psi +\left( \sin ^2\theta \sin ^2\psi +\cos ^2\theta \right) \cos \omega t \nonumber \\= & {} \frac{\sqrt{4\pi

}}{3}{\rm Y}_{0,0}-\sqrt{\frac{4\pi }{45}}{\rm Y}_{2,0}+\sqrt{\frac{4\pi }{15}}{\rm Y}_{2,2} +\left( \frac{\sqrt{16\pi }}{3}{\rm Y}_{0,0}+\sqrt{\frac{4\pi }{45}}{\rm

Y}_{2,0}-\sqrt{\frac{4\pi }{15}}{\rm Y}_{2,2}\right) \cos \omega t, \end{aligned}$$ (47) $$\begin{aligned} \left[ \widetilde{\mathcal {U}}_t\right] _{21}= & {} \sin ^2\theta \sin \psi

\cos \psi (1-\cos \omega t)+\cos \theta \sin \omega t \nonumber \\= & {} \sqrt{\frac{4\pi }{15}}{\rm Y}_{2,-2}(1-\cos \omega t)+\sqrt{\frac{4\pi }{3}}{\rm Y}_{1,0}\sin \omega t,

\end{aligned}$$ (48) $$\begin{aligned} \left[ \widetilde{\mathcal {U}}_t\right] _{31}= & {} \sin \theta \cos \theta \cos \psi (1-\cos \omega t)-\sin \theta \sin \psi \sin \omega t

\nonumber \\= & {} \sqrt{\frac{4\pi }{15}}{\rm Y}_{2,1}(1-\cos \omega t)-\sqrt{\frac{4\pi }{3}}{\rm Y}_{1,-1}\sin \omega t, \end{aligned}$$ (49) $$\begin{aligned} \left[

\widetilde{\mathcal {U}}_t\right] _{12}= & {} \sin ^2\theta \sin \psi \cos \psi (1-\cos \omega t)-\cos \theta \sin \omega t \nonumber \\= & {} \sqrt{\frac{4\pi }{15}}{\rm

Y}_{2,-2}(1-\cos \omega t)-\sqrt{\frac{4\pi }{3}}{\rm Y}_{1,0}\sin \omega t, \end{aligned}$$ (50) $$\begin{aligned} \left[ \widetilde{\mathcal {U}}_t\right] _{22}= & {} \sin ^2\theta

\sin ^2\psi +\left( \sin ^2\theta \cos ^2\psi +\cos ^2\theta \right) \cos \omega t \nonumber \\= & {} \frac{\sqrt{4\pi }}{3}{\rm Y}_{0,0}-\sqrt{\frac{4\pi }{45}}{\rm

Y}_{2,0}-\sqrt{\frac{4\pi }{15}}{\rm Y}_{2,2} +\left( \frac{\sqrt{16\pi }}{3}{\rm Y}_{0,0}+\sqrt{\frac{4\pi }{45}}{\rm Y}_{2,0}+\sqrt{\frac{4\pi }{15}}{\rm Y}_{2,2}\right) \cos \omega t,

\end{aligned}$$ (51) $$\begin{aligned} \left[ \widetilde{\mathcal {U}}_t\right] _{32}= & {} \sin \theta \cos \theta \sin \psi (1-\cos \omega t)+\sin \theta \cos \psi \sin \omega t

\nonumber \\= & {} \sqrt{\frac{4\pi }{15}}{\rm Y}_{2,-1}(1-\cos \omega t)+\sqrt{\frac{4\pi }{3}}{\rm Y}_{1,1}\sin \omega t, \end{aligned}$$ (52) $$\begin{aligned} \left[

\widetilde{\mathcal {U}}_t\right] _{13}= & {} \sin \theta \cos \theta \cos \psi (1-\cos \omega t)+\sin \theta \sin \psi \sin \omega t \nonumber \\= & {} \sqrt{\frac{4\pi }{15}}{\rm

Y}_{2,1}(1-\cos \omega t)+\sqrt{\frac{4\pi }{3}}{\rm Y}_{1,-1}\sin \omega t, \end{aligned}$$ (53) $$\begin{aligned} \left[ \widetilde{\mathcal {U}}_t\right] _{23}= & {} \sin \theta \cos

\theta \sin \psi (1-\cos \omega t)-\sin \theta \cos \psi \sin \omega t \nonumber \\= & {} \sqrt{\frac{4\pi }{15}}{\rm Y}_{2,-1}(1-\cos \omega t)-\sqrt{\frac{4\pi }{3}}{\rm Y}_{1,1}\sin

\omega t, \end{aligned}$$ (54) and $$\begin{aligned} \left[ \widetilde{\mathcal {U}}_t\right] _{33}= & {} \cos ^2\theta +\sin ^2\theta \cos \omega t \nonumber \\= & {}

\frac{\sqrt{4\pi }}{3}{\rm Y}_{0,0}+\sqrt{\frac{16\pi }{45}}{\rm Y}_{2,0} +\left( \frac{\sqrt{16\pi }}{3}{\rm Y}_{0,0}-\sqrt{\frac{16\pi }{45}}{\rm Y}c_{2,0}\right) \cos \omega t.

\end{aligned}$$ (55) CHANGE HISTORY * _ 07 SEPTEMBER 2021 A Correction to this paper has been published: https://doi.org/10.1038/s41598-021-95950-3 _ REFERENCES * Breuer, H.-P. &

Petruccione, F. _The Theory of Open Quantum Systems_ (Oxford University Press, Oxford, 2007). Book  Google Scholar  * Weiss, U. _Quantum Dissipative Systems_, 4th edn. (World Scientific,

Singapore, 2012). Book  Google Scholar  * Burghardt, I., May, V., Micha, D. A. & Bittner, E. R. _Energy Transfer Dynamics in Biomaterial Systems_ (Springer, Berlin, 2009). Book  Google

Scholar  * Layfield, J. P. & Hammes-Schiffer, S. Hydrogen tunneling in enzymes and biomimetic models._ Chem. Rev._ 114, 3466–3494, https://doi.org/10.1021/cr400400p (2014). Article  CAS

  PubMed  Google Scholar  * Lambert, N. et al. Quantum biology. _Nat. Phys._ 9, 10–18, https://doi.org/10.1038/nphys2474 (2013). Article  CAS  Google Scholar  * Chen, H.-B., Lien, J.-Y.,

Hwang, C.-C. & Chen, Y.-N. Long-lived quantum coherence and non-markovianity of photosynthetic complexes. _Phys. Rev. E_ 89, 042147, https://doi.org/10.1103/PhysRevE.89.042147 (2014).

Article  ADS  CAS  Google Scholar  * Chen, H.-B., Lambert, N., Cheng, Y.-C., Chen, Y.-N. & Nori, F. Using non-markovian measures to evaluate quantum master equations for photosynthesis.

_Sci. Rep._ 5, 12753, https://doi.org/10.1038/srep12753 (2015). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Chen, H.-B., Chiu, P.-Y. & Chen, Y.-N. Vibration-induced

coherence enhancement of the performance of a biological quantum heat engine. _Phys. Rev. E_ 94, 052101, https://doi.org/10.1103/PhysRevE.94.052101 (2016). Article  ADS  PubMed  Google

Scholar  * de Vega, I. & Alonso, D. Dynamics of non-markovian open quantum systems. _Rev. Mod. Phys._ 89, 015001, https://doi.org/10.1103/RevModPhys.89.015001 (2017). Article  ADS 

MathSciNet  Google Scholar  * Ladd, T. D. et al. Quantum computers. _Nature_ 464, 45, https://doi.org/10.1038/nature08812 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Buluta, I.,

Ashhab, S. & Nori, F. Natural and artificial atoms for quantum computation. _Rep. Prog. Phys._ 74, 104401 (2011). Article  ADS  Google Scholar  * Preskill, J. Quantum Computing in the

NISQ era and beyond. _Quantum_ 2, 79 (2018). Article  Google Scholar  * Rivas, A., Huelga, S. F. & Plenio, M. B. Quantum non-markovianity: characterization, quantification and detection.

_Rep. Prog. Phys._ 77, 094001, https://doi.org/10.1088/0034-4885/77/9/094001 (2014). Article  ADS  MathSciNet  PubMed  Google Scholar  * Breuer, H.-P., Laine, E.-M., Piilo, J. &

Vacchini, B. Colloquium: Non-markovian dynamics in open quantum systems. _Rev. Mod. Phys._ 88, 021002, https://doi.org/10.1103/RevModPhys.88.021002 (2016). Article  ADS  Google Scholar  *

Chruściński, D. & Maniscalco, S. Degree of non-markovianity of quantum evolution. _Phys. Rev. Lett._ 112, 120404, https://doi.org/10.1103/PhysRevLett.112.120404 (2014). Article  ADS  CAS

  PubMed  Google Scholar  * Chen, H.-B., Lien, J.-Y., Chen, G.-Y. & Chen, Y.-N. Hierarchy of non-markovianity and \(k\)-divisibility phase diagram of quantum processes in open systems.

_Phys. Rev. A_ 92, 042105, https://doi.org/10.1103/PhysRevA.92.042105 (2015). Article  ADS  CAS  Google Scholar  * Chen, H.-B., Chen, G.-Y. & Chen, Y.-N. Thermodynamic description of

non-markovian information flux of nonequilibrium open quantum systems. _Phys. Rev. A_ 96, 062114, https://doi.org/10.1103/PhysRevA.96.062114 (2017). Article  ADS  Google Scholar  * Luo, Y.,

Li, Y., Shao, L.-H. & Xi, Z. Quantifying quantum non-markovianity via one-shot generalised mutual information. _Laser Phys. Lett._ 17, 035203, https://doi.org/10.1088/1612-202x/ab6991

(2020). Article  ADS  Google Scholar  * Kossakowski, A. A class of linear positive maps in matrix algebras. _Open Syst. Info. Dyn._ 10, 213–220, https://doi.org/10.1023/A:1025101606680

(2003). Article  MathSciNet  MATH  Google Scholar  * Benatti, F. & Floreanini, R. Open quantum dynamics: Complete positivity and entanglement. _Int. J. Mod. Phys. B_ 19, 3063–3139,

https://doi.org/10.1142/S0217979205032097 (2005). Article  ADS  MathSciNet  MATH  Google Scholar  * Dominy, J. M., Shabani, A. & Lidar, D. A. A general framework for complete positivity.

_Quant. Info. Proc._ 15, 465–494, https://doi.org/10.1007/s11128-015-1148-0 (2016). Article  MathSciNet  MATH  Google Scholar  * Chruściński, D. & Pascazio, S. A brief history of the

gkls equation. _Open Syst. Info. Dyn._ 24, 1740001, https://doi.org/10.1142/S1230161217400017 (2017). Article  MathSciNet  MATH  Google Scholar  * Kraus, K. States, _Effects, and Operations:

Fundamental Notions of Quantum Theory_ (Springer, Berlin, Heidelberg, 1983). Book  Google Scholar  * Nielsen, M. A. & Chuang, I. L. _Quantum Compution and Quantum Information_

(Cambridge University Press, Cambridge, England, 2000). Google Scholar  * Jamiołkowski, A. Linear transformations which preserve trace and positive semidefiniteness of operators. _Rep. Math.

Phys._ 3, 275–278, https://doi.org/10.1016/0034-4877(72)90011-0 (1972). Article  ADS  MathSciNet  MATH  Google Scholar  * Choi, M.-D. Completely positive linear maps on complex matrices.

_Linear Alg. Appl._ 10, 285–290. https://doi.org/10.1016/0024-3795(75)90075-0 (1975). Article  MathSciNet  MATH  Google Scholar  * Gorini, V., Kossakowski, A. & Sudarshan, E. C. G.

Completely positive dynamical semigroups of n-level systems. _J. Math. Phys._ 17, 821–825, https://doi.org/10.1063/1.522979 (1976). Article  ADS  MathSciNet  MATH  Google Scholar  *

Lindblad, G. On the generators of quantum dynamical semigroups. _Comm. Math. Phys._ 48, 119–130, https://doi.org/10.1007/BF01608499 (1976). Article  ADS  MathSciNet  MATH  Google Scholar  *

Leggett, A. J. et al. Dynamics of the dissipative two-state system. _Rev. Mod. Phys._ 59, 1–85, https://doi.org/10.1103/RevModPhys.59.1 (1987). Article  ADS  CAS  Google Scholar  * Grabert,

H., Schramm, P. & Ingold, G.-L. Quantum brownian motion: The functional integral approach. _Phys. Rep._ 168, 115–207, https://doi.org/10.1016/0370-1573(88)90023-3 (1988). Article  ADS 

MathSciNet  CAS  Google Scholar  * Grifoni, M. & Hänggi, P. Driven quantum tunneling. _Phys. Rep._ 304, 229–354, https://doi.org/10.1016/S0370-1573(98)00022-2 (1998). Article  ADS 

MathSciNet  CAS  Google Scholar  * Tanimura, Y. Nonperturbative expansion method for a quantum system coupled to a harmonic-oscillator bath. _Phys. Rev. A_ 41, 6676–6687,

https://doi.org/10.1103/PhysRevA.41.6676 (1990). Article  ADS  MathSciNet  CAS  PubMed  Google Scholar  * Tanimura, Y. & Kubo, R. Time evolution of a quantum system in contact with a

nearly gaussian-markoffian noise bath. _J. Phys. Soc. Jpn._ 58, 101–114, https://doi.org/10.1143/JPSJ.58.101 (1989). Article  ADS  MathSciNet  Google Scholar  * Tanimura, Y. Stochastic

liouville, langevin, fokker-planck, and master equation approaches to quantum dissipative systems. _J. Phys. Soc. Jpn._ 75, 082001, https://doi.org/10.1143/JPSJ.75.082001 (2006). Article 

ADS  CAS  Google Scholar  * Iles-Smith, J., Lambert, N. & Nazir, A. Environmental dynamics, correlations, and the emergence of noncanonical equilibrium states in open quantum systems.

_Phys. Rev. A_ 90, 032114, https://doi.org/10.1103/PhysRevA.90.032114 (2014). Article  ADS  CAS  Google Scholar  * Garg, A., Onuchic, J. N. & Ambegaokar, V. Effect of friction on

electron transfer in biomolecules. _J. Chem. Phys._ 83, 4491–4503, https://doi.org/10.1063/1.449017 (1985). Article  ADS  CAS  Google Scholar  * Shibata, F. & Arimitsu, T. Expansion

formulas in nonequilibrium statistical mechanics. _J. Phys. Soc. Jpn._ 49, 891–897. https://doi.org/10.1143/JPSJ.49.891 (1980). Article  ADS  Google Scholar  * Mukamel, S., Oppenheim, I.

& Ross, J. Statistical reduction for strongly driven simple quantum systems. _Phys. Rev. A_ 17, 1988–1998, https://doi.org/10.1103/PhysRevA.17.1988 (1978). Article  ADS  MathSciNet  CAS

  Google Scholar  * Palenberg, M. A., Silbey, R. J., Warns, C. & Reineker, P. Local and nonlocal approximation for a simple quantum system. _J. Chem. Phys._ 114, 4386–4389 (2001).

Article  ADS  CAS  Google Scholar  * Wigner, E. P. On the quantum correction for thermodynamic equilibrium. _Phys. Rev._ 40, 749–759, https://doi.org/10.1103/PhysRev.40.749 (1932). Article 

ADS  CAS  MATH  Google Scholar  * Glauber, R. J. Coherent and incoherent states of the radiation field. _Phys. Rev._ 131, 2766–2788, https://doi.org/10.1103/PhysRev.131.2766 (1963). Article

  ADS  MathSciNet  MATH  Google Scholar  * Sudarshan, E. C. G. Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams. _Phys. Rev. Lett._ 10, 277–279,

https://doi.org/10.1103/PhysRevLett.10.277 (1963). Article  ADS  MathSciNet  MATH  Google Scholar  * Zurek, W. H. Decoherence, einselection, and the quantum origins of the classical. _Rev.

Mod. Phys._ 75, 715–775, https://doi.org/10.1103/RevModPhys.75.715 (2003). Article  ADS  MathSciNet  MATH  Google Scholar  * Schlosshauer, M. Decoherence, the measurement problem, and

interpretations of quantum mechanics. _Rev. Mod. Phys._ 76, 1267–1305, https://doi.org/10.1103/RevModPhys.76.1267 (2005). Article  ADS  Google Scholar  * Modi, K., Brodutch, A., Cable, H.,

Paterek, T. & Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. _Rev. Mod. Phys._ 84, 1655–1707, https://doi.org/10.1103/RevModPhys.84.1655

(2012). Article  ADS  Google Scholar  * Schlosshauer, M. _Decoherence and the Quantum-to-Classical Transition_ (Springer, Berlin, 2007). Google Scholar  * Chen, H.-B., Gneiting, C., Lo,

P.-Y., Chen, Y.-N. & Nori, F. Simulating open quantum systems with hamiltonian ensembles and the nonclassicality of the dynamics. _Phys. Rev. Lett._ 120, 030403,

https://doi.org/10.1103/PhysRevLett.120.030403 (2018). Article  ADS  CAS  PubMed  Google Scholar  * Chen, H.-B. et al. Quantifying the nonclassicality of pure dephasing. _Nat. Commun._ 10,

3794, https://doi.org/10.1038/s41467-019-11502-4 (2019). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Gneiting, C., Anger, F. R. & Buchleitner, A. Incoherent ensemble

dynamics in disordered systems. _Phys. Rev. A_ 93, 032139, https://doi.org/10.1103/PhysRevA.93.032139 (2016). Article  ADS  Google Scholar  * Kropf, C. M., Gneiting, C. & Buchleitner, A.

Effective dynamics of disordered quantum systems. _Phys. Rev. X_ 6, 031023, https://doi.org/10.1103/PhysRevX.6.031023 (2016). Article  CAS  Google Scholar  * Kropf, C. M., Shatokhin, V. N.

& Buchleitner, A. Open system model for quantum dynamical maps with classical noise and corresponding master equations. _Open Syst. Inf. Dyn._ 24, 1740012.

https://doi.org/10.1142/S1230161217400121 (2017). Article  MathSciNet  MATH  Google Scholar  * Gneiting, C. & Nori, F. Disorder-induced dephasing in backscattering-free quantum

transport. _Phys. Rev. Lett._ 119, 176802, https://doi.org/10.1103/PhysRevLett.119.176802 (2017). Article  ADS  PubMed  Google Scholar  * Myatt, C. J. et al. Decoherence of quantum

superpositions through coupling to engineered reservoirs. _Nature_ 403, 269–273, https://doi.org/10.1038/35002001 (2000). Article  ADS  CAS  PubMed  Google Scholar  * Liu, B.-H. et al.

Experimental control of the transition from markovian to non-markovian dynamics of open quantum systems. _Nat. Phys._ 7, 931–934, https://doi.org/10.1038/nphys2085 (2011). Article  CAS 

Google Scholar  * Liu, Z.-D. et al. Experimental implementation of fully controlled dephasing dynamics and synthetic spectral densities. _Nat. Commun._ 9, 3453,

https://doi.org/10.1038/s41467-018-05817-x (2018). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Lo Franco, R., Bellomo, B., Andersson, E. & Compagno, G. Revival of

quantum correlations without system–environment back-action. _Phys. Rev. A_ 85, 032318, https://doi.org/10.1103/PhysRevA.85.032318 (2012). Article  ADS  CAS  Google Scholar  * Xu, J.-S. et

al. Experimental recovery of quantum correlations in absence of system–environment back-action. _Nat. Commun._ 4, 2851, https://doi.org/10.1038/ncomms3851 (2013). Article  ADS  CAS  PubMed 

Google Scholar  * Ollivier, H. & Zurek, W. H. Quantum discord: A measure of the quantumness of correlations. _Phys. Rev. Lett._ 88, 017901, https://doi.org/10.1103/PhysRevLett.88.017901

(2001). Article  ADS  CAS  PubMed  MATH  Google Scholar  * Dakić, B., Vedral, V. & Brukner, C. Necessary and sufficient condition for nonzero quantum discord._ Phys. Rev. Lett._ 105,

190502, https://doi.org/10.1103/PhysRevLett.105.190502 (2010). Article  ADS  CAS  PubMed  MATH  Google Scholar  * Bochner, S. Monotone funktionen, stieltjessche integrale und harmonische

analyse. _Math. Ann._ 108, 378–410, https://doi.org/10.1007/BF01452844 (1933). Article  MathSciNet  MATH  Google Scholar  * Addis, C., Brebner, G., Haikka, P. & Maniscalco, S. Coherence

trapping and information backflow in dephasing qubits. _Phys. Rev. A_ 89, 024101, https://doi.org/10.1103/PhysRevA.89.024101 (2014). Article  ADS  CAS  Google Scholar  * Roszak, K. &

Cywiński, L. Characterization and measurement of qubit-environment-entanglement generation during pure dephasing. _Phys. Rev. A_ 92, 032310, https://doi.org/10.1103/PhysRevA.92.032310

(2015). Article  ADS  CAS  Google Scholar  * Roszak, K. & Cywiński, L. Equivalence of qubit-environment entanglement and discord generation via pure dephasing interactions and the

resulting consequences. _Phys. Rev. A_ 97, 012306, https://doi.org/10.1103/PhysRevA.97.012306 (2018). Article  ADS  CAS  Google Scholar  * Roszak, K. Criteria for system–environment

entanglement generation for systems of any size in pure-dephasing evolutions. _Phys. Rev. A_ 98, 052344, https://doi.org/10.1103/PhysRevA.98.052344 (2018). Article  ADS  Google Scholar  *

Roszak, K., Kwiatkowski, D. & Cywiński, L. How to detect qubit-environment entanglement generated during qubit dephasing. _Phys. Rev. A_ 100, 022318,

https://doi.org/10.1103/PhysRevA.100.022318 (2019). Article  ADS  CAS  Google Scholar  * Audenaert, K. M. R. & Scheel, S. On random unitary channels. _New J. Phys._ 10, 023011 (2008).

Article  ADS  Google Scholar  * Childress, L. et al. Coherent dynamics of coupled electron and nuclear spin qubits in diamond. _Science_ 314, 281–285, https://doi.org/10.1126/science.1131871

(2006). Article  ADS  CAS  PubMed  Google Scholar  * Fuchs, G. D., Dobrovitski, V. V., Toyli, D. M., Heremans, F. J. & Awschalom, D. D. Gigahertz dynamics of a strongly driven single

quantum spin. _Science_ 326, 1520–1522, https://doi.org/10.1126/science.1181193 (2009). Article  ADS  CAS  PubMed  Google Scholar  * Maurer, P. C. et al. Room-temperature quantum bit memory

exceeding one second. _Science_ 336, 1283–1286, https://doi.org/10.1126/science.1220513 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Redman, D. A., Brown, S., Sands, R. H. &

Rand, S. C. Spin dynamics and electronic states of n-v centers in diamond by epr and four-wave-mixing spectroscopy. _Phys. Rev. Lett._ 67, 3420–3423,

https://doi.org/10.1103/PhysRevLett.67.3420 (1991). Article  ADS  CAS  PubMed  Google Scholar  * Neumann, P. et al. Multipartite entanglement among single spins in diamond. _Science_ 320,

1326–1329, https://doi.org/10.1126/science.1157233 (2008). Article  ADS  CAS  PubMed  Google Scholar  * Liu, G.-Q., Pan, X.-Y., Jiang, Z.-F., Zhao, N. & Liu, R.-B. Controllable effects

of quantum fluctuations on spin free-induction decay at room temperature. _Sci. Rep._ 2, 432, https://doi.org/10.1038/srep00432 (2012). Article  CAS  PubMed  PubMed Central  Google Scholar 

* Maze, J. R. et al. Free induction decay of single spins in diamond. _New J. Phys._ 14, 103041, https://doi.org/10.1088/1367-2630/14/10/103041 (2012). Article  ADS  CAS  Google Scholar  *

Balasubramanian, G. et al. Ultralong spin coherence time in isotopically engineered diamond. _Nat. Mater._ 8, 383, https://doi.org/10.1038/nmat2420 (2009). Article  ADS  MathSciNet  CAS 

PubMed  Google Scholar  * Jacques, V. et al. Dynamic polarization of single nuclear spins by optical pumping of nitrogen-vacancy color centers in diamond at room temperature. _Phys. Rev.

Lett._ 102, 057403, https://doi.org/10.1103/PhysRevLett.102.057403 (2009). Article  ADS  CAS  PubMed  Google Scholar  * London, P. et al. Detecting and polarizing nuclear spins with double

resonance on a single electron spin. _Phys. Rev. Lett._ 111, 067601, https://doi.org/10.1103/PhysRevLett.111.067601 (2013). Article  ADS  CAS  PubMed  Google Scholar  * Rahimi-Keshari, S. et

al. Quantum process nonclassicality. _Phys. Rev. Lett._ 110, 160401, https://doi.org/10.1103/PhysRevLett.110.160401 (2013). Article  ADS  CAS  PubMed  Google Scholar  * Sabapathy, K. K.

Process output nonclassicality and nonclassicality depth of quantum-optical channels. _Phys. Rev. A_ 93, 042103, https://doi.org/10.1103/PhysRevA.93.042103 (2016). Article  ADS  CAS  Google

Scholar  * Hsieh, J.-H., Chen, S.-H. & Li, C.-M. Quantifying quantum-mechanical processes. _Sci. Rep._ 7, 13588, https://doi.org/10.1038/s41598-017-13604-9 (2017). Article  CAS  PubMed 

Google Scholar  * Smirne, A., Egloff, D., Díaz, M. G., Plenio, M. B. & Huelga, S. F. Coherence and non-classicality of quantum markov processes. _Quantum Sci. Technol._ 4, 01LT01.

https://doi.org/10.1088/2058-9565/aaebd5 (2019). * Pernice, A., Helm, J. & Strunz, W. T. System–environment correlations and non-markovian dynamics. _J. Phys. B: At. Mol. Opt. Phys._ 45,

154005, https://doi.org/10.1088/0953-4075/45/15/154005 (2012). Article  ADS  CAS  Google Scholar  * Chruściński, D. & Wudarski, F. A. Non-markovianity degree for random unitary

evolution. _Phys. Rev. A_ 91, 012104, https://doi.org/10.1103/PhysRevA.91.012104 (2015). Article  ADS  MathSciNet  CAS  Google Scholar  * Wudarski, F. A. & Chruściński, D. Markovian

semigroup from non-markovian evolutions. _Phys. Rev. A_ 93, 042120. https://doi.org/10.1103/PhysRevA.93.042120 (2016). Article  ADS  CAS  Google Scholar  * Breuer, H.-P., Amato, G. &

Vacchini, B. Mixing-induced quantum non-markovianity and information flow. _New J. Phys._ 20, 043007, https://doi.org/10.1088/1367-2630/aab2f9 (2018). Article  ADS  Google Scholar  * Milz,

S. et al. When is a non-markovian quantum process classical? _Phys. Rev. X_ 10, 041049, https://doi.org/10.1103/PhysRevX.10.041049 (2020). Article  CAS  Google Scholar  * Benedetti, C.,

Salari Sehdaran, F., Zandi, M. H. & Paris, M. G. A. Quantum probes for the cutoff frequency of ohmic environments. _Phys. Rev. A_ 97, 012126, https://doi.org/10.1103/PhysRevA.97.012126

(2018). Article  ADS  CAS  Google Scholar  * Gebbia, F. et al. Two-qubit quantum probes for the temperature of an ohmic environment. _Phys. Rev. A_ 101, 032112.

https://doi.org/10.1103/PhysRevA.101.032112 (2020). Article  ADS  MathSciNet  CAS  Google Scholar  * Candeloro, A. & Paris, M. G. A. Discrimination of ohmic thermal baths by quantum

dephasing probes. _Phys. Rev. A_ 103, 012217, https://doi.org/10.1103/PhysRevA.103.012217 (2021). Article  ADS  MathSciNet  CAS  Google Scholar  * Mirkin, N., Larocca, M. & Wisniacki, D.

Quantum metrology in a non-markovian quantum evolution. _Phys. Rev. A_ 102, 022618, https://doi.org/10.1103/PhysRevA.102.022618 (2020). Article  ADS  MathSciNet  CAS  Google Scholar  *

Vázquez, P. C. L. & Gorin, T. Probing the dynamics of an open quantum system via a single qubit. _J. Phys. A: Math. Theor._ 53, 355301, https://doi.org/10.1088/1751-8121/ab9edc (2020).

Article  MathSciNet  Google Scholar  * Hensen, B. _et al._ Loophole-free bell inequality violation using electron spins separated by 1.3 kilometres. _Nature_ 526, 682,

https://doi.org/10.1038/nature15759 (2015). * Schmitt, S. et al. Submillihertz magnetic spectroscopy performed with a nanoscale quantum sensor. _Science_ 356, 832–837,

https://doi.org/10.1126/science.aam5532 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Du, C. et al. Control and local measurement of the spin chemical potential in a magnetic

insulator. _Science_ 357, 195–198, https://doi.org/10.1126/science.aak9611 (2017). Article  ADS  CAS  PubMed  Google Scholar  Download references ACKNOWLEDGEMENTS This work is supported by

Ministry of Science and Technology, Taiwan, Grants No. MOST 108-2112-M-006-020-MY2, MOST 109-2112-M-006-012, MOST 107-2628-M-006-002-MY3, and MOST 109-2627-M-006-004, and Army Research

Office, Grant No. W911NF-19-1-0081. H.-B.C. would also like to acknowledge the support by Higher Education Sprout Project, Ministry of Education to the Headquarters of University Advancement

at NCKU. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Engineering Science, National Cheng Kung University, Tainan, 70101, Taiwan Hong-Bin Chen * Center for Quantum Frontiers

of Research and Technology, NCKU, Tainan, 70101, Taiwan Hong-Bin Chen & Yueh-Nan Chen * Department of Physics, National Cheng Kung University, Tainan, 70101, Taiwan Yueh-Nan Chen Authors

* Hong-Bin Chen View author publications You can also search for this author inPubMed Google Scholar * Yueh-Nan Chen View author publications You can also search for this author inPubMed 

Google Scholar CONTRIBUTIONS Both authors are responsible for all the content of this work. CORRESPONDING AUTHORS Correspondence to Hong-Bin Chen or Yueh-Nan Chen. ETHICS DECLARATIONS

COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published

maps and institutional affiliations. The original online version of this Article was revised: In the original version of this Article, Yueh-Nan Chen was omitted as a corresponding author.

Correspondence and request for materials should be addressed to Hong Bin Chen and Yueh-Nan Chen. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons

Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original

author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the

article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your

intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence,

visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Chen, HB., Chen, YN. Canonical Hamiltonian ensemble representation of

dephasing dynamics and the impact of thermal fluctuations on quantum-to-classical transition. _Sci Rep_ 11, 10046 (2021). https://doi.org/10.1038/s41598-021-89400-3 Download citation *

Received: 24 September 2020 * Accepted: 26 April 2021 * Published: 11 May 2021 * DOI: https://doi.org/10.1038/s41598-021-89400-3 SHARE THIS ARTICLE Anyone you share the following link with

will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt

content-sharing initiative