Magnetoconductivity in quasiperiodic graphene superlattices

ABSTRACT The magnetoconductivity in Fibonacci graphene superlattices is investigated in a perpendicular magnetic field _B_. It was shown that the _B_-dependence of the diffusive conductivity

exhibits a complicated oscillatory behavior whose characteristics cannot be associated with Weiss oscillations, but rather with Shubnikov-de Haas ones. The absense of Weiss oscillations is

attributed to the existence of two incommensurate periods in Fibonacci superlattices. It was also found that the quasiperiodicity of the structure leads to a renormalization of the Fermi

velocity \(v_{F}\) of graphene. Our calculations revealed that, for weak _B_, the dc Hall conductivity \(\sigma _{yx}\) exhibits well defined and robust plateaux, where it takes the

unexpected values \(\pm 4e^{2}/\hslash \left( 2N+1\right) \), indicating that the half-integer quantum Hall effect does not occur in the considered structure. It was finally shown that

\(\sigma _{yx}\) displays self-similarity for magnetic fields related by \(\tau ^{2}\) and \(\tau ^{4}\), where \(\tau \) is the golden mean. SIMILAR CONTENT BEING VIEWED BY OTHERS

UNCONVENTIONAL SUPERCONDUCTIVITY IN MAGIC-ANGLE TWISTED TRILAYER GRAPHENE Article Open access 13 January 2022 LONG-RANGE BALLISTIC TRANSPORT OF BROWN-ZAK FERMIONS IN GRAPHENE SUPERLATTICES

Article Open access 13 November 2020 PROBING MINIBAND STRUCTURE AND HOFSTADTER BUTTERFLY IN GATED GRAPHENE SUPERLATTICES VIA MAGNETOTRANSPORT Article Open access 09 September 2023

INTRODUCTION After the experimental realization of graphene1, a great deal of attention has been paid to the study of its magnetotransport properties. The early studies2,3,4,5 revealed that,

when monolayer graphene is subject to a perpendicular magnetic field \(\overrightarrow{B}\), the magnetoconductivity \(\sigma _{\alpha \beta }\) exhibit unusual properties, such as the

anomalous integer quantum Hall effect. The latter is directly associated with the presence of the \(n=0\) Landau level (LL) in the nonequidistant and highly degenerate energy spectrum,

\(E_{n}=sgn(n)\hslash \omega _{C}\sqrt{\left| n\right| }\), of single layer graphene6, where \(\hslash \omega _{C}=\sqrt{2}\hslash v_{F}/l_{B}\) is the cyclotron energy,

\(l_{B}=\sqrt{\hslash c/eB}\) the magnetic length, \(v_{F}\) the Fermi velocity and \(n=0,\pm 1,\pm 2,\ldots \) the energy quantum number. In subsequent studies, the effects of a

one-dimensional (1D) periodic potential \(V_{P}(x)\) on the LLs and on the corresponding magnetoconductivity characteristics were investigated. In this case, the degeneracy of each LL is in

general lifted, which leads to the formation of magnetic subbands. Further, it should be remarked that the effects of \(V_{P}(x)\) on the magnetoconductivity are usually described in terms

of the chemical potential \(\mu \) (or charge-carrier concentration) or the magnetic field intensity _B_, for fixed values of the remaining physical parameters. In the former description, it

was demonstrated that the dc-magnetoconductivity response, which will be the focus of our attention, depends on the range of superlattice-potential and magnetic-field strengths

considered7,8,9. In particular, it was found that the diagonal conductivity displays a strong anisotropy reversal when the magnetic field go from weak to intermediate strength, whereas the

Hall conductivity exhibit plateaux for weak fields, which tend to disappear for intermediate ones. In the second description, most of the work focusses on the oscillations with _B_ of the

magnetoconductivity, especially on the Shubnikov-de Haas (SdH) and Weiss or commensurability oscillations10,11,12,13,14. It was shown theoretically that the Weiss oscillations in monolayer

graphene are enhanced relative to those of ordinary 2D electron gas, and are more robust against temperature damping in the small magnetic field regime10. The experimental observation of

commensurability oscillations in 1D-graphene superlattices (GSLs) was reported for the first time very recently14. The study of magnetoconductivity oscillations has been also carried out for

other periodically modulated two-dimensional (2D) systems, such as bilayer graphene15 and phosphorene16. Furthermore, if the periodic potential \(V_{P}(x)\) in monolayer graphene is

replaced by an aperiodic one _V_(_x_), such as Fibonacci, Thue-Morse and period-doubling potentials, it is expected that, due to the presence of exotic electronic spectra in the resulting 2D

system, the corresponding magnetotransport properties may exhibit unusual characteristics. It is the purpose of this work to explore some of these characteristics, which, up to now, have

not received a special attention. To carry out the study, we will use the Fibonacci GSL. This is because it represents, from a theoretical and experimental point of view, a simple and

accessible quasiperiodic structure exhibiting fractal and self-similar properties not shared by other aperiodic systems. In particular, it was shown theoretically that the electronic spectra

of GSLs exhibit a multifractal structure, which manifests in the properties of different transport quantities in the absence17 and presence18 of external fields. A further motivation to use

Fibonacci GSLs is associated with the possibility of studying experimentally their magnetoconductivity characteristics, as occur for GaAs/AlGaAs Fibonacci lateral SLs19, where complicated

commensurability oscillations of the magnetoresistence were observed. The paper is organized as follows. In Sect. 2, we present the theoretical approach. Section 3 is devoted to the results

and the corresponding discussions. Finally, the conclusions are presented in Sect. 4. THEORY As mentioned above, in this work we are concerned with the dc conductivity in quasiperiodic

Fibonacci GSLs in a perpendicular magnetic field \(\overrightarrow{B}=B{\widehat{z}}\). Specifically, we will focus our attention on the diffusive (band) \(\sigma _{yy}\) and Hall \(\sigma

_{yx}\) conductivities, ignoring the collisional one, which is determined by transport through localized states. We use the Landau gauge \(\overrightarrow{A}=(0,Bx,0)\) for the vector

potential and take the Fibonacci SL potential _V_(_x_) along the _x_-axis. To perform the calculations we will use the Kubo formula for \(\sigma _{yy}\) and \(\sigma _{yx}\), which, for

non-interacting electrons in the LL representation, can be written down as20,21 $$\begin{aligned} \sigma _{yy}= & {} \frac{\beta \tau }{S}\sum \limits

_{i}f(E_{i})[1-f(E_{i})]\left\langle i\left| J_{y}\right| i\right\rangle ^{2}, \end{aligned}$$ (1) $$\begin{aligned} \sigma _{yx}= & {} -\frac{i\hslash }{S}\sum \limits _{i\text { }\ne

\text { j}}\frac{ \left[ f\left( E_{i}\right) -f\left( E_{j}\right) \right] }{\left( E_{i}-E_{j}\right) ^{2}+\Gamma ^{2}}\left\langle i\left| J_{y}\right| j\right\rangle \left\langle j\left|

J_{x}\right| i\right\rangle , \end{aligned}$$ (2) where \(S=L_{x}L_{y}\) is the SL area, \(\beta =1/k_{B}T\), _f_(_E_) the Fermi distribution function, \(J_{\alpha }=-ev_{F}\sigma _{\alpha

}\) the \(\alpha \)-component of the current operator \(\overrightarrow{J}\), \(\sigma _{\alpha }\) the Pauli matrix, \(\Gamma \) the LL broadening parameter, and \(\tau \) the scattering

time, which we assumed constant for all states. For low energy excitations around the _K_ point of the Brillouin zone, \(E_{\nu }\) and \(\left| \nu \right) \), with \(\nu =i,j\) in Eqs. (1)

and (2), are the eigenvalues and eigenfunctions of the massless Dirac-like equation. We can then write \(\left| \nu \right) \) in coordinate representation in the form22: $$\begin{aligned}

\left| \nu \right) ={\ }\left| n,k_{y}\right) = \frac{\exp (-iyk_{y})}{\sqrt{L_{y}}}\Phi _{nk_{y}}(x)\,, \end{aligned}$$ (3) where \(n=0,\pm 1,\pm 2,\ldots \) is the energy quantum number,

\(k_{y}\) is the conserved wavevector along the _y_-axis, and the spinor \(\Phi _{nk_{y}}(x)\) satisfies the system of differential equations22: $$\begin{aligned} {\widehat{h}}\Phi

_{nk_{y}}(x)= & {} \left[ {\widehat{H}}_{0}+V(x)I\right] \Phi _{nk_{y}}(x)=E_{n}(k_{y}) \Phi _{nk_{y}}(x)\,, \end{aligned}$$ (4) $$\begin{aligned} {\widehat{H}}_{0}= & {} \left(

\begin{array}{cc} 0 &{} \hslash \omega _{c}{\widehat{a}}^{-} \\ \hslash \omega _{c}{\widehat{a}}^{\dagger } &{} 0 \end{array} \right) \,, \end{aligned}$$ (5) _I_ being the \(2\times

2\) unit matrix, \({\widehat{a}}^{\pm }=(l_{B}/\sqrt{2})\left[ {\widehat{k}}_{x}\pm i(x-x_{0})/l_{B}^{2}\right] \) the raising and lowering operators, \({\widehat{k}}_{x}=-i\partial

/\partial x\) and \(x_{0}=k_{y}l_{B}^{2}\) the conserved center position. It is clear that to calculate \(\sigma _{yy}\) and \(\sigma _{yx}\), for given values of \(\Gamma \) and the

chemical potential \(\mu \), it is necessary to solve first the eigenvalue problem for the energy operator \({\widehat{h}}\), which is only possible if the Fibonacci SL potential _V_(_x_) is

known. Here we suppose that _V_(_x_) is formed by rectangular barriers (layers _a_) and wells (layers _b_) arranged according to the Fibonacci sequence23: $$\begin{aligned} W_{n}=\left\{

\begin{array}{l} W_{n-2}\,|\,W_{n-1}\,,\,\,\,\, \text {for}\,\,\,\,n\ge 3\,\,\text {and}\,\,\,\,\text {odd} \\ W_{n-1}\,|\,W_{n-2}\,,\,\,\,\, \text {for}\,\,\,\,n\ge 3\,\,\text

{and}\,\,\,\,\text {even} \end{array} \right. , \end{aligned}$$ (6) where \(W_{1}=a\) and \(W_{2}=b\). We assume that \(V(x)=V_{0}/2\) in the barriers and \(-V_{0}/2\) in the wells. Now,

when using the potential _V_(_x_) associated with \(W_{n} \) to solving Eq. (4), the origin of coordinates is taken at the inversion center of \({\overline{W}}_{n}\), which is obtained from

\(W_{n}\) by removing its two extreme layers24. It should be pointed out that the transformations \((ab\rightarrow a,abb\rightarrow b)\) and \((b\rightarrow a,ab\rightarrow b)\) transfer the

element \(W_{n}\) into \(W_{n-2}\) and the reverse of \(W_{n-1}\), respectively, indicating that the Fibonacci SLs exibit a fractal or self-similar structure. Consequently, to obtain

self-similarity in the length scale23, it is necessary that \(d_{b}/d_{a}=\tau =(1+\sqrt{5})/2\), where \(\tau \) is the golden mean, \(d_{a}\) the barrier width and \(d_{b}\) the well

width. A simple inspection of Eq. (6) indicates that the spatial separation between adjacent interfaces is \(d_a\) or \(d_b=\tau \,d_a\), with \(d_a\) and \(d_b\) arranged according to a

Fibonacci sequence. This means that \(d_a\) (\(d_b\)) corresponds to a periodic spacing between interfaces with period \(d_a\) (\(d_b\)). Since \(d_a\) and \(d_b\) are relatively irrational,

a Fibonacci SL represents a quasiperiodic structure with two incommensurate periods. RESULTS AND DISCUSSION At this point, it should be noted that, according to the above discussion, a

quasiperiodic Fibonacci SL is an infinite self-similar structure generated according to \(W_n\) for \(n\rightarrow \infty \). In contrast to infinite periodic SLs, \(W_\infty \) has not

translational symmetry and an exact and systematic procedure to study its electronic properties does not exist. It is clear however that a good description of these properties can be

achieved if \(W_\infty \) is approximated by \(W_n\) provided the order _n_ is large enough. The latter requires that the spatial length \(L(W_n)=d_a\,F_{n-2}+d_b\, F_{n-1}\) of \(W_n\) must

be sufficiently large in comparison with the corresponding magnetic length \(l_B\), where the sequence \(F_n=F_{n-2}+F_{n-1}\), with \(F_1=F_2=1\), determines the Fibonacci numbers. It is

easy to show, for instance, that the patterns \(W_{15}\), \(W_{17}\), and \(W_{19}\), with the geometrical and physical parameters defined below, satisfies these conditions. Thus, any one of

them can be used in the study of the corresponding electronic properties. Numerical calculations are performed for the \(W_{17}\) Fibonacci superlattice with \(d_{b}/d_{a}=\tau \) and weak

magnetic fields satisfying the inequality \(l_{B}>>d\), where \(d=d_{a}+\tau d_{b}\) is the average periodicity of the Fibonacci potential _V_(_x_). This allows us to use the

quasi-classical approach to understand some of the results that will be presented below. We take \(d=20\, \hbox {nm}\) and \(V_{0}/E_{F}=2\pi \), where \(E_{F}=\hslash v_{F}/d=33\, \hbox

{meV}\) is an energy scale parameter7. With that value of _d_, it is easy to show that \(d_{a}=d/(1+\tau ^{2})\approx 5.5\, \hbox {nm}\) and \(d_{b}=d_{a}\tau \approx 9\, \hbox {nm}\).

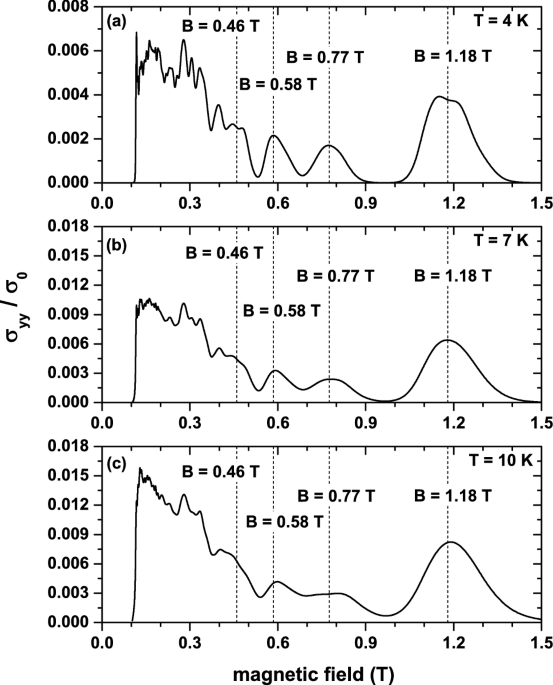
DIFFUSIVE CONDUCTIVITY Using the numerical solutions of Eqs. (4) and (3), we calculated the magnetic field dependence of the diffusive conductivity \(\sigma _{yy}\) for different

temperatures and chemical potentials \(\mu \). Such a dependence is shown in Fig. 1 for weak magnetic fields, low temperatures and \(\mu =0\). As can be seen, \(\sigma _{yy}\) displays

oscillations as a function of _B_ whose characteristics depend on the range of magnetic fields considered. For the low-field range \((0.12\lesssim B\lesssim 0.36)\), \(\sigma _{yy}\)

exhibits a complicated oscillatory behavior, characterized by relatively rapid oscillations, whereas for the higher one (\(0.36\lesssim B\lesssim 1.4\)), these oscillations are much simpler

and well-behaved. Before presenting the analysis of these results, it is interesting to note that, as mentioned in the Introduction, similar complicated oscillations of the magnetoresistence

were experimentally observed in GaAs/AlGaAs Fibonacci lateral SLs19. It was shown in that work, using a Fourier analysis, that these oscillations can be described by the superposition of a

small number of incommensurate periodic (sinusoidal) modulations, with periods successively scaled by the golden mean \(\tau \). The latter is a direct consequence of the self-similarity

properties exhibited by Fibonacci SLs. Although this approach gives useful information about such oscillations, it does not relate them to the corresponding magnetic subbands, which can give

further insight into the physical origin of these oscillations. Here we adopt the LL-energy approach to describe and understand the results depicted in Fig. 1. To carry out the study, it is

necessary to take into account that25 the Fibonacci SL broadens the Landau levels of graphene into magnetic subbands and shifts all them rigidly downwards. The _B_-dependence of this

shifting is given approximately by \(\beta (B)=-v_{0}/\tau ^{3}\), with \(v_{0}=V_{0}/\hslash \omega _{C}\approx 1/\sqrt{B}\) being the height of the barriers in units of the cyclotron

energy. These properties are illustrated in Fig. 2 for \(B=1.18\) T, 0.77 T, 0.58 T, and 0, 46 T, that are magnetic fields at which \(\sigma _{yy}\) takes maximum values. Another important

aspect is that, according to Eq. (1), if a magnetic subband is completely full or empty, its contribution to the diffusive conductivity vanishes exactly. This implies that, for sufficiently

low temperature, the minimum values of \(\sigma _{yy}\) occur at those magnetic fields for which the chemical potential \((\mu =0)\) is in between two magnetic subbands, whereas the maxima

appear (approximately) when the center of the subbands crosses the chemical potential \((\mu =0)\), as shown in Fig. 2. The distribution of maxima and minima in the high-field range

\((0.36\lesssim B\lesssim 1.4)\) are well defined because the corresponding magnetic subbands are energetically well separated (see Fig. 2). In contrast, the complicated oscillatory behavior

observed in the low-field range is due to the overlap between the subbands. For a further characterization of the \(\sigma _{yy}\) oscillations, the bandwidths of the \(n\le 5\) magnetic

subbands are depicted in Fig. 3. This choice is due to the fact that these are the subbands determining the oscillatory structure of \(\sigma _{yy}\) in Fig. 1. Now, it is seen that the

widths of the \(n=0,1,2\) subbands increase with _B_ and do not exhibit a clear oscillatory behavior, whereas those of the remaining ones increase non-monotonically with _B_ exhibiting a

slowly oscillating behavior. These bandwidth characteristics are in stark contrast to those of 1D periodic SLs, where the _B_-dependent width of the _n_-subband is proportional to the sum of

two successive Laguerre polynomials10,11,26 and, therefore, exhibits oscillations with vanishing amplitude (minima) at certain values of the field. The number of such oscillations increases

with _n_, especially in the range of weak magnetic fields, giving rise to the Weiss oscillations in the magnetoresistance, which originate from the commensurability between the SL period

and the cyclotron diameter in the 1D periodic SL. This suggests that the oscillatory structure of \(\sigma _{yy}\) shown in Fig. 1 cannot be associated with Weiss oscillations, but rather

with Shubnikov-de Haas ones. This result is a direct consequence of the existence of two in-commensurate periods in Fibonacci SLs27. Furthermore, since \(l_{B}>>d\) we can carry out a

quasiclassical analysis of the results presented in Fig. 1. In this approach, the band structure of the \(W_{17}\) Fibonacci GSL in the absence of _B_, which can be calculated considering a

periodic SL whose unit cell is based on the \(W_{17}\) potential28, is not altered by the magnetic field, which only quantizes it and the charge-carrier motion is along equal energy curves

in _k_-space. Under these conditions, we can assume that the cyclotron orbits in monolayer graphene are not substantially modified by the Fibonacci potential. Taking then into account that

the band structure of graphene is given by \(E(\overrightarrow{k})=\pm \hslash v_{F}k=\pm \hslash v_{F}\sqrt{ k_{x}^{2}+k_{y}^{2}}\), the area enclosed by the cyclotron orbit (circumference

in \(\overrightarrow{r}\)-space) associated with the Landau level \(E_{n}=sgn(n)\hslash \omega _{C}\sqrt{\left| n\right| }\) is given by $$\begin{aligned} A_{n}=\pi R_{n}^{2}=\pi

l_{B}^{4}\left( \frac{E_{n}}{\hslash v_{F}}\right) ^{2}=2\pi l_{B}^{2}\left| n\right| , \end{aligned}$$ (7) where \(R_{n}\) is the cyclotron radius. As assumed above, Eq. (7) also applies to

the case where the Fibonacci potential is considered, but replacing \(E_{n}\) and the Fermi velocity \(v_{F}\) by \(E_{n}^{\prime }\) and \(v_{F}^{\prime }\), respectively,

$$\begin{aligned} A_{n}^{\prime }=\pi R_{n}^{\prime 2}=\pi l_{B}^{4}\left( \frac{E_{n}^{\prime }}{\hslash v_{F}^{\prime }}\right) ^{2}=2\pi l_{B}^{2}\left( \frac{ E_{n}^{\prime }}{\hslash

\omega _{C}}\right) ^{2}\left( \frac{v_{F}}{ v_{F}^{\prime }}\right) ^{2}, \end{aligned}$$ (8) where \(E_{n}^{\prime }/\hslash \omega _{C}\) represents the center of the shifted _n_ magnetic

subband corresponding to the LL \(E_{n}/\hslash \omega _{C}=sgn(n)\sqrt{\left| n\right| }\) of monolayer graphene, with \(n=0,\pm 1,\pm 2,\ldots \) being the Landau index. The velocity

\(v_{F}^{\prime } \) was introduced to include a possible small modification of the cyclotron orbits. To compare the results obtained from Eqs. (7) and (8), it is necessary to take into

account that \(E_{n}/\hslash \omega _{C}\) is measured from the \(n=0\) level. This implies that \(E_{n}^{\prime }/\hslash \omega _{C}\) in Eq. (8) must be measured from the center of the

shifted \(n=0\) magnetic subband (see Fig. 2), i. e., \(\varepsilon _{n}=E_{n}^{\prime }/\hslash \omega _{C}-\beta (B)\). Consequently, when the center of the _n_ subbands crosses the \(\mu

=0\) chemical potential \(\varepsilon _{n}=0\) and thefore \(E_{n}^{\prime }/\hslash \omega _{C}=\beta (B)\). Considering now those magnetic fields _B_ for which \(\sigma _{yy}\) exhibits

maxima and requiring that \(A_{n}^{\prime }\approx A_{n}\), one obtains $$\begin{aligned} \frac{v_{F}^{\prime }}{v_{F}}\approx \sqrt{\frac{\beta (B)^{2}}{\left| n\right| }}\,.

\end{aligned}$$ (9) The numerical evaluation of this ratio is straightforward if the shifting \(\beta (B)=E_{n}^{\prime }/\hslash \omega _{C}=-(1.17,1.43,1.67,1.85)\) of the magnetic

subbands, shown in Fig. 2, and the corresponding values \(\left| n\right| =(2,3,4,5)\) of the Landau index are used in Eq. (9). This leads to the conclusion that such a ratio is independent

of _n_ and takes the value \(v_{F}^{\prime }/v_{F}\approx 0.83\approx \tau /2\), indicating that one of the effects of the Fibonacci potential is to renormalize the Fermi velocity \(v_{F}\).

Finally, one observes in Fig. 1 that when the temperature _T_ increases, the peak structure of \(\sigma _{yy}\) tends to broaden and to be suppressed, except the peak associated with the

higher magnetic field (\(B=1.18\) T), which is robust against temperature in the _T_-range considered. The latter behavior is due to the fact that the magnetic subband giving rise to that

peak (\(n = +2\) subband in Fig. 2a) is well separated from the nearest-neighbor ones, and the thermal excitations only slightly affect the corresponding peak structure, in contrast to the

remaining peaks. HALL CONDUCTIVITY Let us now pay close attention to the dc Hall conductivity \(\sigma _{yx}\), especially to its properties when the Fibonacci GSLs is subject to magnetic

fields related by integer powers of the golden mean \(\tau \). The latter choice guarantees similarity in the magnetic-field length scale of the structure23. That quantity computed from Eq.

(2) is shown in Fig. 4 as a function of the chemical potential \(\mu \) for \(B=0.18\) T, \(B^{\prime }=B\tau ^{2}=0.46\) T, \(B^{\prime \prime }=B\tau ^{4}=1.2\) T, \(V_{0}/E_{F}=2\pi \)

and sufficiently low temperatures. We see that, for all these fields, \(\sigma _{yx}\) exhibits well defined plateaux directly associated with the energy separation between the \(n=0\),

\(\pm 1,\pm 2\) magnetic subbands. Notice that the center of steps when \(\mu \) goes from holelike to electronlike carriers is situated at \(\beta (B)=-1.14\), \(-1.85\) and \(-3.1\) in

panels (a), (b) and (c), respectively, as required by the center positions of the corresponding \(n=0\) magnetic sudbands. It is interesting to note that \(\sigma _{yx}\) takes the

unexpected value \(\pm 4e^{2}/\hslash \left( 2N+1\right) \) on the visible plateaux, i. e., on the first \((N=0)\), second \((N=1)\) and third \((N=3)\) ones. This is an unexpected result

because it does not follow the well-known sequence \(\left( 4e^{2}/\hslash \right) N\), for conventional semiconductors, neither \(\pm 4e^{2}/\hslash \left( N+1/2\right) \) for pristine

graphene and periodic graphene SLs with only a Dirac cone in a weak field9. Thus, the half-integer quantum Hall effect does not occur in Fibonacci GSLs. It should be added that the sequence

\(\pm 4e^{2}/\hslash \left( 2N+1\right) \) was reported in Ref.7 to describe the Hall conductivity steps in periodic graphene SLs with additional Dirac cones. Since such cones do not exist

in the energy spectra of Fibonacci graphene SLs, these arguments can not be invoked here to justify such Hall conductivity values at the mentioned plateaux. It is clear, however, that the

occurrence of these plateaux are a direct consequence of the fractal properties of Fibonacci SLs, in particular, of the existence of two incommensurate periods in them27,29. Further works

are needed for a better understanding of the Hall conductivity values at these plateaux. Finally, a comparison between the results shown in Fig. 4a–c shows that the curves associated with

the chosen fields exhibit a very similar behavior as functions of the scaled chemical potential \(\mu /\hbar \,\omega _C\), where \(\omega _C\sim \sqrt{B}\) is the cyclotron frequency.

Indeed, it is apparent that if these figures are superimposed, such curves essentially coincide in that range of \(\mu /\hbar \,\omega _C\) where the principal plateaux are located, whereas

a slight difference is observed outside it. The latter is due to the overlap of the magnetic subbands. Thus, the Hall conductivity exhibits a self-similar structure for the considered

magnetic fields, which are related by \(\tau ^{2}\) and \(\tau ^{4}\). CONDUCTIVITY IN PERIODIC GSLS. A BRIEF COMPARISON To compare our results with the corresponding ones for periodic GSL,

it is necessary to take into account the properties of its energy spectra for the same parameters as those used above for the Fibonacci GSL, i. e., for barrier height \(V_0/E_F=2\,\pi \) and

magnetic field _B_ such that \(l_B\gg d\), where _d_ is the SL period. It is well known that9,30, for these parameters, the magnetic subbands of the periodic SL are essentially flat,

whereas its band structure in the absence of _B_ only exhibits one Dirac point (cone). Now, since \(\langle i|J_y|i \rangle = \langle n,k_y|J_y|n,k_y \rangle \sim \partial E_n (k_y)/\partial

k_y\) in Eq. (1) and the magnetic subbands are nearly flat, the contribution of the diffusive conductivity to the periodic-SL conductivity can be neglected, in contrast to the contribution

shown in Fig. 1 for the Fibonacci GSL. Further, due to the flat character of the magnetic subbands, the Hall conductivity exhibits well-defined plateaux around the mentioned Dirac point,

with values given by \(\pm (N+1/2)\,4\,e^2/h\) at these plateaux, as shown in Ref.9. These plateaux have the same origin as those shown in our Fig. 4, but the Hall conductivity values

contrast to those of the Fibonacci GSL. SUMMARY AND CONCLUSIONS We have studied the magnetoconductivity properties of Fibonacci GSLs in the presence of a perpendicular magnetic field _B_. It

was shown that the _B_-dependence of the diffusive conductivity exhibits a complicated oscillatory behavior whose charcateristics depend on the range of _B_ considered and cannot be

associated with Weiss oscillations, but rather with Shubnikov–de Haas ones. The absense of Weiss oscillations is attributed to the existence of two incommensurate periods in Fibonacci SLs.

It was also found that the quasiperiodicity of the structure leads to a renormalization of the Fermi velocity \(v_{F}\) of graphene. Our calculations revealed that, for weak _B_, the dc Hall

conductivity \(\sigma _{yx}\) exhibits well defined and robust plateaux as a function of the chemical potential, where it takes unexpected values. It was finally shown that \(\sigma _{yx}\)

displays self-similarity for magnetic fields related by \(\tau ^{2}\) and \(\tau ^{4}\). DATA AVAILABILITY All the files with tables, figures, and codes are available. The corresponding

author will provide all the files in case they are requested. REFERENCES * Novoselov, K. S. _et al._ Electric field effect in atomically thin carbon films. _Science_ 306, 666–669 (2004).

Article  ADS  CAS  Google Scholar  * Novoselov, K. S. _et al._ Two-dimensional gas of massless Dirac fermions in graphene. _Nature_ 438, 197–200 (2005). Article  ADS  CAS  Google Scholar  *

Zhang, Y., Tang, Y.-W., Stormer, H. L. & Kim, P. Experimental observation of the quantum Hall effect and Berrys phase in graphene. _Nature_ 438, 201–204 (2005). Article  ADS  CAS  Google

Scholar  * Gusynin, V. P. & Sharapov, S. G. Unconventional integer quantum Hall effect in graphene. _Phys. Rev. Lett._ 95, 146801 (2005) (4PP). Article  ADS  CAS  Google Scholar  *

Peres, N. M. R., Guinea, F. & Castro Neto, A. H. Electronic properties of disordered two-dimensional carbon. _Phys. Rev. B_ 73, 125411 (2006) (23PP). Article  ADS  Google Scholar  *

McClure, J. W. Diamagnetism of graphite. _Phys. Rev._ 104, 666–671 (1956). Article  ADS  CAS  Google Scholar  * Park, C.-H., Son, Y.-W., Yang, L., Cohen, M. L. & Louie, S. G. Landau

levels and quantum Hall effect in graphene superlattices. _Phys. Rev. Lett._ 103, 046808 (2009) (4PP). Article  ADS  Google Scholar  * Jiang, L. & Zheng, Y. Magnetic miniband and

magnetotransport property of a graphene superlattice. _J. Appl. Phys._ 109, 053701 (2011) (6PP). Article  ADS  Google Scholar  * Wu, S., Killi, M. & Paramekanti, A. Graphene under

spatially varying external potentials: Landau levels, magnetotransport, and topological modes. _Phys. Rev. B_ 85, 195404 (2012) (17PP). Article  ADS  Google Scholar  * Matulis, A. &

Peeters, F. M. Appearance of enhanced Weiss oscillations in graphene: Theory. _Phys. Rev. B_ 75, 125429 (2007) (6PP). Article  ADS  Google Scholar  * Nasir, R., Sabeeh, K. & Tahir, M.

Magnetotransport in a periodically modulated graphene monolayer. _Phys. Rev. B_ 81, 085402 (2010) (10PP). Article  ADS  Google Scholar  * Cheung, A. K. C., Raghu, S. & Mulligan, M. Weiss

oscillations and particle-hole symmetry at the half-filled Landau level. _Phys. Rev. B_ 95, 235424 (2017) (11PP). Article  ADS  Google Scholar  * Kumar, R. K. _et al._ High-temperature

quantum oscillations caused by recurring Bloch states in graphene superlattices. _Science_ 357, 181–184 (2017). Article  ADS  Google Scholar  * Drienovsky, M. _et al._ Commensurability

oscillations in one-dimensional graphene superlattices. _Phys. Rev. Lett._ 121, 026806 (2018) (6PP). Article  ADS  CAS  Google Scholar  * Zarenia, M., Vasilopoulos, P. & Peeters, F. M.

Magnetotransport in periodically modulated bilayer graphene. _Phys. Rev. B_ 85, 245426 (2012) (10PP). Article  ADS  Google Scholar  * Tahir, M. & Vasilopoulos, P. Commensurability

oscillations in a periodically modulated phosphorene. _J. Phys.-Condens. Mat._ 29, 425302 (2017) ((8PP)). Article  CAS  Google Scholar  * Sena, S. H. R., Pereira, J. M. Jr., Farias, G. A.,

Vasconcelos, M. S. & Albuquerque, E. L. Fractal spectrum of charge carriers in quasiperiodic graphene structures. _J. Phys. Condens. Mat._ 22, 465305 (2010) (7PP). Article  ADS  CAS 

Google Scholar  * Yin, Y.-H., Niu, Y.-X., Ding, M., Liu, H.-Y. & Liang, Z.-J. Transport and conductance in Fibonacci graphene superlattices with electric and magnetic potentials. _Chin.

Phys. Lett._ 33, 057202 (2016) ((4PP)). Article  ADS  Google Scholar  * Endo, A. & Iye, Y. Fourier analyses of commensurability oscillations in Fibonacci lateral superlattices. _Phys.

Rev. B_ 78, 085311 (2008) ((10PP)). Article  ADS  Google Scholar  * Charbonneau, M., van Vliet, K. M. & Vasilopoulos, P. Linear response theory revisited III: One-body response formulas

and generalized Boltzmann equations. _J. Math. Phys._ 23, 318–336 (1982). Article  ADS  Google Scholar  * Peeters, F. M. & Vasilopoulos, P. Electrical and thermal properties of a

two-dimensional electron gas in a one-dimensional periodic potential. _Phys. Rev. B_ 46, 4667–4680 (1992). Article  ADS  CAS  Google Scholar  * de Dios-Leyva, M., Hernández-Bertrán, M. A.,

Morales, A. L. & Duque, C. A. Optical absorption in periodic graphene superlattices: Perpendicular applied magnetic field and temperature effects. _Huynh Vinh Phuc, Ann. Phys.-Berlin_

530, 1700414 (2018) (11PP). Article  ADS  MathSciNet  Google Scholar  * Wang, Y. Y. & Maan, J. C. Magnetic levels in quasiperiodic superlattices. _Phys. Rev. B_ 40, 1955–1958 (1989).

Article  ADS  CAS  Google Scholar  * Kolář, M. & Ali, M. K. Generalized Fibonacci superlattices, dynamical trace maps, and magnetic excitations. _Phys. Rev. B_ 39, 426–432 (1989).

Article  ADS  Google Scholar  * de Dios-Leyva, M., Hernández-Bertrán, M. A., Morales, A. L. & Duque, C. A. Quasiperiodic graphene superlattices: Self-similarity of the Landau level

spectra. _Solid State Commun._ 284–286, 93–95 (2018). Article  ADS  Google Scholar  * Tahir, M., Sabeeh, K. & MacKinnon, A. Weiss oscillations in the electronic structure of modulated

graphene. _J. Phys.: Condens. Mat._ 19, 406226 (2007) (7PP). CAS  Google Scholar  * Levine, D. & Steinhardt, P. J. Quasicrystals. I. Definition and structure. _Phys. Rev. B_ 34, 596–616

(1986). Article  ADS  CAS  Google Scholar  * Laruelle, F. _et al._ dsfgsfggf. In _Localization and Confinement of Electrons in Semiconductors_ (eds Kuchar, R. _et al._) 258 (Springer,

Berlin, 1990). Chapter  Google Scholar  * MacDonald, A. H. sdfdffsdfdff. In _Intefaces, Quantum Wells, and Superlattices_ (eds Leavens, C. R. & Taylor, R.) 347 (Plenum, New York, 1987).

Google Scholar  * Duque, C. A., Hernández-Bertrán, M. A., Morales, A. L. & de Dios-Leyva, M. Exploring graphene superlattices: Magneto-optical properties. _J. Appl. Phys._ 121, 074301

(2017) (10PP). Article  ADS  Google Scholar  Download references ACKNOWLEDGEMENTS The authors are grateful for the financial support provided by the Alma Mater Project of the University of

Havana and the Colombian Agencies CODI-Universidad de Antioquia (Estrategia de Sostenibilidad de la Universidad de Antioquia and projects: “Efectos de capas delta dopadas en pozos cuánticos

como fotodetectores en el infrarrojo”, “Propiedades magneto-ópticas y óptica no lineal en superredes de Grafeno”, “Efectos ópticos intersubbanda, no lineales de segundo orden y dispersión

Raman, en sistemas asimétricos de pozos cuánticos acoplados” and “Estudio de propiedades ópticas en sistemas semiconductores de dimensiones nanoscópicas”) and Facultad de Ciencias Exactas y

Naturales-Universidad de Antioquia (CAD exclusive dedication projects 2019-2020). C. A. Duque is grateful to J. H. Ojeda, co-researcher in the project financed by Universidad Pedagógica y

Tecnológica de Colombia (project SGI 2787). The authors also acknowledge the financial support from the Colombian Agency _El Patrimonio Autónomo Fondo Nacional de Financiamiento para la

Ciencia, la Tecnología y la Innovación, Francisco José de Caldas-COLCIENCIAS_ (project: CD 111580863338, CT FP80740-173-2019). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of

Theoretical Physics, University of Havana, San Lázaro y L, Vedado, 10400, Havana, Cuba M. de Dios-Leyva * Grupo de Materia Condensada-UdeA, Instituto de Física, Facultad de Ciencias Exactas

y Naturales, Universidad de Antioquia UdeA, Calle 70 No. 52-21, Medellín, Colombia A. L. Morales & C. A. Duque Authors * M. de Dios-Leyva View author publications You can also search for

this author inPubMed Google Scholar * A. L. Morales View author publications You can also search for this author inPubMed Google Scholar * C. A. Duque View author publications You can also

search for this author inPubMed Google Scholar CONTRIBUTIONS The contributions of the authors are as follows: M.D.-L.: proposed the problem and was responsible of the discussion and writing

of the manuscript. A.L.M.: was responsible of discussions and writing of the manuscript. C.A.D.: were responsible of the numerical calculations and writing of the manuscript. CORRESPONDING

AUTHOR Correspondence to C. A. Duque. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE Springer Nature remains

neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons

Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original

author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the

article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your

intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence,

visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE de Dios-Leyva, M., Morales, A.L. & Duque, C.A. Magnetoconductivity in

quasiperiodic graphene superlattices. _Sci Rep_ 10, 21284 (2020). https://doi.org/10.1038/s41598-020-78479-9 Download citation * Received: 04 March 2020 * Accepted: 12 November 2020 *

Published: 04 December 2020 * DOI: https://doi.org/10.1038/s41598-020-78479-9 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable

link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative