Prediction of hydrogenated group iv–v hexagonal binary monolayers

ABSTRACT Group IV and V monolayers are very crucial 2D materials for their high carrier mobilities, tunable band gaps, and optical linear dichroism. Very recently, a novel group IV–V binary

compound, \({\hbox {Sn}}_2{\hbox {Bi}}\), has been synthesized on silicon substrate, and has shown very interesting electronic properties. Further investigations have revealed that the

monolayer would be stable in freestanding form by hydrogenation. Inspired by this, by means of first-principles calculations, we systematically predict and investigate eight counterparts of

\({\hbox {Sn}}_2{\hbox {Bi}}\), namely \({\hbox {Si}}_2{\hbox {P}}\), \({\hbox {Si}}_2{\hbox {As}}\), \({\hbox {Si}}_2{\hbox {Sb}}\), \({\hbox {Si}}_2{\hbox {Bi}}\), \({\hbox {Ge}}_2{\hbox

{P}}\), \({\hbox {Ge}}_2{\hbox {As}}\), \({\hbox {Ge}}_2{\hbox {Sb}}\), and \({\hbox {Ge}}_2{\hbox {Bi}}\). The cohesive energies, phonon dispersions, and AIMD calculations show that,

similar to \({\hbox {Sn}}_2{\hbox {Bi}}\), all of these freestanding monolayers are stable in hydrogenated form. These hydrogenated monolayers are semiconductors with wide band gaps, which

are favorable for opto-electronic purposes. The \({\hbox {Si}}_2{\hbox {YH}}_2\) and \({\hbox {Ge}}_2{\hbox {YH}}_2\) structures possess indirect and direct band gaps, respectively. They

represent very interesting optical characteristics, such as good absorption in the visible region and linear dichroism, which are crucial for solar cell and beam-splitting devices,

respectively. Finally, the \({\hbox {Si}}_2{\hbox {SbH}}_2\) and \({\hbox {Si}}_2{\hbox {BiH}}_2\) monolayers have suitable band gaps and band edge positions for photocatalytic water

splitting. Summarily, our investigations offer very interesting and promising properties for this family of binary compounds. We hope that our predictions open ways to new experimental

studies and fabrication of suitable 2D materials for next generation opto-electronic and photocatalytic devices. SIMILAR CONTENT BEING VIEWED BY OTHERS NB3CL8: A PROTOTYPICAL LAYERED

MOTT-HUBBARD INSULATOR Article Open access 12 January 2024 THICKNESS AND DEFECT DEPENDENT ELECTRONIC, OPTICAL AND THERMOELECTRIC FEATURES OF \(\HBOX {WTE}_2\) Article Open access 26 July

2022 FIRST-PRINCIPLES INVESTIGATION OF LAMG2NI AND ITS HYDRIDES Article Open access 22 July 2020 INTRODUCTION The high tower of the contemporary technology is built by blocks of silicon and

germanium. Since the successful synthesize of the monolayer carbon (graphene)1 and discovery of its remarkable characteristics, such as high carrier mobility2, strong mechanical parameters3,

and optical transparency4, a great inquiry for other elemental monolayers is in the agenda of many scientists around the world. The monolayers of carbon’s neighbors in group-IV, silicon and

germanium (silicene and germanene) are among the most important predicted and synthesized monolayers beyond graphene5,6. Unlike graphene, which is completely flat with an \({\hbox {sp}}^2\)

bonding characteristics, the larger interatomic distance in silicene and germanene weakens the \(\pi - \pi \) overlaps, which leads to buckled structures with \({\hbox {sp}}^2 - {\hbox

{sp}}^3\) hybrid orbitals. Despite their buckled geometry, silicene and germanene share most of the important electronic features of graphene, such as Dirac cone, high Fermi velocity and

carrier mobility7,8, with some advantages including better tunability of the band gaps9, stronger spin-orbit coupling10, and easier valley polarization11, which are very important for

electrics, spintronics, and valleytronics. On the other hand, monolayers of group-V elements, known as pnictogens, including phosphorene, arsenene, antimonene, and bismuthene, recently have

gained much attention for their topological aspects, as well as inherent, wide, and tunable band gaps12,13,14,15. Generally, several allotropes are considered for these monolayers, including

\(\alpha \) (puckered or washboard) and \(\beta \) (buckled honeycomb or graphene-like), as the most important and stable phases. For arsenene, antimonene, and bismuthene, the \(\beta

\)-phase, and for phosphorene, the \(\alpha \)-phase is more stable in aspects of energetics and phonon dispersions12,16. The \(\alpha \)-phase phosphorene and arsenene possess direct band

gaps, while their \(\beta \) counterparts have indirect ones. On the other hand, antimonene and bismuthene respectively have indirect and direct band gaps in both phases. These band gaps are

within a wide range of 0.36 (for \(\alpha \)-bismuthene) to 2.62 eV (for \(\beta \)-phosphorene)13,14,15. Moreover, phosphorene, arsenene, and bismuthene possess carrier mobilities as high

as several thousand \({\text{ cm}}^2 {\text{ V}}^{-1} {\text{s}}^{-1}\)12. These exciting properties makes group-V monolayers very favorable candidates for optoelectronics, and

photocatalytic devices. Because of high ratio between the surface and thickness of 2D structures, effects of chemical functionalization play an important role in tuning their properties.

Hence, in addition to pure elemental monolayers, 2D materials with functionalized structures gained attention for expanding the scope of realized physical aspects and enhancing potential

applications. These efforts include designing and applying various types of heterostructures17, defections18, vacancies19, adsorptions20, and compounds21,22. Among these, binary compounds

have the advantage of relatively easier fine control of the growth dynamics and more feasible fabrication. They could represent unusual atomic configuration and chemical stoichiometry23

which leads to extraordinary physical properties for future applications and opening ways to new researches. As an example of group IV-V binary compound, Barreteau et al have succeed to

synthesize the bulk single crystals of layered SiP, SiAs, GeP, and GeAs by melt-growth method. They showed that these layered materials all exhibit semiconducting behavior, and suggest that

they can be further exfoliated into 2D structures24. Moreover, a number of recent theoretical works were performed on group IV-V 2D binary compounds and reported interesting results in

thermoelectricity for SiX (\({\hbox {X}}={\hbox {N}}\), P, As, Sb, and Bi)25, visible-light photohydrolytic catalysts for SiP26, strain-tunable electron mobility for XY (\({\hbox {X}} =

{\hbox {C}}\), Si, and Ge, and \({\hbox {Y}} = {\hbox {N}}\), P, and As)27, and ORR applications in novel fuel cells for metal (Ni, Pd, Pt, and Ru) complexes in graphene basal planes28. Very

recently, Gou et al. have synthesized a unique hexagonal 2D binary compound, \({\hbox {Sn}}_2{\hbox {Bi}}\), on a silicon (111) substrate which exhibits strong spin-orbit coupling and high

electron-hole asymmetry23. In the band structure of this semiconducting monolayer, electron flat bands and free hole bands are seen which are indicatives of nearly free and strongly

localized charge carriers. Moreover, this monolayer is very stable because all the Si, Bi, and Sn atoms satisfy the octet rule. These features make \({\hbox {Sn}}_2{\hbox {Bi}}\) a good

candidate for nano-electronics and may result in nontrivial properties like ferromagnetism29 and superconductivity30. Furthermore, the synthesis of other group-IV-V \({\hbox {X}}_2{\hbox

{Y}}\) counterparts of \({\hbox {Sn}}_2{\hbox {Bi}}\) was proposed by Gou et al23. Generally, experimental synthesis of yet unknown systems can be guided by predictive theoretical

first-principles calculations which distinguish stable and unstable structures correctly. In other words, theoretical predictions play an important role in progress of materials science and

technology, by means of justifying the cost and effort of potential experiments. Many advances in materials science have been conducted and inspired by earlier theoretical investigations.

Most of the presently well-known synthesized 2D materials, such as borophene31, stanene, germanene, silicene7, arsenene13, antimonene14, bismuthene15, etc. were firstly predicted by

theoretical studies which brought sufficient motivations for experimental work. Herein, inspired by the successful deposition of \({\hbox {Sn}}_2{\hbox {Bi}}\) monolayer, as well as the

importance of group IV and V monolayers, we predicted a new family of binary compound monolayers with a hexagonal structure and an empirical formula of \({\hbox {X}}_2{\hbox {Y}}\), where X

and Y are respectively chosen from group-IV (Si and Ge) and V (P, As, Sb, and Bi), namely \({\hbox {Si}}_2{\hbox {P}}\), \({\hbox {Si}}_2{\hbox {As}}\), \({\hbox {Si}}_2{\hbox {Sb}}\),

\({\hbox {Si}}_2{\hbox {Bi}}\), \({\hbox {Ge}}_2{\hbox {P}}\), \({\hbox {Ge}}_2{\hbox {As}}\), \({\hbox {Ge}}_2{\hbox {Sb}}\), and \({\hbox {Ge}}_2{\hbox {Bi}}\). We firstly stabilize the

mentioned monolayers by hydrogenation, and further check their stability by cohesive energy, molecular dynamics, and phonon dispersion analysis, and interpret their phonon modes and

thermodynamical properties. Furthermore, we analyze their electronic and optical properties and discuss their potential strengths. Eventually, we consider these semiconductors for

photocatalytic purposes and check their potential applications in water-splitting. Our results suggest that these monolayers are strongly applicable in a very vast areas such as

valleytronics, opto-electronics, beam-splitters, optical detectors, and water-splitters. Moreover, the structural similarity with the synthesized \({\hbox {Sn}}_2{\hbox {Bi}}\) monolayer,

promises the possibility of their deposition on proper substrates and brings hopes for advances in technological devices. COMPUTATIONAL DETAILS The first-principles calculations were

performed based on the density functional theory (DFT), as implemented in the Quantum Espresso package32. During the entire calculations, the norm-conserving (NC) pseudo-potentials with a

plane wave basis set were employed to describe the electron wave functions. The generalized gradient approximation (GGA) was used with the formulation of Perdew–Burke–Ernzerhof (PBE) to

describe the exchange-correlation potential33. Because the GGA usually underestimates the band gaps, the HSE06 hybrid functional was also used to obtain more accurate band gaps. The energy

cut-off for wave function and charge density was set to 50 and 300 Ry, respectively. The Monkhorst-Pack scheme was used to sample the Brillouin zone with a \(13 \times 13\times 1 \) and \(21

\times 21\times 1\) k-points for geometric optimization and electronic calculations, respectively. However, for the HSE calculations, the k-points was set to be \(5 \times 5\times 1 \). A

vacuum space of 20 Å was chosen along the z-direction to prevent spurious interactions between layers in the periodic boundary condition. All the monolayers were fully relaxed with a force

and stress tolerance of 10\(^{-3}\) eV/Å and 10\(^{-4}\) GPa, respectively. To calculate the phonon dispersion, the finite displacement method was adopted, in which a \(3 \times 3\times \)1

supercell with a \(5 \times 5\times \)1 k-point sampling was built. To investigate the optical properties, the frequency-dependent dielectric function was calculated within the independent

particle approximation (IPA) which describes single-particle excitations, as implemented in the epsilon code inbuilt in the QE package. The calculation was performed by means of

self-consistent ground-state eigenvalues and eigenfunctions. To determine the structural stability of the monolayers, their cohesive energies (\(E_c\)) were calculated using the equation

below: $$\begin{aligned} E_c=\frac{E_{sheet}-\sum _{i} n_i E_{atom-i}}{N} \end{aligned}$$ (1) where \(E_{sheet}\) and \(E_{atom-i}\) stand for total energy of the sheet and the isolated

atom-i with considerations of the spin polarization, respectively. _N_ and \(n_i\) are the numbers of total atoms and atom-i in the unit cell, respectively. To check the thermal stability,

the ab-initio molecular dynamics (AIMD) simulations were performed using NVT canonical ensemble at room temperature (300 K). The initial model was constructed by a \(3 \times 3\times \)1

supercell for minimizing the constraint caused by periodicity. Here, the total simulation time was set to be 4.0 ps with time steps of 2.0 fs. RESULTS AND DISCUSSION STRUCTURAL STABILITY AND

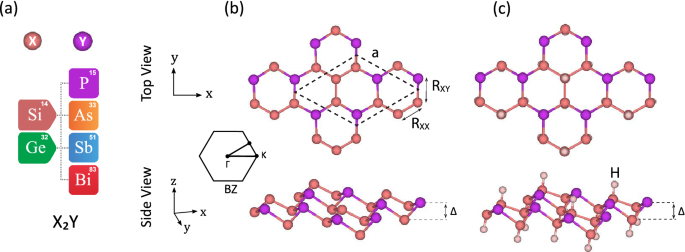
PHONON CALCULATIONS The graphene-like structure was used to construct eight new binary monolayers, with a threefold-coordinated X (Si and Ge) and Y (P, As, Sb, and Bi) atoms in a hexagonal

unit cell containing six atoms, as shown in Fig. 1. Through the structural optimization with the GGA-PBE exchange-correlation, the relaxed lattice constants and bond lengths were calculated

in the range of 6.33 to 7.23 Å and 2.26 to 2.75 Å, respectively. All the relaxed monolayers have buckled structures with buckling heights in the range of 0.86 to 1.24 Å in which the longer

atomic radius creates larger buckling heights. Moreover, all of the monolayers represent metallic electronic properties. The calculated structural parameters are available in the Supporting

Information, Table S1. The X and Y atoms have \(\hbox {ns}^2\) \(\hbox {np}^2\) (\(\hbox {n} = 3, 4\)) and \(\hbox {ns}^2\) \(\hbox {np}^3\) (n = 3–6) outer shell electron configurations,

respectively. Therefore, when they form a threefold configuration, the octet rule only fulfills for the Y, not X atoms. Thus, these pure structures are predicted to be unstable in a

freestanding configuration. Phonon dispersion analyses confirm that these monolayers are dynamically unstable (Fig. S1). The same instability has also been reported for freestanding \(\hbox

{Sn}_2\hbox {Bi}\) monolayer while it can be greatly stabilized by hydrogenation34,35. Hydrogenation is a well-recognized technique for stabilization and tuning the physical characteristics

of nano-scale systems. Many experimental studies have been done on performing different methods of hydrogenation. For example, the surface hydrogenated graphene (aka graphane) was prepared

by exposure of graphene to a cold hydrogen plasma which led to the opening of a band gap and other changes in its electronic properties36. This success was inspired by previous theoretical

predictions which conducted the experiment well into a new graphene-based structure37,38. In addition, several phases of borophene have been synthesized on Ag (111), Au (111), and Cu (111)

substrates, which are metal and unstable in freestanding form. Eventually, a new phase of hydrogenated borophene was synthesized by thermal decomposition of sodium borohydride (\(\hbox

{NaBH}_4\)) powders, which shows an ultra-stability and semi-conducting characteristics in the air environment39. This achievement was also led by theoretical predictions40. In our case, the

\(\hbox {Sn}_2\hbox {Bi}\) monolayer was firstly synthesized on a silicon substrate23. Subsequently, a computational study suggested that the isolated \(\hbox {Sn}_2\hbox {Bi}\) is a metal

which suffers from instability due to the dangling bonds. However, it can become a stable semiconductor by use of chemical functionalization, such as surface hydrogenation34. By comparison,

it is found that the results of hydrogenated \(\hbox {Sn}_2\hbox {Bi}\) are very similar to that of \(\hbox {Sn}_2\hbox {Bi}\) synthesized on the substrate. For example, in both systems,

there are electron flat bands and free hole bands, which provide the possibility of having strongly localized electrons and free holes. Also, the bandgap predicted for hydrogenated \(\hbox

{Sn}_2\hbox {Bi}\) is 0.92 eV which agrees well with bandgap of 0.8 eV for substrate-supported monolayer revealed by angle-resolved photoemission spectroscopy measurements23,34. In the

following, we show that the predicted \(\hbox {X}_2\hbox {Y}\) monolayers, similar to \(\hbox {Sn}_2\hbox {Bi}\), can be stabilized and become semiconductors by surface hydrogenation. In

other words, we found an interesting analogous trend shared with \(\hbox {Sn}_2\hbox {Bi}\) and its eight counterparts suggested by us. Summarily, according to similarity of \(\hbox

{Sn}_2\hbox {BiH}_2\) and \(\hbox {Sn}_2\hbox {Bi/Si}\)(111)23,34, we predict that the properties of the hydrogenated \(\hbox {X}_2\hbox {Y}\) monolayers are also similar to possible

deposited monolayers on suitable insulator substrates such as ZnS (111), SiC (111), and Si(111). For surface hydrogenation, we investigated both single and double side hydrogenated

structures, where hydrogen make bonds with X (Si and Ge) atoms, so the octet rule would be fulfilled. According to the cohesive energies, the double side hydrogenated model, having the

lowest ground state energy, is predicted to be the most stable structure. Therefore, we denote the rest of the investigations to this model which is described in Fig. 1c. In the following,

we further confirm their structural, thermal and dynamical stability by means of cohesive energy, molecular dynamics, and vibrational phonon analysis. Table 1 lists the structural and

electronic parameters for these monolayers. Lattice constants, bond lengths, and buckling heights are in the range of 6.26 to 7.18 Å, 2.27 to 2.75 Å, and 1.08 to 1.38 Å, respectively. As can

be seen, hydrogenation causes an increase in buckling heights and a decrease in lattice constants for all the monolayers, which is due to the strong bonds between H and X atoms. Similar

behaviors have also been reported for hydrogenation and fluorination of penta-graphene41, silicene42, germanene43, and stanene44. We have also performed the ab-initio molecular dynamics

(AIMD) simulations to verify the thermal stability of the \(\hbox {X}_2\hbox {YH}_2\) binary compounds. Figure 3 exhibits the fluctuations of potential energy and evolutions of geometric

structure of the \(\hbox {Ge}_2\hbox {BiH}_2\) monolayer during the simulations at 300 K. As can be seen, the potential energy oscillates with an extent of less than 0.4 eV/atom, and no

obvious structural distortions are found, indicating that the \(\hbox {Ge}_2\hbox {BiH}_2\) is thermally stable at 300 K. The thermal stability of the \(\hbox {Ge}_2\hbox {BiH}_2\)

guarantees stability of all the predicted structures because it has the highest cohesive energy among them (see Fig. 2). Indeed, this suggests that the \(\hbox {X}_2\hbox {YH}_2\) binary

compounds can be realized experimentally at room temperature (Fig. 3). To further confirm the stability of the hydrogenated monolayers, the phonon dispersion spectra were calculated and

displayed in Fig. 4. It is clear that there is no imaginary frequency in the whole Brillouin zone, which confirms that these freestanding monolayers are dynamically stable. The spoon-shaped

curves near the \(\Gamma \) point do not mean instability, but they are signatures of the flexural acoustic modes, which are usually hard to converge in 2D sheets. These soft modes are also

found in other analogous systems45,46. All the phonon spectra have rather similar trends, which mean similar bonding. Also, it is clear that the maxima of acoustic modes decline with going

down in group IV and V where \(\hbox {Si}_2\hbox {PH}_2\) and \(\hbox {Ge}_2\hbox {BiH}_2\) display the highest (100 \(\hbox {cm}^{-1}\)) and lowest (38 \(\hbox {cm}^{-1}\)) peaks. Based on

these maxima, the Debye temperatures are obtained by \(\theta _D=h\nu _m/K\!_B\)47, where _h_ and \(K\!_B\) are the Planck and Boltzmann constants, respectively. The calculated temperatures

are in the range of 143 to 54 K (listed in Table 1) which are lower than graphene (2266 K), silicene (798 K), phosphorene (206 K), arsenene (170 K), and comparable to antimonene (101 K),

bismuthene (50 K), and stanene (72 K)47,48,49,50. Such low Debye temperatures and large buckling heights, which are indicatives of low lattice thermal conductivity, may bring hope for these

monolayers to be suitable candidates for thermoelectric applications. Interestingly, the slope of the parabolic out-of-plane acoustic mode (ZA) near the \(\Gamma \) point (specified in Fig. 

4) decreases with increasing of the average atomic mass of the monolayers. This will bring a slower phonon group velocity, subsequently lower lattice thermal conductivity, and stronger

anharmonicity, especially for \(\hbox {Si}_2\hbox {BiH}_2\), \(\hbox {Ge}_2\hbox {AsH}_2\), \(\hbox {Ge}_2\hbox {SbH}_2\), and \(\hbox {Ge}_2\hbox {BiH}_2\). It is worth noting that the ZA

mode has a high contribution to the phonon transport51. On the other hand, the hybridization of the optical and acoustic phonon branches increases the phonon scattering which reveals low

phonon transport. These behaviors represent the possible potential of \(\hbox {X}_2\hbox {YH}_2\) monolayers in thermoelectricity. According to Eq. (1), the more negative values for cohesive

energies suggest more structural stability for the monolayers. As shown in Table 1, the cohesive energies vary from − 3.88 eV/atom for \(\hbox {Si}_2\hbox {PH}_2\) to − 3.08 eV/atom for

\(\hbox {Ge}_2\hbox {BiH}_2\) which indicates that all of the monolayers are stable. In fact, the structures represent more stability when the atoms are lighter. By comparison, one can

easily realize that all the predicted monolayers are more stable than the hydrogenated \(\hbox {Sn}_2\hbox {Bi}\) (\(\hbox {Sn}_2\hbox {BiH}_2\)), which was discussed in our previous study

to have a cohesive energy of − 2.95 eV/atom35. Also, the \(\hbox {Si}_2\hbox {SbH}_2\), \(\hbox {Si}_2\hbox {BiH}_2\), \(\hbox {Ge}_2\hbox {SbH}_2\), and \(\hbox {Ge}_2\hbox {BiH}_2\)

monolayers are more stable than SiSb (− 3.50 eV/atom), SiBi (− 3.31 eV/atom), GeSb (− 3.12 eV/atom), and GeBi (− 2.98 eV/atom) binary compounds, respectively. The rest have appreciable

cohesive energies comparable to SiP (− 4.19 eV/atom), SiAs (− 3.85 eV/atom), GeP (− 3.60 eV/atom), and GeAs (− 3.36 eV/atom)52. All the mentioned cohesive energies above were calculated

through GGA-PBE functional. For a better comparison between cohesive energies of the predicted binary compounds, please pay attention to Fig. 2. Phonon dispersion is also a key to calculate

thermodynamic properties of a system. For example, the constant volume heat capacity, \(C_V\) is defined as53: $$\begin{aligned} C_V=\sum _{s,q}K\!_B\left( \frac{\hslash \omega

_s(q)}{K\!_BT}\right) ^2 \frac{exp(\hslash \omega _s(q)/K\!_BT)}{\left( exp(\hslash \omega _s(q)/K\!_BT)-1\right) ^2} \end{aligned}$$ (2) where \(\hslash \) is the reduced Planck’s constant,

and \(\omega _s(q)\) is the frequency of the _s_ phonon branch at the _q_ point. According to the Debye model, in the high-temperature limit, i.e. \(K\!_BT \gg \hslash \omega \), the heat

capacity simply approaches to the classical Dulong-Petit results, which is \(3N\!M\!K\!_B\), where _N_ is the number of atoms in the unit cell and _M_ is the number of unit cells in a

crystal (\(\approx \) 24.94 J \(\hbox {mol}^{-1}\) \(\hbox {K}^{-1}\) for one mole of a mono-atomic solid)54. Figure 5 exhibits the \(C_V\) calculated for the hydrogenated binary compounds

as a function of temperature (one mole, divided by the number of atoms in the unit cell) which was calculated by use of the phonon dispersion spectra. As it is clear, the \(C_V\) is

converged to \(\sim \) 24 J \(\hbox {mol}^{-1}\) \(\hbox {K}^{-1}\) in high-temperature limit, which is in good agreement with the Debye model. Moreover, the \(C_V\) for \(\hbox {Si}_2\hbox

{PH}_2\), \(\hbox {Si}_2\hbox {AsH}_2\), \(\hbox {Si}_2\hbox {SbH}_2\), \(\hbox {Si}_2\hbox {BiH}_2\), \(\hbox {Ge}_2\hbox {PH}_2\), \(\hbox {Ge}_2\hbox {AsH}_2\), \(\hbox {Ge}_2\hbox

{SbH}_2\), and \(\hbox {Ge}_2\hbox {BiH}_2\), at room temperature (300 K) are 15.45, 16.09, 16.57, 16.93, 17.18, 17.71, 18.03, and 18.22 J \(\hbox {mol}^{-1}\) \(\hbox {K}^{-1}\),

respectively (see Table 1). Despite the importance of the \(C_V\) in the understanding of thermal properties, it has not gained sufficient attention in 2D materials so far. To the best of

our probe, some examples of similar calculations are: 23.1 (TiSeS), 22.7 (TiTeS), 22.5 (TiSeTe), 17.5 (\(\hbox {CuTe}_2\hbox {O}_5\)), 11.5 (borophene) J \(\hbox {mol}^{-1}\) \(\hbox

{K}^{-1}\)53,55,56, which are comparable with our results. It is provable that heavier materials have a greater \(C_V\) at room temperature, i.e. they are more resistant to temperature

increase. Therefore, one may conclude that compared with borophene, all of the predicted binary compounds, and compared with \(\hbox {CuTe}_2\hbox {O}_5\), the \(\hbox {Ge}_2\hbox {AsH}_2\),

\(\hbox {Ge}_2\hbox {SbH}_2\), and \(\hbox {Ge}_2\hbox {BiH}_2\) monolayers are better electronic devices in the aspects of not overheating. With confirming the structural stability and

discussing the thermodynamical characteristics, now we turn our attention into the electronic properties of the predicted binary compounds. ELECTRONIC PROPERTIES The electronic band

structures of \(\hbox {X}_2\hbox {YH}_2\) binary compound monolayers have been presented at the GGA and HSE06 levels in Fig. 6. As can be seen, all the monolayers are semiconductors. The

\(\hbox {Ge}_2\hbox {YH}_2\) monolayers have direct band gaps at the \(\Gamma \) point. In contrast, the \(\hbox {Si}_2\hbox {YH}_2\) monolayers have indirect band gaps where their valence

band maxima (VBM) are located at the \(\Gamma \) point and their conduction band minima (CBM) are located at the M (for \(\hbox {Si}_2\hbox {PH}_2\) and \(\hbox {Si}_2\hbox {AsH}_2\)) and K

(for \(\hbox {Si}_2\hbox {SbH}_2\) and \(\hbox {Si}_2\hbox {BiH}_2\)) points, which are identical at both GGA and HSE levels. The band gaps predicted at the HSE level are in the range of

1.57 to 3.19 eV, where \(\hbox {Si}_2\hbox {PH}_2\) and \(\hbox {Ge}_2\hbox {BiH}_2\) exhibit the largest and smallest values, respectively (see Table 1). It is obvious that the band gaps

decrease regularly with increasing the average atomic mass, which is rather common in 2D semiconductors45,52. For example, in group V binary compound monolayers, studied by Zhang et al, the

PAs and SbBi monolayers indicate the largest (2.55 eV) and smallest (1.41 eV) band gaps, respectively. In more details, the reported band gaps are in the order of PAs > PSb > PBi >

AsBi > SbBi57. All the calculated band structures demonstrate parabolic valence bands centered at the \(\Gamma \) point which provides high hole conductivity. Among these, the \(\hbox

{Ge}_2\hbox {YH}_2\) structures have parabolic conduction bands centered at \(\Gamma \) point, which indicate free electrons, while the \(\hbox {Si}_2\hbox {YH}_2\) structures have nearly

flat conduction bands along the K − M direction, which are signatures of localized electrons. In other words, the \(\hbox {Si}_2\hbox {YH}_2\) structures have both free and strongly

localized charge carriers like the \(\hbox {Sn}_2\hbox {Bi}\) monolayer deposited on the silicon substrate23. This high electron-hole asymmetry enforces the materials to exhibit completely

different optical and thermoelectric behavior in the n-type and p-type doping. In addition, all the monolayers have some conduction band extrema (CBE) near the CBM at high symmetry points M,

\(\Gamma \), and K which may be favorable for an n-type Seebeck coefficient58. These CBEs may approach each other by mechanical strain to achieve band convergence59. The band convergence

improves electrical conductivity without affecting other transport coefficients. These features would make the \(\hbox {X}_2\hbox {YH}_2\) monolayers possible candidates for thermoelectric

applications. We also took into account the spin-orbit coupling (SOC) interaction in the calculation of the GGA band structures (SOGGA) as presented in Fig. S2. It can be seen that

consideration of the SOC, more or less, terminates the degeneracy between energy bands and narrows the band gaps. Due to the stronger spin-orbit interactions for heavier atoms, the band

splitting increases as the compounds are heavier. Summarily, the effect of SOC on the band gaps is smaller than 0.3 eV for most of the monolayers, except for relatively heavy \(\hbox

{X}_2\hbox {BiH}_2\) (\(\hbox {Si}_2\hbox {BiH}_2\) & \(\hbox {Ge}_2\hbox {BiH}_2\)) which have SOGGA band gaps approximately 0.5 eV smaller than that of GGA. Overall, for its small

influence on most of the monolayers, the SOC was not considered for the rest of our calculations. Figure 7 shows the total and orbital projected density of states of the hydrogenated binary

monolayers. It can be seen that in the whole energy range, the p orbitals are dominant and the s orbitals have negligible proportions in the electronic characteristics, which was predictable

according to the electronic arrangement of the contained atoms. This domination have been reported for other group IV and V 2D structures13,14,60,61. As it is clear, for all the monolayers,

the Y-p orbitals are dominant in the valance bands, and major peaks around − 2 eV are raised by them. These are attributed to the rather flat bands around − 2 eV in the band structures (see

Fig. 6). On the other hand, the conduction bands are slightly dominated by Si atom for the Si contained structures, while for the Ge contained ones, Ge-p and Y-p orbitals share rather equal

proportions of the conduction band states. Also, more or less, we see an overlapping of DOS of X-p and Y-p orbitals near the Fermi energy for all the monolayers, which are signatures of

strong covalent bonds between the atoms, due to the orbitals hybridization. As can be seen, orbitals hybridization is rather similar for all the compounds in the valance bands, but in the

conduction bands, it is not significant for \(\hbox {Si}_2\hbox {PH}_2\) and \(\hbox {Si}_2\hbox {AsH}_2\). More interestingly, in the Ge contained compounds, the Y-s orbitals also

participate in the hybridization. Orbitals hybridization between different atoms was also reported for other structures such as \(\hbox {Sn}_2\hbox {Bi}\), \(\hbox {C}_3\hbox {N}\), \(\hbox

{C}_3\hbox {P}\), and \(\hbox {C}_3\hbox {As}\) compounds34,62. Moreover, the H atoms have a very limited contribution in the DOS, which means that electrons are strongly bound to them and

do not construct many states in the valance and conduction bands. Namely, a very small hybridization with Y-s orbitals, and no interfere with X orbitals is seen, which suggests ionic bonds

between the H and X atoms. To shed more light on the electronic properties and bonding mechanism of the compounds, electron density (_n_(_r_)), electron difference density (\(\delta n(r)\)),

and electron localization function (ELF) were calculated at the GGA level. Our calculations display that all the monolayers have similar characteristics, therefore, we only present the

analyses for \(\hbox {Si}_2\hbox {SbH}_2\) monolayer, as a representative, in Fig. 8. Analyses for the rest of the monolayers are available in Fig. S3–S5. It is clear from Fig. 8a, that the

lattice has a minimum uniform electron density of about 0.3 e Å\(^{-3}\) which exhibits an in-plane isotropic lattice in aspects of electronic characteristics. It is obvious from _n_(_r_)

and \(\delta n(r)\) (Fig. 8b,c) that there is a gentle electron accumulation between Sb and Si atoms. Moreover, the ELF (Fig. 8d) indicates a high localization between these atoms.

Therefore, one could conclude that the Sb and Si atoms share electrons mutually and make covalent bonds. Meanwhile, there is a high electron density and accumulation on the H, with

significant electron depletion around Si atoms. Besides, the ELF displays the highest localization on the H and a low localization around the Si atoms. Therefore, it is deducible that the H

atoms make ionic bonds with Si atoms. This approves our discussion about the low contribution of H related electrons in the density of states. Also, the strong ionic bonds make sense about

the stability of the monolayers after hydrogenation. In other words, the hydrogenation somehow plays the role of a substrate for the originally unstable pristine monolayers and stabilizes

them. OPTICAL PROPERTIES High optical absorption in 2D materials brings hopes for energy harvesting purposes such as solar cells. Moreover, linear dichroism is a phenomenon widely reported

for 2D materials, which is the difference between optical absorption for light beams polarized parallel and perpendicular to an orientation axis, and is a key element for interesting optical

applications such as beam splitters, LCDs, half-mirrors, etc.63,64. For instance, it is reported that Sb and As monolayers have optical absorption edges near \(\sim \) 2 and \(\sim \) 3 eV

, for perpendicular and parallel polarizations, respectively64. As mentioned in the previous section, the \(\hbox {X}_2\hbox {YH}_2\) binary compounds were predicted to have hopeful signs of

optical potentials, such as wide band gaps in the range of visible light. In this section, we calculate and discuss the optical properties of these monolayers to extract more physical

insights and possible applications. The optical properties are associated with the interactions between light, electrons, and ions in the materials, which should be explained through the

complex dielectric function, \(\epsilon (\omega )=\epsilon _1(\omega )+i\epsilon _2(\omega )\). Based on Fermi’s golden rule, one can derive the imaginary part of the dielectric function as

below65: $$\begin{aligned} \epsilon _2(\omega )=\frac{4\pi ^2e^2}{m^2\omega ^2}\sum _{C,V}\left| P_{C,V} \right| ^2\delta \left( E_C - E_V - \hslash \omega \right) \end{aligned}$$ (3) where

_e_ is the electron charge, _m_ is the electron effective mass, _P_ is the momentum transition matrix, and _E_ is the electron energy level. Moreover, _C_ and _V_ indices stand for

conduction and valance bands, respectively. No need to explain, \(\delta (x-x_0)\) is the Dirac delta function, which ensures conversion of energy during electron transitions from band to

band. This means that every excited state has an infinite lifetime, i.e. is stationary66. Subsequently, the real part can be calculated through Kramer-Kronig relation:67 $$\begin{aligned}

\epsilon _1(\omega )=1+\frac{2}{\pi }\int _{0}^{\infty }\frac{\omega '\epsilon _2(\omega ')}{\omega '^2-\omega ^2}d\omega \end{aligned}$$ (4) Moreover, based on the real and

imaginary parts, the optical absorption coefficient, \(\alpha (\omega )\), is calculated through: $$\begin{aligned} \alpha (\omega )=2\frac{\omega }{c}\sqrt{\frac{\sqrt{\epsilon

_1^2+\epsilon _1^2}-\epsilon _1}{2}} \end{aligned}$$ (5) where _c_ is the speed of light. For the isotropy of the monolayers in the xy plane, there is no significant difference between xx

and yy polarizations, therefore the calculations were performed for polarized radiations, parallel (\(\hbox {E}^\parallel \)) and perpendicular (\(\hbox {E}^\perp \)) to the incidence

direction (z-direction). Figure 9 shows the calculated optical properties of the \(\hbox {X}_2\hbox {YH}_2\) binary compounds, including real and imaginary parts of the dielectric function

(\(\epsilon _1\) and \(\epsilon _2\)), and the absorption coefficient (\(\alpha \)), for both polarizations. Interestingly, the predicted monolayers can be separated into two groups,

group-A, including \(\hbox {Si}_2\hbox {PH}_2\), \(\hbox {Si}_2\hbox {AsH}_2\), \(\hbox {Si}_2\hbox {SbH}_2\), and \(\hbox {Ge}_2\hbox {PH}_2\), and group-B including \(\hbox {Si}_2\hbox

{BiH}_2\), \(\hbox {Ge}_2\hbox {AsH}_2\), \(\hbox {Ge}_2\hbox {SbH}_2\), and \(\hbox {Ge}_2\hbox {BiH}_2\). The materials in each group exhibit similar properties, which will be discussed in

detail. As we know, negative values in the real part of the dielectric function stand for metallic reflectivity68. As it is clear in Fig. 9 (left panel), group-A monolayers have significant

negative values in the real part of the dielectric function within \(\sim \) 3.6 to 8 eV (\(\sim \) 345 to 155 nm) in the UV region, for perpendicular polarized radiation (\(\hbox {E}^\perp

\)). On the contrary, group-B monolayers have significant negative values within \(\sim \) 6.8 to 9.5 eV (\(\sim \) 180 to 130 nm), for parallel polarized radiation (\(\hbox {E}^\parallel

\)). In other words, group-A and group-B materials are metallic for \(\hbox {E}^\perp \) and \(\hbox {E}^\parallel \) UV radiation, within the mentioned ranges, respectively. This means that

group-A and group-B monolayers have a good complement in blocking the UV radiation and may be used together as a heterostructure for more efficient beam splitting, and UV protection

purposes. Compared with the Si and Ge monolayers, which have been reported to have a metallic characteristics in the range of \(\sim \) 4 to 7 eV (310 to 177 nm) and \(\sim \) 0 to 4 eV

(\(\infty \) to 310 nm), respectively44,69, most of the predicted \(\hbox {X}_2\hbox {YH}_2\) binary compounds have better UV blocking. For more details, please see Table 2. The imaginary

part of the dielectric function and the absorption coefficient are bound to each other and should be analyzed together. Based on the band to band transition theory, the peaks in the

imaginary part of the dielectric function are concerned with energy absorption and direct transitions of electrons between bands below and above the Fermi level. As can be seen in Fig. 9

(middle panel), all the monolayers have major peaks around \(\sim \) 3.5 and \(\sim \) 7 eV for \(\hbox {E}^\perp \) and \(\hbox {E}^\parallel \) polarizations, respectively. Moreover, in

group-A monolayers, the \(\hbox {E}^\perp \) peaks are much stronger than the \(\hbox {E}^\parallel \) peaks, whereas, in group-B monolayers, they are relatively equal. This would be

representative of the difference, and equality of significant absorption ranges (\(\alpha \ge 10^{7} m^{-1}\)) between \(\hbox {E}^\perp \) and \(\hbox {E}^\parallel \) polarizations, for

group-A and group-B monolayers, respectively. In other words, as it is shown in Fig. 9 (right panel), group-B monolayers have relatively wider significant absorption ranges for \(\hbox

{E}^\parallel \) polarizations, which is due to the stronger \(\hbox {E}^\parallel \) peaks in the imaginary part of the dielectric function. The widest significant absorption range belongs

to \(\hbox {Si}_2\hbox {BiH}_2\), which is in the range of 2.36 to 12.4 eV (525 to 100 nm). For comparison, it should be noted that the Si and Ge monolayers have significant optical

absorption in the range of \(\sim \) 3.5 to 5 eV (354 to 248 nm) and \(\sim \) 3 to 6 eV (413 to 206.6 nm), respectively44,69. Our calculations show that most of the predicted compounds have

greatly wider significant absorption ranges. For more details about the optical properties, please note to Table 2. Summarily, one can conclude that group-A monolayers, having stronger

linear dichroism, have more potential applications in beam splitting, and group-B monolayers, having a wider absorption range for both polarizations, are more favorable for energy harvesting

systems and solar cells. It should be added that three of group-B monolayers, namely \(\hbox {Ge}_2\hbox {AsH}_2\), \(\hbox {Ge}_2\hbox {SbH}_2\), and \(\hbox {Ge}_2\hbox {BiH}_2\) have

direct and wide band gaps, which makes them even more ideal for this purpose. PHOTOCATALYTIC PROPERTIES Water splitting is a chemical reaction in which the water molecule is broken down into

oxygen and hydrogen. This process has attracted much attention because of clean, inexpensive, and environment friendly production of hydrogen. One of the well-known methods for water

splitting is photocatalysis by use of a semiconductor sheet and solar energy70. The general chemical formula for this reaction is presented as71: The first half reaction shows the water

oxidation at the anode and the second one indicates the water reduction at the cathode. The overall process results in production of hydrogen and oxygen gases as illustrated in Fig. 10. A

semiconductor could be a potential photocatalyst for water splitting if the CBM energy is higher than the reduction potential of \(\hbox {H}^+/\hbox {H}_2\), and the VBM energy is lower than

the oxidation potential of \(\hbox {O}_2/\hbox {H}_2\hbox {O}\)72. It should be noted that there are not many photocatalysts that meet all of the requirements, so far. Therefore, finding a

suitable candidate semiconductor for this purpose is a crucial challenge, that we are going to face in this section. $$ \begin{aligned} & 2{\text{H}}_{2} {\text{O}}_{{({\text{Liquid}})}}

+ 4{\text{h}}^{ + } \to 4{\text{H}}^{ + } + {\text{O}}_{{2({\rm {gas}})}} \\ & 4{\text{H}}^{ + } + {\text{e}}^{ - } \to 2{\text{H}}_{{2({\rm {gas}})}} \\ \end{aligned} $$ (6) Due to

dependency of the reduction/oxidation (known as redox) potentials to the pH, these potentials were adopted at \(\hbox {pH}=0\), 7, and 12, similar to the previous studies73,74. In Fig. 11,

the HSE06 band edges of the \(\hbox {X}_2\hbox {YH}_2\) monolayers have been presented with respect to the vacuum level. As can be seen, at \(\hbox {pH}=0\), the \(\hbox {X}_2\hbox {PH}_2\)

and \(\hbox {X}_2\hbox {AsH}_2\) monolayers have suitable band edge for water splitting reaction while at \(\hbox {pH}=12\), all the monolayers are eligible. However, this reaction usually

occurs in a neutral environment (\(\hbox {pH}=7\)). At this pH, all the monolayers except \(\hbox {Ge}_2\hbox {BiH}_2\) satisfy the condition of the band edge position. As suggested by Zhang

et al, materials with indirect band gaps are more desirable for photocatalytic activity75, therefore \(\hbox {Si}_2\hbox {YH}_2\) monolayers will react better than \(\hbox {Ge}_2\hbox

{YH}_2\) ones. On the other hand, the band gap value should be smaller than 3 eV for enhancing the visible light absorption76,77, therefore the \(\hbox {Si}_2\hbox {PH}_2\) and \(\hbox

{Si}_2\hbox {AsH}_2\) monolayers, having large band gaps for visible light, cannot produce high efficiency for electron-hole generation and accordingly for water splitting. Summarily, the

\(\hbox {Si}_2\hbox {SbH}_2\) and \(\hbox {Si}_2\hbox {BiH}_2\) monolayers are very promising candidates for water splitting. CONCLUSION In summary, using first-principles calculations, for

the first time, we have proposed a new family of two-dimensional binary compounds with an empirical formula of \(\hbox {X}_2\hbox {Y}\), where X and Y belong to groups IV (Si and Ge) and V

(P, As, Sb, and Bi), respectively. Different from their pure structures, the hydrogenated (\(\hbox {X}_2\hbox {YH}_2\)) monolayers exhibit a very high stability according to cohesive energy,

phonon dispersion analysis, and AIMD simulations. We have obtained many interesting physical properties by computing the electrical, optical, and photocatalytic behavior of these

monolayers. Our calculations disclose that all of the monolayers are semiconductors with band gaps in the range of 1.57 to 3.19 eV. The optical results reveal that \(\hbox {Si}_2\hbox

{PH}_2\), \(\hbox {Si}_2\hbox {AsH}_2\), \(\hbox {Si}_2\hbox {SbH}_2\), and \(\hbox {Ge}_2\hbox {PH}_2\) monolayers have potential applications in beam splitting, and \(\hbox {Si}_2\hbox

{BiH}_2\), \(\hbox {Ge}_2\hbox {AsH}_2\), \(\hbox {Ge}_2\hbox {SbH}_2\), and \(\hbox {Ge}_2\hbox {BiH}_2\) monolayers are more favorable for energy harvesting systems and solar cells.

Besides, the \(\hbox {Si}_2\hbox {SbH}_2\) and \(\hbox {Si}_2\hbox {BiH}_2\) monolayers were found to have suitable band gaps and band edge positions for photocatalytic water splitting. Our

results suggest the binary monolayers of group IV-V for uses in nano-electronic and optoelectronic applications, and propose them for further experimental works. Finally, we predict that the

reported properties for \(\hbox {X}_2\hbox {YH}_2\) monolayers would be also similar to possible deposited \(\hbox {X}_2\hbox {Y}\) monolayers on a proper substrate such as Si (111), ZnS

(111), and SiC (111). REFERENCES * Novoselov, K. S. _et al._ Electric field effect in atomically thin carbon films. _Science_ 306, 666–669 (2004). ADS  CAS  PubMed  Google Scholar  * Hwang,

E. H. & Sarma, S. D. Acoustic phonon scattering limited carrier mobility in two-dimensional extrinsic graphene. _Phys. Rev. B_ 77, 115449 (2008). ADS  Google Scholar  * Frank, I. W.,

Tanenbaum, D. M., van der Zande, A. M. & McEuen, P. L. Mechanical properties of suspended graphene sheets. _J. Vac. Sci. Technol. B_ 25, 2558–2561 (2007). CAS  Google Scholar  * Nair, R.

R. _et al._ Fine structure constant defines visual transparency of graphene. _Science_ 320, 1308 (2008). ADS  CAS  PubMed  Google Scholar  * Lalmi, B. _et al._ Epitaxial growth of a

silicene sheet. _Appl. Phys. Lett._ 97, 223109 (2010). ADS  Google Scholar  * Li, L. _et al._ Buckled germanene formation on Pt (111). _Adv. Mater._ 26, 4820–4824 (2014). ADS  CAS  PubMed 

Google Scholar  * Ezawa, M. Monolayer topological insulators: silicene, germanene, and stanene. _J. Phys. Soc. Jpn._ 84, 121003 (2015). ADS  Google Scholar  * Acun, A. _et al._ Germanene:

the germanium analogue of graphene. _J. Phys. Condens. Matter_ 27, 443002 (2015). CAS  PubMed  Google Scholar  * Drummond, N. D., Zolyomi, V. & FalKo, V. I. Electrically tunable band gap

in silicene. _Phys. Rev. B_ 85, 075423 (2012). ADS  Google Scholar  * Liu, C.-C., Feng, W. & Yao, Y. Quantum spin hall effect in silicene and two-dimensional germanium. _Phys. Rev.

Lett._ 107, 076802 (2011). ADS  PubMed  Google Scholar  * Tabert, C. J. & Nicol, E. J. Valley-spin polarization in the magneto-optical response of silicene and other similar 2d crystals.

_Phys. Rev. Lett._ 110, 197402 (2013). ADS  CAS  PubMed  Google Scholar  * Zhang, S. _et al._ Semiconducting group 15 monolayers: a broad range of band gaps and high carrier mobilities.

_Angew. Chem. Int. Ed._ 55, 1666–1669 (2016). CAS  Google Scholar  * Kamal, C. & Ezawa, M. Arsenene: Two-dimensional buckled and puckered honeycomb arsenic systems. _Phys. Rev. B_ 91,

085423 (2015). ADS  Google Scholar  * Wang, G., Pandey, R. & Karna, S. P. Atomically thin group v elemental films: theoretical investigations of antimonene allotropes. _ACS Appl. Mater.

Interfaces_ 7, 11490–11496 (2015). CAS  PubMed  Google Scholar  * Aktürk, E., Aktürk, Oz. & Ciraci, S. Single and bilayer bismuthene: stability at high temperature and mechanical and

electronic properties. _Phys. Rev. B_ 94, 1–9 (2016). Google Scholar  * Pumera, M. & Sofer, Z. 2d monoelemental arsenene, antimonene, and bismuthene: Beyond black phosphorus. _Adv.

Mater._ 29, 1605299 (2017). Google Scholar  * Mozvashi, S. M., Vishkayi, S. I. & Tagani, M. B. Antimonene/bismuthene vertical van-der waals heterostructure: a computational study. _Phys.

E Low Dimens. Syst. Nanostruct._ 118, 113914 (2019). Google Scholar  * Bafekry, A., Mortazavi, B. & Shayesteh, S. F. Band gap and magnetism engineering in dirac half-metallic Na2C

nanosheet via layer thickness, strain and point defects. _J. Magn. Magn. Mater._ 491, (2019). * Hadipour, H. Screening of coulomb interaction and \(\pi \) magnetism in defected graphene.

_Phys. Rev. B_ 99, 1–11 (2019). Google Scholar  * Tagani, M. B. Electrical and mechanical properties of a fully hydrogenated two-dimensional polyaniline sheet. _Comput. Mater. Sci._ 153,

126–133 (2018). CAS  Google Scholar  * Shafique, A. & Shin, Y.-H. Thermoelectric and phonon transport properties of two-dimensional iv–vi compounds. _Sci. Rep._ 7, 506 (2017). ADS 

PubMed  PubMed Central  Google Scholar  * Mahmood, J. _et al._ Two-dimensional polyaniline (C3N) from carbonized organic single crystals in solid state. _Proc. Natl. Acad. Sci._ 113,

7414–7419 (2016). CAS  PubMed  Google Scholar  * Gou, J. _et al._ Binary two-dimensional honeycomb lattice with strong spin-orbit coupling and electron-hole asymmetry. _Phys. Rev. Lett._

121, 126801 (2018). ADS  CAS  PubMed  Google Scholar  * Barreteau, C., Michon, B., Besnard, C. & Giannini, E. High-pressure melt growth and transport properties of SiP, SiAs, GeP, and

GeAs 2d layered semiconductors. _J. Cryst. Growth_ 443, 75–80 (2016). ADS  CAS  Google Scholar  * Somaiya, R. N., Sonvane, Y. A. & Gupta, S. K. Exploration of the strain and

thermoelectric properties of hexagonal six (x= N, P, As, Sb, and Bi) monolayers. _Phys. Chem. Chem. Phys._ 22, 3990–3998 (2020). CAS  PubMed  Google Scholar  * Ma, Z., Zhuang, J., Zhang, X.

& Zhou, Z. Sip monolayers: New 2d structures of group iv–v compounds for visible-light photohydrolytic catalysts. _Front. Phys._ 13, 138104 (2018). ADS  Google Scholar  * Zhang, W., Yin,

J., Ding, Y., Jiang, Y. & Zhang, P. Strain-engineering tunable electron mobility of monolayer iv–v group compounds. _Nanoscale_ 10, 16750–16758 (2018). CAS  PubMed  Google Scholar  *

Zhang, W. & Xiao, Y. Mechanism of electrocatalytically active precious metal (Ni, Pd, Pt, and Ru) complexes in the graphene basal plane for ORR applications in novel fuel cells. _Energy

Fuels_ 34, 2425–2434 (2020). CAS  Google Scholar  * Mielke, A. Ferromagnetism in single-band Hubbard models with a partially flat band. _Phys. Rev. Lett._ 82, 4312 (1999). ADS  CAS  Google

Scholar  * Shen, Z. X. & Dessau, D. S. Electronic structure and photoemission studies of late transition-metal oxides–mott insulators and high-temperature superconductors. _Phys. Rep._

253, 1–162 (1995). ADS  Google Scholar  * Boustani, I. New quasi-planar surfaces of bare boron. _Surf. Sci._ 370, 355–363 (1997). ADS  CAS  Google Scholar  * Giannozzi, P. . _et al._ Quantum

espresso: a modular and open-source software project for quantum simulations of materials. _J. Phys. Condens. Matter_ 21, 395502 (2009). PubMed  Google Scholar  * Perdew, J. P., Burke, K.

& Ernzerhof, M. Generalized gradient approximation made simple. _Phys. Rev. Lett._ 77, 3865 (1996). ADS  CAS  Google Scholar  * Ding, Y. & Wang, Y. Stabilizing the isolated Sn2Bi

nanosheet and tailoring its electronic structure by chemical functionalization: a computational study. _Appl. Phys. Lett._ 114, 073103 (2019). ADS  Google Scholar  * Mohebpour, M. A.,

Vishkayi, S. I. & Tagani, M. B. Tuning electronic and optical properties of free-standing Sn2Bi monolayer stabilized by hydrogenation. _J. Appl. Phys._ 127, 014302 (2020). ADS  CAS 

Google Scholar  * Elias, D. C. _et al._ Control of graphenes properties by reversible hydrogenation: evidence for graphane. _Science_ 323, 610–613 (2009). ADS  CAS  PubMed  Google Scholar  *

Sofo, J. O., Chaudhari, A. S. & Barber, G. D. Graphane: a two-dimensional hydrocarbon. _Phys. Rev. B_ 75, 153401 (2007). ADS  Google Scholar  * Pumera, M. & Wong, C. H. A. Graphane

and hydrogenated graphene. _Chem. Soc. Rev._ 42, 5987–5995 (2013). CAS  PubMed  Google Scholar  * Hou, C., Tai, G., Hao, J., Sheng, L., Liu, B. & Wu, Z. Ultrastable crystalline

semiconducting hydrogenated borophene. _Angew. Chemie_ 132(27), 10911–10917. https://doi.org/10.1002/ange.202001045 (2020). * Xu, L.-C., Du, A. & Kou, L. Hydrogenated borophene as a

stable two-dimensional dirac material with an ultrahigh fermi velocity. _Phys. Chem. Chem. Phys._ 18, 27284–27289 (2016). CAS  PubMed  Google Scholar  * Li, X. _et al._ Tuning the electronic

and mechanical properties of penta-graphene via hydrogenation and fluorination. _Phys. Chem. Chem. Phys._ 18, 14191–14197 (2016). CAS  PubMed  Google Scholar  * Goli, M., Ansari, R., Rouhi,

S., Aghdasi, P. & Mozvashi, S. Influence of f and h adsorption on the elasto-plastic properties of silicene: A dft investigation. _Phys. E Low Dimens. Syst. Nanostruct._ 119, 113984

(2020). CAS  Google Scholar  * Trivedi, S., Srivastava, A. & Kurchania, R. Silicene and germanene: a first principle study of electronic structure and effect of

hydrogenation-passivation. _J. Comput. Theor. Nanos_ 11, 781–788 (2014). CAS  Google Scholar  * Chen, X. _et al._ The electronic and optical properties of novel germanene and antimonene

heterostructures. _J. Mater. Chem. C_ 4, 5434–5441 (2016). CAS  Google Scholar  * Yu, W., Niu, C.-Y., Zhu, Z., Wang, X. & Zhang, W.-B. Atomically thin binary v–v compound semiconductor:

a first-principles study. _J. Mater. Chem. C_ 4, 6581–6587 (2016). CAS  Google Scholar  * Zheng, H. _et al._ Monolayer ii–vi semiconductors: a first-principles prediction. _Phys. Rev. B_ 92,

115307 (2015). ADS  Google Scholar  * Guo, S.-D. & Liu, J.-T. Lower lattice thermal conductivity in SbAs than as or Sb monolayers: a first-principles study. _Phys. Chem. Chem. Phys_ 19,

31982–31988 (2017). CAS  PubMed  Google Scholar  * Wang, S., Wang, W. & Zhao, G. Thermal transport properties of antimonene: an ab initio study. _Phys. Chem. Chem. Phys._ 18,

31217–31222 (2016). CAS  PubMed  Google Scholar  * Kumar, S., Sharma, S., Babar, V. & Schwingenschlögl, U. Ultralow lattice thermal conductivity in monolayer C 3 N as compared to

graphene. _J. Mater. Chem. A_ 5, 20407–20411 (2017). CAS  Google Scholar  * Kocabaş, T. _et al._ A distinct correlation between the vibrational and thermal transport properties of group va

monolayer crystals. _Nanoscale_ 10, 7803–7812 (2018). PubMed  Google Scholar  * Nika, D. . L. . & Balandin, A. . A. . Two-dimensional phonon transport in graphene. _J. Phys. Condens.

Matter_ 24, 233203 (2012). ADS  PubMed  Google Scholar  * Özdamar, B. _et al._ Structural, vibrational, and electronic properties of single-layer hexagonal crystals of group iv and v

elements. _Phys. Rev. B_ 98, 045431 (2018). ADS  Google Scholar  * Mogulkoc, A., Mogulkoc, Y., Jahangirov, S. & Durgun, E. Characterization and stability of janus TIXY (x/y= S, Se, and

Te) monolayers. _J. Phys. Chem. C_ 123, 29922–29931 (2019). CAS  Google Scholar  * Kittel, C., McEuen, P. & McEuen, P. _Introduction to Solid State Physics_ Vol. 8 (Wiley, New York,

1996). Google Scholar  * Pekoz, R., Konuk, M., Kilic, M. E. & Durgun, E. Two-dimensional fluorinated boron sheets: mechanical, electronic, and thermal properties. _ACS Omega_ 3,

1815–1822 (2018). CAS  PubMed  PubMed Central  Google Scholar  * Lysogorskiy, Y. V., Eremina, R. M., Gavrilova, T. P., Nedopekin, O. V. & Tayurskii, D. A. Vibrational and magnetic

properties of crystalline cute 2 o 5. _JETP Lett._ 100, 652–656 (2015). ADS  CAS  Google Scholar  * Zhang, H. & Chen, M. Two-dimensional \(\beta \)-phase group-VA binary compounds for

versatile electronic and optical properties. _J. Mater. Chem. C_ 6, 11694–11700 (2018). CAS  Google Scholar  * Zhang, D.-C., Zhang, A.-X., Guo, S.-D. & Duan, Y.-F. Thermoelectric

properties of \(\beta \)-As, Sb and Bi monolayers. _RSC Adv._ 7, 24537–24546 (2017). Google Scholar  * Guo, S.-D. Biaxial strain tuned thermoelectric properties in monolayer PtSe 2. _J.

Mater. Chem. C_ 4, 9366–9374 (2016). CAS  Google Scholar  * Aktürk, Oz., Özçelik, V. O. & Ciraci, S. Single-layer crystalline phases of antimony: Antimonenes. _Phys. Rev. B_ 91, 235446

(2015). ADS  Google Scholar  * Cahangirov, S., Topsakal, M., Aktürk, E., Şahin, H. & Ciraci, S. Two-and one-dimensional honeycomb structures of silicon and germanium. _Phys. Rev. Lett._

102, 236804 (2009). ADS  CAS  PubMed  Google Scholar  * Li, Z. _et al._ Electronic properties of two-dimensional iv–v group materials from density functional theory. _Appl. Surf. Sci._ 496,

143730 (2019). CAS  Google Scholar  * Wang, H. _et al._ First-principles study of electronic, optical and thermal transport properties of group iii–vi monolayer mx (m= ga, in; x= s, se). _J.

Appl. Phys._ 125, 245104 (2019). ADS  Google Scholar  * Xu, Y. _et al._ First-principle calculations of optical properties of monolayer arsenene and antimonene allotropes. _Ann. Phys._ 529,

1600152 (2017). MathSciNet  Google Scholar  * Gajdoš, M., Hummer, K., Kresse, G., Furthmüller, J. & Bechstedt, F. Linear optical properties in the projector-augmented wave methodology.

_Phys. Rev. B_ 73, 045112 (2006). ADS  Google Scholar  * Benassi, A. Pwscf’s epsilon. x user’s manual. Report, Technical Report, Physics Department, Universita degli Studi di Modena e. . .

(2008). * Carcione, J. M., Cavallini, F., Ba, J., Cheng, W. & Qadrouh, A. N. On the Kramers–Kronig relations. _Rheol. Acta_ 58, 21–28 (2019). CAS  Google Scholar  * Singh, D., Gupta, S.

K., Sonvane, Y. & Lukačević, I. Antimonene: a monolayer material for ultraviolet optical nanodevices. _J. Mater. Chem. C_ 4, 6386–6390 (2016). CAS  Google Scholar  * Mohan, B., Kumar, A.

& Ahluwalia, P. K. Electronic and optical properties of silicene under uni-axial and bi-axial mechanical strains: a first principle study. _Phys. E Low Dimens. Syst. Nanostruct._ 61,

40–47 (2014). ADS  CAS  Google Scholar  * Chen, X. _et al._ Recent advances in visible-light-driven photoelectrochemical water splitting: catalyst nanostructures and reaction systems.

_Nano-Micro Lett._ 8, 1–12 (2016). Google Scholar  * Jeong, S. Y., Song, J. & Lee, S. Photoelectrochemical device designs toward practical solar water splitting: A review on the recent

progress of bivo4 and bifeo3 photoanodes. _Appl. Sci._ 8, 1388 (2018). Google Scholar  * Zhu, Y.-L. _et al._ Two-dimensional silicon chalcogenides with high carrier mobility for

photocatalytic water splitting. _J. Mater. Sci._ 54, 11485–11496 (2019). ADS  CAS  Google Scholar  * Chowdhury, C., Karmakar, S. & Datta, A. Monolayer group iv–vi monochalcogenides:

low-dimensional materials for photocatalytic water splitting. _J. Phys. Chem. C_ 121, 7615–7624 (2017). Google Scholar  * Zhang, X. _et al._ Computational screening of 2d materials and

rational design of heterojunctions for water splitting photocatalysts. _Small Methods_ 2, 1700359 (2018). Google Scholar  * Zhang, P., Zhang, J. & Gong, J. Tantalum-based semiconductors

for solar water splitting. _Chem. Soc. Rev._ 43, 4395–4422 (2014). CAS  PubMed  Google Scholar  * Yang, H. _et al._ A theoretical study on the electronic properties of in-plane cds/znse

heterostructures: type-ii band alignment for water splitting. _J. Mater. Chem. A_ 6, 4161–4166 (2018). CAS  Google Scholar  * Liao, P. & Carter, E. A. New concepts and modeling

strategies to design and evaluate photo-electro-catalysts based on transition metal oxides. _Chem. Soc. Rev._ 42, 2401–2422 (2013). CAS  PubMed  Google Scholar  Download references

ACKNOWLEDGEMENTS We are thankful to the Research Council of University of Guilan for the partial support of this research. AUTHOR INFORMATION Author notes * These authors contributed

equally: Mohammad Ali Mohebpour and Shobair Mohammadi Mozvashi. AUTHORS AND AFFILIATIONS * Computational Nanophysics Laboratory (CNL), Department of Physics, University of Guilan, P. O. Box

41335-1914, Rasht, Iran Mohammad Ali Mohebpour, Shobair Mohammadi Mozvashi & Meysam Bagheri Tagani * School of Physics, Institute for Research in Fundamental Sciences (IPM), P. O. Box

19395-5531, Tehran, Iran Sahar Izadi Vishkayi Authors * Mohammad Ali Mohebpour View author publications You can also search for this author inPubMed Google Scholar * Shobair Mohammadi

Mozvashi View author publications You can also search for this author inPubMed Google Scholar * Sahar Izadi Vishkayi View author publications You can also search for this author inPubMed 

Google Scholar * Meysam Bagheri Tagani View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS M.A.M. and S.M.M. performed the DFT based

simulations. M B.T. and S.I.V. conceived the study. M.A.M. and S.M.M. wrote the initial draft and all authors reviewed the manuscript. CORRESPONDING AUTHOR Correspondence to Meysam Bagheri

Tagani. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE Springer Nature remains neutral with regard to

jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY MATERIAL 1 RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a

Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit

to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are

included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons

licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of

this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Mohebpour, M.A., Mozvashi, S.M., Vishkayi, S.I. _et al._

Prediction of hydrogenated group IV–V hexagonal binary monolayers. _Sci Rep_ 10, 14963 (2020). https://doi.org/10.1038/s41598-020-71766-5 Download citation * Received: 06 July 2020 *

Accepted: 18 August 2020 * Published: 11 September 2020 * DOI: https://doi.org/10.1038/s41598-020-71766-5 SHARE THIS ARTICLE Anyone you share the following link with will be able to read

this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative