Revisiting goodenough-kanamori rules in a new series of double perovskites lasr1−xcaxnireo6

ABSTRACT The magnetic ground states in highly ordered double perovskites LaSr1−_x_Ca_x_NiReO6 (_x_ = 0.0, 0.5, 1.0) are studied in view of the Goodenough-Kanamori rules of superexchange

interactions in this paper. In LaSrNiReO6, Ni and Re sublattices are found to exhibit curious magnetic states separately, but no long range magnetic ordering is achieved. The magnetic

transition at ~255 K is identified with the independent Re sublattice magnetic ordering. Interestingly, the sublattice interactions are tuned by modifying the Ni-O-Re bond angles through Ca

doping. Upon Ca doping, the Ni and Re sublattices start to display a ferrimagnetically ordered state at low temperature. The neutron powder diffraction data reveals long range ferrimagnetic

ordering of the Ni and Re magnetic sublattices along the crystallographic _b-_axis. The transition temperature of the ferrimagnetic phase increases monotonically with increasing Ca

concentration. SIMILAR CONTENT BEING VIEWED BY OTHERS BEHAVIOR OF MAGNETOELECTRIC HYSTERESIS AND ROLE OF RARE EARTH IONS IN MULTIFERROICITY IN DOUBLE PEROVSKITE YB2COMNO6 Article Open access

10 December 2021 CUBIC DOUBLE PEROVSKITES HOST NONCOPLANAR SPIN TEXTURES Article Open access 06 June 2024 MIXED ORBITAL STATES AND MODULATED CRYSTAL STRUCTURES IN LA1−_X_CA_X_MNO3 DEDUCED

FROM SYNCHROTRON X-RAY DIFFRACTION Article Open access 26 July 2023 INTRODUCTION Double perovskites (DP; _A_2_BB_′ O6)1,2,3 belong to a class of materials which exhibit many interesting

properties and rich physics. Understandably, the choice of the transition metal ions at the _B_ and _B_′ sites with different electron occupancies decide the material properties of the DPs.

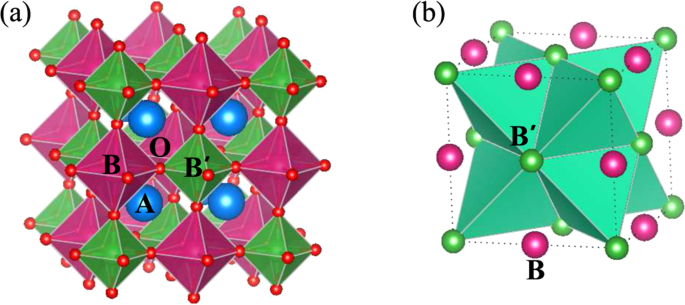
When both _B_ and _B_′ are magnetic ions, the magnetic and electronic properties of the system are governed by _B_-O-_B_′ interaction within a rock salt type structural definition as shown

in Fig. 1(a). For example, the high temperature ferromagnetic (FM) order (_T__C_ > 400 K) of the DP compounds, Sr2FeMoO6 and Sr2FeReO6 is explained by a generalized double exchange

mechanism through electronic band filling of the (Mo/Re) _t_2_g_↓-O-Fe _t_2_g_↓ conduction band4. However, if the _B_-site ion is non-magnetic, the magnetic ground state would be defined by

the edge-shared network of tetrahedra comprising the _B_′ magnetic ions (Fig. 1(b)). Such systems often exhibit geometric frustration in presence of antiferromagnetic nearest-neighbor

correlations. Recently, detailed theoretical investigations have been carried out on similar DPs with the magnetic _B_′ ions, having _nd_1 and _nd_2 (_n_ = 4, 5) electronic configurations

and significant spin orbit coupling (SOC)5,6. Here, the nearest neighbor distance between the tetrahedrally arranged 4_d_/5_d_ magnetic ions naturally becomes much larger compared to the

cases when both _B_ and _B_′ sites are filled up with the magnetic ions. This reduces the inter-atomic exchange between the magnetic ions which helps to protect the SOC driven states. This

situation opens up many options, and consequently many double perovskites with _d_1 (e.g., Ba2YMoO6, Sr2CaReO6, Sr2MgReO6, Ba2NaOsO6 etc.) as well as _d_2 electronic configurations (e.g.,

Ba2CaOsO6, Ba2YReO6, La2LiReO6 etc.) have been studied, where numerous unusual magnetic ground states are revealed7,8,9,10,11,12,13,14,15. Another interesting possibility appears in DPs,

when both _B_ and _B_′ ions are magnetic, but the valence electrons of _B_ ion lack the orbital symmetry of the same of _B_′ ion for effective _B_-O-_B_′ super-exchange interaction. Such a

situation will give rise to two noninteracting or weakly interacting magnetic sublattices. It will be interesting to gradually manipulate the extent of _B_-O-_B_′ interaction by carefully

changing the _B_-O-_B_′ angle, and consequently follow the evolution of two sublattices getting engaged in single magnetic lattice (Fig. 1(b) → Fig. 1(a)), following the famous

Goodenough-Kanamori rule. Accordingly, we have designed a series of DPs, LaSr1−_x_Ca_x_NiReO6, having a combination of 3_d_ and 5_d_ transition metals Ni2+ (3_d_8, _t_2_g_6_e__g_2) and Re5+

(5_d_2, _t_2_g_2) at the _B_ and _B_′ sites, respectively. Due to large crystal field splitting, the empty _e__g_ orbitals of Re have much higher energy than the _t_2_g_ manifold and do not

contribute in any interatomic exchange interaction. The filled _t_2_g_ orbital of Ni as well has less involvement in the exchange interaction. The only possible exchange interaction that can

be active between the _e__g_ of Ni2+ and the _t_2_g_ of Re5+, will be very weak if the _B_-O-_B_′ angle is strictly 180°, as the overlap integral between the _e__g_ and the _t_2_g_ becomes

zero. However, finite overlap between these orbitals can be introduced by tuning the bond angles and lattice parameters as a consequence of the doping of Sr2+ ions by smaller sized Ca2+

ions. In our design criteria of the ordered LaSr1−_x_Ca_x_NiReO6 series, _B_, _B_′ cations are also selected in such a way that there are large differences in their charge and ionic radii,

in order to achieve complete _B_, _B_′ rock-salt ordering. Here the ionic radii of Ni2+ (=0.69 Å) and Re5+ (=0.58 Å)16 do fulfill the above criteria. Detailed magnetic measurements on

LaSr1−_x_Ca_x_NiReO6 indicate curious evolution of magnetic states as a function of doping. For LaSrNiReO6, the system undergoes multiple magnetic transitions, indicated by a divergence

between ZFC and FC at ~255 K, typical of Re5+ _t_2_g_2 ions confined in a fcc sublattice, and by a down turn in magnetization at ~27 K, observed in both the ZFC and FC curves. Transport

measurements confirm purely insulating behavior of the samples. However with Ca doping, the structure undergoes into larger monoclinic distortion, which results in a larger deviation of the

Ni-O-Re (∠NOR) bond angles from 180°. This deviation enables substantial superexchange interaction between the Ni _e__g_ and Re _t_2_g_ orbitals, resulting to an overall ferrimagnetic order

between two individual ferromagnetic sublattices. RESULTS All the samples appeared to be single phased as no impurity peak is detected in the whole 2_θ_ range in the powder XRD data,

collected at room temperature for LaSr1−_x_Ca_x_NiReO6 (LSCNRO) series (see Fig. 2(a,b)). The observed (circle), calculated (line through the data) and the difference (blue dashed line)

diffraction data are shown in Fig. 2 for _x_ = 0.0 and 1.0 compositions respectively, which could be fitted with the _P_21/_n_ space group. The system shows increase in monoclinic distortion

(see the insets to Fig. 2(a,b)) with increasing Ca concentration (see Fig. S1 in SI to compare the XRD patterns for all the three compositions collected at a synchrotron X-ray source). The

observation of the monoclinic distortion in this series of compounds is in agreement with the calculated tolerance factors (_f_), which goes from _f_ = 0.98 (_x_ = 0.0) to _f_ = 0.96 (_x_ = 

1.0). An overall shift of the Bragg peaks towards higher 2_θ_ indicates a decrease of the unit cell parameters with increasing _x_. Presence of the intense peak at around 19.6° (1 1 0)

indicates high degree of Ni/Re ordering within the double perovskite structure of LaSr1−_x_Ca_x_NiReO6 for _x_ = 0.0 and 1.0 compositions. A combined refinement of XRD and NPD patterns was

carried out for both the compositions at 300 K in order to accurately quantify Ni and Re cation ordering and determine the oxygen positions. The refined structural parameters along with the

bond lengths and bond angles are given in Tables 1 and 2 respectively. The ordering between Ni and Re is quantified to be 96% and 99% for _x_ = 0.0 and _x_ = 1.0 from the refined occupation

numbers of Ni1/Re1 and Re2/Ni2 at (0.5, 0.0, 0.5) and (0.5, 0.0, 0.0) crystallographic sites, respectively. The stoichiometry of Ni and Re in the compounds are probed and confirmed through

ICP-OES experiments (see SI). The Bond Valence Sum (BVS) for Ni is calculated from the Ni-O bond lengths listed in Table 217. The values obtained are 2.2 for both the composition which is in

accordance with the expected oxidation state of the Ni ions in these compounds. Next, we have performed X-ray absorption spectroscopy (XAS) at the _L_-edge of Ni to further verify the

charge state. The XAS spectra collected for _x_ = 0.0, 0.5, 1.0 compositions are shown in Fig. 3, together with the reference spectra for Ni2+ and Ni3+. The reference spectra are obtained by

digitizing and recalling the data points from the Figs. 4 and 6(a) of the ref. 18. Note that the La _M_3/2 absorption edge is superimposed with the Ni _L_3/2-edge. The spectral features of

both the Ni _L_3/2 and _L_1/2 are quite different for Ni2+ and Ni3+. Both _L_3/2 and _L_1/2 consist of two peaks indicated by the arrows in the figure. In the 2+ charge state of Ni as in

NiO, the lower energy peak of _L_3/2 is much more intense relative to the higher energy one, while both the peaks have similar intensities in case of NdNiO3, PrNiO3 and LaNiO3, containing

Ni3+ ions18. Also, the spectral feature of the _L_1/2 edge of all the three compositions, clearly resemble to that of NiO. Hence it can be inferred that Ni is in 2+ charge state for all the

LSCNRO compositions. In order to maintain charge neutrality, the charge state of Re should then be 5+ as Sr2+, La3+ and O2− are expected to be very stable at their respective ionic states.

The electrical resistivity (_ρ_) of the two end member compounds as a function of temperature are shown in Fig. 4. The resistivity data were fitted using an activated transport model as well

as using variable range hopping model. Both the data were nonlinear on a _T_−1 scale and was found to be linear on a _T_−1/4 scale (see inset to Fig. 4(a,b)), in accordance with a

three-dimensional variable range hopping transport model19. The insulating nature of the compounds can be explained by the fact that Ni2+; 3_d_8 effectively provides electrons of _e__g_

symmetry at the valence band as the _t_2_g_ bands are completely filled up, while Re5+; 5_d_2 has partially filled _t_2_g_ bands, thus from the symmetry consideration the electron hopping is

prohibited (see the inset of Fig. 4(a)). However, a nonzero hopping probability is realized if the bond angles deviate sufficiently from 180°, thereby enabling Ni_e__g_-Re _t_2_g_

hybridization via oxygen (compare the inset to Fig. 4(b)). Replacing Sr2+ by the smaller Ca2+ ion, we anticipate a larger octahedral distortion that can provide a route for hybridization

between the Ni_e__g_ and Re _t_2_g_. Indeed a larger amount of distortion is achieved as understood from the crystal structure of LaCaNiReO6 and consequently a clear decrease in the

resistivity is also observed, although the temperature dependence still suggests that the material is best described as an insulator/semiconductor. Next, we have looked into the magnetic

properties in details. The zero field cooled (ZFC) and field cooled (FC) data recorded with an applied field of 200 Oe for the three compositions of LSCNRO are shown in Fig. 5(a–c). The

_M_(_T_) of _x_ = 0.0 sample shows a transition at around 255 K where ZFC and FC curves start to bifurcate. Another transition occurs at around 27 K, where susceptibility seems to saturate.

In the high temperature regime (255–300 K), the inverse susceptibility follows the Curie-Weiss behavior resulting (see Fig. S2(a)) in a effective moment of _μ__eff_ = 3.07 _μ__B_. The

observed magnetic moment is lower than the expected spin-only contribution of both Ni2+ and Re5+ and this reduction in magnitude can attributed to the spin-orbit coupling in Re4,20. For _x_ 

= 0.5 (Fig. 5(b)) a ferro/ferrimagnetic (FM) like transition is observed at 45 K, along with the high temperature FC-ZFC bifurcated curves. This FM like transition gradually shifts to higher

temperatures with increasing _x_ (~110 K for _x_ = 1.0; Fig. 5(c)). Also as _x_ increases, the FM like transition becomes stronger to obscure the high temperature FC-ZFC splitting. The

effective magnetic moment obtained from Curie-Weiss fit for _x_ = 1.0 (see Fig. S2(b)) is 3.59 _μ__B_. The magnetization versus field (_M_(_H_)) data, collected at 5 K for the three

compositions are plotted in Fig. 5(d). The coercivity of all the samples are very high in general, which arises as a result of large spin-orbit coupling driven anisotropy, commonly observed

for Re based DPs4,20. However, the overall nature of the _M_(_H_) curves varies drastically with _x_. The remnant magnetization increases continuously with clear signatures of magnetic

saturation as a function of Ca-doping. This observation clearly suggests significant changes in magnetic interactions with increasing monoclinic distortions and decreasing _B_-O-_B_′ angle.

In order to have more insight about the observed magnetic transitions, neutron powder diffraction (NPD) were carried out for the end compositions at 2 K. The changes in the lattice

parameters, bond lengths and bond angles with temperature have been listed in Tables 1 and 2. For _x_ = 0.0, there is a contraction of the lattice parameters with decrease in temperature

with no signature of long range magnetic ordering (see Fig. 6(a)), which suggests that the observed magnetic transitions in the magnetization curves are of short range type. Our observation

is in accordance with the NPD measurements of SrLaNiReO6 reported in ref. 21 which also lacked evidence of long-range magnetic ordering. The neutron diffraction patterns of _x_ = 1.0

recorded at 2 K and 300 K are shown in Fig. 7(a). From, Table 1 it is evident that there is a elongation in the lattice parameter along _b_ axis with the decrease in temperature. Contrary to

_x_ = 0.0, it is observed that the nuclear peak profile in the vicinity of 24° comprising(011), (101), and (−101) nuclear Bragg peaks clearly gets enhanced in intensity at 2 K. Since no

extra magnetic reflections with significant intensity are observed, the magnetic structure can be assumed to coincide with the crystal structure and propagation vector _K_ = (000) may be

used to model the structure. Thus, using the formalism of propagation vectors in conjunction with the irreducible representation analysis as described in ref. 22, the magnetic reducible

representation for the magnetic atoms can be decomposed as a direct sum of irreducible representations. For the refinement of the magnetic structure, the symmetry elements and basis vectors

of the irreducible representations (Γ) for magnetic Ni (Re) atom were obtained using _BasIre_p_s_ program available within the FullProf suite, using the propagation vector _K_ = (000). It is

observed that the magnetic representation of Ni (Re) ion comprises two irreducible representations Γ = Γ1 + Γ3. The two Γ values were tested sequentially with the measured pattern at 2 K

and we could refine the magnetic structure satisfactorily using the basis vectors of Γ1. Although using this same representation, a collection of peaks at around 2_θ_ = 47° shows magnetic

contributions, the magnetic structure factor turns out to be less than 1% of the nuclear intensity with magnetic form factor for Ni2+ being around 0.7 at this Q-value, which hinders the

accurate estimation of the magnetic structure from this peak. Thus the most probable magnetic structure can be estimated from the peak near 24° using the basis vectors of Γ1. It was found

that the Ni (Re) moments lie predominantly along negative (positive) _b_ direction with a very small canting, which could not be resolved within the measuring capability. Hence, the moments

were constrained along _b_ direction and refined. The obtained moments on Ni and Re are −2.0 (4) _μ__B_ and 1.0 (4) _μ__B_ (Table 3, Fig. 8), respectively, resulting in a net magnetic moment

of ~1.0 _μ__B_ per formula unit along the negative _b_ direction. DISCUSSIONS In a highly ordered _B_-site double perovskite with magnetic ions at _B_ and _B_′ sites the long range magnetic

order is always determined by the type of active exchange interaction that mediates through the _B_-O-_B_′ connectivity. For localized electrons (i.e. the _d_ electrons), the magnetic

interaction between two transition metal _B_ and _B_′ cations is often described by the Goodenough-Kanamori rules of superexchange interaction23,24. According to this rule, when the orbitals

of two magnetic ions have a significant overlap integral, the superexchange is antiferromagnetic (∠_e__g_(_B_)-O-_e__g_(_B_′) = 180°, ∠_t_2_g_(_B_)-O-_t_2_g_(_B_′) = 180°,

∠_t_2_g_(_B_)-O-_e__g_(_B_′) = 90°). However, when the orbitals are arranged in such a way that they are expected to be in contact but to have no/weak overlap integral - most notably _t_2_g_

and _e__g_ in 180° position, where the overlap is zero by symmetry, the rules predict ferromagnetic interaction, which is usually very weak in strength. In case of highly ordered

LaSr1−_x_Ca_x_NiReO6 compounds, Ni 3_d_ and Re 5_d_ orbitals are connected via oxygen 2 _p_ orbitals. From refinement of XRD and NPD, the average Ni-O-Re bond angle (∠NOR) comes about 160°

for _x_ = 0.0 sample and ~152° for _x_ = 1.0 sample. Therefore in case of _x_ = 0.0 sample, when ∠NOR is closer to 180°, the superexchange interaction between half filled _e__g_ orbitals of

Ni2+ and partially filled _t_2_g_ orbitals of Re5+ is a weak ferromagnetic interaction. Of course, there could be magnetic signals appearing from independent Ni and Re sublattices as well.

However, as the ∠NOR start deviating noticeably from 180° (e.g. _x_ = 1.0), a sizeable overlap between the _e__g_ and _t_2_g_ orbitals starts to favor antiferromagnetic (AFM) interaction

between the partially filled Ni _e__g_ and Re _t_2_g_ orbitals following the Goodenough-Kanamori rule. Further, we have noticed that the smaller volume of the _x_ = 1.0 sample compared to

_x_ = 0.0 sample has no significant effect in the Ni/Re-O bond lengths. The reduction of the lattice parameters are compensated by the smaller ∠NOR angles. We conclude that the low

temperature magnetic feature observed in _x_ = 0.0 compound could very well be a reminiscence of the weak ferromagnetism predicted by Goodenough-Kanamori rule, but could also be an

independent Ni sublattice feature as is seen in other Ni analog samples, such as, Sr2NiWO6 and Sr2NiTeO6 with nonmagnetic W6+ ([_Xe_] 4_f_ 14) and Te6+ ([_Kr_] 4_d_10) at the _B_′ site,

where the antiferromagnetic transition occurs at 35 K and 54 K, respectively25. This low temperature transition has been identified as the onset of a spin glass behavior in _x_ = 0.0

compound21. On the other hand, the observed bifurcation between ZFC and FC curves at higher temperatures in _x_ = 0.0 compound is clearly very similar to what is commonly observed when

Re-ion sits in the geometrically frustrated fcc lattice (the _B_′-site) within the double perovskite structure, but having nonmagnetic _B_-site ions, e.g., Sr2CaReO610, Sr2InReO626. For _x_ 

= 1.0 sample, further deviation of ∠NOR from 180° compared to that of _x_ = 0.0 enables an antiferromagnetic interaction between Ni2+ and Re5+ ions. In an ordered structure, this will result

the moment of the individual sublattice to order along the same direction. Strong spin-orbit interaction may result magneto-crystalline anisotropy in case of the Re 5_d_ spins, while the Ni

spins, residing in more isotropic 3_d_ orbitals, will orient antiparallel to Re spins following the super-exchange interaction. Therefore, the final magnetic structure is resulted in an

ferrimagnetic arrangement between the two sublattices along the crystallographic _b_-axis. In LSCNRO, both Ni2+ and Re5+ ions have two unpaired electrons. However, the strong spin-orbit

coupling in 5_d_ orbitals (relative to 3_d_ orbitals) usually results in a reduced total moment in Re ions compared to its spin only value27,28,29, which is clearly observed from the NPD

analysis. The net magnetic moment of ~1.0 _μ__B_ /f.u. obtained from NPD is in good agreement with the observed moment in _M_ vs _H_ data at the highest applied field ~0.75 _μ__B_ /f.u.). In

conclusion, a series of double perovskites, LaSr1−_x_Ca_x_NiReO6 (_x_ = 0.0, 0.5, 1.0) is realized with partially filled orbitals of _e__g_ and _t_2_g_ symmetries (local) at highly ordered

_B_ and _B_′-sites respectively. All the compositions adopt a monoclinic structure. In LaSrNiReO6 (_x_ = 0.0), an unusual divergence between the ZFC and FC curves is identified with the

magnetic state that arises from Re _t_2_g_2 ions sitting in a geometrically frustrated fcc sublattice in DP host. At low temperature (~27 K), the system undergoes another magnetic

transition, where weak ferromagnetism predicted by Goodenough-Kanamori rule could be identified. As lattice parameter decreases with Ca doping, the reduced Ni-O-Re bond angle introduces

nonzero overlap integral between Ni _e__g_ and Re _t_2_g_ orbitals, which favors a ferrimagnetic alignment between Ni and Re sublattices along the _b_-axis. The neutron powder diffraction

measurement conducted at room temperature and low temperature (2 K) revealed that the _x_ = 0.0 sample possesses a disordered/short-range magnetic state at low temperature, while for Ca

sample, the Ni and Re sublattices aligned ferrimagnetically to give a long range magnetic order evidenced from the magnetic Bragg peak corresponding to the double perovskite superlattice

peak. METHODS Four samples of LaSr1−_x_Ca_x_NiReO6 (LSCNRO) (_x_ = 0.0, 0.5, 1.0) were synthesized by solid state synthesis route. Highly pure La2O3, SrCO3, CaCO3, NiO, Re2O7 and Re metal

were used as the starting materials. The synthesis was done in two steps. In the first step, La2NiO4 was made by heating a mixture of stoichiometric La2O3 and NiO at 1250 °C in an inert

atmosphere for 48 hours with several intermediate grinding. SrO and CaO were used after heating them at 1250 °C and 1000 °C for 12 hours in an inert atmosphere. Next, stoichiometric amount

of La2NiO4, SrO, CaO, NiO, Re2O7 and Re metal were mixed inside a glovebox and the resultant mixture was sealed inside a quartz tube, which was then annealed at 1200 °C for the final

product. The phase purity of the three samples (_x_ = 0.0, 0.5, 1.0) were checked by x-ray diffraction (XRD) Bruker AXS: D8 Advance x-ray diffractometer (Cu _K__α_; _λ__α_ = 1.54059 Å) as

well as at MCX beamline of the Elettra Synchrotron Centre, Italy using wavelength of 0.751 Å. The XRD data were analyzed via Rietveld refinement using the FullProf 30 program. La, Ca, Sr,

Ni, Re quantitative analysis were performed in Inductively Coupled Plasma Optical Emission Spectroscopy (ICP-OES) (Perkin-Elmer USA, Optima 2100 DV) instrument following standard protocol of

sample analysis. _d_._c_. magnetic measurements were carried out in a Quantum Design SQUID magnetometer. Resistivity measurements were performed in a home made four probe setup. Soft x-ray

absorption spectroscopy (XAS) was performed at I1011 beamlines of the Swedish synchrotron facility MAX-lab, Lund. All the XAS spectra were measured by recording the total electron yield.

Neutron powder diffraction (NPD) measurements were performed using the HRPT31 diffractometer at the Paul Scherrer Institut, SINQ (Switzerland). The neutron wavelength was set to _λ_ = 1.89 Å

and about 1 g of _x_ = 0.0 and _x_ = 1.0 samples were used. Magnetic structure refinements were performed using the FullProf suite30. REFERENCES * Anderson, M. T., Greenwood, K. B., Taylor,

G. A. & Poeppelmeier, K. R. B-cation arrangements in double perovskites. _Prog. Solid State Chem._ 22, 197–233 (1993). Article  CAS  Google Scholar  * Knapp, M. C. & Woodward, P. M.

A-Site Cation Ordering in AA′BB′O6 Perovskite. _J. Solid State Chem._ 179, 1076–1085 (2006). Article  ADS  CAS  Google Scholar  * Vasala, S. & Karppinen, M. A B′B′′O6 perovskites: A

review. _Prog. Solid State Chem._ 43, 1–36 (2015). Article  CAS  Google Scholar  * Serrate, D., De. Teresa, J. M. & Ibarra, M. R. Double perovskites with ferromagnetism above room

temperature. _J. Phys.: Condens. Matter_ 19, 023201 (2007). ADS  Google Scholar  * Chen, G., Pereira, R. & Balents, L. Exotic phases induced by strong spin-orbit coupling in ordered

double perovskites. _Phys. Rev. B_ 82, 174440 (2010). Article  ADS  Google Scholar  * Chen, G. & Balents, L. Spin-orbit coupling in d2 ordered double perovskites. _Phys. Rev. B_ 84,

094420 (2011). Article  ADS  Google Scholar  * Aharen, T. _et al_. Structure and magnetic properties of the S = 1 geometrically frustrated double perovskites La LiReO6 and Ba YReO6. _Phys.

Rev. B_ 81, 064436 (2010). Article  ADS  Google Scholar  * Vries, M. A., de., Mclaughlin, A. C. & Bos, J. W. G. Valence Bond Glass on an fcc Lattice in the Double Perovskite Ba2 YMoO6.

_Phys. Rev. Lett._ 104, 177202 (2010). Article  ADS  Google Scholar  * Aharen, T. _et al_. Magnetic properties of the geometrically frustrated S =1/2 antiferromagnets, La2 LiMoO6 and Ba2

YMoO6, with the B-site ordered double perovskite structure: Evidence for a collective spin-singlet ground state. _Phys. Rev. B_ 81, 224409 (2010). Article  ADS  Google Scholar  * Wiebe, C.

R., Greedan, J. E., Luke, G. M. & Gardner, J. S. Spin-glass behavior in the S = 1/2 fcc ordered perovskite Sr2 CaReO6. _Phys. Rev. B_ 65, 144413 (2002). Article  ADS  Google Scholar  *

Wiebe, C. R. _et al_. Frustration-driven spin freezing in the S = 1/2 fcc perovskite Sr2 MgReO6. _Phys. Rev. B_ 68, 134410 (2003). Article  ADS  Google Scholar  * Erickson, A. S. _et al_.

Ferromagnetism in the Mott Insulator Ba2 NaOsO6. _Phys. Rev. Lett._ 99, 016404 (2007). Article  ADS  CAS  Google Scholar  * Xiang, H. J. & Whangbo, M. H. Cooperative effect of electron

correlation and spin-orbit coupling on the electronic and magnetic properties of Ba2 NaOsO6. _Phys. Rev. B_ 75, 052407 (2007). Article  ADS  Google Scholar  * Yamamura, K., Wakeshima, M.

& Hinatsu, Y. Structural phase transition and magnetic properties of double perovskites Ba2 Ca_M_O6 (_M_ = W, Re, Os). _J. Solid State Chem._ 179, 605–612 (2006). Article  ADS  CAS 

Google Scholar  * Thompson, C. M. _et al_. Long range magnetic order in the 5d2 double perovskite Ba2 CaOsO2: comparison with spin-disordered Ba YReO. _J. Phys.: Condens. Matter_ 26, 306003

(2014). CAS  Google Scholar  * Shannon, R. D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. _Acta Cryst_ A32, 751–767 (1976).

Article  CAS  Google Scholar  * Brese, N. E. & ÓKeeffe, M. Bond-valence parameters for solids. Acta Crystallogr. _Sect. B: Struct. Sci_ 7, 192–197 (1991). Google Scholar  * Medarde, W.

_et al_. _R_NiO3 perovskites (_R_ = Pr, Nd): Nickel valence and the metal-insulator transition investigated by x-ray absorption spectroscopy. _Phys. Rev. B_ 46, 14975 (1992). Article  ADS 

CAS  Google Scholar  * Mott, N. F. Conduction in non-crystalline materials. _Philos. Mag._ 19, 835 (1969). Article  ADS  CAS  Google Scholar  * Alamelu, T., Varadaraju, U. V., Venkatesan,

M., Douvalis, A. P. & Coey, J. M. D. Structural and magnetic properties of (Sr Ca)FeReO. _J. Appl. Phys._ 91, 8909 (2002). Article  ADS  CAS  Google Scholar  * Thompson, C. M. _et al_.

Synthesis, structure, and magnetic properties of novel B-site ordered double perovskites, SrLaMReO6 (M = Mg, Mn, Co and Ni). _Dalton Trans._ 44, 10806–10816 (2015). Article  CAS  Google

Scholar  * Bertaut, E. F., Corliss, L., Forrat, F., Aleonard, R. & Pauthenet, R. Etude de niobates et tantalates de metaux de transition bivalents. _J. Phys. Chem. Solids_ 21, 234–251

(1961). Article  ADS  CAS  Google Scholar  * Goodenough, J. B. Theory of the Role of Covalence in the Perovskite-Type Manganites [La,M(II)MnO3]. _Phys. Rev_ 100, 564 (1955). Article  ADS 

CAS  Google Scholar  * Kanamori, J. Superexchange interaction and symmetry properties of electron orbitals. _J. Phys. Chem. Solids_ 10, 87–98 (1959). Article  ADS  CAS  Google Scholar  *

Iwanaga, D., Inaguma, Y. & Itoh, M. Structure and magnetic properties of Sr2 NiAO6 (A = W, Te). _Mater. Res. Bull._ 35, 449–457 (2000). Article  CAS  Google Scholar  * Gao, H. _et al_.

Structure-property relations in the distorted ordered double perovskite Sr2 InReO6. _Phys. Rev. B_ 83, 134406 (2011). Article  ADS  Google Scholar  * Sikora, M. _et al_. Evidence of

unquenched Re orbital magnetic moment in AA´FeReO6 double perovskites. _Appl. Phys. Lett._ 89, 062509 (2006). Article  ADS  Google Scholar  * Michalik, J. M. _et al_. High-field

magnetization measurements in Sr2 CrReO6 double perovskite: Evidence for orbital contribution to the magnetization. Eur. _Phys. Lett._ 78, 17006 (2007). Google Scholar  * Jeon, B. C. _et

al_. Electronic structure of double perovskite A2 FeReO6 (A = Ba and Ca): interplay between spin-orbit interaction, electron correlation, and lattice distortion. _J. Phys.: Condens. Matter_

22, 345602 (2010). CAS  Google Scholar  * Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. _Physica B_ 192, 55–69 (1993). Article 

ADS  Google Scholar  * Fischer, P. _et al_. High-resolution powder diffractometer HRPT for thermal neutrons at SINQ. _Physica B_ 276–278, 146–147 (2000). Article  ADS  Google Scholar 

Download references ACKNOWLEDGEMENTS This work was supported by the Swedish Research Council, VR, under the contracts 2014-6426, 2016-04524, 2016-06955, and 2017-05078. S.J. and P.A. thanks

Council of Scientific and Industrial Research (CSIR), India for fellowship. P.A.K. thanks the Swedish Foundation for International Cooperation in Research and Higher Education (STINT) for

supporting his stay at Uppsala University. S.R. thanks Indo-Italian POC for support to carry out experiments (20145381) in Elettra, Italy. S.R. also thanks Department of Science and

Technology (DST) [Project No. WTI/2K15/74] and TRC, Department of Science and Technology (DST), Government of India for support. MM and OKF are supported by a Marie Skłodowska Curie Action,

International Career Grant through the European Union . EN is fully funded by the Swedish Foundation for Strategic Research (SSF) within the Swedish national graduate school in neutron

scattering (SwedNess). The experimental neutron diffraction work was performed at the HRPT beamline of the Laboratory for Neutron Scattering & Imaging, Paul Scherrer Institute, CH-5232

Villigen PSI, Switzerland. We thank the beamline staff for their support. Open access funding provided by Uppsala University. AUTHOR INFORMATION Author notes * Somnath Jana Present address:

Institute for Methods and Instrumentation in Synchrotron Radiation Research FG-ISRR, Helmholtz-Zentrum Berlin für Materialien und Energie, Albert-Einstein-Strasse 15, 12489, Berlin, Germany

* P. Anil Kumar Present address: Seagate Technology, 1 Disc Drive, Springtown, Northern Ireland, BT48 0BF, United Kingdom AUTHORS AND AFFILIATIONS * Centre for Advanced Materials, Indian

Association for the Cultivation of Science, Jadavpur, Kolkata, 700032, India Somnath Jana & Sugata Ray * Department of Physics and Astronomy, Uppsala University, 752 36, Uppsala, Sweden

Somnath Jana & Olof Karis * School of Materials Science, Indian Association for the Cultivation of Science, Jadavpur, Kolkata, 700032, India Payel Aich & Sugata Ray * Department of

Engineering Sciences, Uppsala University, 752 36, Uppsala, Sweden P. Anil Kumar & Peter Svedlindh * Department of Applied Physics, KTH Royal Institute of Technology, SE-164 40,

Stockholm, Kista, Sweden O. K. Forslund, E. Nocerino & M. Månsson * Laboratory for Neutron Scattering & Imaging, Paul Scherrer Institute, CH-5232, Villigen, PSI, Switzerland V.

Pomjakushin * UGC-DAE-Consortium for Scientific Research Mumbai Centre, 246C 2nd floor Common Facility Building (CFB), Bhabha Atomic Research Centre, Mumbai, 400085, India Vasudeva Siruguri

* Department of Physics Chalmers University Of Technology, SE-412 96, Gteborg, Sweden Y. Sassa Authors * Somnath Jana View author publications You can also search for this author inPubMed 

Google Scholar * Payel Aich View author publications You can also search for this author inPubMed Google Scholar * P. Anil Kumar View author publications You can also search for this author

inPubMed Google Scholar * O. K. Forslund View author publications You can also search for this author inPubMed Google Scholar * E. Nocerino View author publications You can also search for

this author inPubMed Google Scholar * V. Pomjakushin View author publications You can also search for this author inPubMed Google Scholar * M. Månsson View author publications You can also

search for this author inPubMed Google Scholar * Y. Sassa View author publications You can also search for this author inPubMed Google Scholar * Peter Svedlindh View author publications You

can also search for this author inPubMed Google Scholar * Olof Karis View author publications You can also search for this author inPubMed Google Scholar * Vasudeva Siruguri View author

publications You can also search for this author inPubMed Google Scholar * Sugata Ray View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS S.J.

and P.A. contributed equally. S.J. designed the project and the method of synthesis. S.J. and P.A. have synthesized and characterized the compounds. S.J. and P.A. have performed the XAS and

_R_ vs _T_ measurements and analysis. The magnetic measurements and analysis are performed by S.J., P.A., P.A.K. and P.S., while O.K.F., E.N., V.P., M.M. and Y.S. have performed the NPD

measurements. O.K. has helped in performing x-ray absorption spectroscopy and contributed in discussion. V.S. has done the NPD analysis and the combined NPD and XRD refinement. S.J., P.A.

and S.R. wrote the main body of the manuscript, while all the authors contributed in writing and reviewing the manuscript. CORRESPONDING AUTHOR Correspondence to Somnath Jana. ETHICS

DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in

published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons

Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original

author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the

article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use

is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Jana, S., Aich, P., Kumar, P.A. _et al._ Revisiting Goodenough-Kanamori rules in a

new series of double perovskites LaSr1−_x_Ca_x_NiReO6. _Sci Rep_ 9, 18296 (2019). https://doi.org/10.1038/s41598-019-54427-0 Download citation * Received: 23 August 2018 * Accepted: 13

November 2019 * Published: 04 December 2019 * DOI: https://doi.org/10.1038/s41598-019-54427-0 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content:

Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative