3d-printed sound absorbing metafluid inspired by cereal straws

ABSTRACT Used as building biomaterials for centuries, cereal straws are known for their remarkable acoustic performances in sound absorption. Yet, their use as fibrous media disregards their

internal structure made of nodes partitioning stems. Here, we show that such nodes can impart negative acoustic bulk modulus to straw balls when straws are cut on either side of a node.

Such metafluid inspired by cereal straws combines visco-thermal diffusion with strong wave dispersion arising from quarter-wavelength resonances within straws. Large spectral bandgaps and

slow sound regimes are theoretically predicted and experimental data from impedance tube measurements on an idealised 3D-printed sample layer are in good agreement with the theoretical

model. Perfect absorption is achieved at wavelengths 13 times larger than the thickness of the metafluid layer, and slow sound entails an increased density of states causing a cascade of

high absorption peaks. Such features could lead cereal straws to serve as cheap acoustic bio-metamaterials. SIMILAR CONTENT BEING VIEWED BY OTHERS SUBWAVELENGTH BROADBAND SOUND ABSORBER

BASED ON A COMPOSITE METASURFACE Article Open access 14 August 2020 DECORATED BACTERIA-CELLULOSE ULTRASONIC METASURFACE Article Open access 01 September 2023 INVESTIGATION OF FACTORS

AFFECTING THE SOUND ABSORPTION BEHAVIOUR OF 3D PRINTED HEXAGONAL PRISM LATTICE POLYAMIDE STRUCTURES Article Open access 28 December 2024 INTRODUCTION Recent developments in manufacturing

techniques, such as Fused Filament Fabrication and Stereolithography technologies, have considerably broadened the range of possible architectures for artificial materials1. Advanced

material properties have subsequently been tailored in many fields of physics, among which pentamode mechanics2, acoustic rainbow trapping3, metasurface retroreflector4, or microwave atomic

clock5. From this perspective, biological systems can be a valuable source of inspiration: idealised synthetic replicas mimicking fauna and flora6, spider-web structures7, or sperm-cell

motion8 have demonstrated astonishing performances in photonics, lattice mechanics, and micro-robotics. Particularly interesting in acoustic and thermal insulation are cereal straws such as

wheat, reed or rattan. They have been used as building materials for centuries due to their large availability throughout the world. Previous empirical9, phenomenological10, and

theoretical11 studies showed that viscous and thermal diffusion through the arrangement of stems play a dominant role in acoustic performances. Attention was mainly paid to the effects of

the length, concentration, and relative orientations of the straws on sound absorption. While arrays of straws were usually idealised as classical visco-thermal fluids made of either solid

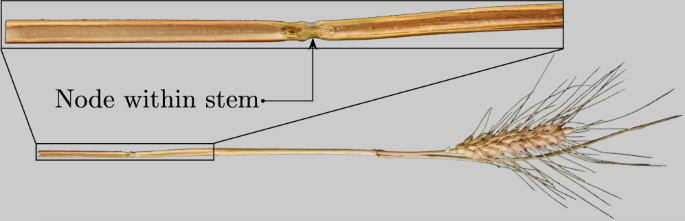
or completely hollow straws, closer examination of cereal straws in Fig. 1 reveals that nodes within the stem partition the straw into tubular segments. Therefore, when cutting straws on

either side of a node, the resulting pieces are neither solid obstacles in the path of the acoustic wave, nor open hollow straws channelling the flow, but rather double quarter-wavelength

resonators (QWR) separated by the node. Based on this observation, we designed a metafluid inspired by the cereal straws (MCS) made of the periodic repetition of double QWR, see Fig. 2. We

theoretically show that their collective resonances entail an effective negative bulk modulus in the MCS around the QWR fundamental frequency resulting in both band gap opening and strong

wave dispersion. In particular, the strong dispersion induced by the double QWR below its fundamental resonance generates a slow propagation of sound over a wide band in the low frequencies.

Therefore, the Fabry-Perot resonances of a MCS layer appear in the deep subwavelength regime and its associated density of states is increased. Combining these effects with the viscous and

thermal diffusion tailored by the concentration of double QWR, each low quality factor mode of the MCS layer can yield perfect absorption peaks due to a critical coupling between the

inherent losses and the energy leakage of the MCS layer12. The theoretical predictions are supported experimentally by data from impedance tube measurements on prototypes fabricated by Fused

Filament Fabrication. This manufacturing technique induces corrugation at the walls of the straws which has been advantageously used to enhance further attenuation in the manufactured

sample. Perfect absorption of sound for wavelengths in air 13 times larger than the layer thickness has been achieved with large absorption value below the first resonance of the double QWR.

IDEALISATION OF THE CEREAL STRAW ARRANGEMENT The cereal straw arrangement is idealised by a three-dimensional \({\rm{\Omega }}\)-periodic repetition of straight double QWR, as shown in Fig.

 2. The unit cell \({\rm{\Omega }}\) is a rectangular cube with the dimensions \({\ell }_{1}\times {\ell }_{2}\times {\ell }_{3}\) in the directions of the Cartesian coordinate system

\(({{\bf{e}}}_{1},{{\bf{e}}}_{2},{{\bf{e}}}_{3})\) containing a double QWR. The axis of each double QWR is oriented along the direction E1 and consecutive stacks of straws are separated by

an air-gap to permit air to flow inside the straws. Each double QWR has the outer radius _r__o_, the inner radius \({r}_{i} < {r}_{o}\), and the finite length \(h\le {\ell }_{1}\). The

volume of the double QWR is split by a rigid node into two cylindrical ducts \({{\rm{\Omega }}}_{1}\) and \({{\rm{\Omega }}}_{2}\) with the lengths _h_1 and _h_2 and the outside apertures

\({{\rm{\Sigma }}}_{1}\) and \({{\rm{\Sigma }}}_{2}\) respectively. Denoting by \({{\rm{\Omega }}}_{0}\) the air domain of the unit cell outside the straw, the filling fractions \({\varphi

}_{0}=|{{\rm{\Omega }}}_{0}|/|{\rm{\Omega }}|\), \({\varphi }_{1}=|{{\rm{\Omega }}}_{1}|/|{\rm{\Omega }}|\) and \({\varphi }_{2}=|{{\rm{\Omega }}}_{2}|/|{\rm{\Omega }}|\) are defined and the

total porosity of the arrangement is \(\varphi ={\varphi }_{0}+{\varphi }_{1}+{\varphi }_{2}\). Besides, the outside walls of the straw are supposed to be corrugated periodically with the

period \({\ell }_{c}\) in the direction E1 and the semi-elliptic profile of height _h__c_ in a longitudinal cross-section, see Fig. 2(d). Although, this corrugation is not fundamental to the

singular behaviour of the metafluid, it is an inherent side-effect of the layer-by-layer 3D-printing process using Fused Filament Fabrication technology. It must be accounted for

theoretically in the present case of tightly-packed straw arrangements, for which the corrugation height _h__c_ is of the same order as the spacing \({\ell }_{2}-2{r}_{o}\) between two

neighbouring straws. SOUND PROPAGATION IN THE MCS The propagation of air-borne acoustic waves in the MCS is studied under ambient conditions in the linear harmonic regime at frequencies

\(\omega \) with the implicit time factor \({e}^{-{\rm{i}}\omega t}\). Under the assumption that lattice sizes \({\ell }_{1}\), \({\ell }_{2}\), \({\ell }_{3}\) are sufficiently small

compared to the wavelength \({\lambda }_{e}=2\pi \)/\({k}_{e}\) in air (typically below the Bragg limit \({\ell }_{1}\le {\lambda }_{e}\)/2), the idealised system is expected to behave as a

metafluid, that is an effective homogeneous medium with strong wave dispersion induced by microstructural QWR resonances. The effective pressure _P_ and particle velocity V in the MCS are

governed by the following equations of mass conservation and generalized Darcy law, see Section Methods for details, $$\nabla \cdot {\bf{V}}={\rm{i}}\omega

P/B,\,{\rm{and}}\,{\bf{V}}=-\,{\bf{K}}\nabla P/\eta ,$$ (1) where _η_ is the viscosity in air and where both the effective bulk modulus _B_ and the Darcy permeability tensor K are

complex-valued and frequency dependent. In particular, the Darcy tensor is diagonal in the coordinate system \(({{\bf{e}}}_{1},{{\bf{e}}}_{2},{{\bf{e}}}_{3})\) due to the symmetries of the

unit cell \({\rm{\Omega }}\), $${\bf{K}}={K}_{1}\,{{\bf{e}}}_{1}\otimes {{\bf{e}}}_{1}+{K}_{2}\,{{\bf{e}}}_{2}\otimes {{\bf{e}}}_{2}+{K}_{3}\,{{\bf{e}}}_{3}\otimes {{\bf{e}}}_{3},$$ (2)

where the principal permeabilities _K__n_ with \(n\in \{1,2,3\}\) are expressed by the Johnson formula13, and the homogenisation theory14,15, see Section Methods. The effective bulk modulus

_B_ satisfies the following association rule when normalised by the bulk modulus _B__e_ of air, $${B}^{-1}={B}_{e}^{-1}({\varphi }_{0}{\beta }_{0}+{\varphi }_{1}{\beta }_{1}+{\varphi

}_{2}{\beta }_{2}),$$ (3) where _β_0 is the compressibility factor considering the thermo-acoustic phenomena in the domain \({{\rm{\Omega }}}_{0}\), and _β_1 and _β_2 are apparent

compressibility factors induced by the resonances in the domains \({{\rm{\Omega }}}_{1}\) and \({{\rm{\Omega }}}_{2}\). While _β_0 is given by the Johnson-Lafarge model13,16 and the

homogenisation theory14,15, the apparent compressibility factors _β_1 and _β_2 account for the fact that the QWRs act as secondary acoustic sources in the medium, see Section Methods. They

can be expressed in the form, $${\beta }_{j}={(\frac{{B}_{j}}{{B}_{e}}\frac{{k}_{j}{h}_{j}}{\tan ({k}_{j}{h}_{j})}-\mu {k}_{e}^{2}{r}_{i}{h}_{j})}^{-1},\,j\in \{1,2\},$$ (4) where

\({k}_{j}=\omega /\sqrt{{B}_{j}/{\rho }_{j}}\) is the wavenumber in the domain \({{\rm{\Omega }}}_{j}\), with the effective density \({\rho }_{j}\) and bulk modulus _B__j_ in \({{\rm{\Omega

}}}_{j}\) being derived from the Zwikker & Kosten model17. Moreover, the dimensionless factor \(\mu =1.2\) in Eq. (4) corrects the radiation impedance at the aperture \({{\rm{\Sigma

}}}_{j}\). Hence, the quarter-wavelength resonance of the duct \({{\rm{\Omega }}}_{j}\) can cause _β__j_ and thus the bulk modulus _B_ to become negative18,19, which offers the possibility

to open non-propagative band-gaps and generate slow sound regimes. Moreover, since the inner resonances only affect the mass conservation, non-propagative band-gaps are opened for any

direction of propagation in the MCS, regardless of the anisotropy of the Darcy tensor. EFFECTIVE FLUID PARAMETERS OF THE MCS The MCS with the following geometry is considered,

$$\{\begin{array}{lll}{\ell }_{1}=41\,{\rm{mm}}, & {\ell }_{2}=8.4\,{\rm{mm}}, & {\ell }_{3}=8.4\,{\rm{mm}},\\ h=40\,{\rm{mm}}, & {h}_{1}=30\,{\rm{mm}}, &

{h}_{2}=10\,{\rm{mm}},\\ {r}_{o}=4.0\,{\rm{mm}}, & {r}_{i}=3.8\,{\rm{mm}}, & \\ {\ell }_{c}=209\,\mu {\rm{m}}, & {h}_{c}=77\,\mu {\rm{m}}. & \end{array}$$ (5) A photograph of

the 3D-printed MCS prototype manufactured by means of Fused Filament Fabrication is shown in Fig. 3(a). To characterise the corrugation at the outer walls of the straws and estimate \({\ell

}_{c}\) and _h__c_, a cliché by Electron Scan Microscopy is presented in Fig. 3(b). It bears testament to the fact that the corrugation height _h__c_ is of the same order as the spacing

\({\ell }_{2}-2{r}_{o}\approx 400\,\mu {\rm{m}}\) between two neighbouring straws. While the corrugation parameters \({\ell }_{c}\) and _h__c_ are prescribed by the 3D-printer, the other

geometrical parameters in Eq. (5) result from an optimisation procedure presented in Section Methods. It is worth noting here that such geometry with \({\ell }_{2}={\ell }_{3}\) entails the

orthotropy of the Darcy tensor, with the principal permeabilities _K_2 and _K_3 being equal in Eq. (2). Figure 4(a,b) represent the effective normalised parameters \(\varphi B\)/\({P}_{e}\)

and \(-{\rm{i}}\omega {\rho }_{e}{K}_{n}\)/\(\eta \) with \(n\in \{1,2\}\) for the MCS, where _P__e_ is the atmospheric pressure and \({\rho }_{e}\) the density of air. For the sake of

comparison, both quantities in the absence of the QWR, that is when \({r}_{i}=0\) and hence \({\varphi }_{j}=0\) for \(j\in \{1,2\}\), are also plotted. This latter system can be seen as a

equivalent anisotropic fluid inspired by cereal straws (FCS)20. As shown in Fig. 4(a) and emphasised in the lower inset, the fundamental resonance of the double QWR induces negative bulk

modulus _B_ over the broad frequency range \([2460,3254]\,{\rm{Hz}}\). The low frequency limit of the bulk modulus is also magnified in the upper inset, which shows the transition between

the isothermal and adiabatic regimes of the MCS around the characteristic thermal frequency _ω__θ_/2_π_ ≈ 8.24 Hz13,16. Compared to the QWR resonance, this thermal transition occurs at much

lower frequencies and with much smaller impact on the effective bulk modulus. Figure 4(b) represents the complex and frequency dependent Darcy permeabilities of the MCS. Note that the Darcy

permeabilities of the FCS are the same as those of the MCS. Differences between _K_1 and _K_2 clearly show the anisotropic behaviour of the system. The frequencies _ω_1/2_π_ ≈ 6 Hz and

_ω_2/2_π_ ≈ 83 Hz characterise the transition between the viscodiffusive regime and the inertio-propagative regime in the principal directions E1 and E213,16. DISPERSION RELATION IN THE MCS

To show the effects of the effective fluid parameters on wave propagation, the dispersion relation in both the MCS and the FCS is studied. In each principal direction E_n_ with _n_ ∈ {1, 2,

3}, the wavenumber _k__n_ and the sound speed _c__n_ are given by _k__n_ = _ω_/_c__n_ and \({c}_{n}=\sqrt{-{\rm{i}}\omega {K}_{n}B/\eta }\), where _c_2 = _c_3 due to the orthotropy in the

system. The real and imaginary parts of the wavenumbers \({k}_{n}^{MCS}\) in the MCS, \({k}_{n}^{FCS}\) in the FCS and _k__e_ in air are shown in Fig. 5(a,b) while the normalized sound

speeds Re(_c__n_)/_c__e_ are shown Fig. 5(c), where _c__e_ is the sound speed in air. First of all, the anisotropy in the MCS and the FCS entails different dispersion relations according to

the principal direction E_n_ with _n_ ∈ {1, 2, 3}. However, in each principal direction, a band gap is opened for the MCS in the frequency range where the effective bulk modulus has negative

values. This band gap is characterised by quasi non-propagative waves, \({\rm{Re}}({k}_{n}^{MCS})\to 0\), with characteristic attenuation length 1/\({\rm{Im}}({k}_{n}^{MCS})\) much shorter

than the wavelength 2_π_/\({\rm{Re}}({k}_{n}^{MCS})\), and vanishing sound speed \({\rm{Re}}({c}_{n}^{MCS})\to 0\). At frequencies below the band gap, the wave speeds are much smaller than

the wave speed in both the FSC and the air, resulting in a slow sound regime. In this regime, the wave speeds possess a plateau at low frequencies and slowly decrease to a value close to

zero at the frequency of the lower bound of the band gap. It is worth noting that the group velocity, defined as \({v}_{g}=\partial \omega \)/\(\partial {k}_{n}^{MCS}\) is also much lower

than the group velocity in both the FCS and in air and tend to zero at the frequency of the lower bound of the band gap. We notice also that the inherent losses of the MCS, translating in

Im(_k__n_), are not negligible for the frequencies below the band gap. At frequencies above the band gap the wave speed is higher than that of both the FSC and the air, resulting in a

supersonic regime19,21,22. Conversely, the wave dispersion and attenuation in the FCS are weak in every direction: the sound speed along the principal directions are almost constant in the

inertial-adiabatic regime above 100 Hz, with the sound speed being close to that of air in the direction E1 but almost divided by 2 along the directions E2 due to a tortuosity effect. For

both the FCS and the MCS, the sound speed decreases down to zero as _ω_ → 0 in the viscous regime below 100 Hz. CRITICAL COUPLING AND PERFECT ABSORPTION The slow sound effect and the

inherent losses of the MCS discussed before can be used to design finite size perfect absorber samples. On the one hand, the frequencies of the Fabry-Perot resonances drastically decrease

due to the slow sound regime of the MCS. As a consequence, these resonances happen for wavelengths much larger than the structure thickness, i.e., the MCS becomes deeply sub-wavelength. On

the other hand, the MCS layer behaves as an open lossy and resonant system, characterised at the resonant frequencies, by both the leakage rate of energy (i.e., the coupling of the resonant

elements with the propagating medium) and the inherent losses. In the reflection problem, the balance between the leakage and the losses activates the condition of critical coupling,

enabling a perfect impedance matching to the background medium, and therefore generating a perfect energy absorption12,22,23. The layer sample analysed here and depicted in Fig. 3 has been

designed so that the layer of thickness _L_ = 13\({\ell }_{3}\) = 109.2 mm is critically coupled to air under plane wave excitation at normal incidence with _λ__e_ = 13 _L_ in the principal

direction E3, see Section Methods. In a reflection problem, the representation of the zeros and the poles of the reflection coefficient in the complex frequency plane is an efficient tool to

interpret the critical coupling condition12. Introducing the complex frequency plane (complex frequency \(\tilde{\omega }=\omega +{\rm{i}}{\omega }_{{\rm{Im}}}\)), the reflection

coefficient, \(R(\tilde{\omega })\), represents the scattering of the system. In the lossless case, the relation \({R}^{\ast }(\tilde{\omega })=1\)/\(R({\tilde{\omega }}^{\ast })\) is

satisfied due to temporal invariance symmetry, where \({R}^{\ast }(\tilde{\omega })\) and \({\tilde{\omega }}^{\ast }\) are the complex conjugate of \(R(\tilde{\omega })\) and

\(\tilde{\omega }\) respectively. Consequently, the reflection coefficient possesses pairs of poles and zeros at complex frequencies being complex conjugate with each other. More

importantly, the imaginary part of the complex frequency of the pole represents the energy leakage of the system. In the lossy case, when inherent losses are introduced, the zeros and poles

are not complex conjugates any more and in particular both are shifted downward in the complex frequency plane, if _e_−i_ωt_ is used. The zero of the reflection coefficient can thus

intersect the real frequency axis, enabling perfect absorption when exactly located on this axis. Figure 6(a) shows the complex frequency plane for the FCS sample. The pairs of pole/zero

represent the different Fabry-Perot resonances of the system. Complementary, Fig. 6(b) depicts the theoretical predictions and the experimental results of the absorption coefficient for the

FCS sample. Both the pairs of pole/zero and the absorption peaks appear almost equally spaced in frequency, approximatively following the typical harmonic series {1, 3, 5, 7, …} of the

quarterwavelength resonances of a rigidly backed layer, because the system is weakly dispersive (as shown in Fig. 5(a,b)). Moreover, the distance of the zero of the reflection coefficient to

the real frequency axis is related to the amplitude of the absorption peaks: the closer the zero to the real frequency axis, the higher the absorption peak. Notably, a near-perfect

absorption (97.4%) is observed experimentally on the first peak at 509 Hz. Experimental results are in very good agreement with the theoretical predictions. Figure 6(c,d) respectively show

the complex frequency plane and the absorption coefficient for the MCS sample. The absorption peaks and the pairs pole/zero are not any more equally spaced in frequency due to the strong

dispersion introduced by the resonances of the double QWR. Here, we pay attention to the frequencies below the band gap. The first absorption peak appears at 272 Hz. The ratio of the wave

speed between the FCS and the MCS along the E2 (=E3) direction [in Fig. 5(c)] is in good agreement with the downshifting of this peak at low frequencies with respect to the first absorption

peak of the FCS. More importantly, we observe perfect absorption for this peak (experimentally 99.6% at 258 Hz), where the corresponding wavelength equals to 13 times the slab thickness.

Thus, this system represents a sub-wavelength perfect absorber. A cascade of nearly perfect absorption peaks, due to the higher order Fabry-Perot resonances, is produced and perfectly

grasper by the theory. Each of these nearly perfect absorption peak is associated with a low quality factor resonance arising from the coupling with viscous and thermal diffusion tailored by

the concentration of double QWR and the corrugation. These low quality factors strongly contribute to enhance the absorption between two consecutive peaks. Nevertheless, a perfect

absorption peak theoretically predicted at the lower bound of the band gap around 2.39 kHz is in disagreement with the experimental data, in which an absorption coefficient of 0.86 is

achieved. This is due to the fact that the theoretical model assumes an infinite number of the resonators along the structure depth, creating an accumulation point24, while this number is

finite in practice. Effectively, the MCS sample comprises only 13 unit cells along the E3 direction. CONCLUSIONS The metafluid inspired by cereal straws has been theoretically and

experimentally reported for sub-wavelength perfect sound absorption. A straw bale constituted of straws cut on either side of a node is idealized by a three-dimensional periodic repetition

of tightly packed double QWR. This idealised straw bale is homogenised, exhibiting slow sound region enabling to increase of the density of state in the subwavelength regime together with

viscous and thermal diffusion through the arrangement of stems. The MCS behaves like an open and lossy resonator, the absorption properties of which are tailored by critical coupling.

Therefore, the designed MSC is a sub-wavelength perfect absorber. Moreover, the strong dispersion arising from the fundamental resonance of the double QWR induces a cascade of nearly perfect

absorption peaks below the lower bound of the band gap. The absorption between consecutive peaks is strongly enhanced by the viscous and thermal diffusion through the anisotropic

surrounding fluid. The designed MCS possess a 99.6% absorption peak at 258 Hz, which corresponds to a wavelength 13 times larger than of the slab thickness. The design of the present MSC

offers both a comprehensive explanation of the acoustic properties of bio-sourced materials, such as wheat, reed, or rattan and large perspectives for the design of bio-inspired metafluid,

notably through its anisotropy. METHODS The density \({\rho }_{e}=1.213\) kg/m3, adiabatic constant \(\gamma =1.4\), thermal conductivity \(\kappa =2.5\times {10}^{-2}\) W/m/K, isobaric heat

capacity \({C}_{p}=1.219\times {10}^{3}\) J/K, and viscosity \(\eta =1.839\times {10}^{-5}\) Pa.s were used for air at equilibrium, as well as the atmospheric pressure \({P}_{e}=1.013\times

{10}^{5}\) Pa, the bulk modulus \({B}_{e}=\gamma {P}_{e}\), the sound speed \({c}_{e}=\sqrt{{B}_{e}/{\rho }_{e}}\) and the air wavenumber \({k}_{e}=\omega \)/_c__e_. PORO-ACOUSTICS WITH

INNER RESONANCES Using the theory of poro-acoustics with inner resonances19, the effective pressure _P_ and particle velocity V in the MCS are governed by the following equations of mass

conservation and generalised Darcy law, $$\nabla \cdot {\bf{V}}={\rm{i}}\omega \frac{{\varphi }_{0}{\beta }_{0}}{{B}_{e}}P+\frac{{Q}_{1}+{Q}_{2}}{|{\rm{\Omega

}}|},\,{\bf{V}}=-\,\frac{{\bf{K}}}{\eta }\nabla P,$$ (6) where _Q__j_ is the flux pulsed out from the aperture \({{\rm{\Sigma }}}_{j}\), and where the compressibility factor _β_0 in

\({{\rm{\Omega }}}_{0}\) is driven by the thermal permeability \({\rm{\Theta }}\) according to, $${\beta }_{0}=\gamma +{\rm{i}}\omega \,(\gamma -1)\,{\rm{\Theta }}\,{C}_{p}/({\varphi

}_{0}\kappa ).$$ (7) Equation (6) reveals that the QWRs act as secondary acoustic sources in the mass conservation: they radiate the flux \({Q}_{1}+{Q}_{2}\) in the effective medium formed

by the array of straws, as these latter modify the air flow path. Conversely to the case of FCS for which \({Q}_{1}={Q}_{2}=0\), the presence of the nodes within the straws makes each duct

\({{\rm{\Omega }}}_{j}\) behave as a QWR emitting the flux, $${Q}_{j}=\frac{|{{\rm{\Sigma }}}_{j}|P}{1/{Y}_{j}+{\rm{i}}\omega {\rho }_{e}\mu

{r}_{i}}\,{\rm{with}}\,{Y}_{j}=\frac{{\rm{i}}\omega \,\tan ({k}_{j}{h}_{j})}{{k}_{j}{B}_{j}},$$ (8) where \(|{{\rm{\Sigma }}}_{j}|=|{{\rm{\Omega }}}_{j}|\)/_h__j_ is the surface area of the

apertures, _Y__j_ is the surface admittance at the aperture \({{\rm{\Sigma }}}_{j}\). Substitution of Eq. (8) into (6) results in the equations of effective mass conservation and Darcy law

in the MCS presented in Eq. (1). Furthermore, the effective density and bulk modulus of air in the ducts \({{\rm{\Omega }}}_{j}\) with \(j\in \{1,2\}\) satisfy Zwikker & Kosten model17:

$$\frac{{\rho }_{j}}{{\rho }_{e}}=-\,\frac{{{\bf{J}}}_{0}({X}_{v})}{{{\bf{J}}}_{2}({X}_{v})},\,\frac{{B}_{e}}{{B}_{j}}=\gamma +(\gamma

-1)\frac{{{\bf{J}}}_{2}({X}_{t})}{{{\bf{J}}}_{0}({X}_{t})},$$ (9) where J0 and J2 are Bessel functions of the first kind and order 0 and 2, while \({X}_{v}={r}_{i}\sqrt{{\rm{i}}\omega {\rho

}_{e}/\eta }\) and \({X}_{t}={r}_{i}\sqrt{{\rm{i}}\omega {C}_{p}/\kappa }\) represent the duct radius normalized by the viscous and thermal skin-depths. Thermal permeability \({\rm{\Theta

}}\) and principal Darcy permeabilities _K__n_ with \(n\in \{1,2,3\}\), are given by Johnson formula13,16, $${K}_{n}={K}_{n}^{0}/(\sqrt{1-{\rm{i}}\omega {(2{\delta }_{n}/{{\rm{\Lambda

}}}_{n})}^{2}/{\omega }_{n}}-{\rm{i}}\omega /{\omega }_{n}),$$ (10) $${\rm{\Theta }}={{\rm{\Theta }}}^{0}/(\sqrt{1-{\rm{i}}\omega {(2{\delta }_{\theta }/{{\rm{\Lambda }}}_{\theta

})}^{2}/{\omega }_{\theta }}-{\rm{i}}\omega /{\omega }_{\theta }),$$ (11) where \({\omega }_{n}\) and \({\omega }_{\theta }={\mathscr{O}}({\omega }_{n})\) are characteristic viscous and

thermal frequencies, \({\delta }_{n}=\sqrt{\eta /({\rho }_{e}{\omega }_{n})}\) and \({\delta }_{\theta }=\sqrt{\kappa /({C}_{p}{\omega }_{\theta })}\) are viscous and thermal skin depths at

these characteristic frequencies, \({{\rm{\Lambda }}}_{n}\) and \({{\rm{\Lambda }}}_{\theta }\) are characteristic viscous and thermal lengths and \({K}_{n}^{0}\) and \({{\rm{\Theta

}}}^{0}\) are the static values of _K__n_ and \({\rm{\Theta }}\) as \(\omega \to 0\). The characteristic frequencies \({\omega }_{n}\) and \({\omega }_{\theta }\) are defined by: $${\omega

}_{n}={\varphi }_{0}\eta /({K}_{n}^{0}{\rho }_{e}{\tau }_{n}^{\infty }),\,{\omega }_{\theta }={\varphi }_{0}\kappa /({{\rm{\Theta }}}^{0}{C}_{p}),$$ (12) where \({\tau }_{n}^{\infty }\) is

the high frequency tortuosity related to _K__n_. CELL PROBLEMS Following two-scale asymptotic homogenisation14,15, the parameters \({{\rm{\Theta }}}^{0}\) and \({{\rm{\Lambda }}}_{\theta }\)

characterising the thermal behaviour, and \({K}_{n}^{0}\), \({{\rm{\Lambda }}}_{n}\) and \({\tau }_{n}^{\infty }\) characterising the visco-inertial behaviour are given as volume and

surface averages of \({\rm{\Omega }}\)-periodic tests fields _θ_, U_n_ and _χ__n_ defined on the air domain \({{\rm{\Omega }}}_{0}\): $${{\rm{\Theta }}}^{0}=\frac{1}{|{\rm{\Omega

}}|}\mathop{\int }\limits_{{{\rm{\Omega }}}_{0}}\,\theta \,{\rm{d}}{\rm{\Omega }},\,{K}_{n}^{0}=\frac{1}{|{\rm{\Omega }}|}\,\mathop{\int }\limits_{{{\rm{\Omega }}}_{0}}\,{{\bf{u}}}_{n}\cdot

{{\bf{e}}}_{n}\,{\rm{d}}{\rm{\Omega }},$$ (13a) $${{\rm{\Lambda }}}_{\theta }=2\frac{|{{\rm{\Omega }}}_{0}|}{|{{\rm{\Gamma }}}_{0}|},\,{{\rm{\Lambda }}}_{n}=2\frac{{\int }_{{{\rm{\Omega

}}}_{0}}{({{\bf{e}}}_{n}-\nabla {\chi }_{n})}^{2}\,{\rm{d}}{\rm{\Omega }}}{{\int }_{{{\rm{\Gamma }}}_{0}}{({{\bf{e}}}_{n}-\nabla {\chi }_{n})}^{2}\,{\rm{d}}{\rm{\Gamma }}},$$ (13b) $${\tau

}_{n}^{\infty }=|{{\rm{\Omega }}}_{0}|/\,\mathop{\int }\limits_{{{\rm{\Omega }}}_{0}}1-\nabla {\chi }_{n}\cdot {{\bf{e}}}_{n}\,{\rm{d}}{\rm{\Omega }},$$ (13c) where _θ_, U_n_ and _χ__n_

satisfy the following cell problems, with _χ__n_ and \({\zeta }_{n}\) having zero mean values over \({{\rm{\Omega }}}_{0}\): $${\rm{\Delta }}\theta =-\,1,\,\theta =0\,{\rm{on}}\,{{\rm{\Gamma

}}}_{0},$$ (14a) $${\rm{\Delta }}{{\bf{u}}}_{n}=\nabla {\zeta }_{n}-{{\bf{e}}}_{n},\,\nabla \cdot {{\bf{u}}}_{n}=0,\,{{\bf{u}}}_{n}=0\,{\rm{on}}\,{{\rm{\Gamma }}}_{0},$$ (14b) $${\rm{\Delta

}}{\chi }_{n}=0,\,(\nabla {\chi }_{n}-{{\bf{e}}}_{n})\cdot {\bf{n}}=0\,{\rm{on}}\,{{\rm{\Gamma }}}_{0}.$$ (14c) In Eqs (13) and (14), vector N is normal to the boundary \({{\rm{\Gamma

}}}_{0}={{\rm{\Sigma }}}_{1}\cup {{\rm{\Sigma }}}_{2}\cup {{\rm{\Sigma }}}_{{\rm{lat}}}\) where \({{\rm{\Sigma }}}_{{\rm{lat}}}\) is the lateral surface of the straws. The cell problems (14)

are computed numerically by means of the Finite Element Method using commercial software COMSOL Multiphysics®. The computations are performed in 3-D on a single unit cell with periodicity

conditions. Problems in Eq. (14a) and (14c) are solved with module _Coefficient Form PDE_ in _Mathematics_ while problem in Eq. (14b) is solved with module _Creeping flow_ in _Fluid Flow_.

The geometry has been meshed with Free Tetrahedral elements, sufficiently small to ensure accuracy. To account for the corrugation on the cell problems, similar cell problems are computed

for the square array of infinite cylinders with corrugated lateral surface and values of the tests-fields hence obtained are substituted into Eq. (13) in the domain between the cylinders,

while values of _θ_, U_n_ and _χ__n_ in the air gap of thickness \({\ell }_{1}-h\) in the direction E1 is kept unchanged. A corrugation profile in the form of semi-ellipses in a radial

cross-section is considered in the computations. It leads to: $$\{\begin{array}{lll}{\varphi }_{0}=0.284, & {{\rm{\Theta }}}^{0}=0.11\,{{\rm{mm}}}^{2}, & {{\rm{\Lambda }}}_{\theta

}=1.1\,{\rm{mm}},\\ {\tau }_{1}^{\infty }=1.06, & {K}_{1}^{0}=0.11\,{{\rm{mm}}}^{2}, & {{\rm{\Lambda }}}_{1}=1.4\,{\rm{mm}},\\ {\tau }_{2}^{\infty }=2.07, &

{K}_{2}^{0}=0.004\,{{\rm{mm}}}^{2}, & {{\rm{\Lambda }}}_{2}=0.4\,{\rm{mm}},\end{array}$$ (15) for both MCS and FCS analysed in this work. To emphasize the effects of the corrugation, the

parameters calculated for the smooth surface (\({h}_{c}=0\)) were: $$\{\begin{array}{lll}{\varphi }_{0}=0.30, & {{\rm{\Theta }}}^{0}=0.14\,{{\rm{mm}}}^{2}, & {{\rm{\Lambda

}}}_{\theta }=1.6\,{\rm{mm}},\\ {\tau }_{1}^{\infty }=1.06, & {K}_{1}^{0}=0.14\,{{\rm{mm}}}^{2}, & {{\rm{\Lambda }}}_{1}=1.6\,{\rm{mm}},\\ {\tau }_{2}^{\infty }=2.07, &

{K}_{2}^{0}=0.007\,{{\rm{mm}}}^{2}, & {{\rm{\Lambda }}}_{2}=0.7\,{\rm{mm}}.\end{array}$$ (16) SAMPLES AND EXPERIMENTAL SET-UP The reflection of a plane wave from a layer of material of

thickness _L_ arranged against a rigid backing is studied. The air/layer interface \({{\rm{\Gamma }}}_{L}^{0}\) is located at \({x}_{3}=0\), and the rigid backing \({{\rm{\Gamma

}}}_{L}^{b}\) at \({x}_{3}=-\,L\). Both interfaces have the normal vector E3 which is principal direction of the Darcy tensor. Moreover, normal incidence is considered, so that the pressure

reflection coefficient and absorption coefficient read as \(R=(1-\Upsilon )\)/\((1+\Upsilon )\) and \({\mathscr{A}}=1-|R{|}^{2}\) where the normalised admittance \(\Upsilon \) of the layer

reads as follows, $$\Upsilon =-\,{\rm{i}}\,[{B}_{e}{c}_{3}/(B{c}_{e})]\,\tan (\omega L/{c}_{3}).$$ (17) The MCS geometrical parameters were tuned using optimisation Sequential Quadratic

Programming. The minimised cost function is |_R_|2 at the required frequency. The MCS and FCS samples were fabricated using a MakerBot ®Replicator ®2X Experimental 3D Printer based on the

Fused Filament Fabrication technology. Heated continuous filament of thermoplastic material is deposited layer-by-layer by the extruder head having a 400 _μ_m diameter nozzle. The layer

height setting is 200 _μ_m, which corresponds to the period measured on the ESM cliché in Fig. 3. Impedance tube measurements were performed in a tube with 4.2 cm × 4.2 cm square cross

section. Assuming that plane waves propagate below the cut-off frequency of the tube (4200 Hz), the walls of the tube act as perfect mirrors to emulate a periodicity pattern in the

directions E1 and E2. The sample is placed at the end of the tube against a copper plug that closes the tube. A single microphone (1/4 inch pressure field B&K microphone type 4938)

attached on a one-dimensional robotised arm is used. This technique provides the experimental absorption coefficient at normal incidence without cross-calibration of many microphones and

with an enhanced accuracy at low frequencies21,22. Input sine signals were generated and output signals from microphone were acquired by the two-channel dynamic signal analyzer (Stanford

Research Systems model SR785). REFERENCES * MacDonald, E. & Wicker, R. Multiprocess 3d printing for increasing component functionality. _Science_ 353, aaf2093 (2016). Article  CAS 

Google Scholar  * Kadic, M., Bückmann, T., Stenger, N., Thiel, M. & Wegener, M. On the practicability of pentamode mechanical metamaterials. _Appl. Phys. Lett._ 100, 191901 (2012).

Article  ADS  Google Scholar  * Jiménez, N., Romero-García, V., Pagneux, V. & Groby, J.-P. Rainbow-trapping absorbers: Broadband, perfect and asymmetric sound absorption by subwavelength

panels for transmission problems. _Scientific Reports_ 7, 13595 (2017). Article  ADS  Google Scholar  * Shen, C., Díaz-Rubio, A., Li, J. & Cummer, S. A. A surface impedance-based

three-channel acoustic metasurface retroreflector. _Appl. Phys. Lett._ 112, 183503 (2018). Article  ADS  Google Scholar  * Affolderbach, C. _et al_. Study of additive manufactured microwave

cavities for pulsed optically pumped atomic clock applications. _Appl. Phys. Lett._ 112, 113502 (2018). Article  ADS  Google Scholar  * Vukusic, P. & Sambles, J. R. Photonic structures

in biology. _Nature_ 424, 852–855 (2003). Article  ADS  CAS  Google Scholar  * Miniaci, M., Krushynska, A., Movchan, A. B., Bosia, F. & Pugno, N. M. Spider web-inspired acoustic

metamaterials. _Appl. Phys. Lett._ 109, 071905 (2016). Article  ADS  Google Scholar  * Khalil, I. S. M., Dijkslag, H. C., Abelmann, L. & Misra, S. Magnetosperm: A microrobot that

navigates using weak magnetic fields. _Appl. Phys. Lett._ 104, 223701 (2014). Article  ADS  Google Scholar  * Oldham, D. J., Egan, C. A. & Cookson, R. D. Sustainable acoustic absorbers

from the biomass. _Appl. Acoust._ 72, 350–363 (2011). Article  Google Scholar  * Verdière, K., Panneton, R. & Elkoun, S. Prediction of the acoustic behavior of a parallel assembly of

hollow cylinders. _Appl. Acoust._ 102, 100–107 (2016). Article  Google Scholar  * Luu, H. T., Perrot, C., Monchiet, V. & Panneton, R. Three-dimensional reconstruction of a random fibrous

medium: Geometry, transport, and sound absorbing properties. _J. Acoust. Soc. Am._ 141, 4768–4780 (2017). Article  ADS  Google Scholar  * Romero-Garca, V., Theocharis, G., Richoux, O. &

Pagneux, V. Use of complex frequency plane to design broadband and sub-wavelength absorbers. _J. Acoust. Soc. Am._ 139, 3395–3403 (2016). Article  ADS  Google Scholar  * Johnson, D. L.,

Koplik, J. & Dashen, R. Theory of dynamic permeability and tortuosity in fluid-saturated porous media. _Journal of fluid mechanics_ 176, 379–402 (1987). Article  ADS  CAS  Google Scholar

  * Sanchez-Palencia, E. _Non-Homogeneous Media and Vibration Theory_, vol. 127 of _Lecture Notes in Physics_. (Springer-Verlag, Berlin, Heidelberg, 1980). * Auriault, J.-L., Boutin, C.

& Geindreau, C. _Homogenization of Coupled Phenomena in Heterogenous Media_. (ISTE Ltd and Wiley, 2009). * Lafarge, D., Lemarinier, P. & Allard, J. F. Dynamic compressibility of air

in porous structures at audible frequencies. _J. Acoust. Soc. Am._ 102, 1995–2006 (1997). Article  ADS  Google Scholar  * Zwikker, C. & Kosten, C. W. _Sound absorbing materials_.

(Elsevier Publishing Company, 1949). * Fang, N. _et al_. Ultrasonic metamaterials with negative modulus. _Nature materials_ 5, 452 (2006). Article  ADS  CAS  Google Scholar  * Boutin, C.

Acoustics of porous media with inner resonators. _J. Acoust. Soc. Am._ 134, 4717–4729 (2013). Article  ADS  Google Scholar  * Torrent, D. & Sánchez-Dehesa, J. Sound scattering by

anisotropic metafluids based on two-dimensional sonic crystals. _Phys_. _Rev_. _B_ 17 (2009). * Groby, J.-P., Huang, W., Lardeau, A. & Aurégan, Y. The use of slow waves to design simple

sound absorbing materials. _J. Appl. Phys._ 117, 124903 (2015). Article  ADS  Google Scholar  * Groby, J.-P., Pommier, R. & Aurégan, Y. Use of slow sound to design perfect and broadband

passive sound absorbing materials,. _J_. _Acoust_. _Soc_. _Am_. 139 (2016). * Jiménez, N., Huang, W., Romero-García, V., Pagneux, V. & Groby, J.-P. Ultra-thin metamaterial for perfect

and quasi-omnidirectional sound absorption. _Appl. Phys. Lett._ 109, 121902 (2016). Article  ADS  Google Scholar  * Jiménez, N., Romero-Garca, V., Pagneux, V. & Groby, J.-P. Quasiperfect

absorption by subwavelength acoustic panels in transmission using accumulation of resonances due to slow sound. _Phys. Rev. B_ 95, 014205 (2017). Article  ADS  Google Scholar  Download

references ACKNOWLEDGEMENTS This work was funded by the PAVNat project, RFI _Le Mans Acoustique_, Région Pays de la Loire. This article is based upon work from COST Action DENORMS CA15125,

supported by COST (European Cooperation in Science and Technology). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Laboratoire d’Acoustique de l’Université du Mans, LAUM - UMR CNRS 6613, Le

Mans Université, Avenue Olivier Messiaen, 72085, Le Mans Cedex 9, France W. Huang, L. Schwan, V. Romero-García, J.-M. Génevaux & J.-P. Groby Authors * W. Huang View author publications

You can also search for this author inPubMed Google Scholar * L. Schwan View author publications You can also search for this author inPubMed Google Scholar * V. Romero-García View author

publications You can also search for this author inPubMed Google Scholar * J.-M. Génevaux View author publications You can also search for this author inPubMed Google Scholar * J.-P. Groby

View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS J.P.G. conceived and designed the research. W.H. prepared the samples. W.H. and L.S.

performed the analytical and numerical calculations. W.H., L.S. and J.P.G. performed the experiments. All the authors contributed to the data analysis, discussion, and manuscript

preparation. CORRESPONDING AUTHOR Correspondence to L. Schwan. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE:

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a

Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit

to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are

included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and

your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this

license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Huang, W., Schwan, L., Romero-García, V. _et al._ 3D-printed sound

absorbing metafluid inspired by cereal straws. _Sci Rep_ 9, 8496 (2019). https://doi.org/10.1038/s41598-019-44891-z Download citation * Received: 13 February 2019 * Accepted: 28 May 2019 *

Published: 11 June 2019 * DOI: https://doi.org/10.1038/s41598-019-44891-z SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link

Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative