Analytic estimation of transition between instantaneous eigenstates of quantum two-level system

ABSTRACT Transition amplitudes between instantaneous eigenstates of a quantum two-level system are evaluated analytically on the basis of a new parametrization of its evolution operator,

which has recently been proposed to construct exact solutions. In particular, the condition under which the transitions are suppressed is examined analytically. It is shown that the analytic

expression of the transition amplitude enables us, not only to confirm the adiabatic theorem, but also to derive the necessary and sufficient condition for quantum two-level system to

remain in one of the instantaneous eigenstates. SIMILAR CONTENT BEING VIEWED BY OTHERS WIGNERIAN SYMPLECTIC COVARIANCE APPROACH TO THE INTERACTION-TIME PROBLEM Article Open access 28

December 2024 NUMBER OF STEADY STATES OF QUANTUM EVOLUTIONS Article Open access 22 June 2024 MAJORANA’S APPROACH TO NONADIABATIC TRANSITIONS VALIDATES THE ADIABATIC-IMPULSE APPROXIMATION

Article Open access 28 March 2023 INTRODUCTION A quantum system described by a time-dependent nondegenerate Hamiltonian _H_(_t_), such that \([H(t),\,H(t^{\prime} )]\ne 0\), does not possess

stationary states, since, in general, the mean value of an observable changes in time. The eigenstates of _H_(_t_) (instantaneous eigenstates) depend on time and evolve into those states

that are no longer the corresponding eigenstates of the Hamiltonian at that time instant. The deviations from the eigenstates, however, become negligible under the situation where the

so-called adiabatic theorem1,2,3 is applicable. The theorem states that the _n_th instantaneous eigenstate evolves remaining with continuity in the _n_th eigenstate at any time instant. The

condition for such an occurrence in a somewhat intuitive sense is that the quantum dynamics of the system is governed by a Hamiltonian that changes vanishingly slowly in time, yielding a

finite variation over an infinite time interval _T_ → ∞ (adiabatic limit). The adiabatic theorem plays an important role and constitutes a basis in a variety of research fields4,5,6,7,8,9.

In its proofs, the transitions to other instantaneous eigenstates over a finite time interval _T_ are estimated to be suppressed by 1/_T_ 2. The adiabatic theorem holds irrespectively of

details of the system under consideration, thus making it applicable to a wide class of quantum systems. On the other hand, any physically realizable process can not be in the adiabatic

limit because the time duration _T_ can not be made infinite and the physical process can be considered at most approximately adiabatic. It is therefore of practical relevance to understand

how well it is approximated as adiabatic and to estimate what the possible deviations from the adiabatic limit are. Notice that we are mainly concerned about the adiabaticity of quantum

state, that is, whether the quantum system remains in one of the instantaneous eigenstates for all times, when the time evolution can only be approximately adiabatic. There are classical

papers on these issues10,11, but the so-called Marzlin-Sanders inconsistency found in this century12 has provoked heated discussions13,14,15,16,17,18,19,20,21,22,23,24,25,26. Notice that the

theorem gives little information on these issues and a precise estimation of such deviations would require a knowledge of the exact dynamics. It is thus desirable to have an access to exact

solutions of the dynamics and then natural to expect to have new insights on these issues once a new strategy to construct analytical solutions has been proposed. In this respect, it is

worth while to stress that such a strategy for obtaining exact solutions for quantum two-level systems was proposed recently27,28,29 and actually several exactly solvable examples,

exploitable also for interacting qudits, have newly been obtained30,31,32,33,34 according to the strategy29. The purpose of this paper is twofold. First, the transition amplitudes between

instantaneous eigenstates of the general time-dependent Hamiltonian for quantum two-level system are expressed analytically in terms of appropriate quantities that parametrize the dynamics.

Second, the necessary and sufficient condition under which the transition from one of the instantaneous eigenstates to the other one is suppressed is derived and discussed. Two solvable

examples that can represent adiabatic processes are added to illustrate how such transition amplitudes behave as the time interval _T_ becomes large, confirming the adiabatic theorem and the

validity of the condition found here. TRANSITION AMPLITUDE BETWEEN INSTANTANEOUS EIGENSTATES Let a quantum two-level system be described by a time-dependent Hamiltonian

$$H(t)=(\begin{array}{cc}{\rm{\Omega }}(t) & \omega (t)\\ {\omega }^{\ast }(t) & -{\rm{\Omega }}(t)\end{array}),\,\omega (t)=|\omega (t)|{e}^{i{\varphi }_{\omega }(t)},$$ (1) where Ω

and _ω_ are time-dependent real and complex functions, respectively. The instantaneous eigenvalues \({E}_{\pm }(t)=\pm \sqrt{{{\rm{\Omega }}}^{2}(t)+{|\omega (t)|}^{2}}\) and eingenstates

\({|\pm \rangle }_{t}\), $${|+\rangle }_{t}=(\begin{array}{c}{e}^{\frac{i}{2}{\varphi }_{\omega }}\cos \,\frac{\theta }{2}\\ {e}^{-\frac{i}{2}{\varphi }_{\omega }}\sin \,\frac{\theta

}{2}\end{array}),\,{|-\rangle }_{t}=(\begin{array}{c}{e}^{\frac{i}{2}{\varphi }_{\omega }}\sin \,\frac{\theta }{2}\\ -\,{e}^{-\frac{i}{2}{\varphi }_{\omega }}\cos \,\frac{\theta

}{2}\end{array}),$$ (2) are both time dependent, where \(\tan \,\theta =|\omega |/{\rm{\Omega }}\). Here and in the following _t_-dependence will not be explicitly written and all quantities

are understood to be time dependent unless otherwise stated explicitly. According to the strategy proposed in29, the evolution operator _U_(_t_) is given by $$U=(\begin{array}{cc}a &

b\\ -{b}^{\ast } & {a}^{\ast }\end{array}),\,a=\,\cos \,\chi {e}^{-\frac{i}{2}({\rm{\Theta }}-{\varphi }_{\omega }+\varphi +{\varphi }_{\omega }(0))},\,b=-\,i\,\sin \,\chi

{e}^{-\frac{i}{2}({\rm{\Theta }}-{\varphi }_{\omega }-\varphi -{\varphi }_{\omega }(0))},$$ (3) where Θ is an arbitrary real-valued function of time with Θ(0) = 0 and $$\chi ={\int

}_{0}^{t}\,dt^{\prime} \frac{|\omega (t^{\prime} )|}{\hslash }\,\cos \,{\rm{\Theta }}(t^{\prime} ),$$ (4) $$\varphi ={\int }_{0}^{t}\,dt^{\prime} \frac{\mathrm{2|}\omega (t^{\prime}

)|}{\hslash }\,\frac{\sin \,{\rm{\Theta }}(t^{\prime} )}{\sin \,2\chi (t^{\prime} )}\mathrm{.}$$ (5) The function Ω, representing the longitudinal magnetic field in the case of spin 1/2, is

specified by $${\rm{\Omega }}=\frac{\hslash }{2}(\dot{{\rm{\Theta }}}-{\dot{\varphi }}_{\omega })+|\omega |\,\sin \,{\rm{\Theta }}\,\cot \,2\chi ,$$ (6) where dot (·) stands for derivative

w.r.t. time. The original idea of 29 is such that, if Ω is so adjusted to satisfy (6) for an arbitrarily given _ω_ and a parameter function Θ, then _U_ is explicitly given in terms of them

as in (3). One may, however, regard (3) as a _new parametrization_ of _U_. In fact, if the evolution operator _U_ is so parametrized by _χ_, Θ and _ϕ_ as in (3), the Eqs (4–6) are enough to

make _U_ satisfy the Schrödinger equation. The three parameters _χ_, Θ and _ϕ_ connect, though implicitly in general, the three parameters in the Hamiltonian Ω and \(\omega =|\omega

|{e}^{i{\varphi }_{\omega }}\) and those in the evolution operator _a_ and _b_ (|_a_|2 + |_b_2| = 1). It is stressed that this is nothing but a representation of the Schrödinger equation and

nothing has been imposed on the character of Ω and _ω_. It is not difficult to understand the meanings of the parameters introduced above. The parameter _χ_ parametrizes the transition

“angle,” while the others Θ and _ϕ_ their “phases,” see Eq. (3). It is convenient for the later use to rewrite the evolution operator _U_ in a compact form $$U=(\begin{array}{cc}\cos \,\chi

{e}^{-\frac{i}{2}({\rm{\Theta }}+\varphi -{\varphi }_{\omega }+{\varphi }_{\omega }(0))} & -i\,\sin \,\chi {e}^{-\frac{i}{2}({\rm{\Theta }}-\varphi -{\varphi }_{\omega }-{\varphi

}_{\omega }(0))}\\ -i\,\sin \,\chi {e}^{\frac{i}{2}({\rm{\Theta }}-\varphi -{\varphi }_{\omega }-{\varphi }_{\omega }(0))} & \cos \,\chi {e}^{\frac{i}{2}({\rm{\Theta }}+\varphi -{\varphi

}_{\omega }+{\varphi }_{\omega }(0))}\end{array})={e}^{\frac{i}{2}{\sigma }_{z}{\varphi }_{\omega }}{e}^{-i{\rm{\Phi }}{\boldsymbol{n}}\cdot {\boldsymbol{\sigma }}}{e}^{-\frac{i}{2}{\sigma

}_{z}{\varphi }_{\omega }(0)},$$ (7) where \({\boldsymbol{\sigma }}=({\sigma }_{x},\,{\sigma }_{y},\,{\sigma }_{z})\) is the Pauli matrix vector. We have introduced a unit vector

\({\boldsymbol{n}}=({n}_{x},\,{n}_{y},\,{n}_{z})\) with \({n}_{x}=\,\)\(\sin \,\xi \,\cos \,{\phi }_{-}=\frac{\sin \,\chi }{\sin \,{\rm{\Phi }}}\,\cos \,{\phi }_{-}\), \({n}_{y}=\,\sin \,\xi

\,\sin \,{\phi }_{-}=\frac{\sin \,\chi }{\sin \,{\rm{\Phi }}}\,\sin \,{\phi }_{-}\) and \({n}_{z}=\,\cos \,\xi =\frac{\cos \,\chi }{\sin \,{\rm{\Phi }}}\,\sin \,{\phi }_{+}\), and \(\cos

\,{\rm{\Phi }}=\,\cos \,\chi \,\cos \,{\phi }_{+}\), where angles are defined as \({\phi }_{\pm }=\frac{1}{2}({\rm{\Theta }}\pm \varphi )\). Then it is straightforward to calculate

transition amplitudes between instantaneous eigenstates. For example, the transition from the initial state \(|+{\rangle }_{0}\) to the other eigenstate \(|-{\rangle }_{t}\) occurs with an

amplitude (\({\theta }_{0}=\theta \mathrm{(0)}\)) $${}_{t}\langle \,-\,|U(t)|\,+\,{\rangle }_{0}=\,\cos \,\chi \,\cos \,{\phi }_{+}\,\sin \,\frac{\theta -{\theta }_{0}}{2}-\,\sin \,\chi

\,\sin \,{\phi }_{-}\,\cos \,\frac{\theta -{\theta }_{0}}{2}+i(\sin \,\chi \,\cos \,{\phi }_{-}\,\cos \,\frac{\theta +{\theta }_{0}}{2}-\,\cos \,\chi \,\sin \,{\phi }_{+}\,\sin

\,\frac{\theta +{\theta }_{0}}{2}).$$ (8) Similarly, the other amplitudes are concisely expressed in terms of trigonometric functions of _χ_, \({\phi }_{\pm }\) and _θ_35. Notice that these

expressions are exact and no approximation is involved. NECESSARY AND SUFFICIENT CONDITION FOR STAYING IN ONE OF THE INSTANTANEOUS EIGENSTATES AT ALL TIMES The analytical expression of

transition amplitude (8) enables us to investigate the condition under which no transition between different eigenstates at any time is allowed, \({}_{t}\langle -|U(t)|+\rangle

_{0}=\mathrm{0,}\,\,\forall t\ge 0\). The condition requires the following relations to hold $$\tan \,\frac{\theta +{\theta }_{0}}{2}=\,\tan \,\chi \frac{\cos \,{\phi }_{-}}{\sin \,{\phi

}_{+}},\,\tan \,\frac{\theta -{\theta }_{0}}{2}=\,\tan \,\chi \frac{\sin \,{\phi }_{-}}{\cos \,{\phi }_{+}}.$$ (9) They are combined to yield $$\tan \,\theta =\frac{2\,\tan \,\chi \,\cos

\,\varphi }{\sin \,{\rm{\Theta }}\,\cos \,\varphi \mathrm{(1}-{\tan }^{2}\chi )+\,\cos \,{\rm{\Theta }}\,\sin \,\varphi \mathrm{(1}+{\tan }^{2}\chi )}=\frac{|\omega |}{\hslash

}\frac{1}{y\,\cot \,2\chi +\frac{\dot{\chi }}{\sin \,2\chi }\,\tan \,\varphi },$$ (10) where _y_ is defined by $$y=\frac{|\omega |}{\hslash }\,\sin \,{\rm{\Theta }}.$$ (11) Notice that the

quantities in the Hamiltonian are then expressed, in terms of _y_, as $$|\omega |=\hslash \sqrt{{y}^{2}+{\dot{\chi }}^{2}},\,{\rm{\Omega }}=\frac{\hslash }{2}(\dot{{\rm{\Theta

}}}-{\dot{\varphi }}_{\omega })+\hslash y\,\cot \,2\chi ,$$ (12) while $$\tan \,{\rm{\Theta }}=\frac{y}{\dot{\chi }},\,\dot{\varphi }=\frac{2y}{\sin \,2\chi }.$$ (13) We obtain, from Eq.

(10), $${\dot{\varphi }}_{\omega }=\dot{{\rm{\Theta }}}-\frac{2\dot{\chi }}{\sin \,2\chi }\,\tan \,\varphi \mathrm{.}$$ (14) Equations (9) also yield $$\tan \,{\theta }_{0}=\frac{2\,\tan

\,\chi }{\tan \,{\rm{\Theta }}\,\cos \,\varphi \mathrm{(1}+{\tan }^{2}\chi )+\,\sin \,\varphi \mathrm{(1}-{\tan }^{2}\chi )},$$ (15) which can be reduced to the following differential

equation (assuming nonvanishing \(\tan \,{\theta }_{0}\ne 0\) without loss of generality) $$\frac{d}{dt}[\cos \,\chi (\sin \,\chi \,\sin \,\varphi +\frac{\cos \,\chi }{\tan \,{\theta

}_{0}})]=0.$$ (16) The solution is easily found to be \(\sin \,\varphi =\frac{\tan \,\chi }{\tan \,{\theta }_{0}}\), which leads to _θ_ = _θ_0 and \({\dot{\varphi }}_{\omega }=0\). Actually,

the differentiation of the solution w.r.t. _t_ yields \(y=\frac{\dot{\chi }\,\tan \,\chi }{\cos \,\varphi \,\tan \,{\theta }_{0}}\), resulting in \(|\omega |=\frac{\hslash \dot{\chi }}{\cos

\,\varphi }\) and \({\rm{\Omega }}=\frac{\hslash \dot{\chi }}{\cos \,\varphi \,\tan \,{\theta }_{0}}\). The result is consistent but trivial in the sense that the instantaneous eigenstates

do not at all evolve in time. In order to allow them to evolve, we need to admit to add a finite quantity which is not constant but whose velocity can be neglected. (This concept is in

accord with the notion of limit of adiabaticity, i.e., a finite change with an infinitesimal velocity). Let us introduce such a parameter _c_ and equate the quantity in the square

parentheses in (16) with \(\frac{1+c}{\tan \,{\theta }_{0}}\). Then the solution would be parametrized as $$\sin \,\varphi =\frac{\tan \,\chi }{\tan \,{\theta }_{0}}(1+\frac{c}{{\sin

}^{2}\chi }).$$ (17) The function _c_ (_c_(0) = 0) is assumed to be almost constant in time but takes a finite nonvanishing value at _t_ > 0, like in the case where _c_ is a function of

_t_/_T_ (0 ≤ _t_ ≤ _T_). We will neglect terms proportional to \(\dot{c}\propto \mathrm{1/}T\), but keep those proportional to \(\dot{\chi }\) or _c_. Differentiation of (17) w.r.t. _t_

gives $$y=\frac{\dot{\chi }\,\tan \,\chi }{\cos \,\varphi \,\tan \,{\theta }_{0}}(1-({\cot }^{2}\chi -1)c),$$ (18) which yields (see (12) and (14)) $${\rm{\Omega }}=\hslash \frac{\dot{\chi

}}{\cos \,\varphi }\frac{1+2c}{\tan \,{\theta }_{0}},$$ (19) $$\omega =\hslash \frac{\dot{\chi }}{\cos \,\varphi }\sqrt{1-\frac{4c(1+c)}{{\tan }^{2}{\theta }_{0}}}{e}^{i{\varphi }_{\omega

}},\,{\dot{\varphi }}_{\omega }\sim 0.$$ (20) The consistency condition \(\tan \,\theta =|\omega |/{\rm{\Omega }}\) requires that $$c=\frac{1}{2}(\frac{\cos \,\theta }{\cos \,{\theta

}_{0}}-1).$$ (21) Thus we have found that the condition that no transition between different eigenstates occurs requires that the Hamiltonian has to be parametrized as above with arbitrary

functions \(\chi ,{\varphi }_{\omega }\) and _c_. The condition \(|\dot{\chi }|\gg |\dot{c}| \sim 0\) is equivalent to \(\dot{\theta } \sim 0\), implying, together with \({\varphi }_{\omega

} \sim 0\), that the instantaneous eigenstates have to vary infinitesimally slowly in time (_necessity_), though the Hamiltonian itself can vary at a finite rate26. It is interesting to see

that Eq. (19) can actually be integrated, thus assuring that such a parametrization is always possible, to yield $$\tan \,\varphi =\frac{\cos \,{\theta }_{0}}{\sin (2\zeta )}(\frac{\tan

\,{\theta }_{0}}{\tan \,\theta }-\,\cos (2\zeta )),$$ (22) where \(\zeta =\frac{1}{\hslash }{\int }_{0}^{t}\,ds\sqrt{{{\rm{\Omega }}}^{2}(s)+|\omega (s{)|}^{2}}\). This, together with (17),

results in the specification of _χ_ in terms of Ω and |_ω_|. It is also possible to show that when the Hamiltonian is characterized by the above Ω and _ω_, (19) and (20), the transition

amplitude (8) vanishes, provided \(\dot{c} \sim 0\), i.e., \(\dot{\theta } \sim 0\) (_sufficiency_). (In order to keep the relation (17) intact, we would need a correction term proportional

to \(\dot{c}\) in _y_, \(\dot{c}{(\cos \varphi \tan {\theta }_{0})}^{-1}\), which was neglected in (18)). EXAMPLES As an example, we may consider a particular case of physical interest.

Choose the functions _χ_ and _y_ as $$\tan \,\chi =\,\sin \,\alpha t,\,y={\nu }_{0}\,\sin \,\alpha t$$ (23) with parameters \({\nu }_{0} > 0\) and \(\alpha \propto \mathrm{1/}T\). Then we

have $$|\omega |=\hslash \sqrt{{\nu }_{0}^{2}{\sin }^{2}\alpha t+{(\frac{\alpha \cos \alpha t}{1+{\sin }^{2}\alpha t})}^{2}},$$ (24) $${\rm{\Omega }}=\frac{\hslash }{2}(\dot{{\rm{\Theta

}}}-{\dot{\varphi }}_{\omega })+\frac{\hslash {\nu }_{0}}{2}{\cos }^{2}\alpha t,$$ (25) where \(\tan \,{\rm{\Theta }}=\frac{{\nu }_{0}}{\alpha }\mathrm{(1}+{\sin }^{2}\alpha t)\tan \,\alpha

t\). Observe that the physical system under consideration could be well approximated for small \(\alpha ,\,{\dot{\varphi }}_{\omega } \sim 0\) by $$|\omega |\sim \hslash {\nu }_{0}|\sin

\,\alpha t|,\,{\rm{\Omega }}\sim \frac{\hslash {\nu }_{0}}{2}{\cos }^{2}\alpha t$$ (26) except for the initial transient times, where we have $$|\omega (0)|=\hslash \alpha ,\,{\rm{\Omega

}}(0)=\hslash {\nu }_{0}.$$ (27) By setting \(\alpha T=\frac{\pi }{2}\), we are going to consider a physical process where the magnetic field (for spin \(\frac{1}{2}\) case), starting from

an approximately longitudinal one (27) if \(\alpha =\frac{\pi }{2T}\ll {\nu }_{0}\), varies slowly in time characterized by the trigonometric functions (26), reaching an approximately

transversal one $$|\omega (T)|=\hslash {\nu }_{0},\,{\rm{\Omega }}(T)=\frac{\hslash }{2}(\frac{{\alpha }^{2}}{2{\nu }_{0}}-{\dot{\varphi }}_{\omega }(T))\ll \hslash {\nu }_{0}.$$ (28)

Clearly the adiabaticity of the process is characterized by the inequalities $$\frac{\alpha }{{\nu }_{0}}=\frac{\pi }{2T{\nu }_{0}}\ll 1,\,\frac{{\dot{\varphi }}_{\omega }}{{\nu }_{0}}\ll

1.$$ (29) Observe that in this case the parameter _ν_0 can be viewed as a characteristic frequency relevant to the energy of the system, while _α_ is the fundamental frequency governing the

variation of the Hamiltonian. Since we are given an analytical expression for every quantity (for example, \(\varphi (t)=\frac{{\nu }_{0}}{4\alpha }\mathrm{(6}\alpha t-\,\sin \,2\alpha

t)\)), the transition amplitudes and probabilities are calculated without any approximation. The figures in Fig. 1 show the behaviour of transition probability \({|}_{t}{\langle

-|U(t)|+\rangle }_{0}{|}^{2}\) as a function of time _t_ for several values of \({\nu }_{0}T\), together with that of longitudinal (Ω) and transversal (|_ω_|) magnetic fields. It is evident

that in the large \({\nu }_{0}T\gg 1\) limit, the transition probability becomes vanishingly small. In the above example, the Hamiltonian itself varies infinitesimally slowly, realizing a

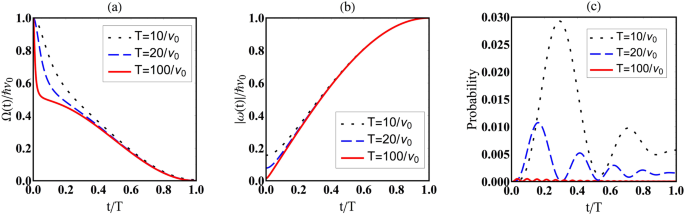
process where the instantaneous eigenstates do not make transitions. We may consider another example that realizes the same situation even if the Hamiltonian varies with a nonvanishing rate.

For example, we may choose such a _χ_ that realizes \(\varphi ={\nu }_{0}t\) with a finite parameter _ν_0 and \(c=-\,\frac{1}{2}(\frac{t}{T}{)}^{3}\) according to (17) and \({\varphi

}_{\omega }=0\), which means that the speed of variation of _χ_ is essentially _ν_0, a finite value irrelevant to _T_, while the other parameter _c_ varies slowly in time with \(\dot{c}\)

proportional to 1/_T_. In this case, as Eqs (19) and (20) show, the characteristic frequency of the magnetic field (i.e., Hamiltonian) is _ν_0, while its instantaneous eigenstates become

slowly varying for large _T_. The persistence of oscillations in Ω and _E_ (Fig. 2(a,c)) even for large _T_ and its absence in _θ_ (Fig. 2(b)) are manifestations of these statements. The

transition probability tends to vanish for large _T_ (Fig. 2(d)) even if the Hamiltonian and its eigenvalues vary with finite speeds ((a) and (c)). This fact confirms that no transitions

between instantaneous eigenstates are allowed for large _T_ even for such a varying Hamiltonian. Our approach allows us to exhibit an example in which the system stays in its instantaneous

eigenstate, even though the Hamiltonian varies with a nonvanishing rate. SUMMARY AND DISCUSSIONS In summary, the adiabatic theorem is confirmed on the basis of the explicit expressions of

the transition amplitudes (see (8) and also refer to35), which are derived from the new parametrization of the evolution operator for the quantum two-level system29. What is stressed here is

that these expressions enable us to evaluate such transition amplitudes directly in any physical situation, from the adiabatic to diabatic cases. Furthermore, we have made it clear that the

necessary and sufficient condition that the state prepared initially in one of the eigenstates of the Hamiltonian remains in the corresponding instantaneous eigenstate at any time is that

_the speed of variation of the eigenstate is negligible_, i.e., $$\dot{\theta }\sim 0,\,{\dot{\varphi }}_{\omega }\sim 0,$$ (30) compared with the frequency (i.e., energy \(/\hslash \)) of

the system. Notice that this condition, though mentioned in26, has never been explicitly derived so far. It is different from the traditional one \(\hslash {|}_{t}{\langle -|\dot{H}|+\rangle

}_{t}|/({E}_{-}(t)-{E}_{+}(t{))}^{2}\ll 1\) and is free from the insufficiency found for the latter12,13. Actually the traditional condition is read in the case of two-level systems as

\(\hslash \sqrt{{(\frac{1}{2}\dot{\theta })}^{2}+{(\frac{1}{2}{\dot{\varphi }}_{\omega }\sin \theta )}^{2}}\) \(\ll {E}_{+}-{E}_{-}=2\sqrt{{{\rm{\Omega }}}^{2}+|\omega {|}^{2}}\)and

therefore even if this condition is satisfied, a resonant transition with \(\hslash |{\dot{\varphi }}_{\omega }|={E}_{+}-{E}_{-}\ne 0\) can occur between eigenstates when the magnetic field

is almost longitudinal \(0 < |\,\sin \,\theta |\ll 1\). Needless to say, such situations are not allowed according to the conditions (30) because one of them is not satisfied \(\hslash

|{\dot{\varphi }}_{\omega }|\ll /{E}_{+}-{E}_{-}\). It is remarked here that the conditions (30) actually follow from \(\dot{\theta }\,\sin \,\theta \sim 0\) under the assumption of

nonvanishing factor \(\sin \,\theta \ne 0\). When this factor becomes vanishingly small at all times, no further conditions are required for other quantities25, but this is a trivial case

where the magnetic field always points to the _z_-direction, a case described by a diagonal Hamiltonian. Notice also that there is an exceptional situation. If the Hamiltonian itself becomes

vanishingly small \({\rm{\Omega }}\sim 0,\,|\omega |\sim 0\), the above condition will loose its meaning and our approach can say nothing about the adiabaticity of state36. Remember that it

is generally difficult to eliminate potential loopholes in the discussions on and proposals of the adiabatic condition because we are hardly able to reach the exact dynamics except for some

limited cases, even for simple quantum two-level systems. It is stressed in this respect that our conclusion is derived from the analytic parametrization of the exact dynamics of the

two-level system and offers a definite answer, with its range of validity specified, to this issue for the quantum two-level systems. Further applications to other fundamental issues,

including, e.g., the Landau–Zener transition4,5, will be published elsewhere. DATA AVAILABILITY STATEMENT All data generated or analysed during this study are included in this article.

REFERENCES * Born, M. & Fock, V. Proof of adiabatic law. _Z. Phys._ 51, 165–180 (1928). Article  ADS  CAS  Google Scholar  * Kato, T. On the Adiabatic Theorem of Quantum Mechanics. _J.

Phys. Soc. Jpn._ 5, 435 (1950). Article  ADS  Google Scholar  * Messiah, A. _Quantum Mechanics_ (Amsterdam, 1962). * Landau, L. D. Zur theorie der energieubertragung. II. _Phys. Z.

Sowjetunion_ 2, 46–51 (1932). CAS  MATH  Google Scholar  * Zener, C. Non-adiabatic crossing of energy levels. _Proc. R. Soc. A_ 137, 696–702 (1932). Article  ADS  Google Scholar  *

Gell-Mann, M. & Low, F. Bound states in quantum field theory. _Phys. Rev._ 84, 350–354 (1951). Article  ADS  MathSciNet  CAS  Google Scholar  * Berry, M. V. Quantal phase factors

accompanying adiabatic changes. _Proc. R. Soc. A_ 392, 45–57 (1984). Article  ADS  MathSciNet  Google Scholar  * Farhi, E. _et al_. A quantum adiabatic evolution algorithm applied to random

instances of an NP-complete problem. _Science_ 291, 472–476 (2001). Article  ADS  MathSciNet  Google Scholar  * Facchi, P. & Pascazio, S. Quantum Zeno subspaces. _Phys. Rev. Lett._ 89,

080401 (2002). Article  ADS  MathSciNet  CAS  Google Scholar  * Crisp, M. D. Adiabatic-following approximation. _Phys. Rev. A_ 8, 2128–2135 (1973). Article  ADS  Google Scholar  * Davis, J.

P. & Pechukas, P. Nonadiabatic transitions induced by a time-dependent Hamiltonian in semicalssical adiabatic limit–2-sate case. _J. Chem. Phys._ 64, 3129–3138 (1976). Article  ADS  CAS

  Google Scholar  * Marzlin, K.-P. & Sanders, B. C. Inconsistency in the application of the adiabatic theorem. _Phys. Rev. Lett._ 93, 160408 (2004). Article  ADS  Google Scholar  * Tong,

D. M., Singh, K., Kwek, L. C. & Oh, C. H. Quantitative conditions do not guarantee the validity of the adiabatic approximation. _Phys. Rev. Lett._ 95, 110407 (2005). Article  ADS  CAS 

Google Scholar  * Tong, D. M., Singh, K., Kwek, L. C. & Oh, C. H. Sufficiency criterion for the validity of the adiabatic approximation. _Phys. Rev. Lett._ 98, 15042 (2007). Google

Scholar  * MacKenzie, R., Morin-Duchesne, A., Paquette, H. & Pinel, J. Validity of the adiabatic approximation in quantum mechanics. _Phys. Rev. A_ 76, 044102 (2007). Article  ADS 

Google Scholar  * Rigolin, G., Ortiz, G. & Ponce, V. H. Beyond the quantum adiabatic approximation: Adiabatic perturbation theory. _Phys. Rev. A_ 78, 052508 (2008). Article  ADS  Google

Scholar  * Amin, M. H. S. Consistency of the adiabatic theorem. _Phys. Rev. Lett._ 102, 220401 (2109). Article  MathSciNet  Google Scholar  * Comparat, D. General conditions for quantum

adiabatic evolution. _Phys. Rev. A_ 80, 012106 (2009). Article  ADS  MathSciNet  Google Scholar  * Tong, D. M. Quantitative condition is necessary in guaranteeing the validity of the

adiabatic approximation. _Phys. Rev. Lett._ 104, 120401 (2010). Article  ADS  CAS  Google Scholar  * Zhao, M. & Wu, J. Comment on “Quantitative condition is necessary in guaranteeing the

validity of the adiabatic approximation”. _Phys. Rev. Lett._ 106, 138901 (2011). Article  ADS  Google Scholar  * Comparat, D. Comment on “Quantitative condition is necessary in guaranteeing

the validity of the adiabatic approximation”. _Phys. Rev. Lett._ 106, 138902 (2011). Article  ADS  Google Scholar  * Tong, D. M. Tong replies. _Phys. Rev. Lett._ 106, 138903 (2011). Article

  ADS  Google Scholar  * Ortigoso, J. Quantum adiabatic theorem in light of the Marzlin-Sanders inconsistency. _Phys. Rev. A_ 86, 032121 (2012). Article  ADS  Google Scholar  * Li, D.

Invalidity of the quantitative adiabatic condition and general conditions for adiabatic approximations. _Laser Phys. Lett._ 13, 055203 (2016). Article  ADS  Google Scholar  * Du, J. _et al_.

Experimental study of the validity of quantitative conditions in the quantum adiabatic theorem. _Phys. Rev. Lett._ 101, 060403 (2008). Article  ADS  Google Scholar  * Wang, Z.-Y. &

Plenio, M. B. Necessary and sufficient condition for quantum adiabatic evolution by unitary control fields. _Phys. Rev. A_ 93, 052107 (2016). Article  ADS  Google Scholar  * Barnes, E. &

Das Sarma, S. Analytically solvable driven time-dependent two-level quantum systems. _Phys. Rev. Lett._ 109, 060401 (2012). Article  ADS  Google Scholar  * Barnes, E. Analytically solvable

two-level quantum systems and Landau-Zener interferometry. _Phys. Rev. A_ 88, 013818 (2013). Article  ADS  Google Scholar  * Messina, A. & Nakazato, H. Analytically solvable Hamiltonians

for quantum two-level systems and their dynamics. _J. Phys. A: Math. Theor._ 47, 445302 (2014). Article  ADS  MathSciNet  Google Scholar  * Grimaudo, R., Messina, A. & Nakazato, H.

Exactly solvable time-dependent models of two interacting two-level systems. _Phys. Rev. A_ 94, 022108 (2016). Article  ADS  Google Scholar  * Grimaudo, R., Messina, A., Ivanov, P. A. &

Vitanov, N. V. Spin-1/2 sub-dynamics nested in the quantum dynamics of two coupled qutrits. _J. Phys. A: Math. Theor._ 50, 175301 (2017). Article  ADS  MathSciNet  Google Scholar  *

Markovich, L. A., Grimaudo, R., Messina, A. & Nakazato, H. An example of interplay between Physics and Mathematics: Exact resolution of a new class of Riccati Equations. _Ann. Phys._

385, 522–531 (2017). Article  ADS  MathSciNet  CAS  Google Scholar  * Grimaudo, R., Belousov, Y., Nakazato, H. & Messina, A. Time evolution of a pair of distinguishable interacting spins

subjected to controllable and noisy magnetic fields. _Ann. Phys._ 392, 242–259 (2018). Article  ADS  MathSciNet  CAS  Google Scholar  * Grimaudo, R., de Castro, A. S. M., Nakazato, H. &

Messina, A. Classes of exactly solvable generalized semi-classical Rabi Systems. Preprint at, https://arxiv.org/abs/1803.02086 to appear in _Ann. der Phys_ (2018) * Suzuki, T. Graduation

Thesis. (Waseda University, 2018, in Japanese). * Xu, K. _et al_. Breaking the quantum adiabatic speed-limit by jumping along geodesics. Preprint at, https://arxiv.org/abs/1711.02911 (2017).

Download references AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Physics, Waseda University, Tokyo, 169-8555, Japan Takayuki Suzuki & Hiromichi Nakazato * Dipartimento di

Fisica e Chimica dell’Universitá di Palermo, Via Archirafi, 36, I-90123, Palermo, Italy Roberto Grimaudo * INFN, Sezione di Catania, Catania, Italy Roberto Grimaudo & Antonino Messina *

Dipartimento di Matematica ed Informatica dell’Universita di Palermo, Via Archirafi 34, I-90123, Palermo, Italy Antonino Messina Authors * Takayuki Suzuki View author publications You can

also search for this author inPubMed Google Scholar * Hiromichi Nakazato View author publications You can also search for this author inPubMed Google Scholar * Roberto Grimaudo View author

publications You can also search for this author inPubMed Google Scholar * Antonino Messina View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS

H.N. wrote the main manuscript text and T.S. prepared Figures 1 and 2. A.M. and R.G., as well as T.S., reviewed the manuscript. CORRESPONDING AUTHOR Correspondence to Hiromichi Nakazato.

ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE: Springer Nature remains neutral with regard to jurisdictional

claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which

permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to

the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless

indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or

exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints

and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Suzuki, T., Nakazato, H., Grimaudo, R. _et al._ Analytic estimation of transition between instantaneous eigenstates of quantum two-level

system. _Sci Rep_ 8, 17433 (2018). https://doi.org/10.1038/s41598-018-35741-5 Download citation * Received: 31 May 2018 * Accepted: 11 November 2018 * Published: 27 November 2018 * DOI:

https://doi.org/10.1038/s41598-018-35741-5 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative KEYWORDS * Instantaneous Eigenstates * Adiabatic Theorem * Exact

Dynamics * Pauli Matrix Vector * Construct Analytical Solutions