Effect of correlations in swarms on collective response

ABSTRACT Social interaction increases significantly the performance of a wide range of cooperative systems. However, evidence that natural swarms limit the number of interactions suggests

potentially detrimental consequences of excessive interaction. Using a canonical model of collective motion, we find that the collective response to a dynamic localized

perturbation–emulating a predator attack–is hindered when the number of interacting neighbors exceeds a certain threshold. Specifically, the effectiveness in avoiding the predator is

enhanced by large integrated correlations, which are known to peak at a given level of interagent interaction. From the network-theoretic perspective, we uncover the same interplay between

number of connections and effectiveness in group-level response for two distinct decision-making models of distributed consensus operating over a range of static networks. The effect of the

number of connections on the collective response critically depends on the dynamics of the perturbation. While adding more connections improves the response to slow perturbations, the

opposite is true for fast ones. These results have far-reaching implications for the design of artificial swarms or interaction networks. SIMILAR CONTENT BEING VIEWED BY OTHERS TRANSITION

FROM SIMPLE TO COMPLEX CONTAGION IN COLLECTIVE DECISION-MAKING Article Open access 17 March 2022 COLLECTIVE DYNAMICS OF SWARMALATORS WITH HIGHER-ORDER INTERACTIONS Article Open access 21

February 2024 NATURAL SWARMS IN 3.99 DIMENSIONS Article Open access 24 April 2023 INTRODUCTION Social interaction is critical for swarms to perform an effective and coordinated response to

changing environments. Social activity and the associated transmission of information through the interaction network have recently attracted considerable attention in a wide range of

complex systems: from the biological realm–flock of birds1, 2, school of fish3,4,5,6, swarm of insects7,8,9, and human crowds10–to social networks11, and artificial multi-agent systems such

as the power grid12, 13 or robotic swarms14, 15. The characteristics of the interaction network are known to strongly affect the swarm dynamics16,17,18 and, in particular, its capacity to

respond to local perturbations4, 6, 19, 20. Increasing the number of interactions between agents usually improves the performance of the collective, but it is known that most natural swarms

operate with a limited number of connections. For instance, flocking starlings interact on average with 6 to 7 conspecifics21 and swarms of midges8 regulate their nearest-neighbor distance

depending on the size of the swarm. Gordon _et al_.22 have shown that one species of ants (_L_. _fuliginosus_) regulate its rate of social encounters following: _(i)_ changes in the nestmate

density for undisturbed ant colonies, and _(ii)_ the introduction of an external perturbation–workers from another colony–in the colony. This limited interaction appears to be a behavioral

feature and not a direct result of physical limitations of their sensing capabilities. These findings suggest that natural swarms may tune the amount of interaction or number of connections

in order to increase their capacity to collectively respond to environmental changes. Classic phenomenological models of collective motion feature a critical point at a certain number of

connections that maximizes the integrated correlation in the swarm23. The observed collective dynamics of midges8 provides experimental evidence that this swarm tunes the amount of

interaction–inferred from density–in a way that maximizes correlations. This critical behavior may help explain why different social organisms seem to self-limit the number of connections,

assuming that large integrated correlations do enhance the collective response for the benefit of biological functions such as predator avoidance or foraging. From the theoretical

standpoint, some models of decision-making dynamics predict that over-reliance on social information can render a collective unresponsive to changing circumstances24, 25. Models of consensus

in mobile communicating agents have also shown that consensus can be reached more efficiently with a limited interaction range26. Several empirical studies19, 27, 28 have shown that for

social behaviors such as the adoption of new ideas or innovations to spread successfully over a network, agents must be exposed to multiple reinforcements coming from a minimum fraction of

their connections. This behavioral spreading process is called _complex contagion_, in contrast with simple contagion processes such as the spread of information or diseases. It is now well

known that these complex contagion processes are very sensitive to the topology of the network connecting agents. In particular, studies of complex contagion modeling the adoption of new

behaviors29, 30 have shown that, in some contexts, adding connections decreases the spread of adoption. Understanding the consequences of excessive connections is critical for achieving new

functional predictions on collective animal behavior3, 4, and for the study of spreading of behaviors in networked systems such as online communities. From a technological viewpoint,

developing a predictive theoretical framework to understand under which circumstances these effects appear is of paramount importance for the emerging field of large-scale swarm robotics14,

15. Here, we investigate the relationship between the number of interacting agents and the responsiveness of the collective. First, we present an analysis of response to a predator attack

using a classical model of collective motion in which self-propelled particles (SPPs) move by adjusting their direction of travel to that of their neighbors. We find that the capacity of the

agents to avoid the predator is directly related to the integrated correlation of the collective, and thus peaks at a finite number of connections. Second, we extend the study beyond swarm

dynamics by considering a general distributed decision-making model. We measure how the properties of the interaction network affect the dynamics of the collective decision when facing

external influences. Finally, we develop an analytical framework based on linear time-invariant (LTI) theory that allows us to establish how the connectivity of a networked multi-agent

system affects its overall responsiveness. This framework may be used to determine policies on interaction regulation for optimal dynamical response to a given perturbation. RESULTS

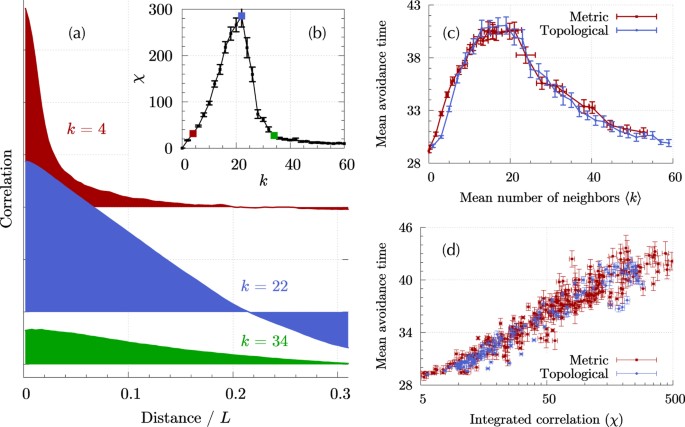
COLLECTIVE RESPONSE TO A PREDATOR ATTACK A natural starting point to characterize the responsiveness of the collective motion is to study the connected correlation in fluctuations of the

velocity9. We follow the framework developed by Attanasi _et al_.7, 8 and compute the connected correlation in velocity fluctuations _C_(_r_) (Eq. (6)) for a swarm composed of _N_ = 2,048

SPPs while varying the number of neighbors _k_. In order to investigate the behavior of swarms displaying a high degree of alignment, we perform the calculations in the low noise regime (see

Methods). The integrated correlation _χ_ (Eq. (7)) is a measure of the total amount of correlation present in the system7. In the collective behavior literature, this quantity is commonly

referred to as _susceptibility_ in reference to its analog in equilibrium statistical physics, where the dissipation-fluctuation theorem establishes that the response of the system is

proportional to this quantity. We find that a collective of SPPs following the Vicsek model in the ordered phase can exhibit a large integrated correlation if the number of neighbors _k_ is

set to an appropriate level (Fig. 1(b)). The integrated correlation depends both on the span of correlations (how far in space the behavior of one agent influences another) and the intensity

of correlations (how strong this influence is)7, and there is an intrinsic trade-off between them: an increase in the number of neighbors allows the information to travel farther through

the network–increased correlation length–but causes each agent to be exposed to more information, thus decreasing the relevance of each individual signal–decreased correlation strength. The

correlation function is shown in Fig. 1(a) for three different values of the number of neighbors _k_, illustrating this trade-off. For small values of _k_ (e.g. _k_ = 4 in Fig. 1(a)),

correlations are large but confined to short distances. As _k_ increases, so does the spread of correlations and thus _χ_. Above a certain optimal number of neighbors, which is approximately

\({k}^{\ast }\simeq 20\) for the particular configuration used in our calculation, the increase in spatial spread cannot compensate the reduction in correlation strength and _χ_ diminishes

with increasing number of neighbors. In order to illustrate how a highly aligned swarm benefits from a large _χ_, we have performed a model simulation of a predator attacking a group of SPPs

following the Vicsek consensus and measured the survival rate of agents with different number of connections (see Methods). The emergent collective avoidance maneuver is shown in Fig. 2 for

three selected snapshots of a predator attack and in movies M1–M3 (see Supplementary Note I). At _t_ 0 (leftmost frame), the predator starts the attack on a highly-aligned section of the

swarm. Only the agents that detect the predator–those inside the red disk–react according to Eq. (8). After 13 iterations, agents outside the detection area are collectively reacting to the

threat thanks to the social information transmitted through the swarm. After 26 iterations from the start of the attack, all agents in the vicinity of the predator perform a global evasive

maneuver. Notice that the information transfer has taken place strikingly fast, which is in good agreement with recent empirical observations of collective turns in flocks of starlings1 and

startled schools of fish5, 31. It is worth pointing out that animals avoid predators using behaviors and strategies considerably more sophisticated than the model presented here. For

instance, Rosenthal _et al_.31 have shown how schooling golden shiner fish use visual cues such as a fast change in speed to signal to other members the necessity to flee. However, this

idealized model illustrates how classical concepts from statistical mechanics such as the connected correlation can be linked to aspects of a collective’s behavior crucial for the survival

of its members. A similar case could be made for the capacity of swarms to forage for food, achieve optimal pattern formation, or other examples of animal collective behavior where a timely

response to perturbations is critical32, 33. The characteristic avoidance time for the swarm, defined as the average time elapsed between two consecutive catches by the predator, is shown in

Fig. 1(c) as a function of the mean number of neighbors for both metric and topological interactions. In the latter case, the mean is exactly the imposed outdegree value _k_, while in the

former the average is computed over all agents and iterations. Interestingly, both interactions yield essentially the same outcome. Starting from a noninteracting collective (〈_k_〉 = 0), the

avoidance time grows with the number of neighbors up to a maximum value about 40% larger than the noninteracting time. From that optimal point at approximately 20 neighbors, the avoidance

time monotonously decreases with increasing _k_, down to the value obtained for a noninteracting collective. The variations in the mean avoidance time are not due to variations in the mode

but to the appearance of a heavy tail in the distribution of times (see Supplementary Note II). In order to better illustrate the effect of the number of connections in predator avoidance,

Movies M1 to M3 in the Supplemental Information present the movement of the swarm for each of the three characteristic regimes: optimal _k_ = 16, insufficient _k_ = 4, and excessive _k_ = 40

respectively. Figure 1(d) shows a clear and systematic improvement of the swarm’s collective predator avoidance with increased _χ_. Taking the avoidance time as a measure of the capacity of

a swarm to respond to localized perturbations, these simulations show that large correlations can translate into enhanced group-level responses beneficial to the swarm. INFLUENCE OF

CONNECTIVITY ON COLLECTIVE DECISION-MAKING The SPP model considered here is inarguably one of the simplest models of collective motion where the agents choose their heading in order to

achieve a consensus in a distributed fashion. Despite its simplicity, the model features a rich phenomenology–from its critical behavior to its coupling of the dynamics _of_ the interaction

network with the dynamics _on_ the network–that has been exhaustively documented in the literature. In order to abstract the effects of the collective decision-making process from the

dynamics of the agents and the statistical description of the swarm, we turn our attention to a minimalist description of decision-making dynamics involving a set of fixed agents interacting

through a static network and performing a distributed consensus protocol. An archetypical minimalist model of decision-making is the so-called linear threshold model34, 35, which is a

generalization of the simple majority vote model36. Using this model with different degrees of modularity, Nematzadeh _et al_.37 revealed that the network structure has a strong influence on

the diffusion process. A similar conclusion was obtained by Centola19 using experiments on a specifically designed social network. In both cases, the effectiveness in diffusion was

characterized by the influence of perturbations onto the asymptotic global state. Here, we use the same model as Nematzadeh _et al_.37 to study the responsiveness of a decision-making

process to perturbations. We characterize this response capacity using the polarization speed _c_, which is essentially the rate at which agents adapt their individual state to an induced

perturbation detected only by a minority of informed agents (see Methods). These informed agents can be considered as “leaders” that drive the system from _P_ = 0 to _P_ = 1, much like the

SPPs detecting the predator lead the swarm to perform a collective evasive maneuver or initiators can drive sheep herds to specific targets38. The polarization speed is shown in Fig. 3 for

two extreme kinds of network wiring: a fixed-outdegree random directed network where each agent is randomly connected with _k_ agents, and an undirected regular one-dimensional lattice (a

ring) where each agent is connected with its _k_ nearest neighbors. With both wirings, the polarization speed _c_ is maximum for a finite outdegree _k_ * which, for large systems, is fairly

independent of the total number of agents _N_ (see Supplementary Note III). We have chosen a large enough number of informed leaders to guarantee that the system eventually reaches _P_ = 1,

i.e. a full polarization, in a finite time. This way, the polarization speed is determined by the short-time response capacity of the system, and not its asymptotic polarization at long

times (for different ratios of informed leaders, see Supplementary Note IV). How fast the system reaches full polarization depends on the degree of the network and, as seen for the SPPs, too

many connections hinder the performance of the system. The results in Fig. 3 also reveal that the structure of the network can enhance or diminish the effects of connectivity on the

response capacity. While the optimal outdegree _k_ * = 10 is the same for completely random and highly structured networks, the polarization speed in the random network shows a larger

sensitivity to the amount of connections. These results do not exhaustively prove the existence of such an optimal outdegree for any arbitrary topology. Nonetheless, it is reasonable to

assume that most realistic examples of complex networked systems possess a network structure somewhere in between the two extreme cases considered here39 (see Supplementary Note V). A

systematic study of the polarization speed for a wider collection of complex networks may reveal how the short-time response of a system is related to other properties of the interaction

network such as degree distribution, average shortest connecting path, and clustering coefficient40. RESPONSIVENESS OF COOPERATIVE MULTI-AGENT SYSTEMS In the previous sections, we have

stressed the importance of distributed consensus problems in both biological and social systems. Both the SPP and the majority vote models provide excellent phenomenological frameworks to

study how the level of connectivity among agents affects the responsiveness of cooperative systems. However, their phenomenological nature limits our ability to identify and characterize the

underlying mechanisms responsible for the impaired collective responses under excessive connectivity. Consensus and cooperation in networked multi-agent systems is a topic that is starting

to receive significant attention in control theory and distributed computing owing to numerous possible engineering applications41. For instance, the power grid, urban traffic, arrays of

distributed sensors, multi-robot systems, and social networks are some examples of collective systems requiring an effective response to local perturbations. The design of such

systems–especially in the emerging field of swarm robotics–can be optimized using a theoretical framework that highlights the underlying mechanism and predicts under which conditions the

detrimental effect of excessive connectivity will manifest. The LTI system theory provides one of the most elementary candidates for such a framework. We consider a set of _N_ + 1 agents

performing a linear consensus protocol, and model the effects of local perturbations by setting one agent as a “leader” that does not participate to the local consensus dynamics albeit

influencing agents connected to it. The leader-follower distributed linear consensus protocol presented in Eq. (11) is fairly standard16,17,18, 41,42,43, and can be used to analyze the

capacity of the system to follow and adapt to fast changes in the behavior of the leading agent (see Methods). To simplify the problem as much as possible, static and undirected regular

one-dimensional lattice topologies–_k_ nearest neighbors with a ring topology–are considered for the network of interaction between agents. Significant attention has been dedicated to the

problem of convergence to consensus18 and controllability of multi-agent dynamics44 in the presence of complex network topologies–possibly switching–with directed or undirected information

flow41. Here, given the simple topology of the static network, both convergence to consensus and controllability are guaranteed. Instead, our focus lies with the overall responsiveness of

the collective in adapting to fast changes in the dynamics of the single leader–in control-theoretic terms, the input. To characterize the effects of varying levels of connectivity on the

far-from-consensus responsiveness of the collective, Fig. 4 shows the response capacity of this system to oscillations of the leading agent as a function of the number of connections _k_,

and for input oscillation frequencies _ω_ spanning four orders of magnitude. This response capacity, measured by the total amplitude gain (see Methods), can be roughly interpreted as the

number of agents that are capable of following the perturbation induced by the leader. For such a rudimentary linear system, the response capacity exhibits a surprisingly rich structure. At

low frequencies \(\omega \ll {\omega }_{0}\), more connections always translates into an improvement in the system’s capacity to respond to perturbations. At high frequencies \(\omega

\gtrsim {\omega }_{0}\), the opposite is true: adding connections yields a systematic reduction in the system’s performance. A very interesting intermediate frequency regime is also observed

(e.g. \(\omega \sim 0.01{\omega }_{0}\) in Fig. 4), where the responsiveness features a peak at a finite number of connections. The inset highlights that, in this intermediate frequency

regime, the system can essentially double the amount of agents capable of following the leader by tuning the outdegree to its optimal value. This trend is reminiscent of what we have

uncovered for the dependency of the correlations (Fig. 1(b)), mean avoidance time (Fig. 1(c)), and polarization speed (Fig. 3) with _k_ in the previous phenomenological models. Using the

analytical expression for the gain, we can obtain general predictions for the responsiveness on arbitrary networks in the limits of low and high frequencies. For instance, in the limit of

low frequencies, any system with an undirected interaction network (for directed ones, see Supplementary Note VI) will respond to perturbations of frequency \(\omega \ll {\omega }_{0}\) as

$${H}_{\omega \ll {\omega }_{0}}^{2}={\Vert {{\bf{H}}}_{0}\Vert }^{2}-{\omega }^{2}{{\bf{H}}}_{0}^{\dagger }{{\bf{W}}}^{-2}{{\bf{H}}}_{0}+O({\omega }^{4}),$$ (1) where H 0 = H(0) = W −1 W

_l_ is the gain at _ω_ = 0, W is related to the inter-agent connectivity, and W _l_ to the connectivity of the agents to the leader (see Methods). For any connected network, H 0 is a vector

with all components equal to 145, and thus Eq. (1) can be written as $${H}_{\omega \ll {\omega }_{0}}^{2}=N-{\omega }^{2}\sum _{i,j}{({{\bf{W}}}^{-2})}_{ij}+O({\omega }^{4}\mathrm{)}.$$ (2)

At high frequency, the gain is $${H}_{\omega \gg {\omega }_{0}}^{2}={\omega }^{-2}{\Vert {{\bf{W}}}_{l}\Vert }^{2}+O({\omega }^{-4}\mathrm{)}.$$ (3) Note that the low-frequency limit is

fully determined by the connectivity between agents W, while the high-frequency limit only depends on the connectivity of the agents with the leader W _l_ . For networks with a fixed

outdegree _k_, the norm of this connectivity decreases as \({\Vert {{\bf{W}}}_{l}\Vert }^{2} \sim \mathrm{1/}k\). Thus, at high frequencies, distributed consensus systems have a decrease in

responsiveness with increasing number of connections. This is a general behavior and not a particular feature of the regular ring network used in the previous calculations. In general, there

is no such direct relation between W −2 and the amount of connections in the network, which means that the behavior of the system at low frequencies is more sensitive to the features of the

interaction network beyond its outdegree distribution. From the standpoint of designing artificial swarms, this analysis highlights that the pace of typical perturbations faced by the

system is central in defining appropriate levels of interagent connectivity. When subjected to slow-changing perturbations, the system’s effectiveness always benefits from a higher level of

connectivity. Comparing with earlier observations, one can deduce that in the low-frequency regime, the system does not require high correlation strengths for good propagation of the signal,

but it does benefit from an increase in speed that higher correlation lengths provide. On the other hand, fast perturbations inevitably reduce the system’s effectiveness with increasing

interagent connectivity. Extending the comparison, this suggests that in the high-frequency regime, a high correlation strength is paramount for the signal to be effectively transmitted

throughout the entire system. DISCUSSION A myriad of organisms manifest swarming and social organization to some degree. It is well known that such collective behaviors notably improve the

effectiveness of fundamental tasks, e.g. predator avoidance, foraging, or mating. However, our phenomenological and analytical study of different models of collective behavior reveals that

an excess in social interaction can have detrimental effects, in that it leads to a reduced capacity of response to fast, localized perturbations. Specifically, we have shown that for a

system of self-propelled agents–subjected to a consensus protocol to align their velocities–the capacity for collective predator avoidance is maximized when the number of connections is

limited to the value corresponding to the peak in correlations. Beyond the field of swarming, we have found that in simulations of a minimalist model of collective decision-making–the linear

threshold model–the speed at which the effects of a perturbation spread through the system is reduced if the outdegree is increased above a certain value. Lastly, a frequency-domain

analysis within the LTI framework reveals the underlying cause of this phenomenology: in general, adding more connections in a multi-agent system increases its responsiveness to slow

perturbations while decreasing its responsiveness to fast ones. Simulations of an idealized predator attack upon a swarm of SPPs following the Vicsek model with both metric and topological

interactions reveal a direct correspondence between the amount of correlations in the swarm and the survivability of its members in hostile environments. This correspondence is reminiscent

of the fluctuation-dissipation theorem for equilibrium statistical physics, that relates the integrated correlation of the system to the real susceptibility. Since in this model the

integrated correlation peaks at a given number of connections, the link with predator avoidance observed here shows that tuning the number of connections allows the group to increase its

responsiveness and enhance its performance in biologically-relevant functions while maintaining a high degree of alignment. We speculate that this may be the reason behind the apparently

self-imposed limit on social activity observed in flocking birds21, social ants22, and other taxa (see Supplementary Note VII). In terms of correlations, an increase in the number of

neighbors yields an increase in the correlation length at the cost of decreasing the correlation strength. At low number of connections (e.g. below _k_ = 20 in Fig. 1(b)) this is a

beneficial trade-off for the swarm: the increase in correlation length effectively allows the information to propagate faster through the interaction network. Thus, more agents are capable

of responding to the presence of the threat. However, at higher numbers (e.g. beyond _k_ = 20 in Fig. 1(b)), the increase in correlation length only affects agents far away from any danger

and marginally benefits the overall performance of the swarm. On the other hand, this increase in the correlation length is accompanied by a drastic reduction in correlation strength that,

in turn, severely reduces the responsiveness of agents in the vicinity of the threat. An alternative approach to understand the effect of the level of interagent interaction on collective

response is to perform a network-theoretic analysis of the system of SPPs. As the agents move and align their heading with that of their neighbors, they form a dynamic network of

interactions17. These interaction networks are temporal, homogeneous, small-world networks17 with a topology–degree distribution, shortest path, clustering coefficient, etc.–strongly

dependent on the number of interacting neighbors _k_, which in turn influences the group’s dynamics18. The spreading of the fleeing behavior through the SPP interaction network in the

presence of a predator parallels the complex contagion processes studied in social networks where, as mentioned, the topology of the underlying network profoundly influences the

effectiveness of contagion. For this reason, studying simplified models of decision-making and distributed consensus over different static networks provides valuable insights into how the

responsiveness of collective motion is affected by the properties of the interaction. The number of neighbors has similar effects on responsiveness for the case of multi-agent systems

performing distributed consensus with a threshold-triggered dynamics, meaning that an agent only changes its state when a certain ratio of its neighbors do. These kind of threshold events

have been observed in the spread of behavior over social networks19, 27, 28 and the so-called flash expansion of whirligig beetles facing a potential predator threat46. It is worth pointing

out that our results for dynamical responsiveness complement previous studies associated with global properties such as the robustness of the interaction network16 or the consensus speed18.

In these studies, increasing the amount of interaction eventually yields diminishing returns–i.e. less gain per neighbor–but never an actual reduction in the property of interest.

Diminishing returns can only justify the preference for a finite number of connections if the cost for establishing links between agents is significant. However, quantifying such costs in

biological swarms is close to impossible given the complexity associated with sensory and neurological requirements16, 18. In contrast, the present study on the dynamical responsiveness of

the swarm shows an absolute reduction in swarming effectiveness when the number of neighbors is increased above a certain level. This fact raises the important question of why collectives

with excessive connectivity display a reduced effectiveness under some scenarios such as a predator attack, but not under others such as consensus reaching. The present analysis of the

responsiveness of multi-agent systems following LTI consensus dynamics under time-varying perturbations reveals that one key element for predicting the effect of connectivity on

responsiveness is the speed of perturbation changes. In many cases, being able to react efficiently to perturbations in the appropriate time scale is essential for the performance of systems

conducting distributed consensus. For example, ants performing collective transport of food rely on transiently informed peers to locate their nest32. These informed “leaders” forget their

knowledge after a time of joining the collective action, and thus provide a changing signal with a certain characteristic time scale to the swarm. Successful transport depends both on a high

consensus over the direction of movement and a proper responsiveness to this dynamic input. As can be seen in Fig. 4, high levels of connectivity provide marginal benefits when the system

is subjected to slow perturbations, but yield a sizable reduction in effectiveness in the presence of relatively fast perturbations. In summary, previous studies in the animal realm8, 21, 22

and in social systems19 provide evidence suggesting that, in some cases, it is optimal for collectives to limit the amount of interaction. We have presented simulations of predator

avoidance under the SPP model for collective motion, a numerical study of decision-making dynamics, and an analysis of the frequency-response in a consensus protocol that consistently

exhibit a decreased responsiveness associated with an excess of connections or interaction. Given that these models are relatively general and unadorned, we suggest that this non-trivial

relation between responsiveness and connectivity may be a general feature of a wide range of complex systems involving distributed consensus. Besides shedding a new light on our

understanding of collective behavior, this has also clear implications for the design of networked systems. Even ignoring the possible costs of establishing connections and transmitting

information between agents, it may be desirable to limit the number of connections in order to achieve a more effective dynamical response. METHODS SELF-PROPELLED PARTICLES We use the

self-propelled particles (SPP) model developed by Vicsek _et al_.23 as a minimalist model of collective motion that captures the cooperative alignment of orientation. There are several

extensions and improvements to this model that generate more realistic and specific dynamics47, but we use the original model for the sake of generality and simplicity. Each particle moves

in a two-dimensional periodic space and changes its direction of motion at discrete timesteps in order to align to its neighbors’ mean orientation according to

$$\begin{array}{rcl}{{\bf{x}}}_{i}(t+{\rm{\Delta }}t) & = & {{\bf{x}}}_{i}(t)+{\rm{\Delta }}t\,{{\bf{v}}}_{i}(t),\\ {\theta }_{i}(t+{\rm{\Delta }}t) & = & {\rm{\arg }}(\sum

_{j \sim i}{{\bf{v}}}_{j}(t))+2\pi {\eta }_{i}(t),\end{array}$$ (4) where the velocity vector \({{\bf{v}}}_{i}={v}_{0}{\hat{{\boldsymbol{\theta }}}}_{i}\) has constant magnitude _v_ 0 and

direction _θ_ _i_ , arg() gives the orientation of a vector, and _η_ _i_ (_t_) is a random number uniformly distributed in the [−_η_/2,_η_/2] range. The sum _j_ ~ _i_ is performed over the

neighbors of _i_ (including _i_ itself). While the original Vicsek model considers that a pair of agents interact–i.e., are neighbors–if they are closer than a certain distance (metric

interaction), there is strong evidence that certain natural systems such as flocks of birds interact with a fixed number of neighbors instead (topological or metric-free interaction)21, 48.

For this reason, we have studied different kinds of interactions only to find the same phenomenology; the responsiveness depends essentially on the amount of interaction in the swarm, not

the details of the interaction rule itself. The results presented in this work have been obtained by computing the dynamics of a set of _N_ = 2,048 SPPs following the Vicsek model starting

from random positions and velocity orientations. The numerical calculations have been performed using the libspp library49. Further implementation details can be found in Supplementary Note 

III. CORRELATIONS The dimensionless velocity fluctuation is defined as $$\delta {{\boldsymbol{\phi }}}_{i}=\frac{{{\bf{v}}}_{i}-\langle {\bf{v}}\rangle }{\sqrt{\sum _{k=1}^{N}{\Vert

{{\bf{v}}}_{k}-\langle {\bf{v}}\rangle \Vert }^{2}/N}},$$ (5) where \(\langle {\bf{v}}\rangle ={\sum }_{i=1}^{N}{{\bf{v}}}_{i}/N\) is the average velocity. The connected correlation function

is then given by $$C(r)=\frac{{\sum }_{i\ne j}\delta {{\boldsymbol{\phi }}}_{i}\cdot \delta {{\boldsymbol{\phi }}}_{j}\delta (r-{r}_{ij})}{{\sum }_{i\ne j}\delta (r-{r}_{ij})},$$ (6) where

\({r}_{ij}=\Vert {{\bf{r}}}_{i}-{{\bf{r}}}_{j}\Vert \) is the distance between agents _i_ and _j_, and _δ_(_r_) the Dirac delta distribution. For finite-size systems, one can use the maximum

of the cumulative correlation as an estimation of the total correlation in the system7, $$\chi \equiv \mathop{{\rm{\max }}}\limits_{{r}_{0}}({\int }_{r < {r}_{0}}C(r)d{\bf{r}}).$$ (7)

This integrated correlation is usually referred to as susceptibility. While in collective animal behavior one cannot formally relate this integrated correlation to the response of the

system, several studies7, 50 have shown a phenomenological relation between _χ_ defined as Eq. (7) and the way the group responds collectively to a perturbation. To obtain numerical values

of the correlation function _C_ and _χ_, we compute the histogram of the correlations in the system every 5 × 103 iterations during 2 × 106 iterations, after discarding the first 5 × 104

iterations as transient dynamics. The correlation _C_(_r_) shown in Fig. 1(a) is the average over 400 histograms obtained with this procedure. PREDATOR ATTACK The predator is introduced as

an agent that does not participate in the consensus protocol. Instead, it is afforded predatory capabilities: it moves 40% faster than swarming agents, systematically in the direction

pointing to the closest one. When the predator “catches” an agent, the latter is removed from the simulation. An agent can only detect the presence of the threat when it is located at a

distance smaller than a fixed “danger-detection” radius _R_ _D_ ; as soon as the agent detects it, an evasive maneuver is initiated with the agent moving away in the direction opposite to

the predator. We have set _R_ _D_ to be constant throughout the simulations and independent of the number of neighbors. The fleeing behavior takes precedence over the collective motion of a

particular agent for as long as the predator lies inside its danger-detection area. Thus, the agents in this simulation follow the equations of motion (4) with the exception that

$${{\bf{v}}}_{i}(t)={v}_{0}\frac{{{\bf{x}}}_{i}(t)-{{\bf{x}}}_{P}(t)}{\Vert {{\bf{x}}}_{i}(t)-{{\bf{x}}}_{P}(t)\Vert }\quad {\rm{if}}\quad \Vert {{\bf{x}}}_{i}(t)-{{\bf{x}}}_{P}(t)\Vert <

{R}_{D},$$ (8) where X _P_ denotes the predator’s position. The mean avoidance time shown in Fig. 1(c,d) is obtained by computing the swarm dynamics in the presence of a single predator

(introduced after a transient of 2,000 iterations) for 500 different runs of 5,000 iterations each. The reason for computing several runs instead of running the calculation for longer times

is that the results depend on the density of agents in the swarm, and the repeated removal of agents by the predator can cause significant changes in the density after long times. COLLECTIVE

DECISION-MAKING The linear threshold model is a generalization of the simple majority vote model36 where the state of each agent or node _i_ is determined by a binary variable _s_ _i_  = 

{0, 1}. The dynamics of the model dictates that, at a given timestep _t_, _s_ _i_ (_t_) takes the value 0 or 1 according to $${s}_{i}(t+\mathrm{1)}=\{\begin{array}{ll}1 &

{\rm{if}}{\langle {s}_{j}(t)\rangle }_{j \sim i} > \theta \\ 0 & \text{otherwise},\end{array}$$ (9) where \({\langle \cdot \rangle }_{j \sim i}\) is the average over all neighbors of

_i_ and _θ_ is a parameter that determines the minimum ratio of neighbors that need to be in the state _s_ = 1 for an agent to switch to it. To study the effects of a perturbation on the

collective decision-making process, we consider the following scenario: a given set of _N_ = 2,048 networked agents reside in the “ground” state _s_ _i_  = 0 ∀_i_ when, at _t_ = 0, an

unspecified perturbation induces a small fraction of “informed” agents to abruptly switch to (and remain in) the state _s_ {_j_} = 1. This change propagates through the network and causes

more agents to switch from state 0 to 1. If the fraction of initially informed agents is large enough and the network is connected, the mean polarization _P_(_t_) = 〈_s_ _i_ (_t_)〉 will

eventually reach _P_ = 1. One can characterize the responsiveness of the decision-making process by the speed at which this change propagates through the system, measured by the rate of

change in polarization, $$c=\frac{dP}{dt}=\frac{1}{N}\frac{d}{dt}\sum _{i=1}^{N}{s}_{i}(t).$$ (10) Further details can be found in Supplementary Notes III–V. DISTRIBUTED CONSENSUS IN

MULTI-AGENT SYSTEMS Let us consider a group of _N_ + 1 identical agents performing a distributed consensus protocol on their scalar state-variable _x_ _i_ (_t_), through a connected and

undirected network. The system is characterized by the global state vector X(_t_) = {_x_ _i_ (_t_); _i_ = 0, …, _N_} and the adjacency matrix of the underlying graph A = {_a_ _ij_ ; _i_, _j_

 = 0, …, _N_}, where _a_ _ij_  = 1 if agent _i_ is connected to _j_ and 0 otherwise. Given a certain connectivity graph, the state of the system evolves according to

$$\begin{array}{rcl}\frac{d{x}_{i}}{dt} & = & \frac{{\omega }_{0}}{{k}_{i}}\sum _{j=0}^{N}{a}_{ij}({x}_{j}(t)-{x}_{i}(t)),\\ & = & \sum

_{j=0}^{N}{w}_{ij}{x}_{j}(t),\end{array}$$ (11) where _ω_ 0 is the natural response frequency of our identical agents, and \({k}_{i}={\sum }_{j=0}^{N}{a}_{ij}\) is the degree of agent _i_,

i.e. its number of neighbors in the network sense. The quantity _w_ _ij_  = _ω_ 0(_a_ _ij_ /_k_ _i_  − _δ_ _ij_ ) is introduced for the sake of a compact notation for the governing dynamical

equations. As is classical with many swarming systems, these dynamics involve relative output information of neighboring agents41. We model the process of distributed transfer of

information by considering a leader-follower consensus dynamics. This is implemented by affording one agent–say agent _i_ = 0–with a dynamics not abiding by Eq. (11), but instead following

an arbitrary trajectory _x_ 0(_t_) = _u_(_t_). This single control input has a direct effect onto the dynamics of its _k_ 0 neighboring agents, but also indirect effects onto the dynamics of

many more agents through the coupled set of dynamical equations (11). In the presence of this single leader, Eq. (11) can be recast as $$\frac{d{x}_{i}}{dt}=\sum

_{j=1}^{N}{w}_{ij}{x}_{j}(t)+{w}_{i0}u(t),$$ (12) for _i_ = 1, …, _N_. Despite the static nature of the topology of interaction, this leader-follower consensus model is a good idealization

of the process of social information transfer occurring in startled schools of fish or flocks of birds, where one individual has access to privileged information about a potential threat or

other kind of external perturbation. This temporary leader triggers a wave of agitation that propagates strikingly fast through the swarm5, 51. Such waves of agitation are initiated by

extremely rapid changes in the leading agent’s state, which very effectively propagate to all other swarming agents1. Within this leader-follower scheme, one can characterize the

responsiveness of the multi-agent system undergoing the distributed consensus process as its capacity to follow fast changes in the leader’s dynamics, _u_(_t_). Specifically, with an input

signal oscillating at the frequency _ω_, _u_(_t_) = _u_ 0 _e_ _iωt_, the state of all agents at long times becomes proportional to _u_(_t_) with a factor given by the transfer function,

$${\bf{H}}(\omega )=\mathop{\mathrm{lim}}\limits_{t\to \infty }\frac{{\bf{X}}(t)}{u(t)}={(i\omega {\bf{I}}-{\bf{W}})}^{-1}{{\bf{W}}}_{l}.$$ (13) where I is the identity matrix of dimension

_N_, W = {_w_ _ij_ } is the _N_ × _N_ consensus protocol matrix and W _l_  = {_w_ _i_0} is the _N_-vector resulting from projecting W onto the subspace of the leader. This allows us to

define the system’s responsiveness as the norm of this transfer function, or gain, \({H}^{2}={\Vert {\bf{H}}\Vert }^{2}={\sum }_{i}{|{h}_{i}(\omega )|}^{2}\), with |_h_ _i_ (_ω_)| ≤ 1 for

all _i_ and _ω_ 52. As is clear from Eq. (13), the gain has a nontrivial dependency on the topology of the agents’ connectivity, including that of the leading agent, through the entries of W

and W _l_ . REFERENCES * Attanasi, A. _et al_. Information transfer and behavioural inertia in starling flocks. _Nature Phys._ 10, 691–696 (2014). Article  ADS  CAS  Google Scholar  * Mora,

T. _et al_. Local equilibrium in bird flocks. _Nature Physics_ ADVANCE ONLINE PUBLICATION, doi:10.1038/nphys3846 (2016). * Sumpter, D., Buhl, J., Biro, D. & Couzin, I. Information

transfer in moving animal groups. _Theory Biosci._ 127, 177–186 (2008). Article  PubMed  Google Scholar  * Strandburg-Peshkin, A. _et al_. Visual sensory networks and effective information

transfer in animal groups. _Curr. Biol._ 23, R709–R711 (2013). Article  CAS  PubMed  PubMed Central  Google Scholar  * Herbert-Read, J. E., Buhl, J., Hu, F., Ward, A. J. W. & Sumpter, D.

J. T. Initiation and spread of escape waves within animal groups. _R. Soc. Open Sci._ 2, 140355 (2015). Article  PubMed  PubMed Central  Google Scholar  * Calovi, D. S. _et al_. Collective

response to perturbations in a data-driven fish school model. _J. R. Soc. Interface_ 12, 20141362 (2015). Article  PubMed  PubMed Central  Google Scholar  * Attanasi, A. _et al_. Collective

behaviour without collective order in wild swarms of midges. _PLoS Comput. Biol._ 10, e1003697 (2014). Article  PubMed  PubMed Central  Google Scholar  * Attanasi, A. _et al_. Finite-size

scaling as a way to probe near-criticality in natural swarms. _Phys. Rev. Lett._ 113, 238102 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Ni, R., Puckett, J. G., Dufresne, E. R.

& Ouellette, N. T. Intrinsic fluctuations and driven response of insect swarms. _Phys. Rev. Lett._ 115, 118104, doi:10.1103/PhysRevLett.115.118104 (2015). Article  ADS  PubMed  Google

Scholar  * Moussad, M., Perozo, N., Garnier, S., Helbing, D. & Theraulaz, G. The walking behaviour of pedestrian social groups and its impact on crowd dynamics. _PLoS ONE_ 5, e10047

(2010). Article  ADS  Google Scholar  * Fowler, J. H. & Christakis, N. A. Cooperative behavior cascades in human social networks. _Proc. Natl. Acad. Sci. USA_ 107, 5334–5338 (2010).

Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Alizadeh, M., Li, X., Wang, Z., Scaglione, A. & Melton, R. Demand-side management in the smart grid: Information processing

for the power switch. _IEEE Signal Processing Magazine_ 29, 55–67, doi:10.1109/MSP.2012.2192951 (2012). Article  ADS  Google Scholar  * Weckx, S., D’Hulst, R., Claessens, B. & Driesen,

J. Multiagent charging of electric vehicles respecting distribution transformer loading and voltage limits. _IEEE Trans_. _Smart Grid_ 5, 2857–2867, doi:10.1109/TSG.2014.2345886 (2014).

Article  Google Scholar  * Rubenstein, M., Cornejo, A. & Nagpal, R. Programmable self-assembly in a thousand-robot swarm. _Science_ 345, 795–799 (2014). Article  ADS  CAS  PubMed  Google

Scholar  * Kawashima, H. & Egerstedt, M. Manipulability of leaderfollower networks with the rigid-link approximation. _Automatica_ 50, 695–706, doi:10.1016/j.automatica.2013.11.041

(2014). Article  MathSciNet  MATH  Google Scholar  * Young, G. F., Scardovi, L., Cavagna, A., Giardina, I. & Leonard, N. E. Starling flock networks manage uncertainty in consensus at low

cost. _PLoS Comput. Biol._ 9, e1002894 (2013). Article  ADS  MathSciNet  CAS  PubMed  PubMed Central  Google Scholar  * Komareji, M. & Bouffanais, R. Resilience and controllability of

dynamic collective behaviors. _PLoS ONE_ 8, e82578, doi:10.1371/journal.pone.0082578 (2013). Article  ADS  PubMed  PubMed Central  Google Scholar  * Shang, Y. & Bouffanais, R. Influence

of the number of topologically interacting neighbors on swarm dynamics. _Sci. Rep._ 4, 4184 (2014). Article  ADS  PubMed  PubMed Central  Google Scholar  * Centola, D. The spread of behavior

in an online social network experiment. _Science_ 329, 1194–1197, doi:10.1126/science.1185231 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Bassett, D. S., Alderson, D. L. &

Carlson, J. M. Collective decision dynamics in the presence of external drivers. _Phys. Rev. E_ 86, 036105, doi:10.1103/PhysRevE.86.036105 (2012). Article  ADS  Google Scholar  * Ballerini,

M. _et al_. Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study. _Proc. Natl. Acad. Sci. USA_ 105, 1232–1237 (2008).

Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Gordon, D. M., Paul, R. E. & Thorpe, K. What is the function of encounter patterns in ant colonies? _Anim. Behav._ 45,

1083–1100 (1993). Article  Google Scholar  * Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I. & Shochet, O. Novel type of phase-transition in a system of self-driven particles. _Phys.

Rev. Lett._ 75, 1226–1229 (1995). Article  ADS  MathSciNet  CAS  PubMed  Google Scholar  * Torney, C. J., Lorenzi, T., Couzin, I. D. & Levin, S. A. Social information use and the

evolution of unresponsiveness in collective systems. _J_. _R_. _Soc_. _Interface_ 12, doi:10.1098/rsif.2014.0893 (2014). * Kao, A. B. & Couzin, I. D. Decision accuracy in complex

environments is often maximized by small group sizes. _Proc. R. Soc. B_ 281, 20133305 (2014). Article  PubMed  PubMed Central  Google Scholar  * Baronchelli, A. & Díaz-Guilera, A.

Consensus in networks of mobile communicating agents. _Phys_. _Rev_. _E_ 016113 (2012). * Karsai, M., Iñiguez, G., Kaski, K. & Kertész, J. Complex contagion process in spreading of

online innovation. _Journal of The Royal Society Interface_ 11, doi:10.1098/rsif.2014.0694 (2014). * Hodas, N. O. & Lerman, K. The simple rules of social contagion. _Scientific reports_

4, 4343 (2014). Article  ADS  PubMed  PubMed Central  Google Scholar  * Centola, D. & Macy, M. Complex contagions and the weakness of long ties. _American Journal of Sociology_ 113,

702–734, doi:10.1086/521848 (2007). Article  Google Scholar  * Siegel, D. A. Social networks and collective action. _American Journal of Political Science_ 53, 122–138,

doi:10.1111/j.1540-5907.2008.00361.x (2009). Article  Google Scholar  * Rosenthal, S. B., Twomey, C. R., Hartnett, A. T., Wu, H. S. & Couzin, I. D. Revealing the hidden networks of

interaction in mobile animal groups allows prediction of complex behavioral contagion. _Proceedings of the National Academy of Sciences_ 112, 4690–4695, doi:10.1073/pnas.1420068112,

http://www.pnas.org/content/112/15/4690.abstract (2015) Article  ADS  CAS  Google Scholar  * Gelblum, A. _et al_. Ant groups optimally amplify the effect of transiently informed individuals.

_Nature Communications_ 6, 7729, doi:10.1038/ncomms8729. (2015). Article  CAS  PubMed  PubMed Central  Google Scholar  * Krause, J. & Ruxton, G. D. _Living in Groups_. Oxford Series in

Ecology and Evolution (Oxford University Press, Oxford, U.K., 2002). * Granovetter, M. Threshold models of collective behavior. _American Journal of Sociology_ 83, 1420–1443

http://www.jstor.org/stable/2778111 (1978) Article  Google Scholar  * Granovetter, M. & Soong, R. Threshold models of diffusion and collective behavior. _The Journal of Mathematical

Sociology_ 9, 165–179, doi:10.1080/0022250X.1983.9989941 (1983). Article  MATH  Google Scholar  * Aldana, M. & Larralde, H. Phase transitions in scale-free neural networks: Departure

from the standard mean-field universality class. _Phys. Rev. E_ 70, 066130, doi:10.1103/PhysRevE.70.066130 (2004). Article  ADS  Google Scholar  * Nematzadeh, A., Ferrara, E., Flammini, A.

& Ahn, Y.-Y. Optimal network modularity for information diffusion. _Phys. Rev. Lett._ 113, 088701, doi:10.1103/PhysRevLett.113.088701 (2014). Article  ADS  PubMed  Google Scholar  *

Toulet, S., Gautrais, J., Bon, R. & Peruani, F. Imitation combined with a characteristic stimulus duration results in robust collective decision-making. _PLoS ONE_ 10, 1–16,

doi:10.1371/journal.pone.0140188 (2015). Article  Google Scholar  * Watts, D. J. & Strogatz, S. H. Collective dynamics of “small-world” networks. _Nature_ 393, 440–442 (1998). Article 

ADS  CAS  PubMed  MATH  Google Scholar  * Sekunda, A., Komareji, M. & Bouffanais, R. Interplay between signaling network design and swarm dynamics. _Network Science_ 4, 244–265 (2016).

Article  Google Scholar  * Olfati-Saber, R., Fax, J. A. & Murray, R. M. Consensus and cooperation in networked multi-agent systems. _Proc. IEEE_ 95, 215–233 (2007). Article  Google

Scholar  * Jadbabaie, A., Lin, J. & Morse, A. S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. _IEEE Trans. Autom. Contr._ 48, 988–1001 (2003). Article

  MathSciNet  MATH  Google Scholar  * Shang, Y. & Bouffanais, R. Consensus reaching in swarms ruled by a hybrid metric-topological distance. _Europ. Phys. J. B_ 87, 294 (2014). Article 

ADS  MathSciNet  Google Scholar  * Komareji, M. & Bouffanais, R. Controllability of a swarm of topologically interacting autonomous agents. _Int. J. Complex Systems in Science_ 3, 11–19

(2013). Google Scholar  * Jadbabaie, A., Lin, J. & Morse, A. S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. _IEEE Transactions on Automatic Control_

48, 988–1001, doi:10.1109/TAC.2003.812781 (2003). Article  MathSciNet  MATH  Google Scholar  * Romey, W. L. & Lamb, A. R. Flash expansion threshold in whirligig swarms. _PLoS ONE_ 10,

1–12, doi:10.1371/journal.pone.0136467 (2015). Article  Google Scholar  * Vicsek, T. & Zafeiris, A. Collective motion. _Phys. Rep._ 517, 71–140 (2012). Article  ADS  Google Scholar  *

Ginelli, F. & Chaté, H. Relevance of metric-free interactions in flocking phenomena. _Phys. Rev. Lett._ 105, 168103 (2010). Article  ADS  PubMed  Google Scholar  * Mateo, D.

Swarming-spp: A C++ library for simulations of self-propelled particles and the theoretical study of emergent swarming behaviors, doi:10.5281/zenodo.30587 (2015). * Cavagna, A. _et al_.

Scale-free correlations in starling flocks. _Proc. Natl. Acad. Sci. USA_ 107, 11865–11870 (2010). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Hemelrijk, C. K. &

Hildenbrandt, H. Scale-free correlations, influential neighbours and speed control in flocks of birds. _J. Stat. Phys._ 158, 563–578 (2015). Article  ADS  MathSciNet  MATH  Google Scholar  *

Ogata, K. _Modern Control Engineering_, fifth edn. (Prentice Hall, Upper Saddle River, NJ, 2010). Download references ACKNOWLEDGEMENTS This work was supported by a grant from the Temasek

Lab (TL@SUTD) under the STARS project (D.M.) and a grant #SMIG14006 from the Singapore–MIT Alliance for Research and Technology (SMART) (R.B.). The authors thank Nikolaj Sørensen for

fruitful discussions on state-space modeling and Dr. Mardavij Roozbehani for his input on the importance of nodal dynamics for the time-constrained controllability of a system. AUTHOR

INFORMATION AUTHORS AND AFFILIATIONS * Singapore University of Technology and Design, 8 Somapah Road, Singapore, 487372, Singapore David Mateo, Yoke Kong Kuan & Roland Bouffanais Authors

* David Mateo View author publications You can also search for this author inPubMed Google Scholar * Yoke Kong Kuan View author publications You can also search for this author inPubMed 

Google Scholar * Roland Bouffanais View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS D.M. and R.B. designed the study. D.M. performed

research, developed the analytical and numerical tools. Y.K.K. performed research and computed the control-theoretic aspects. R.B. coordinated the study. D.M. and R.B. analyzed the results

and wrote the paper. CORRESPONDING AUTHOR Correspondence to David Mateo. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare that they have no competing interests. ADDITIONAL

INFORMATION PUBLISHER'S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. ELECTRONIC SUPPLEMENTARY MATERIAL

SUPPLEMENTARY INFORMATION SUPPLEMENTARY VIDEO SUPPLEMENTARY VIDEO SUPPLEMENTARY VIDEO RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0

International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the

source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative

Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Mateo, D., Kuan, Y.K. & Bouffanais, R. Effect of Correlations in Swarms on

Collective Response. _Sci Rep_ 7, 10388 (2017). https://doi.org/10.1038/s41598-017-09830-w Download citation * Received: 10 May 2017 * Accepted: 31 July 2017 * Published: 04 September 2017 *

DOI: https://doi.org/10.1038/s41598-017-09830-w SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is

not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative