Two-dimensional supersolidity in a dipolar quantum gas

ABSTRACT Supersolid states simultaneously feature properties typically associated with a solid and with a superfluid. Like a solid, they possess crystalline order, manifesting as a periodic

modulation of the particle density; but unlike a typical solid, they also have superfluid properties, resulting from coherent particle delocalization across the system. Such states were

initially envisioned in the context of bulk solid helium, as a possible answer to the question of whether a solid could have superfluid properties1,2,3,4,5. Although supersolidity has not

been observed in solid helium (despite much effort)6, ultracold atomic gases provide an alternative approach, recently enabling the observation and study of supersolids with dipolar

atoms7,8,9,10,11,12,13,14,15,16. However, unlike the proposed phenomena in helium, these gaseous systems have so far only shown supersolidity along a single direction. Here we demonstrate

the extension of supersolid properties into two dimensions by preparing a supersolid quantum gas of dysprosium atoms on both sides of a structural phase transition similar to those occurring

in ionic chains17,18,19,20, quantum wires21,22 and theoretically in chains of individual dipolar particles23,24. This opens the possibility of studying rich excitation

properties25,26,27,28, including vortex formation29,30,31, and ground-state phases with varied geometrical structure7,32 in a highly flexible and controllable system. Access through your

institution Buy or subscribe This is a preview of subscription content, access via your institution ACCESS OPTIONS Access through your institution Access Nature and 54 other Nature Portfolio

journals Get Nature+, our best-value online-access subscription $32.99 / 30 days cancel any time Learn more Subscribe to this journal Receive 51 print issues and online access $199.00 per

year only $3.90 per issue Learn more Buy this article * Purchase on SpringerLink * Instant access to full article PDF Buy now Prices may be subject to local taxes which are calculated during

checkout ADDITIONAL ACCESS OPTIONS: * Log in * Learn about institutional subscriptions * Read our FAQs * Contact customer support SIMILAR CONTENT BEING VIEWED BY OTHERS MEASUREMENT OF THE

SUPERFLUID FRACTION OF A SUPERSOLID BY JOSEPHSON EFFECT Article Open access 08 May 2024 SUPERSOLIDITY IN ULTRACOLD DIPOLAR GASES Article 09 October 2023 PHASE COHERENCE IN OUT-OF-EQUILIBRIUM

SUPERSOLID STATES OF ULTRACOLD DIPOLAR ATOMS Article 04 January 2021 DATA AVAILABILITY Data pertaining to this work can be found at https://doi.org/10.5281/zenodo.4729519. CODE AVAILABILITY

Code used for this work is available from the corresponding author upon reasonable request. REFERENCES * Gross, E. P. Unified theory of interacting bosons. _Phys. Rev_. 106, 161–162 (1957).

Article  ADS  CAS  MATH  Google Scholar  * Gross, E. P. Classical theory of boson wave fields. _Ann. Phys_. 4, 57–74 (1958). Article  ADS  MathSciNet  MATH  Google Scholar  * Andreev, A. F.

& Lifshitz, I. M. Quantum theory of defects in crystals. _Sov. Phys. JETP_ 29, 1107–1114 (1969). ADS  Google Scholar  * Chester, G. V. Speculations on Bose–Einstein condensation and

quantum crystals. _Phys. Rev. A_ 2, 256–258 (1970). Article  ADS  Google Scholar  * Leggett, A. J. Can a solid be “superfluid”? _Phys. Rev. Lett_. 25, 1543–1546 (1970). Article  ADS  CAS 

Google Scholar  * Chan, M. H.-W., Hallock, R. & Reatto, L. Overview on solid 4He and the issue of supersolidity. _J. Low Temp. Phys_. 172, 317–363 (2013). Article  ADS  CAS  Google

Scholar  * Lu, Z.-K., Li, Y., Petrov, D. S. & Shlyapnikov, G. V. Stable dilute supersolid of two-dimensional dipolar bosons. _Phys. Rev. Lett_. 115, 075303 (2015). Article  ADS  PubMed 

CAS  Google Scholar  * Baillie, D. & Blakie, P. B. Droplet crystal ground states of a dipolar Bose gas. _Phys. Rev. Lett_. 121, 195301 (2018). Article  ADS  CAS  PubMed  Google Scholar 

* Roccuzzo, S. M. & Ancilotto, F. Supersolid behavior of a dipolar Bose–Einstein condensate confined in a tube. _Phys. Rev. A_ 99, 041601 (2019). Article  ADS  CAS  Google Scholar  *

Boninsegni, M. & Prokof’ev, N. V. Colloquium: Super-solids: what and where are they? _Rev. Mod. Phys_. 84, 759–776 (2012). Article  ADS  CAS  Google Scholar  * Tanzi, L. et al.

Observation of a dipolar quantum gas with metastable supersolid properties. _Phys. Rev. Lett_. 122, 130405 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Böttcher, F. et al. Transient

supersolid properties in an array of dipolar quantum droplets. _Phys. Rev. X_ 9, 011051 (2019). Google Scholar  * Chomaz, L. et al. Long-lived and transient supersolid behaviors in dipolar

quantum gases. _Phys. Rev. X_ 9, 021012 (2019). CAS  Google Scholar  * Guo, M. et al. The low-energy Goldstone mode in a trapped dipolar super-solid. _Nature_ 574, 386–389 (2019). Article 

ADS  CAS  PubMed  Google Scholar  * Natale, G. et al. Excitation spectrum of a trapped dipolar supersolid and its experimental evidence. _Phys. Rev. Lett_. 123, 050402 (2019). Article  ADS 

CAS  PubMed  Google Scholar  * Tanzi, L. et al. Supersolid symmetry breaking from compressional oscillations in a dipolar quantum gas. _Nature_ 574, 382–385 (2019). Article  ADS  CAS  PubMed

  Google Scholar  * Birkl, G., Kassner, S. & Walther, H. Multiple-shell structures of laser-cooled 24Mg+ ions in a quadrupole storage ring. _Nature_ 357, 310–313 (1992). Article  ADS 

CAS  Google Scholar  * Raizen, M. G., Gilligan, J. M., Bergquist, J. C., Itano, W. M. & Wineland, D. J. Ionic crystals in a linear Paul trap. _Phys. Rev. A_ 45, 6493–6501 (1992). Article

  ADS  CAS  PubMed  Google Scholar  * Fishman, S., De Chiara, G., Calarco, T. & Morigi, G. Structural phase transitions in low-dimensional ion crystals. _Phys. Rev. B_ 77, 064111 (2008).

Article  ADS  CAS  Google Scholar  * Shimshoni, E., Morigi, G. & Fishman, S. Quantum zigzag transition in ion chains. _Phys. Rev. Lett_. 106, 010401 (2011). Article  ADS  PubMed  CAS 

Google Scholar  * Hew, W. K. et al. Incipient formation of an electron lattice in a weakly confined quantum wire. _Phys. Rev. Lett_. 102, 056804 (2009). Article  ADS  CAS  PubMed  Google

Scholar  * Mehta, A. C., Umrigar, C. J., Meyer, J. S. & Baranger, H. U. Zigzag phase transition in quantum wires. _Phys. Rev. Lett_. 110, 246802 (2013). Article  ADS  PubMed  CAS  Google

Scholar  * Astrakharchik, G. E., Morigi, G., De Chiara, G. & Boronat, J. Ground state of low-dimensional dipolar gases: linear and zigzag chains. _Phys. Rev. A_ 78, 063622 (2008).

Article  ADS  CAS  Google Scholar  * Ruhman, J., Dalla Torre, E. G., Huber, S. D. & Altman, E. Nonlocal order in elongated dipolar gases. _Phys. Rev. B_ 85, 125121 (2012). Article  ADS 

CAS  Google Scholar  * Santos, L., Shlyapnikov, G. V. & Lewenstein, M. Roton-maxon spectrum and stability of trapped dipolar Bose–Einstein condensates. _Phys. Rev. Lett_. 90, 250403

(2003). Article  ADS  CAS  PubMed  Google Scholar  * Ronen, S., Bortolotti, D. C. E. & Bohn, J. L. Radial and angular rotons in trapped dipolar gases. _Phys. Rev. Lett_. 98, 030406

(2007). Article  ADS  PubMed  CAS  Google Scholar  * Wilson, R. M., Ronen, S., Bohn, J. L. & Pu, H. Manifestations of the roton mode in dipolar Bose–Einstein condensates. _Phys. Rev.

Lett_. 100, 245302 (2008). Article  ADS  PubMed  CAS  Google Scholar  * Bisset, R. N., Baillie, D. & Blakie, P. B. Roton excitations in a trapped dipolar Bose–Einstein condensate. _Phys.

Rev. A_ 88, 043606 (2013). Article  ADS  CAS  Google Scholar  * Gallemí, A., Roccuzzo, S. M., Stringari, S. & Recati, A. Quantized vortices in dipolar supersolid Bose–Einstein-condensed

gases. _Phys. Rev. A_ 102, 023322 (2020). Article  ADS  Google Scholar  * Roccuzzo, S. M., Gallemí, A., Recati, A. & Stringari, S. Rotating a supersolid dipolar gas. _Phys. Rev. Lett_.

124, 045702 (2020). Article  ADS  CAS  PubMed  Google Scholar  * Ancilotto, F., Barranco, M., Pi, M. & Reatto, L. Vortex properties in the extended supersolid phase of dipolar

Bose–Einstein condensates. _Phys. Rev. A_ 103, 033314 (2021). Article  ADS  CAS  Google Scholar  * Zhang, Y.-C., Maucher, F. & Pohl, T. Supersolidity around a critical point in dipolar

Bose–Einstein condensates. _Phys. Rev. Lett_. 123, 015301 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Li, J.-R. et al. A stripe phase with supersolid properties in

spin–orbit-coupled Bose–Einstein condensates. _Nature_ 543, 91–94 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Léonard, J., Morales, A., Zupancic, P., Esslinger, T. & Donner, T.

Supersolid formation in a quantum gas breaking a continuous translational symmetry. _Nature_ 543, 87–90 (2017). Article  ADS  PubMed  CAS  Google Scholar  * Kadau, H. et al. Observing the

Rosensweig instability of a quantum ferrofluid. _Nature_ 530, 194–197 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Ferrier-Barbut, I., Kadau, H., Schmitt, M., Wenzel, M. & Pfau,

T. Observation of quantum droplets in a strongly dipolar Bose gas. _Phys. Rev. Lett_. 116, 215301 (2016). Article  ADS  PubMed  CAS  Google Scholar  * Chomaz, L. et al.

Quantum-fluctuation-driven crossover from a dilute Bose–Einstein condensate to a macrodroplet in a dipolar quantum fluid. _Phys. Rev. X_ 6, 041039 (2016). Google Scholar  * Wächtler, F.

& Santos, L. Quantum filaments in dipolar Bose–Einstein condensates. _Phys. Rev. A_ 93, 061603 (2016). Article  ADS  CAS  Google Scholar  * Bisset, R. N., Wilson, R. M., Baillie, D.

& Blakie, P. B. Ground-state phase diagram of a dipolar condensate with quantum fluctuations. _Phys. Rev. A_ 94, 033619 (2016). Article  ADS  CAS  Google Scholar  * Lavoine, L. &

Bourdel, T. Beyond-mean-field crossover from one dimension to three dimensions in quantum droplets of binary mixtures. _Phys. Rev. A_ 103, 033312 (2021). Article  ADS  CAS  Google Scholar  *

Sohmen, M. et al. Birth, life, and death of a dipolar supersolid. _Phys. Rev. Lett_. 126, 233401 (2021). Article  ADS  CAS  PubMed  Google Scholar  * Hadzibabic, Z., Stock, S., Battelier,

B., Bretin, V. & Dalibard, J. Interference of an array of independent Bose–Einstein condensates. _Phys. Rev. Lett_. 93, 180403 (2004). Article  ADS  PubMed  CAS  Google Scholar  *

Schmidt, J.-N. et al. Roton excitations in an oblate dipolar quantum gas. _Phys. Rev. Lett_. 126, 193002 (2021). Article  ADS  CAS  PubMed  Google Scholar  * Pyka, K. et al. Topological

defect formation and spontaneous symmetry breaking in ion Coulomb crystals. _Nat. Commun_. 4, 2291 (2013). Article  ADS  CAS  PubMed  Google Scholar  * Ulm, S. et al. Observation of the

Kibble–Zurek scaling law for defect formation in ion crystals. _Nat. Commun_. 4, 2290 (2013). Article  ADS  CAS  PubMed  Google Scholar  * Trautmann, A. et al. Dipolar quantum mixtures of

erbium and dysprosium atoms. _Phys. Rev. Lett_. 121, 213601 (2018). Article  ADS  CAS  PubMed  Google Scholar  * Chomaz, L. et al. Observation of roton mode population in a dipolar quantum

gas. _Nat. Phys_. 14, 442–446 (2018). Article  PubMed  PubMed Central  CAS  Google Scholar  * Lima, A. R. P. & Pelster, A. Quantum fluctuations in dipolar Bose gases. _Phys. Rev. A_ 84,

041604 (2011). Article  ADS  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS We thank the Innsbruck Erbium team, T. Bland, G. Morigi and B. Blakie for discussions. We acknowledge

R. M. W. van Bijnen for developing the code for our eGPE ground-state simulations. The experimental team is financially supported through an ERC Consolidator Grant (RARE, number 681432), an

NFRI grant (MIRARE, number ÖAW0600) of the Austrian Academy of Science, the QuantERA grant MAQS by the Austrian Science Fund FWF number I4391-N. L.S. and F.F. acknowledge the DFG/FWF via FOR

2247/PI2790. M.S. acknowledges support by the Austrian Science Fund FWF within the DK-ALM (number W1259-N27). L.S. thanks the funding by the Deutsche Forschungsgemeinschaft (DFG, German

Research Foundation) under Germany’s Excellence Strategy - EXC-2123 QuantumFrontiers - 390837967. M.A.N. has received funding as an ESQ Postdoctoral Fellow from the European Union’s Horizon

2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement number 801110 and the Austrian Federal Ministry of Education, Science and Research (BMBWF). M.J.M.

acknowledges support through an ESQ Discovery Grant by the Austrian Academy of Sciences. We also acknowledge the Innsbruck Laser Core Facility, financed by the Austrian Federal Ministry of

Science, Research and Economy. Part of the computational results presented have been achieved using the HPC infrastructure LEO of the University of Innsbruck. AUTHOR INFORMATION Author notes

* These authors contributed equally: Matthew A. Norcia, Claudia Politi AUTHORS AND AFFILIATIONS * Institut für Quantenoptik und Quanteninformation, Österreichische Akademie der

Wissenschaften, Innsbruck, Austria Matthew A. Norcia, Claudia Politi, Lauritz Klaus, Maximilian Sohmen, Manfred J. Mark & Francesca Ferlaino * Institut für Experimentalphysik,

Universität Innsbruck, Innsbruck, Austria Claudia Politi, Lauritz Klaus, Elena Poli, Maximilian Sohmen, Manfred J. Mark, Russell N. Bisset & Francesca Ferlaino * Institut für

Theoretische Physik, Leibniz, Universität Hannover, Hanover, Germany Luis Santos Authors * Matthew A. Norcia View author publications You can also search for this author inPubMed Google

Scholar * Claudia Politi View author publications You can also search for this author inPubMed Google Scholar * Lauritz Klaus View author publications You can also search for this author

inPubMed Google Scholar * Elena Poli View author publications You can also search for this author inPubMed Google Scholar * Maximilian Sohmen View author publications You can also search for

this author inPubMed Google Scholar * Manfred J. Mark View author publications You can also search for this author inPubMed Google Scholar * Russell N. Bisset View author publications You

can also search for this author inPubMed Google Scholar * Luis Santos View author publications You can also search for this author inPubMed Google Scholar * Francesca Ferlaino View author

publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS M.A.N., C.P., L.K., M.S., M.J.M. and F.F. contributed experimental work. E.P. and R.N.B. performed eGPE

calculations. L.S. contributed variational model. All authors contributed to interpretation of results and preparation of manuscript. CORRESPONDING AUTHOR Correspondence to Francesca

Ferlaino. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PEER REVIEW INFORMATION _Nature_ thanks the anonymous reviewers for their

contribution to the peer review of this work. PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

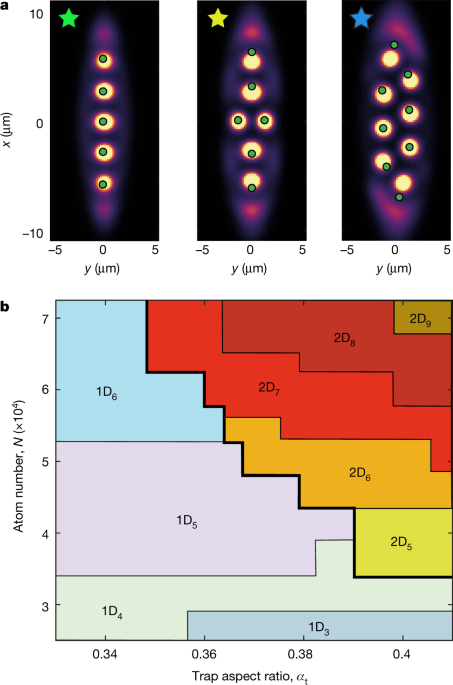
EXTENDED DATA FIGURES AND TABLES EXTENDED DATA FIG. 1 FOURIER TRANSFORMS OF IN-TRAP IMAGES. The upper row shows individual in-trap images for different trap aspect ratios, as shown in Fig.

2b. The lower row shows the data for the same parameters in the Fourier domain, with _k_ the associated wavenumber. As the trap aspect ratio is increased, the modulation goes from being

present along a single direction to two, and a clear hexagonal pattern is visible. EXTENDED DATA FIG. 2 SUPERSOLID DROPLET ARRAY WITH MORE THAN TWO ROWS. A, In-trap image of a droplet array

with more than two rows. B, Averaged Fourier transform of 309 images in conditions of A, showing that a regular modulated structure persists in the more extended system. C, Calculated ground

state from the eGPE for trap parameters (_f__x_, _f__y__, f__z_) = (22, 55, 140) Hz, and _N_ = 60,000 atoms in the droplets, representative of the experimental conditions in A, B. D,

Averaged TOF interference pattern for the conditions of A, B. The inset shows the measured 2D density profile and the main panel shows a radially averaged density, normalized to the peak

density of the averaged image. The grey lines represent individual trials and the red line is the average. The repeatability of the modulation indicates the presence of phase coherence

between droplets. EXTENDED DATA FIG. 3 PROSPECTS FOR LARGER AND ISOTROPIC DROPLET ARRAYS. The panels show eGPE-calculated ground-state density profiles with fixed average atomic density (see

text) and either fixed atom number and trap volume (upper row) or fixed _f__x_ (lower row). Here _N_ refers to the total number of atoms in the simulation (droplets plus halo), in contrast

to the definition used elsewhere to compare with experimental conditions (droplets only). RIGHTS AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Norcia, M.A.,

Politi, C., Klaus, L. _et al._ Two-dimensional supersolidity in a dipolar quantum gas. _Nature_ 596, 357–361 (2021). https://doi.org/10.1038/s41586-021-03725-7 Download citation * Received:

10 February 2021 * Accepted: 14 June 2021 * Published: 18 August 2021 * Issue Date: 19 August 2021 * DOI: https://doi.org/10.1038/s41586-021-03725-7 SHARE THIS ARTICLE Anyone you share the

following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer

Nature SharedIt content-sharing initiative