Using strain to uncover the interplay between two- and three-dimensional charge density waves in high-temperature superconducting yba2cu3oy

ABSTRACT Uniaxial pressure provides an efficient approach to control charge density waves in YBa2Cu3Oy. It can enhance the correlation volume of ubiquitous short-range two-dimensional

charge-density-wave correlations, and induces a long-range three-dimensional charge density wave, otherwise only accessible at large magnetic fields. Here, we use x-ray diffraction to study

the strain dependence of these charge density waves and uncover direct evidence for a form of competition between them. We show that this interplay is qualitatively described by including

strain effects in a nonlinear sigma model of competing superconducting and charge-density-wave orders. Our analysis suggests that strain stabilizes the 3D charge density wave in the regions

between disorder-pinned domains of 2D charge density waves, and that the two orders compete at the boundaries of these domains. No signatures of discommensurations nor of pair density waves

are observed. From a broader perspective, our results underscore the potential of strain tuning as a powerful tool for probing competing orders in quantum materials. SIMILAR CONTENT BEING

VIEWED BY OTHERS TUNING OF CHARGE ORDER BY UNIAXIAL STRESS IN A CUPRATE SUPERCONDUCTOR Article Open access 10 August 2024 SINGLE-DOMAIN STRIPE ORDER IN A HIGH-TEMPERATURE SUPERCONDUCTOR

Article Open access 21 November 2022 COINCIDENT ONSET OF CHARGE ORDER AND PSEUDOGAP IN A HOMOGENEOUS HIGH-TEMPERATURE SUPERCONDUCTOR Article Open access 15 April 2025 INTRODUCTION A tendency

towards charge ordering in the underdoped high-temperature superconducting cuprates was predicted soon after their discovery1,2,3. However, it took decades of effort with a variety of

experimental methods to demonstrate this phenomenon and its ubiquity across the cuprate superconductors4,5,6,7,8,9,10,11,12. This effort has raised many new questions. One observation that

lacks a clear explanation is the fact that the competition between charge order and superconductivity is striking in some cuprate families9,10,13, but is less pronounced in others11,12,14.

Another is the very substantial variation in correlation length, which varies over two orders of magnitude amongst the cuprates families — from a few unit cells to several tens of nm —

without any obvious relation to the superconducting critical temperature _T_c. To address these issues, it has proved useful to focus on materials with low disorder scattering, and to probe

them with external tuning parameters, such as magnetic field10 or pressure15,16,17, that do not introduce disorder. While hydrostatic pressure has been widely used to investigate

unconventional superconductors and correlated electron systems, recent studies have highlighted several benefits of uniaxial stress18,19,20,21. In the cuprates, uniaxial stress has been used

to probe charge stripes in La-based compounds22,23,24, and to polarize them25,26. Interestingly and in contrast to the introduction of pair-breaking impurities27 or vortices under high

magnetic fields10, uniaxial stress can also be used to homogeneously suppress _T_c28. This allows alternative electronic orders to develop, and the interplay between these orders and the

superconductivity to be studied with precision. Uniaxial compression along the _a_ axis (the shortest axis of the orthorhombic structure) has been shown to suppress _T_c by up to 30%28 in

YBa2Cu3O6.67. In this compound, this results in an enhancement of the amplitude and correlation lengths of an incommensurate, short-range, 2D-correlated charge density wave (hereafter

referred to as the 2D CDW)29,30. Beyond a threshold stress value, a long-range-ordered, 3D-correlated CDW (hereafter referred to as the 3D CDW) emerges29,30. 3D CDW order can also be induced

by a magnetic field, though to date, with lower amplitude and shorter correlation lengths than the one induced by uniaxial stress8,31,32,33,34,35. The 2D CDW is biaxial, with components

that propagate along both the _a_ and _b_ axes, while the 3D CDW is uniaxial, propagating along the _b_ axis only. On the other hand, the in-plane wavelengths of the 2D and 3D CDWs are

identical29,32 and the analysis of the in-plane correlation lengths revealed that the 2D CDW consists of quasi-independent unidirectional orders36. This has further been confirmed by the

observation of substantially different dependencies of amplitude and correlation lengths of its _a_ and _b_ components on uniaxial stress30. Overall, this suggests that the 2D and 3D CDWs

might be intimately related. A key question remains to be clarified: does the 3D CDW emerge from “patches” of 2D CDWs that lock together, or is it a separate order, formed by different

charge carriers, whose periodicity locks to that of the background 2D CDWs? Additionally, there is so far little information on where the 3D CDW exists in strain-temperature space, which is

crucial information for understanding its interaction with the superconductivity. Here, we tackle this issue in underdoped YBa2Cu3Oy with synchrotron hard x-ray diffraction under uniaxial

stress. We show that the 2D CDW amplitude stops growing when the 3D CDW onsets, and map the boundaries of the 3D CDW phase in a strain-temperature phase diagram. We further report that the

strain-induced formation of the 3D CDW and its interplay with the 2D CDW and superconductivity are qualitatively well described by including the effects of strain in an extension of a

nonlinear sigma model37 previously used to investigate the magnetic-field-induced formation of the 3D CDW order in YBCO38,39. In this picture, the long-range 3D CDW emerges from the regions

between disorder-induced 2D CDW domains (_i.e_., the regions where superconductivity forms in the absence of strain). The growth of disordered 2D CDW domains is then halted by their

increased surface tension due to phase-mismatch at the boundary with phase-ordered 3D CDW. Finally, we have also looked for signs of discommensurations, which would indicate a tendency of

the CDW to lock to the lattice40, and for pair–density wave (PDW) correlations41 on top of the 3D CDW, but have found no evidence for either. RESULTS Hard x-ray diffraction was performed as

a function of temperature on uniaxially pressurized. YBa2Cu3Oy (YBCO_y_) single crystals, as described in the Methods section. We first discuss the effect of uniaxial compression along the

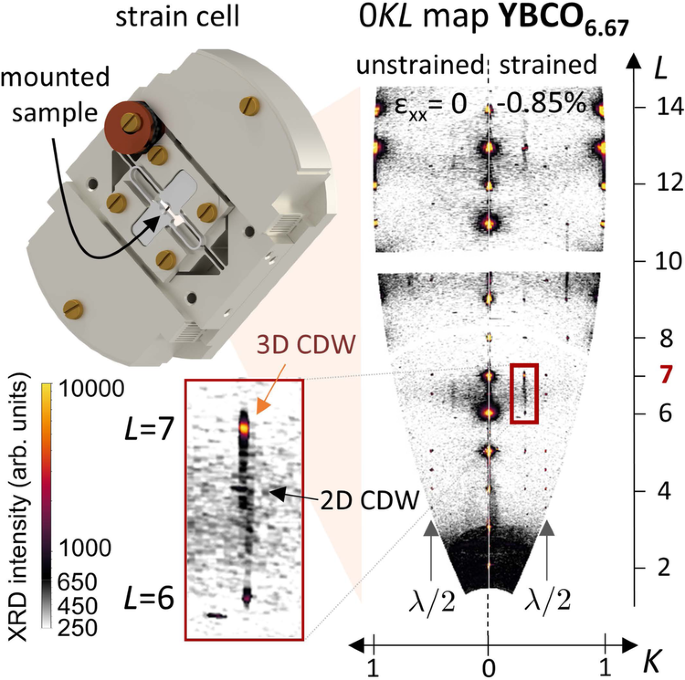
_a_ and _b_ directions on the 2D CDW, for samples with y = 6.67 (corresponding to a doping level _p_ ~ 0.125). As shown in the intensity maps in Fig. 1, the _b_ component of the 2D CDW has

an extremely broad profile along the [0, 0, _L_] direction, centered at half-integer _L_, but is relatively sharp along the [0, _K_, 0] direction already in the absence of strain. The

incommensurate wavevector of the modulations are in perfect agreement with previous reports9,10,27,42. To evaluate the intensity along the _K_ direction, we average the intensity over the

range 0.4 < _L_ < 0.6, with results at a few _a_ axis strain values (_ε__x__x_) shown in Fig. 2a. For these measurements, the temperature is close to _T_c(_ε__x__x_). For strains not

exceeding the 3D CDW onset strain, the 2D CDW is most intense at _T_ ≈ _T_c(_ε__x__x_). It can be seen in Fig. 2a that the intensity of the _b_ component of the 2D CDW approximately doubles

between _ε__x__x_ = 0 and − 0.55% (but the CDW ordering wave vector is only weakly affected by strain). The integrated intensity at a denser set of strains is shown in Fig. 2b, in which this

doubling is again visible, along with a reduction in intensity for _ε__x__x_ < − 0.55%. Also shown in Fig. 2b is the integrated intensity of the _b_ component under compression along the

_b_ axis (_ε__y__y_ < 0). The effect of _b_ axis compression is opposite to that of _a_ axis compression: the intensity shrinks. In Supplementary Fig. 5 we provide evidence confirming

the growth of the _a_ axis component of the 2D CDW under _b_ axis compression, in agreement with previous findings30. Together, these data show that the _a_- and _b_-CDWs are

quasi-independent order parameters, and emphasize the uniaxial nature of the underlying order parameter30,36. The decrease in intensity of the 2D CDW for _ε__x__x_ < − 0.55% coincides

with the onset of the 3D CDW, which manifests itself as a sharp peak at integer _L_, signaling long-range, in-phase correlations along the _c_ axis32,33. The 3D CDW intensity is also shown

in Fig. 2b. It is worth noting that this onset strain is considerably lower than that estimated in previous x-ray scattering studies29,30, in which the lattice parameter along the direction

of compression was not accessible and in which strain could therefore not be determined with sufficient accuracy. It is however closer to the location of an anomaly identified in the stress

dependence of _T_c in ref. 28. The 3D CDW peak is also seen for y = 6.55 (_p_ = 0.108) (see below), but not yet for y = 6.80 (_p_ = 0.140), where, admittedly, the largest strain achieved in

the present work was lower: we reached _ε__x__x_ = − 0.45% (see Supplementary Fig. 6). We turn next to the temperature dependence of the 2D and 3D CDW intensities. Integrated intensities of

the 2D and 3D CDWs versus temperature at selected, fixed strains are shown in Fig. 3a for YBCO6.67, and Fig. 3b for YBCO6.55. At both of the selected strains for both compositions, the 2D

CDW intensity stops increasing (and within experimental accuracy even seems to decrease) when the 3D CDW onsets. At these selected strains, the onset temperature of the 3D CDW exceeds

_T_c(_ε__x__x_ = 0) and so, presuming that _a_ axis compression suppresses _T_c in YBCO6.55 as it does in YBCO6.67 (and as inferred from thermal expansion in the zero stress limit43), it

substantially exceeds _T_c at these strains. Therefore, the end of the 2D CDW growth at these strains is clearly tied to the onset of the 3D CDW, and not to the onset of superconductivity as

at _ε__x__x_ ~ 0. We summarize our findings in the form of intensity maps of the 3D CDW in strain-temperature space, shown for YBCO6.67 and YBCO6.55 in Fig. 3c, d, respectively. For

YBCO6.55 there is no direct measurement of _T_c(_ε__x__x_), so within the 3D CDW phase we estimate this quantity from the temperature where the 3D CDW signal intensity reaches a maximum,

before getting gradually suppressed. This indicates a substantial range of overlap between the 3D CDW and superconductivity. It is, on the one hand, consistent with measurements in high

magnetic fields that systematically find the 3D CDW onset field to lie below _H__c_233, and on the other hand with the 3D CDW signal being observed down to at least 41 K, i.e., well below

_T_c(_ε__x__x_) for YBCO6.67 at the highest measured strain of ref. 29 (the present data allow us to re-estimate this value to be _ε__x__x_ = − 0.85%). For YBCO6.55, the 3D CDW onset lies at

a slightly smaller strain, _ε__x__x_ = − 0.4%, lower than that for YBCO6.67. We end this section with a description of structural changes induced by the 3D CDW formation which can be

quantified, despite experimental limitations on the accessible part of the reciprocal space imposed by the strain cell. Within experimental uncertainty, we observe the main structural

changes in the CuO2-planes as the samples are strained. From structural refinements of YBCO6.67 we observe that the clearest response of the average structure (single unit cell) to the 3D

CDW onset with increasing strain is a growing anisotropy of the buckling angle of the planar oxygen bonds as shown in Supplementary Fig. 7. Minor changes can be discerned in the parameters

of the planar Cu atoms, e.g., in the intra-bilayer distance, but these are less evident than the change observed for the buckling angles of the oxygen bonds. Nevertheless, smaller motions

are to be expected for the heavier Cu atoms. This also finds confirmation in the smaller isotropic temperature factors, shown in Supplementary Fig. 8. MODEL In an effort to elucidate the

experimental findings we consider a nonlinear sigma model describing competition between superconductivity and CDW orders37,38,39. It is formulated in terms of a three-dimensional complex

vector whose components correspond to a superconducting order parameter, _ψ__j__μ_(R), and two complex CDW order parameters, \({\Phi }_{j\mu }^{a,b}({{{{{{{\bf{r}}}}}}}})\). The latter

describe density variations \(\delta {\rho }_{j\mu }({{{{{{{\bf{r}}}}}}}})={e}^{i{{{{{{{{\bf{Q}}}}}}}}}_{a}\cdot {{{{{{{\bf{r}}}}}}}}}{\Phi }_{j\mu

}^{a}({{{{{{{\bf{r}}}}}}}})+{e}^{i{{{{{{{{\bf{Q}}}}}}}}}_{b}\cdot {{{{{{{\bf{r}}}}}}}}}{\Phi }_{j\mu }^{b}({{{{{{{\bf{r}}}}}}}})+{{{{{{{\rm{c.c.}}}}}}}}\), along the _a_ and _b_ directions

with incommensurate wave-vectors Q_a_,_b_. The order parameters reside on bilayers that are indexed by _j_ and represent the CuO2 bilayers of YBCO. The index _μ_ = 0, 1 denotes the bottom

(top) layer and R is the in-plane position vector. In the following we will coarse grain each of the planes into a square lattice whose lattice constant is the observed CDW wavelength,

_i.e_., about 3 Cu-Cu spacings. The model assumes the existence of some type of local order at every lattice point and incorporates the competition between the different components via the

constraints $$| {\psi }_{j\mu }{| }^{2}+| {{{{{{{{\boldsymbol{\Phi }}}}}}}}}_{j\mu }{| }^{2}=1,$$ (1) where \({{{{{{{{\boldsymbol{\Phi }}}}}}}}}_{j\mu }={({\Phi }_{j\mu }^{a},{\Phi }_{j\mu

}^{b})}^{T}\). The vector of order parameters is governed by the Hamiltonian $$H= \mathop{\sum}\limits_{j}\mathop{\sum}\limits_{\mu=0,1}{H}_{j\mu }+\frac{{\rho

}_{s}}{2}\mathop{\sum}\limits_{j}\mathop{\sum}\limits_{{{{{{{{\bf{r}}}}}}}}}\left[\tilde{U}{{{{{{{{\boldsymbol{\Phi }}}}}}}}}_{j,0}^{{{{\dagger}}} }{{{{{{{{\boldsymbol{\Phi

}}}}}}}}}_{j,1}\right.\\ +U{{{{{{{{\boldsymbol{\Phi }}}}}}}}}_{j,1}^{{{{\dagger}}} }{{{{{{{{\boldsymbol{\Phi }}}}}}}}}_{j+1,0}-\tilde{J}{\psi }_{j,0}^{*}{\psi }_{j,1}-J{\psi }_{j,1}^{*}{\psi

}_{j+1,0}\\ +\left.{{{{{{{{\boldsymbol{V}}}}}}}}}_{j}^{{{{\dagger}}} }\left(\gamma {{{{{{{{\boldsymbol{\Phi }}}}}}}}}_{j,0}+{{{{{{{{\boldsymbol{\Phi }}}}}}}}}_{j,1}+{{{{{{{{\boldsymbol{\Phi

}}}}}}}}}_{j+1,0}+\gamma {{{{{{{{\boldsymbol{\Phi }}}}}}}}}_{j+1,1}\right)+{{{{{{{\rm{c.c.}}}}}}}}\right].$$ (2) Henceforth, the bare superconducting stiffness, _ρ__s_, is set to 1 and

serves as the basic energy scale. We model the Coulomb interaction between CDW fields within a bilayer by a local coupling \(\tilde{U}\), and denote the intra-bilayer Josephson tunneling

amplitude by \(\tilde{J}\). The (weaker) Coulomb interaction and Josephson coupling between nearest-neighbor planes belonging to consecutive bilayers are denoted by _U_ and _J_,

respectively. In the last term, we include the coupling between the disordered doped oxygens on the chain layers and the CDW fields on the adjacent bilayers. This coupling may originate from

local changes in the concentration of doped holes and from the Coulomb interaction between the oxygens and the CDW14. Hence, we assume that it is reduced by a factor _γ_ as one moves from

the inner to the outer CuO2 planes. We model the effective potential induced by the chain layers as a collection of randomly placed discs at R_l_, each of radius _r__d_ and containing a

constant potential with a random phase that couples either to the _a_ or _b_ CDW fields, \({{{{{{{\boldsymbol{V}}}}}}}}({{{{{{{\bf{r}}}}}}}})=V{\sum }_{l}f(|

{{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}_{l}| ){e}^{i{\theta }_{l}}{({p}_{l},1-{p}_{l})}^{T}\). Here, _p_ takes the values 0,1 with probability 1/2 and _f_(R) = 1 − Θ(∣R∣ − _r__d_), where

Θ(_r_) is the step function. Within a layer the Hamiltonian reads $$\begin{array}{rcl}{H}_{j\mu }&=&\frac{{\rho }_{s}}{2}\mathop{\sum}\limits_{{{{{{{{\bf{r}}}}}}}}}\left[{\left\vert

{{{{{{{\boldsymbol{\nabla }}}}}}}}{\psi }_{j\mu }\right\vert }^{2}+\lambda | {{{{{{{\boldsymbol{\nabla }}}}}}}}{{{{{{{{\boldsymbol{\Phi }}}}}}}}}_{j\mu }{| }^{2}+g| {{{{{{{{\boldsymbol{\Phi

}}}}}}}}}_{j\mu }{| }^{2}\right.\\ &&+\left.\left(\Delta g-\Delta {g}_{s}\right)| {\Phi }_{j\mu }^{a}{| }^{2}+\Delta {g}_{s}| {\Phi }_{j\mu }^{b}{| }^{2}\right],\end{array}$$ (3)

where _∇_ is the discrete gradient, _λ__ρ__s_ is the CDW stiffness and _g__ρ__s_ is the effective CDW mass reflecting the energetic penalty for CDW ordering. The presence of such a penalty

ensures that superconductivity prevails over the CDW order at _T_ = 0, at least in the disorder-free regions. The mass anisotropy, encapsulated by the Δ_g_ > 0 term, is included as a

result of our assumption that the potential induced by the chain layers favors ordering along the _b_ axis. Finally, and most pertinently to the present study, we assume that the application

of strain causes an increase in the mass of the CDW component along the direction of the strain, while reducing the mass of the transverse component. Specifically, applying compressive

strain in the _a_ direction corresponds to Δ_g__s_ < 0. THEORETICAL RESULTS Our primary interest lies in the _k_-space (measured from Q_a_,_b_) CDW structure factor $${S}_{\alpha

}({{{{{{{\bf{q}}}}}}}},L)= \frac{1}{N}\mathop{\sum}\limits_{{{{{{{{\bf{r}}}}}}}}{{{{{{{{\bf{r}}}}}}}}}^{{\prime} }}\mathop{\sum}\limits_{j{j}^{{\prime} }}\mathop{\sum}\limits_{\mu {\mu

}^{{\prime} }}{e}^{-i\left[{{{{{{{\bf{q}}}}}}}}\cdot \left({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}^{{\prime} }\right)+2\pi \left(j-{j}^{{\prime} }+\frac{\mu -{\mu }^{{\prime}

}}{3}\right)L\right]}\\ \times \langle {\Phi }_{j\mu }^{\alpha }({{{{{{{\bf{r}}}}}}}}){\Phi }_{{j}^{{\prime} }{\mu }^{{\prime} }}^{*\alpha }({{{{{{{{\bf{r}}}}}}}}}^{{\prime} })\rangle,$$ (4)

where _N_ is the number of lattice points, and the averaging is over both thermal fluctuations and disorder realizations. We have used the fact that in YBCO the CuO2 planes within a bilayer

are separated by approximately 1/3 of the _c_ axis lattice constant. We have calculated _S__α_(Q, _L_) by Monte Carlo simulations of Eqs. (2),(3)) on a 32 × 32 × 32 (16 bilayers) system,

with _λ_ = 1, _g_ = 1.1, Δ_g_ = 0.1, \(\tilde{J}=0.15\), _J_ = 0.015, \(\tilde{U}=0.85\), _U_ = 0.12, _V_ = 1, and _γ_ = 0.15. Each data point was averaged over 1000 disorder realizations

with 8 disordered regions per bilayer and _r__d_ = 3 (The disorder potential in an overlap region between two discs with different disorder orientations was taken to be the sum of the

potentials. In the case of two discs with the same orientation the potential in the overlap region was randomly chosen to be one of the two.). Our simulations indicate that the qualitative

trends exhibited by the model are largely insensitive to moderate changes in the model parameters. Below we indicate an instance where one can actually improve the agreement with the

experimental findings by lowering the disorder strength. Our core result is presented in Fig. 4a, which depicts the structure factor at a temperature near the superconducting _T__c_ and for

various values of Δ_g__s_, emulating the effect of _a_ axis strain. For Δ_g__s_ = 0 (absence of strain), both _S__a_ and _S__b_ show broad peaks centered around _L_ = 0.7. This is a result

of CDW domains that nucleate due to interaction with the disorder39. Since a disordered region tends to induce the same CDW pattern on both its flanking planes, an out-of-phase arrangement

of the CDW order tends to form in the _c_-direction. The observed skewness away from _L_ = 1/2 is a result of the form factor in Eq. (4). Increasing Δ_g__s_ towards negative values increases

the energetic cost for nucleating _a_-CDWs and leads to a decrease in the height of the corresponding peak (see inset). An opposite trend is seen for the disorder-induced peak along the _b_

direction. However, a much more dramatic effect emerges in _S__b_ beyond a characteristic value of Δ_g__s_ in the form of a large sharp peak centered at _L_ = 1. This signal originates from

the regions _between_ the disorder-induced CDW domains. It reflects the tipping of the balance between superconductivity and the _b_-CDW order in favor of the latter when the _b_-CDW

nucleation cost is sufficiently reduced. The Coulomb interaction between the strain-induced CDW regions on neighboring bilayers favors an in-phase CDW configuration along the _c_-direction,

hence the peak at _L_ = 1. The sharpness of the peak, which corresponds to a correlation length that is of the order of the system size, is a direct result of the fact that these regions are

not induced by disorder. The same is true for the in-plane correlation length, as shown in Supplementary Fig. 10. The interplay between the superconducting and CDW orders is summarized in

Fig. 4b, which shows the superconducting _T__c_ and the height of the _L_ = 1 CDW peak as a function of the temperature and Δ_g__s_. Clearly, _T__c_ (calculated by finite size analysis of

the superconducting correlation length and renormalized stiffness) is a decreasing function of ∣Δ_g__s_∣ owing to the enhancement of the competing CDW fluctuations. A large 3D CDW signal

appears for Δ_g__s_ ≲ − 0.17 at a temperature that increases with ∣Δ_g__s_∣, peaks in the vicinity of _T__c_ of the strained system and then rapidly diminishes at lower temperatures, as is

also evident in Fig. 4c. This behavior stands in contrast to that of _S__b_(0, _L_ = 1/2), which similarly increases when the temperature is lowered towards _T__c_ but then saturates.

Nevertheless, Supplementary Fig. 9 demonstrates that a moderate decrease in the disorder strength to _V_ = 0.8 causes also _S__b_(0, _L_ = 1/2) to exhibit a peak as a function of

temperature, thus recovering the qualitative experimental trend shown in Fig. 3. Supplementary Fig. 9 shows that at the same time the decreased disorder strength does not significantly alter

the other aspects of the 2D and 3D CDW signals, and in particular their dependence on strain, which we turn to discuss next. Figure 4d depicts the Δ_g__s_ dependence of the 2D and 3D CDW

signals near _T__c_. There is a clear and sharp onset of the 3D CDW peak at Δ_g__s_ ≃ − 0.17, whereas _S__b_(0, _L_ = 1) essentially vanishes at lower values of _a_ axis strain and for all

values of _b_ axis strain (positive Δ_g__s_). The 2D signal, _S__b_(0, _L_ = 1/2), on the other hand, diminishes continuously with decreasing _a_ axis strain and increasing _b_ axis strain.

This is because the accompanying increase in the effective mass of the _b_-CDW successively reduces the magnitude of the CDW induced by the disorder. Interestingly, and similarly to the

experimental observations, we find a saturation and then a slight downturn of the 2D CDW signal that coincides with the onset of the 3D CDW order. We also note that the model predicts that

the in-plane correlation length of the 2D CDW is a very weakly increasing function of the strain, while that of the 3D CDW grows rapidly beyond the onset strain, see Supplementary Fig. 10.

Such behaviour is in accord with previous experimental findings29. DISCUSSION We start our discussion from the structure of the 3D CDW. Having access to large reciprocal space maps and

intense 3D CDW peaks, we can provide strong constraints for deviations from a perfectly sinusoidal charge density modulation in the long-range ordered phase. Previous studies on Bi-based

cuprates44 have indicated that in this system the CDW is commensurate with periodicity _λ_ = 4_a_ over the entire doping range where it appears. More recently, high-field NMR data have been

successfully analyzed in a picture where the CDW is locally commensurate with _λ_ = 3_b_. In both cases it was argued that sharp phase slips (discommensurations) at the CDW domain boundary

could shift the position at which the 3D CDW peak is observed in scattering experiments to an effectively incommensurate value40,44. In this case, one would expect the presence of satellite

peaks at 2_δ_ from Q3D-CDW (_δ_ being the incommensurability to the commensurate 3D CDW wavevector at _k_ = 1/3)40. At _T__c_, for YBCO6.67 we observe no indications for additional satellite

peaks along _b_* coming from such sharp discommensuration (we cannot fully rule out the presence of spatially extended phase slips). We also note that the _K_-cut shown in Fig. 5b for

YBCO6.55 at _T_ = 45 K < _T__c_ does not exhibit a peak at QPDW = Q3D-CDW/2. Such a peak is expected if the observed CDW is due to a PDW, i.e., a modulated superconducting condensate, at

wavevector QPDW, and if the PDW coexists with uniform superconductivity41,45. Based on our measurements, the PDW signal must be at least 50 times smaller than the signal of the long-range 3D

CDW. However, further calculations are needed to estimate the associated periodic lattice displacement and the resulting x-ray intensity to exclude the presence of PDWs. Next, we briefly

discuss our structural results in the context of nematicity, largely associated with the growth of spin and charge-density-wave correlations upon cooling46,47,48,49,50,50 in the cuprates. In

the unstrained orthorhombic unit cell the buckling angles along _a_ and _b_ axes differ only slightly. The increasing trend of the _a_ axis buckling angle under _a_ axis compression

(although the error bars are relatively large compared to this subtle effect) is in line with the anisotropic modulation of the copper-oxygen-bonds with significant out-of-plane

displacements of the oxygen transverse to the 2D CDW modulation inferred from zero field x-ray diffraction51, and can be regarded as a structural parameter possibly related to nematicity.

The fact that this anisotropy appears maximal in the 3D CDW phase, is also consistent with a larger response of the relative quadrupolar splitting in 17O-NMR than in 63Cu-NMR when the 3D CDW

is induced using high magnetic fields40. The buckling anisotropy might therefore be seen as a necessary (but not sufficient) condition for 3D ordering in YBCO, but since the 3D CDW breaks

both rotational and translational symmetry globally, it should not be considered as nematic52. In any event, to better understand the constraints imposed by the crystal structures on the

formation of long-range charge order in the cuprates (in particular given the recent reports on the overdoped side53,54), more systematic structural investigations are needed. We now turn to

the nature of the interplay between the CDW orders and superconductivity. On the one hand, a large body of experiments has unambiguously established that the 2D CDW and superconducting

orders compete in YBCO9,10,42, as both the CDW peak amplitude and the CDW domain correlation length decrease in the superconducting state. On the other hand, in x-ray scattering, the

strongest 3D CDW signals are observed where the homogeneous superconducting phase has been suppressed either by application of a large magnetic field32,33,34,35 or by uniaxial pressure29,30.

In both cases, the maximal achievable strength of the applied perturbations was not sufficient to completely suppress the superconducting state at the lowest temperatures. However, while in

the case of strain tuning the low-temperature superconducting phase is homogeneous with no trace of the 3D CDW, the mixed state of the type-II superconductor in a magnetic field contains

halos of 3D CDW around vortex cores. In the experimental data presented above, we have shown that a form of competition can also manifest itself between the 2D and 3D CDW orders, which is

best evidenced in the region of the strain-temperature space where superconductivity has been suppressed by strain. Data in unstressed YBCO6.67 under applied magnetic field32,33,34,35 can

also be interpreted in terms of this 2D-3D CDW competition. Specifically, it was shown in ref. 35 that as YBCO6.67 is cooled under strong applied field there is a temperature range where the

2D CDW intensity starts to decrease while the 3D CDW keeps increasing. In the same study, a direct conversion of the 2D CDW to the 3D CDW was hypothesized, but the data there do not allow

clean disentanglement of the mutual interaction among the 2D CDW, 3D CDW, and superconductivity. Our data clearly indicate that the 2D CDW stops growing and even shrinks at the onset of the

3D CDW, where the superconductivity would have set in, in the absence of strain. In the superconducting state, the evolution of 2D CDWs is complicated by their mutual competition with the 3D

CDW and the simultaneous competition with superconductivity. Finally, we note that the different temperature- and strain-dependence of the 2D and 3D CDWs can naturally be explained in the

framework of the phenomenological model developed above and is rooted in the different mechanisms that are responsible for their respective establishment. The 2D CDW nucleates in domains

that are dominated by their coupling to the disorder potential that arises from the doped oxygens. Consequently, these domains continue to host the CDW even when superconductivity sets in

within the intervening disorder-free regions. In contrast, the 3D CDW forms in the same intervening regions at large enough strain. By assumption, the strain reduces the energetic cost of

the CDW fluctuations, thus allowing them to appear at temperatures that can even exceed the _T__c_ of the unstrained system. In turn, the growth of the 3D CDW correlations contributes, via

their competition with superconductivity, to the suppression of _T__c_. Below _T__c_ the 3D CDW eventually gives way to the superconducting order, which constitutes the ground state of the

clean model. If the coupling between the dopants and the CDW does not change appreciably between YBCO6.55 and YBCO6.67, then this picture may explain why the 2D CDW is stronger in the latter

(see Supplementary Table 2), as it offers more CDW nucleation centers. Nevertheless, the precise interplay between the CDW and the doped oxygens is not fully understood55. Within the same

picture, the coincident saturation (or shrinkage) of the 2D CDW with the establishment of strong 3D CDW can be traced to phase mismatch between the two types of CDWs. The phase of the 2D CDW

within the disordered domains conforms to the local disorder arrangement, whereas the 3D CDW seeks to establish a uniform phase throughout the system. The phase mismatch along the

boundaries of the disordered domains gives rise to an effective surface tension, via the CDW elastic term in Eq. (3), that consequently arrests the growth of the 2D CDW domains. On a broader

perspective, we believe that our results highlight the inherent strengths of strain tuning as a powerful approach to investigate and manipulate the intricate interplay between competing

orders in quantum materials, hence presenting promising prospects for advancing our understanding of these systems. METHODS SAMPLES High-quality single crystals of YBa2Cu3Oy with oxygen

concentrations 6.55 ≤ y ≤ 6.80 were grown with a flux method and then annealed and detwinned. Their superconducting _T__c_ was measured with SQUID magnetometry42. The crystals were then cut

and polished to needles with dimensions of ≈ 200 _μ_m × 100 _μ_m × 2 mm, and were pressurized along their lengths using a Razorbill CS200T piezoelectric-driven uniaxial stress cell mounted

in a helium flow cryostat. Information about the samples is summarized in Supplementary Table 1. To enable fast sample exchange, the mounting into the stress cell was done via a flexible

titanium support, as displayed in Fig. 1; needles were mounted into these supports in advance, a slow, delicate process, then the supports were mounted into the cell during the beamtime. To

achieve higher stresses, the selected samples were further thinned down laterally using a Xenon plasma focused ion beam (PFIB), as described in Supplementary Note 1. We checked that this

procedure did not alter their superconducting properties. The samples were originally cooled under nominal zero-strain conditions – taking into consideration also the thermal response of the

device used for the measurements – and then strained at low temperatures. X-RAY DIFFRACTION Hard x-ray diffraction was performed at the ID15B beamline of the European Synchrotron Radiation

Facility with a fixed photon energy of 30 keV (_λ_ = 0.413 Å), that enabled us to work in transmission geometry. The scattered photons were collected using a state-of-the-art large area

Dectris Eiger2X CdTe 9M hybrid photon-counting detector. Additional experimental details are given in the Supplementary Note 1 and the original data are available under56,57,58. Rigaku’s

CrysalisPro software59 has been used for data reduction and to obtain reciprocal space maps. Structural refinements of the average unit cell (neglecting oxygen ordering in the chain layer)

have been performed using Jana202060. In spite of the large dynamical range of the detector, the very high intensity difference between the CDW features and the main Bragg reflections

presents a measurement challenge. To map both features, photon flux was adjusted by varying the undulator gap61: high photon flux was used to study CDW superstructure peaks, while low photon

flux was used to record the lattice Bragg peaks without saturating the detector. Additional details about the structure refinements are given in the Supplementary Note 3. STRAIN

DETERMINATION Strains reported in this paper are derived from the Bragg peak positions, eliminating error from uncertainty in strain transmission to the sample. The determination of lattice

parameters was based on integration of about 400 Bragg reflections, a number that was limited by the geometrical constraints imposed by the cryostat and the stress cell, but which is

nevertheless sufficient to allow accurate determination of the three lattice constants _a_, _b_, and _c_. Therefore, we also obtain the Poisson’s ratios, _ν__i__j_ ≡ − _ε__i__i_/_ε__j__j_,

shown in Supplementary Fig. 2. Knowledge of the Poisson’s ratios is useful both as a reference for other measurements, where the scattering geometry might not allow determination of the

longitudinal strain29, and potentially as a thermodynamic probe of possible changes in the electronic structure62. Note that throughout this paper we use the engineering definition of

strain, in which negative values denote compression. DATA AVAILABILITY The data reported in this study are available at56,57,58. The data that support the findings of this study are

available from the corresponding author, upon request. Source data are provided with this paper. CODE AVAILABILITY The code used to generate the Monte Carlo results is included in the 

Supplementary Information. REFERENCES * Zaanen, J. & Gunnarsson, O. Charged magnetic domain lines and the magnetism of high-_T__c_ oxides. _Phys. Rev. B_ 40, 7391–7394 (1989). Article 

ADS  CAS  Google Scholar  * Poilblanc, D. & Rice, T. M. Charged solitons in the Hartree-Fock approximation to the large-_U_ Hubbard model. _Phys. Rev. B_ 39, 9749–9752(R) (1989). Article

  Google Scholar  * Emery, V. J., Kivelson, S. A. & Lin, H. Q. Phase separation in the _t_-_J_ model. _Phys. Rev. Lett._ 64, 475–478 (1990). Article  ADS  CAS  PubMed  Google Scholar  *

Tranquada, J. M., Sternlieb, B. J., Axe, J. D., Nakamura, Y. & Uchida, S. Evidence for stripe correlations of spins and holes in copper-oxide superconductors. _Nature_ 375, 561–563

(1995). Article  ADS  Google Scholar  * Howald, C., Eisaki, H., Kaneko, N., Greven, M. & Kapitulnik, A. Periodic density-of-states modulations in superconducting Bi2Sr2CaCu2O8+_δ_.

_Phys. Rev. B_ 67, 014533 (2003). Article  ADS  Google Scholar  * Hoffman, J. et al. A four unit cell periodic pattern of quasi-particle states surrounding vortex cores in Bi2Sr2CaCu2O8+_δ_.

_Science_ 295, 466–469 (2002). Article  ADS  CAS  PubMed  Google Scholar  * Wise, W. D. et al. Charge-density-wave origin of cuprate checkerboard visualized by scanning tunnelling

microscopy. _Nat. Phys._ 4, 696–699 (2008). Article  CAS  Google Scholar  * Wu, T. et al. Magnetic-field-induced charge-stripe order in the high-temperature superconductor YBa2Cu3O_y_.

_Nature_ 477, 191–194 (2011). Article  ADS  CAS  PubMed  Google Scholar  * Ghiringhelli, G. et al. Long-range incommensurate charge fluctuations in (Y, Nd)Ba2Cu3O6+_x_. _Science_ 337,

821–825 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Chang, J. et al. Direct observation of competition between superconductivity and charge density wave order in YBa2Cu3O6.67. _Nat.

Phys._ 8, 871–876 (2012). Article  CAS  Google Scholar  * Tabis, W. et al. Charge order and its connection with Fermi-liquid charge transport in a pristine high-_T__c_ cuprate. _Nat.

Commun._ 5, 5875 (2014). Article  ADS  CAS  PubMed  Google Scholar  * da Silva Neto, E. H. et al. Ubiquitous interplay between charge ordering and high-temperature superconductivity in

cuprates. _Science_ 343, 393–396 (2014). Article  ADS  PubMed  Google Scholar  * Croft, T. P., Lester, C., Senn, M. S., Bombardi, A. & Hayden, S. M. Charge density wave fluctuations in

La2−_x_Sr_x_CuO4 and their competition with superconductivity. _Phys. Rev. B_ 89, 224513 (2014). Article  ADS  Google Scholar  * Tabis, W. et al. Synchrotron x-ray scattering study of

charge-density-wave order in HgBa2CuO4+_δ_. _Phys. Rev. B_ 96, 134510 (2017). Article  ADS  Google Scholar  * Souliou, S. M. et al. Rapid suppression of the charge density wave in

YBa2Cu3O6.6 under hydrostatic pressure. _Phys. Rev. B_ 97, 020503(R) (2018). Article  ADS  Google Scholar  * Vinograd, I. et al. Nuclear magnetic resonance study of charge density waves

under hydrostatic pressure in YBa2Cu3O_y_. _Phys. Rev. B_ 100, 094502 (2019). Article  ADS  CAS  Google Scholar  * Souliou, S., Bosak, A., Garbarino, G. & Le Tacon, M. Inelastic x-ray

scattering studies of phonon dispersions in superconductors at high pressures. _Superconductor Sci. Technol._ 33, 124004 (2020). Article  ADS  Google Scholar  * Hicks, C. W., Barber, M. E.,

Edkins, S. D., Brodsky, D. O. & Mackenzie, A. P. Piezoelectric-based apparatus for strain tuning. _Rev. Sci. Instrum._ 85, 065003 (2014). Article  ADS  PubMed  Google Scholar  * Hicks,

C. W. et al. Strong increase of _T__c_ of Sr2RuO4 under both tensile and compressive strain. _Science_ 344, 283–285 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Steppke, A. et al.

Strong peak in _T__c_ of Sr2RuO4 under uniaxial pressure. _Science_ 355, eaaf9398 (2017). Article  PubMed  Google Scholar  * Nakata, S. et al. Normal-state charge transport in YBa2Cu3O6.67

under uniaxial stress. _npj Quantum Mater._ 7, 118 (2022). Article  ADS  CAS  Google Scholar  * Boyle, T. J. et al. Large response of charge stripes to uniaxial stress in

La1.475Nd0.4Sr0.125CuO4. _Phys. Rev. Res._ 3, L022004 (2021). Article  ADS  CAS  Google Scholar  * Wang, Q. et al. Uniaxial pressure induced stripe order rotation in La1.88Sr0.12CuO4. _Nat.

Commun._ 13, 1795 (2022). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Gupta, N. K. et al. Tuning charge density wave order and structure via uniaxial stress in a

stripe-ordered cuprate superconductor. _Phys. Rev. B_ 108, L121113 (2023). Article  ADS  CAS  Google Scholar  * Simutis, G. et al. Single-domain stripe order in a high-temperature

superconductor. _Commun. Phys._ 5, 296 (2022). Article  CAS  Google Scholar  * Jakovac, I. et al. Uniaxial stress study of spin and charge stripes in La1.875Ba0.125CuO4 by 139La NMR and 63Cu

NQR. _Phys. Rev. B_ 108, 205113 (2023). Article  ADS  CAS  Google Scholar  * Blanco-Canosa, S. et al. Momentum-dependent charge correlations in YBa2Cu3O6+_δ_ superconductors probed by

resonant x-ray scattering: evidence for three competing phases. _Phys. Rev. Lett._ 110, 187001 (2013). Article  ADS  CAS  PubMed  Google Scholar  * Barber, M. E. et al. Dependence of _T_c of

YBa2Cu3O6.67 on in-plane uniaxial stress. _Phys. Rev. B_ 106, 184516 (2022). Article  ADS  CAS  Google Scholar  * Kim, H.-H. et al. Uniaxial pressure control of competing orders in a

high-temperature superconductor. _Science_ 362, 1040–1044 (2018). Article  ADS  CAS  PubMed  Google Scholar  * Kim, H.-H. et al. Charge density waves in YBa2Cu3O6.67 probed by resonant x-ray

scattering under uniaxial compression. _Phys. Rev. Lett._ 126, 037002 (2021). Article  ADS  CAS  PubMed  Google Scholar  * Wu, T. et al. Emergence of charge order from the vortex state of a

high-temperature superconductor. _Nat. Commun._ 4, 2113 (2013). Article  ADS  PubMed  Google Scholar  * Gerber, S. et al. Three-dimensional charge density wave order in YBa2Cu3O6.67 at high

magnetic fields. _Science_ 350, 949–952 (2015). Article  CAS  PubMed  Google Scholar  * Chang, J. et al. Magnetic field controlled charge density wave coupling in underdoped YBa2Cu3O6+_x_.

_Nat. Commun._ 7, 11494 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Jang, H. et al. Ideal charge-density-wave order in the high-field state of superconducting YBCO.

_Proc. Nat. Acad. Sci. USA_ 113, 14645–14650 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Choi, J. et al. Spatially inhomogeneous competition between

superconductivity and the charge density wave in YBa2Cu3O6.67. _Nat. Commun._ 11, 1–8 (2020). Article  ADS  CAS  Google Scholar  * Comin, R. et al. Broken translational and rotational

symmetry via charge stripe order in underdoped YBa2Cu3O_y_. _Science_ 347, 1335–1339 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Hayward, L. E., Hawthorn, D. G., Melko, R. G. &

Sachdev, S. Angular fluctuations of a multicomponent order describe the pseudogap of YBa2Cu3O6+_x_. _Science_ 343, 1336–1339 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Caplan, Y.,

Wachtel, W. & Orgad, D. Long-range order and pinning of charge-density waves in competition with superconductivity. _Phys. Rev. B_ 92, 224504 (2015). Article  ADS  Google Scholar  *

Caplan, Y. & Orgad, D. Dimensional crossover of charge-density wave correlations in the cuprates. _Phys. Rev. Lett._ 119, 107002 (2017). Article  ADS  PubMed  Google Scholar  * Vinograd,

I. et al. Locally commensurate charge-density wave with three-unit-cell periodicity in YBa2Cu3O_y_. _Nat. Commun._ 12, 3274 (2021). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar

  * Agterberg, D. F. et al. The physics of pair-density waves: cuprate superconductors and beyond. _Annu. Rev. Condens. Matter Phys._ 11, 231–270 (2020). Article  ADS  CAS  Google Scholar  *

Blanco-Canosa, S. et al. Resonant x-ray scattering study of charge-density wave correlations in YBa2Cu3O6+_x_. _Phys. Rev. B_ 90, 054513 (2014). Article  ADS  CAS  Google Scholar  * Kraut,

O. et al. Uniaxial pressure dependence of Tc of untwinned YBa2Cu3O_x_ single crystals for _x_= 6.5-7. _Phys. C: Superconductivity_ 205, 139–146 (1993). Article  ADS  CAS  Google Scholar  *

Mesaros, A. et al. Commensurate 4_a_0-period charge density modulations throughout the Bi2Sr2CaCu2O8+x pseudogap regime. _Proc. Nat. Acad. Sci. USA_ 113, 12661–12666 (2016). Article  ADS 

CAS  PubMed  PubMed Central  Google Scholar  * Blackburn, E. et al. Searching for the signature of a pair density wave in YBa2Cu3O6.67 using high energy x-ray diffraction. Preprint at

http://arxiv.org/abs/2310.18302 (2023). * Ando, Y., Segawa, K., Komiya, S. & Lavrov, A. N. Electrical resistivity anisotropy from self-organized one dimensionality in high-temperature

superconductors. _Phys. Rev. Lett._ 88, 137005 (2002). Article  ADS  PubMed  Google Scholar  * Cyr-Choinière, O. et al. Two types of nematicity in the phase diagram of the cuprate

superconductor YBa2Cu3O_y_. _Phys. Rev. B_ 92, 224502 (2015). Article  ADS  Google Scholar  * Wu, T. et al. Incipient charge order observed by NMR in the normal state of YBa2Cu3O_y_. _Nat.

Commun._ 6, 6438 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Sato, Y. et al. Thermodynamic evidence for a nematic phase transition at the onset of the pseudogap in YBa2Cu3O_y_.

_Nat. Phys._ 13, 1074–1078 (2017). Article  CAS  Google Scholar  * Frachet, M. et al. High magnetic field ultrasound study of spin freezing in La1.88Sr0.12CuO4. _Phys. Rev. B_ 103, 115133

(2021). Article  ADS  CAS  Google Scholar  * Forgan, E. M. et al. The microscopic structure of charge density waves in underdoped YBa2Cu3O6.54 revealed by X-ray diffraction. _Nat. Commun._

6, 10064 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Grissonnanche, G. et al. No nematicity at the onset temperature of the pseudogap phase in the cuprate superconductor

yba2cu3o_y_. _Phys. Rev. X_ 13, 031010 (2023). CAS  Google Scholar  * Peng, Y. Y. et al. Re-entrant charge order in overdoped (Bi, Pb)2.12Sr1.88CuO6+_δ_ outside the pseudogap regime. _Nat.

Mater._ 17, 697–702 (2018). Article  ADS  CAS  PubMed  Google Scholar  * Tam, C. C. et al. Charge density waves and Fermi surface reconstruction in the clean overdoped cuprate superconductor

Tl2Ba2CuO6+_δ_. _Nat. Commun._ 13, 570 (2022). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Achkar, A. J. et al. Impact of quenched oxygen disorder on charge density wave

order in YBa2Cu3O6+_x_. _Phys. Rev. Lett._ 113, 107002 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Frachet, M. et al. Stress-induced structural changes in high-temperature

superconducting YBCO [dataset]. European Synchrotron Radiation Facility (2023). https://doi.org/10.15151/ESRF-DC-1431862596. * Frachet, M. et al. Stress-induced structural changes in

high-temperature superconducting YBCO [dataset]. European Synchrotron Radiation Facility (2023). https://doi.org/10.15151/ESRF-DC-1431859433. * Haghighirad, A.-A. et al. Investigation of the

charge order and the crystal structure in uniaxially pressurized YBa2Cu3O6+_x_ [dataset]. European Synchrotron Radiation Facility (2025). https://doi.org/10.15151/ESRF-ES-787696501. *

Rigaku Oxford Diffraction Ltd, Yarnton, Oxfordshire, E 2015 CrysAlis PRO. * Petříček, V. et al. Crystallographic Computing System JANA2006: General features. _Zeitschrift für

Kristallographie - Crystalline Mater._ 238, 271–282 (2023). Article  CAS  Google Scholar  * Kunz, C. Synchrotron radiation: third generation sources. _J. Phys.: Condens. Matter_ 13, 7499

(2001). ADS  CAS  Google Scholar  * Noad, H. M. L. et al. Giant lattice softening at a Lifshitz transition in Sr2RuO4. _Science_ 382, 447–450 (2023). Article  ADS  CAS  PubMed  Google

Scholar  Download references ACKNOWLEDGEMENTS We thank M. Dušek, M. Hanfland, S. Kivelson, A. P. Mackenzie, V. Petr^íček, J. Schmalian and R. Willa for helpful discussions, A. K. Jaiswal for

SQUID measurements, A. Ghiami and M. Hesselschwerdt for technical support and T. Poreba and N. Maraytta for support during the diffraction experiments at the ESRF and IQMT, respectively.

Self-flux growth was performed by the Scientific Facility ‘Crystal Growth’ at Max Planck Institute for Solid State Research, Stuttgart, Germany. This work was supported through the funding

of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), projects 422213477 (TRR 288 projects B03 and A10) and 449386310. S.M.S. acknowledges funding by the DFG -

Projektnummer 441231589, M. F. acknowledges funding by the Alexander von Humboldt Foundation and the Young Investigator Preparation Grant, H. M. L. N. acknowledges support from the Alexander

von Humboldt Foundation through a Research Fellowship for Postdoctoral Researchers, K. I. acknowledges the Japan Society for the Promotion of Science Overseas Research Fellowships and I. V.

acknowledges the Horizon Europe MSCA fellowship 101065694. C.W.H. acknowledges support from the Engineering and Physical Sciences Research Council (U.K.) (EP/X01245X/1). We thank the

European Synchrotron Radiation Facility (ESRF) for provision of synchrotron radiation facilities under proposals number HC-4226 and HC-4865. FUNDING Open Access funding enabled and organized

by Projekt DEAL. AUTHOR INFORMATION Author notes * K. Ishida Present address: Institute for Materials Research, Tohoku University, Sendai, 980-8577, Japan * These authors contributed

equally: I. Vinograd, S. M. Souliou. AUTHORS AND AFFILIATIONS * Institute for Quantum Materials and Technologies, Karlsruhe Institute of Technology, Kaiserstr. 12, D-76131, Karlsruhe,

Germany I. Vinograd, S. M. Souliou, A.-A. Haghighirad, T. Lacmann, M. Frachet, M. Merz & M. Le Tacon * 4th Physical Institute - Solids and Nanostructures, University of Göttingen,

D-37077, Göttingen, Germany I. Vinograd * Racah Institute of Physics, The Hebrew University, Jerusalem, 91904, Israel Y. Caplan & D. Orgad * Karlsruhe Nano Micro Facility (KNMFi),

Karlsruhe Institute of Technology, Kaiserstr. 12, D-76131, Karlsruhe, Germany M. Merz * ESRF, The European Synchrotron, 71, avenue des Martyrs, CS 40220, F-38043, Grenoble Cedex 9, France G.

Garbarino * Max Planck Institute for Solid State Research, Heisenbergstraße 1, D-70569, Stuttgart, Germany Y. Liu, S. Nakata, M. Minola & B. Keimer * Max Planck Institute for Chemical

Physics of Solids, Nöthnitzer Str. 40, D-01187, Dresden, Germany K. Ishida, H. M. L. Noad & C. W. Hicks * School of Physics and Astronomy, University of Birmingham, Birmingham, B15 2TT,

UK C. W. Hicks Authors * I. Vinograd View author publications You can also search for this author inPubMed Google Scholar * S. M. Souliou View author publications You can also search for

this author inPubMed Google Scholar * A.-A. Haghighirad View author publications You can also search for this author inPubMed Google Scholar * T. Lacmann View author publications You can

also search for this author inPubMed Google Scholar * Y. Caplan View author publications You can also search for this author inPubMed Google Scholar * M. Frachet View author publications You

can also search for this author inPubMed Google Scholar * M. Merz View author publications You can also search for this author inPubMed Google Scholar * G. Garbarino View author

publications You can also search for this author inPubMed Google Scholar * Y. Liu View author publications You can also search for this author inPubMed Google Scholar * S. Nakata View author

publications You can also search for this author inPubMed Google Scholar * K. Ishida View author publications You can also search for this author inPubMed Google Scholar * H. M. L. Noad

View author publications You can also search for this author inPubMed Google Scholar * M. Minola View author publications You can also search for this author inPubMed Google Scholar * B.

Keimer View author publications You can also search for this author inPubMed Google Scholar * D. Orgad View author publications You can also search for this author inPubMed Google Scholar *

C. W. Hicks View author publications You can also search for this author inPubMed Google Scholar * M. Le Tacon View author publications You can also search for this author inPubMed Google

Scholar CONTRIBUTIONS The single crystals used in this study were grown and characterized by Y.L., S.N. under the supervision of Ma. Mi. and B.K.Mi. Me. performed the single crystal XRD and

structural refinement at zero strain. The crystal preparation (polishing, FIBing) for the strain cell was done by S.M.S., I.V., H.M. L.N. and K.I. I.V., S.M.S., A.-A.H., T.L., M.F., G.G.

carried out the XRD experiment under strain at the ESRF. I.V. and A.-A.H. performed the structural refinement and the fine analysis of the data. Y. C. and D. O. developed the theoretical

model and performed the calculations. I.V., S.M.S., D.O., C.W.H. and M.L.T. wrote the paper with input from all coauthors. M.L.T. initiated and supervised the project. CORRESPONDING AUTHOR

Correspondence to M. Le Tacon. ETHICS DECLARATIONS COMPETING INTERESTS C.W.H. has 31% ownership of Razorbill Instruments, a company that markets uniaxial pressure cells such as the one used

for this study. All other authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature Communications_ thanks Richard Scalettar and the other, anonymous, reviewer(s)

for their contribution to the peer review of this work. A peer review file is available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional

claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION PEER REVIEW FILE SOURCE DATA SOURCE DATA RIGHTS AND PERMISSIONS OPEN ACCESS This

article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as

you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party

material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s

Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Vinograd, I., Souliou, S.M., Haghighirad, AA.

_et al._ Using strain to uncover the interplay between two- and three-dimensional charge density waves in high-temperature superconducting YBa2Cu3Oy. _Nat Commun_ 15, 3277 (2024).

https://doi.org/10.1038/s41467-024-47540-w Download citation * Received: 29 November 2023 * Accepted: 05 April 2024 * Published: 16 April 2024 * DOI:

https://doi.org/10.1038/s41467-024-47540-w SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative