Layer-dependent exciton polarizability and the brightening of dark excitons in few-layer black phosphorus

ABSTRACT The evolution of excitons from 2D to 3D is of great importance in photo-physics, yet the layer-dependent exciton polarizability hasn’t been investigated in 2D semiconductors. Here,

we determine the exciton polarizabilities for 3- to 11-layer black phosphorus—a direct bandgap semiconductor regardless of the thickness—through frequency-resolved photocurrent measurements

on dual-gate devices and unveil the carrier screening effect in relatively thicker samples. By taking advantage of the broadband photocurrent spectra, we are also able to reveal the exciton

response for higher-index subbands under the gate electrical field. Surprisingly, dark excitons are brightened with intensity even stronger than the allowed transitions above certain

electrical field. Our study not only sheds light on the exciton evolution with sample thickness, but also paves a way for optoelectronic applications of few-layer BP in modulators, tunable

photodetectors, emitters and lasers. SIMILAR CONTENT BEING VIEWED BY OTHERS ANOMALOUS THICKNESS DEPENDENCE OF PHOTOLUMINESCENCE QUANTUM YIELD IN BLACK PHOSPHOROUS Article 06 March 2023

MONOLAYER INDIUM SELENIDE: AN INDIRECT BANDGAP MATERIAL EXHIBITS EFFICIENT BRIGHTENING OF DARK EXCITONS Article Open access 20 February 2024 ORIGINS OF THE LONG-RANGE EXCITON DIFFUSION IN

PEROVSKITE NANOCRYSTAL FILMS: PHOTON RECYCLING VS EXCITON HOPPING Article Open access 01 January 2021 INTRODUCTION Few-layer black phosphorus (BP) is always a direct bandgap semiconductor,

regardless of the thickness1,2,3,4,5,6,7,8,9,10,11. This renders an ideal platform to interrogate the exciton property evolution from quasi-2D to 3D9,12, such as the exciton binding energy13

and the oscillator strength11. Such practice has been hindered in the popular layered transition metal dichalcogenides, such as MoS2 and WSe2, due to the fact that they possess direct

bandgap only in the monolayer form14,15. As another important parameter, the exciton polarizability16,17 of few-layer BP in the out-of-plane direction is responsible for the field-induced

dipole moment and governs the quantum confined Stark effect (QCSE)18,19, manifested by the exciton energy shift under a vertical electrical field. Its exact value and layer dependence are

crucial for electro-optical effect and various optoelectronic applications. However, experimental determination of the exciton polarizability is still lacking, even though a widely tunable

electrical gap with a vertical electrical field has been demonstrated in few-layer BPs through the transport technique20,21,22,23,24. Optical absorption and scanning tunneling microscopy

(STM) studies of few-layer BP controlled by a single gate have revealed the shift of the exciton resonance or the quasiparticle gap25,26,27,28. Nevertheless, such studies struggle to

differentiate the electrical field effect and doping-induced band-filling effect29, therefore the determination of the exciton polarizability could not be achieved. Here, through the

broadband photocurrent spectroscopy30,31,32 of dual-gate few-layer BP devices, we systematically study the pure field-induced shifts of the optical bandgaps for 3- to 11-layer BP and

determine the exciton polarizability. We reveal that a simple quantum well model18,19,33,34 works well for the thin samples but fails in the relatively thick ones, which requires

consideration of free carrier screening35,36,37,38. Meanwhile, we uncover the behavior of higher-index excitons under the field, which was unattainable in previous transport studies. Most

intriguingly, dark excitons are brightened with the symmetry-breaking field26,39, which promises applications in light modulation5,40 with large modulation depth. RESULTS DEVICE FABRICATION

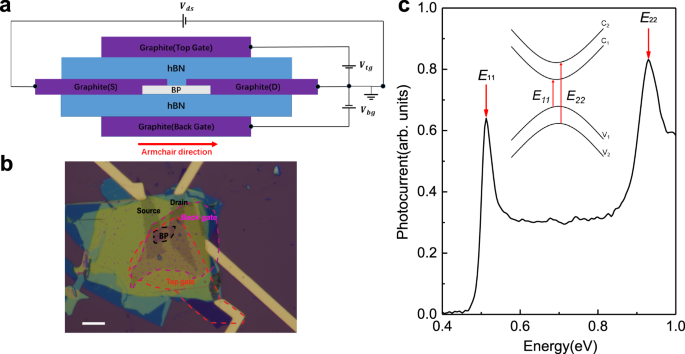
AND CHARACTERIZATION The schematic and optical image of a typical BP photodetector based on a dual-gate transistor structure are shown in Fig. 1a, b, respectively. Here the BP film is in

contact with graphite flakes, which serve as the source and drain electrodes. Sandwiched by hBN flakes, the BP flake was transferred onto a piece of graphite using the polypropylene

carbonate (PPC) hot pick-up technique41. Subsequently, another thin graphite flake was transferred on top. All exfoliation and transfer processes were performed in a nitrogen-filled glovebox

with oxygen and moisture concentrations below 0.1 part per million (ppm) to prevent BP from degradation. Afterwards, chromium-gold electrodes were deposited. Source/drain graphite flakes

were arranged along the armchair direction to maximize the photocurrent5,20,42 (for more details, see Methods). The quality of such hBN/BP/hBN devices can be maintained for a relatively long

period without noticeable degradation43,44,45,46. Photocurrent spectra were obtained by a Fourier transform infrared spectrometer (FTIR) operated in the step-scan mode (See Methods and

Supplementary Fig. 1). Figure 1c shows a typical normalized photocurrent spectrum of an ungated 7-layer BP sample. Detailed normalization process is presented in Supplementary Fig. 3 and

Note 1. Two clear peaks can be identified from Fig. 1c, representing excitons associated with \({E}_{11}\) and \({E}_{22}\) transitions9. Those two peaks, with energies in good agreement

with the absorption spectrum (Supplementary Fig. 2), are originated from transitions from valence subbands to conduction subbands, as shown in the inset of Fig. 1c. Note that the

photocurrent spectrum is equivalent to the absorption spectrum, but it’s more convenient to measure—particularly for such dual-gate devices with multiple stacked 2D materials—due to the less

stringent requirement than that for the absorption measurement in the infrared range, for which, large sample area and simple sample environments are necessary9. QUANTUM CONFINED STARK

EFFECT OF \({{{{{{\BOLDSYMBOL{E}}}}}}}_{{{{{{\MATHBF{11}}}}}}}\) EXCITONS Before detailed photocurrent studies of the Stark effect19, we first performed four-terminal transport measurements

to examine the gating performance of the device. Figure 2a shows the conductance as a function of the back gate voltage (\({V}_{{{{{{\rm{bg}}}}}}}\)) in a 6-layer BP device at different

static top gate bias (\({V}_{{{{{{\rm{tg}}}}}}}\)) ranging from \(-6.0\ {{\mathrm{V}}} \) to \(8.0\ {{\mathrm{V}}} \) at room temperature. In the dual-gate configuration, two electric

displacement fields, \({D}_{{{{{{\rm{t}}}}}}}={\varepsilon }_{0}{\varepsilon }_{{{{{{\rm{b}}}}}}}({V}_{{{{{{\rm{tg}}}}}}}-{V}_{{{{{{\rm{t}}}}}}0})/{d}_{{{{{{\rm{t}}}}}}}\) and

\({D}_{{{{{{\rm{b}}}}}}}={\varepsilon }_{0}{\varepsilon }_{{{{{{\rm{b}}}}}}}({V}_{{{{{{\rm{bg}}}}}}}-{V}_{{{{{{\rm{b}}}}}}0})/{d}_{{{{{{\rm{b}}}}}}}\) are applied in top and back gate

dielectrics to control the doping and electrical field across the thin BP film, where \({\varepsilon }_{{{{{{\rm{b}}}}}}}=3.1\) is the relative permittivity of boron nitride20,

\({d}_{{{{{{\rm{t}}}}}}}\) and \({d}_{{{{{{\rm{b}}}}}}}\) are thicknesses of the top and bottom hBN respectively, and \({V}_{{{{{{\rm{t}}}}}}0}\) and \({V}_{{{{{{\rm{b}}}}}}0}\) are

charge-neutral point voltages due to the unintentional doping respectively. When we decrease \({V}_{{{{{{\rm{tg}}}}}}}\), the position of charge neutral point shifts to higher

\({V}_{{{{{{\rm{bg}}}}}}}\) linearly (Supplementary Fig. 4), with a slope equal to the thickness ratio of the top and back hBN, indicating that the free carriers due to

\({V}_{{{{{{\rm{tg}}}}}}}\) are fully compensated. Recently a few studies determined the change of the electrical gap of BP by transfer curves under certain field20,21,22,24. Our transport

results are fully consistent here. Next, let us examine the frequency-resolved photocurrent and its field dependence. By measuring at charge neutral points determined from its transfer

curve, we eliminate Burstein Moss Shift (BMS)47,48,49,50 caused by Pauli blocking of the optical transitions, rendering an environment with pure vertical electrical field and a fixed Fermi

level within the bandgap, as illustrated in Fig. 2b. The out-of-plane electric field leads to band-bending across the quantum confined system and alters the conduction and valence subband

energies, resulting in the QCSE. Figure 2c shows normalized photocurrent spectra of a 6-layer BP sample at room temperature with different displacement fields. The resonance associated with

the optical bandgap is the major feature of the photocurrent spectrum, consistent with former absorption studies9,11,13. The field we use as our \(x\)-axis is \(D/{\varepsilon }_{0}\) (the

continuity condition gives us \({D}_{{{{{{\rm{b}}}}}}}={D}_{{{{{{\rm{t}}}}}}}={D}_{{{{{{\rm{BP}}}}}}}=D\), with \({D}_{{{{{{\rm{BP}}}}}}}\) as that inside BP). As the electrical field is

applied, the exciton resonant energy hardly changes at low fields and then at higher fields, shifts to lower energy with an increasing rate until the peak becomes too weak under relatively

large fields. The \({E}_{11}\) peak can be continuously tuned from 0.552 eV at zero field to 0.509 eV under a moderate external field of \(1.07\ {{{{{\rm{V}}}}}}\ {{{{{{\rm{nm}}}}}}}^{-1}\),

demonstrating the tunable optical gap in the mid-infrared range. The photocurrent spectra for the reversed field from 0 to \(-0.75\ {{{{{\rm{V}}}}}}\ {{{{{{\rm{nm}}}}}}}^{-1}\) are shown in

Supplementary Fig. 5, exhibiting almost identical response. Figure 2d displays the extracted peak position as a function of the applied field. With the quantum mechanical perturbation

theory and simple symmetry considerations, it has been shown that for symmetric quantum wells, the linear dependence of the energy shift on the electric field vanishes, leaving a quadratic

dependence18,19,33,34, with the coefficient related to the exciton polarizability16,17,25. In other words, due to the symmetry of the quantum well, the unperturbed exciton lacks a dipole

moment along z-direction (out-of-plane). We also carried out the fitting of the 6-layer Stark shift in Fig. 2d with a quadratic dependence: \(E={E}_{0}-\alpha \cdot {(D/{\varepsilon

}_{0})}^{2}\), where the fitting parameter \(\alpha=0.048\ {{{{{\rm{eV}}}}}}\ {{{{{{\rm{nm}}}}}}}^{2}\ {{{{{{\rm{V}}}}}}}^{-2}\) is the exciton polarizability, and \({E}_{0}=0.552\

{{{{{\rm{eV}}}}}}\) is the gap at zero field. The nice quadratic fitting in the figure suggests zero original exciton dipole moment along z-direction, which otherwise contributes a linear

field dependence to the exciton energy shift. Therefore, through the quadratic fitting of the Stark shift, we obtained the exciton polarizability. The same scheme will be applied to other

thickness samples. LAYER-DEPENDENT QCSE OF \({{{{{{\BOLDSYMBOL{E}}}}}}}_{{{{{{\MATHBF{11}}}}}}}\) EXCITONS Now we interrogate the QCSE of \({E}_{11}\) in BP samples of different thickness.

For instance, as we increase the electrical field to \(1.50\ {{{{{\rm{V}}}}}}\ {{{{{{\rm{nm}}}}}}}^{-1}\), \({E}_{11}\) peak of a 3-layer sample shifts from \(0.843\ {{{{{\rm{eV}}}}}}\) to

\(0.827\ {{{{{\rm{eV}}}}}}\), dropping only \(0.016\ {{{{{\rm{eV}}}}}}\) (Supplementary Fig. 6). The shift is apparently smaller than that of the 6-layer sample described in Fig. 2d, which

shifts \(0.022\ {{{{{\rm{eV}}}}}}\) under a much smaller field of \(0.64\ {{{{{\rm{V}}}}}}\ {{{{{{\rm{nm}}}}}}}^{-1}\), indicating the relevance of the sample thickness. We systematically

studied the QCSE for 3- to 11-layer samples and the extracted \({E}_{11}\) peak shifts of representative 3-, 6- and 10-layer BP samples are shown in Fig. 3a, revealing more prominent shifts

for thicker samples. The reproducibility was checked, as shown in Supplementary Fig. 7. As we did for the 6-layer BP in Fig. 2d, we extracted the exciton polarizability α of \({E}_{11}\)

peaks for all 3- to 11-layer BP samples, as shown in Fig. 3b. The extraction process involving fittings is detailed in Supplementary Fig. 8. It’s clear that as the layer number increases,

the polarizability saliently increases. This behavior is qualitatively consistent with the predicted thickness dependence through a simple perturbation method, which gives an \({L}^{4}\)

scaling for the polarizability18,34 (\(L\) is the thickness or layer number). However, our result doesn’t show such dramatic dependence. We tried to fit the experimental polarizability _α_

against layer number \(L\) (proportional to the well width) with a phenomenological polynomial: \(\alpha=A+B\cdot {L}^{C}\). The result is shown in Supplementary Fig. 9 with the power

\(C=0.502\). This suggests the inadequacy of the simple perturbation method. To apprehend the thickness dependence of the QCSE more properly, we performed exact calculations based on an

ideal one-dimensional infinite Quantum Well (QW) under an electric field18,19,33,34. The eigenstates were obtained analytically with the wave functions expressed as linear combinations of

two independent Airy functions (see Supplementary Note 2). By neglecting the field-induced change of the exciton binding energy, shifts of exciton resonant energy under different electric

fields were obtained by summing the shifts of valence and conduction subbands, as shown in Supplementary Fig. 10 (3-layer and 6-layer results are also shown in Fig. 3a as solid curves to

compare with experimental data). We can conclude from the calculation that the shift is enhanced with the growing external field as well as the widening of the QW, which is consistent with

the trend of our experimental data. However, there is quantitative disagreement for relatively thick samples. Supplementary Fig. 11 shows the calculated results and the data of the 10-layer

sample. We can see that the calculation over-estimates the Stark shift. This can be attributed to the arising of the electrostatic screening effect in experiment, possibly due to the

existence of thermal carriers, given that the bandgap is relatively small in few-layer BP and further shrinks with increasing layer number. Such screening makes the local field inside BP

smaller. The signature of the screening is the non-linear shift of charge neutral points in the transfer curve. Previous transport studies have shown that the screening could occur in \(10\

{{{{{\rm{nm}}}}}}\) BP samples21. Although our transport measurements could also affirm the screening effect in BP with similar thickness, as shown in Supplementary Fig. 12 for comparison of

BP samples with 13- and 20-layer (about \(10\ {{{{{\rm{nm}}}}}}\)), it may exist in thinner BP samples, but may not be manifested saliently in the transfer curve. In order to take into

account the screening effect in BP films under different electric fields, we resorted to the nonlinear Thomas-Fermi theory, which has been applied to films of various materials to calculate

the charge distribution and screening35,36,37,38. We also performed calculations of the bandgap dependent carrier density resulted from thermal excitation to verify the feasibility of the

Thomas-Fermi theory. It turns out that for BP samples thicker than 9 layers (about \(4.5\ {{{{{\rm{nm}}}}}}\)), thermally excited free carriers are sufficient and the screening needs to be

considered (see Supplementary Note 4). By still assuming a uniform electric field inside the BP film, we recalculated the QW model under a screened local electrical field. The resulted QCSE

of 10-layer BP is shown by solid line in Fig. 3a. The screened QW model agrees better with experimental results than the QW model for relatively thick samples. This clearly indicates the

necessity for the appropriate electrostatic screening correction. Based on the calculated \({E}_{11}\) energy versus field for 2- to 11-layer devices with both models, now we can extract the

theoretical exciton polarizability \(\alpha\) by fitting the results with a quadratic form, as shown in Fig. 3b. It’s apparent that the QW model gives better description for samples below

8-layer, while the screened QW model works better for thicker ones. Admittedly, neither model can fit the overall data well enough, and more sophisticated theoretical work is required in the

future. INDEX-DEPENDENT QCSE AND THE BRIGHTENING OF DARK EXCITONS Apart from the resonance associated with the optical bandgap, more inclusively, we could gain insights into higher-index

exciton transitions along the way, which were hardly attainable in previous photoluminescence51 and transport20,21,22,24 studies. Typically, devices at cryogenic temperature exhibit better

signal-to-noise ratio in the photocurrent spectroscopy, so that subtle features can be resolved. We measured the photocurrent spectra of a 10-layer sample at \(77.5\ {{{{{\rm{K}}}}}}\).

Figure 4a displays the field dependent photocurrent spectra. Two main peaks can be clearly observed in the ungated spectrum (black line) at \(0.433\ {{{{{\rm{eV}}}}}}\) and \(0.697\

{{{{{\rm{eV}}}}}},\) representing the \({E}_{11}\) and \({E}_{22}\) transitions9. \({E}_{11}\) and \({E}_{22}\) peak positions at different fields were extracted and plotted in Fig. 4b by a

series of blue and orange triangles. As the electrical field increases, \({E}_{11}\) peak shifts to lower energy region, revealing robust QCSE, while \({E}_{22}\) peak shifts much more

slowly. Similar scenario was observed in all 7-layer to 11-layer BP samples, whose \({E}_{22}\) transitions are within the measurement range, such as the 7-layer sample shown in

Supplementary Fig. 13. We carried out calculations for the 10-layer based on the screened QW model33,34,35,36,37,38 and the results are consistent. Supplementary Fig. 14 shows the calculated

evolution of the first (\(l=1\)) and the second (\(l=2\)) valence and conduction subbands. We can see that \(l=1\) subbands shift much quicker than \(l=2\) subbands, indicating

index-dependent QCSE. Typically, the ground state wave function is more sensitive to external perturbations, such as the tilting of the QW potential induced by an vertical field34, than its

excited state counterparts. Hence, \({E}_{11}\) transitions show stronger QCSE. More detailed discussions are presented in Supplementary Note 3. In addition to main peaks, some new features

emerge between them when the field is applied39. Notably, two new peaks arise between \({E}_{11}\) and \({E}_{22}\) (as indicated in Fig. 4a red frame). The scenario fits well with the

brightening of forbidden transitions (dark excitons) and as a result, the peaks could be assigned to forbidden transitions \({E}_{21}\) and \({E}_{12}\) (see the inset of Fig. 4b). As we

know, for a symmetric QW, the dipole selection rule doesn’t allow optical transitions with odd \(\Delta l\) (\(\Delta l\) is the difference between the valence and conduction subband

indices). Only with symmetry breaking, such transitions occur52. With a vertical gate electrical field, the well is not symmetrical anymore, as sketched in Fig. 2b, resulting in the

appearance of dark excitons. Previously, such new peaks, though with weak amplitude, were observed in unintentionally doped few-layer BP in an unpredictable manner9. Importantly, now we can

readily brighten them with a gate field. Owing to the optimized signal to noise ratio, here we can distinguish them clearly and extract the peak positions. Because of the difference in the

effective masses along the out-of-plane direction for the electron and hole, the energies of \({E}_{21}\) and \({E}_{12}\) are slightly different. Previous experiment53 has shown that for BP

films, the splitting of conduction bands is larger than that of valence bands, so \({E}_{21}\) has slightly lower energy, as assigned in Fig. 4a. Supplementary Fig. 15 shows photocurrent

spectra of the same 10-layer BP device at room temperature. Although the signal to noise ratio is not ideal due to the thermal noise, two bumps can still be identified when field increases.

Similar scenario also occurs in other samples, such as the 8-layer BP shown in Supplementary Fig. 16. As expected, \({E}_{21}\) and \({E}_{12}\) transitions also shift with electrical field.

We picked up their peak positions from where the peaks are resolvable (field above \(0.17\ {{{{{\rm{V}}}}}}\ {{{{{{\rm{nm}}}}}}}^{-1}\) experimentally) and display them in Fig. 4b. Both of

the transitions shift to lower energy as the field increases, and the paces are nearly the same. The shifts are largely consistent with our calculations based on the screened QW model, as

shown in Supplementary Fig. 17. As discussed above, \(l=2\) subbands are inert to the field. Consequently, the shift of those two forbidden transitions can be attributed to the \(l=1\)

bands, i.e., \({E}_{21}\) is dominated by the first conduction band \({c}_{1}\) and \({E}_{12}\) by the first valence band \({v}_{1}\). From this point of view, the nearly identical shift

pace of forbidden transitions suggests similar shift rates of bands \({c}_{1}\) and \({v}_{1}\), consistent with calculations as well (Supplementary Fig. 14). The accurate extraction of the

energies of the dark excitons can help us gain deeper insights into the electronic structure of few-layer BP. The energy difference of \({E}_{12}\) and \({E}_{11}\) peaks give us the

splitting of the \(l=1\) and \(l=2\) conduction bands, while the gap between the \(l=1\) and \(l=2\) valence bands can be measured by the difference of \({E}_{21}\) and \({E}_{11}\) peaks.

Such respective splittings cannot be obtained experimentally without resorting to forbidden transitions. By neglecting the shift of bands under relatively small electric field, the original

band splittings of 8- to 10-layer BP system are extracted and shown in Fig. 4c (the spectrum and the peak position extraction of the 8-layer and 9-layer BP are displayed in Supplementary

Fig. 18 and Supplementary Fig. 19). It is apparent that the splitting of conduction bands is larger than that of valence bands, and the \(l=1\) and \(l=2\) bands move closer as the thickness

grows. The shifting trend of band splitting has been calculated in previous studies9,53 with a phenomenological tight binding model, in which the eigenvalues of a N-layer BP system at

Brillouin zone center can be described as: $${E}_{{nj}}={E}_{1j}-2{\gamma }_{j}\,{{\cos }}\,\left(\frac{n\pi }{N+1}\right),$$ (1) where \(\gamma\) stands for the nearest neighbor interlayer

interaction, \(j=c,\, v\) represents the conduction or valence band, \(n={{{{\mathrm{1,2}}}}},\cdots,N\) and \({E}_{1j}\) is the band energy of monolayer BP. The difference of \({E}_{1c}\)

and \({E}_{2c}\) can be calculated by Eq. (1) as: $${E}_{2c}-{E}_{1c}=-2{\gamma }_{c}\left[{{\cos }}\,\left(\frac{2\pi }{N+1}\right)-{{\cos }}\,\left(\frac{\pi }{N+1}\right)\right],$$ (2)

and the same can be applied to valence band as: $${E}_{2v}-{E}_{1v}=-2{\gamma }_{v}\left[{{\cos }}\,\left(\frac{2\pi }{N+1}\right)-{{\cos }}\,\left(\frac{\pi }{N+1}\right)\right].$$ (3) It’s

reasonable to assume that \({\gamma }_{c}\) and \({\gamma }_{v}\) are constants regardless of thickness, the band splitting estimated by Eqs. (2) and (3) both shrink as the layer number

\(N\) becomes larger, perfectly consistent with our data shown in Fig. 3a. Fitting the experimental results by Eqs. (2) and (3) can give us the actual value of the interlayer couplings, that

is \({\gamma }_{c}=0.648\ {{{{{\rm{eV}}}}}}\) and \({\gamma }_{v}=-0.468\ {{{{{\rm{eV}}}}}}\), consistent with previous results calculated from another series of forbidden transitions53. As

the field increases, the forbidden transitions become more and more prominent, as shown in Fig. 4a, indicating that the external field brightens and strengthens these transitions.

Surprisingly, the amplitude of the \({E}_{12}\) transition even becomes stronger than the originally allowed \({E}_{11}\) and \({E}_{22}\) transitions with field exceeding \(0.6\

{{{{{\rm{V}}}}}}\ {{{{{{\rm{nm}}}}}}}^{-1}\). The brightening is fully reversible and readily controllable by the gate field. When an external electrical field is applied, electrons and

holes are dragged towards opposite walls of the well. As a result, the electron and hole envelope wave functions are no longer sinusoidal, and all the overlap integrals are in general

non-zero, brightening the otherwise forbidden transitions. Particularly, the \(\Delta l=1\) forbidden transitions associated with \({c}_{1}\) or \({v}_{1}\) bands appear to be the most

sensitive to the field. To gain insight into the brightening process, we took the intensity ratio between the forbidden transition \({E}_{12}\) and the allowed transition \({E}_{11}\) to

illustrate the enhancement of forbidden transitions under increasing field, given that \({E}_{12}\) is stronger than \({E}_{21}\) and hence provides a more accurate measure. Figure 4d shows

the intensity ratio extracted from spectra in Fig. 4a by Lorentz fittings. It is apparent that the ratio tends to increase with an accelerating speed as the external field grows. Based on

Fermi’s golden rule, we estimated the intensity ratio by computing the overlapping integrals of the envelope wave functions under a vertical field. The numerical calculation result is shown

in Fig. 4e. Detailed calculation method and discussions are presented in Supplementary Note 5. As the electrical field increases, the ratio enlarges significantly. Our experimental result

has the same trend as the calculated counterpart. However, the absolute values differ, and possible reasons are discussed in Supplementary Note 5. Overall, the deviation is reasonable and

qualitatively, our experiment is still quite consistent with our numerical result, unraveling the mechanism for the brightening of dark excitons. The drastic change of the forbidden

transition intensity from zero to even stronger than the allowed ones, suggests that it can provide a new mechanism for light intensity modulation, potentially with large modulation depth.

DISCUSSION The dual-gate configuration in our study is capable of applying a pure electric field on BP, without changing the Fermi level through doping. This is radically different from

previous single gate studies, where Pauli blocking induced Burstein–Moss effects coexists with the QCSE26,29,39. The Burstein–Moss effects caused by the electrostatic doping in BP lead to a

blue shift of the band edge absorption due to the Pauli blocking of lower transition energies. Therefore, the single gate experiments encounter combinations of competing QCSE and

Burstein–Moss effects, leading to nonmonotonic shifts of absorption peaks, as predicted by calculations29. As a comparison, we also tried the single gate configuration. Supplementary Fig. 20

displays the photocurrent spectra of a single-gate 13-layer sample with and without gate voltage. We can see a slight blueshift of the \({E}_{11}\) peak with gate, in sharp contrast to our

dual-gate results, indicating the Burstein–Moss effects overshadow QCSE. This suggests the necessity of dual-gate to truly manifest the QCSE and to extract the exciton polarizability. The

increase of the exciton polarizability is only one of the scenarios when the sample thickness increases. As a matter of fact, another key ingredient in QCSE is the robustness of excitons

under an intense electric field due to the quantum confinement of the electrons and holes. This is most vividly manifested in our 3-layer BP device shown in Supplementary Fig. 6, where the

exciton still has significant oscillator strength with a field as large as \(1.5\ {{{{{\rm{V}}}}}}\ {{{{{{\rm{nm}}}}}}}^{-1}\). When the quantum confinement eases, the oscillator strength of

the exciton becomes more vulnerable to the field, as seen in Supplementary Fig. 23 for the \({E}_{11}\) transition of the 20-layer sample. The intensity of the \({E}_{11}\) exciton already

decreases a lot at \(0.06\ {{{{{\rm{V}}}}}}\ {{{{{{\rm{nm}}}}}}}^{-1}\) and becomes hardly discernable with field above. The scenario is also manifested in 13-layer and 18-layer BP films

shown in Supplementary Figs. 21 and Fig. 22. Based on this trend, it is reasonable to infer that for bulk-like BP, a much smaller field can already separate the electron and hole to a large

extent, resulting in a diminishing exciton oscillator strength. In summary, through meticulous photocurrent spectroscopy of high-quality dual-gate BP devices, we obtained the layer-dependent

\({E}_{11}\) exciton polarizability and revealed the carrier screening effect in relatively thicker samples. This provides insights into the dimensional crossover of excitons in layered

materials. In addition to the lowest energy excitons, we also examined the higher-index subband excitons and brightened dark excitons. Benefiting from the emergence of the forbidden

transitions, we acquired the respective interlayer couplings for the conduction and valence bands. Our work lays the foundation for electro-optics based on BP and underlines the great

potential for optoelectronic applications. METHODS FABRICATION OF HBN-SANDWICHED BP PHOTODETECTORS BP crystals were purchased from HQ Graphene with purity \( > 99.995\%\)54,55. BP thin

flakes were first mechanically exfoliated from bulk crystals onto low viscous polydimethylsiloxane (PDMS) substrates in a nitrogen-filled glovebox with oxygen and moisture concentrations

below 0.1 part per million (ppm). Before transferring, polarization-dependent extinction spectra were measured to characterize the thickness and lattice direction of BP. Shortly afterwards,

the BP flake was assembled together with hBN flakes (thickness measured by a DektakXT profilometer) and graphite electrodes onto silicon substrates covered with a 285-nm thick

\({{{{{\rm{Si}}}}}}{{{{{{\rm{O}}}}}}}_{2}\) using the polypropylene carbonate (PPC) hot pick-up technique described in ref. 41. Then the AZ-5214 photoresist was spun onto the samples and a

Direct Writer (uPG501) was used to define the shape of multiple electrodes. The exposed top hBN layer was etched through the reactive ion beam etching (Trion T2) in a

\({{{{{\rm{S}}}}}}{{{{{{\rm{F}}}}}}}_{6}\) (50 standard cubic centimeter per minute) environment. Finally, chromium/gold (5/85 nm) films were evaporated through thermal evaporation (Nano36)

to form contacts. TRANSPORT AND PHOTOCURRENT MEASUREMENTS The dual-gate transport measurements were performed using a semiconductor characterization system (Keithley 4200). The photocurrent

measurements were then carried out by a FTIR (Bruker Vertex 70 v) in conjunction with a Hyperion 2000 microscope, operated in the step-scan mode. A lock-in amplifier (SR830) was employed to

obtain the photocurrent signal by modulating the light source of a tungsten halogen lamp with a chopper. The lock-in output was fed back to FTIR as the input. The interferogram obtained in

this way was Fourier-transformed by the FTIR software to display spectra in the frequency domain. The low-temperature measurements were carried out in a liquid nitrogen cryostat (Janis

Research ST-300) with a pressure of about \(1\times {10}^{-6}\ {{{{{\rm{mbar}}}}}}\). DATA AVAILABILITY All relevant experimental data are presented in the paper and the Supplementary

Information. The data that support the findings of this study are available from the corresponding author upon request. REFERENCES * Li, L. et al. Black phosphorus field-effect transistors.

_Nat. Nanotechnol._ 9, 372–377 (2014). ADS  CAS  PubMed  Google Scholar  * Rodin, A. S., Carvalho, A. & Castro Neto, A. H. Strain-induced gap modification in black phosphorus. _Phys.

Rev. Lett._ 112, 176801 (2014). ADS  CAS  PubMed  Google Scholar  * Tran, V., Soklaski, R., Liang, Y. & Yang, L. Layer-controlled band gap and anisotropic excitons in few-layer black

phosphorus. _Phys. Rev. B_ 89, 235319 (2014). * Xia, F., Wang, H. & Jia, Y. Rediscovering black phosphorus as an anisotropic layered material for optoelectronics and electronics. _Nat.

Commun._ 5, 4458 (2014). ADS  CAS  PubMed  Google Scholar  * Xia, F. et al. Two-dimensional material nanophotonics. _Nat. Photonics_ 8, 899–907 (2014). ADS  CAS  Google Scholar  * Liu, H. et

al. Phosphorene: an unexplored 2D semiconductor with a high hole mobility. _ACS Nano_ 8, 4033–4041 (2014). CAS  PubMed  Google Scholar  * Castellanos-Gomez, A. et al. Isolation and

characterization of few-layer black phosphorus. _2D Materials_ 1, 025001 (2014). CAS  Google Scholar  * Li, L. et al. Direct observation of the layer-dependent electronic structure in

phosphorene. _Nat. Nanotechnol._ 12, 21–25 (2017). ADS  PubMed  Google Scholar  * Zhang, G. et al. Infrared fingerprints of few-layer black phosphorus. _Nat. Commun._ 8, 14071 (2017). ADS 

CAS  PubMed  PubMed Central  Google Scholar  * Huang, S. et al. Strain-tunable van der Waals interactions in few-layer black phosphorus. _Nat. Commun._ 10, 2447 (2019). ADS  PubMed  PubMed

Central  Google Scholar  * Zhang, G. et al. The optical conductivity of few-layer black phosphorus by infrared spectroscopy. _Nat. Commun._ 11, 1847 (2020). ADS  CAS  PubMed  PubMed Central

  Google Scholar  * Tian, R. et al. Observation of excitonic series in monolayer and few-layer black phosphorus. _Phys. Rev. B_ 101, 235407 (2020). * Zhang, G. et al. Determination of

layer-dependent exciton binding energies in few-layer black phosphorus. _Sci. Adv._ 4, eaap9977 (2018). ADS  PubMed  PubMed Central  Google Scholar  * Mak, K. F. et al. Atomically thin MoS2:

a new direct-gap semiconductor. _Phys. Rev. Lett._ 105, 136805 (2010). ADS  PubMed  Google Scholar  * Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2. _Nano Lett._ 10,

1271–1275 (2010). ADS  CAS  PubMed  Google Scholar  * Empedocles, S. A. & Bawendi, M. G. Quantum-confined stark effect in single CdSe nanocrystallite quantum Dots. _Science_ 278,

2114–2117 (1997). ADS  CAS  PubMed  Google Scholar  * Scott, R. et al. Time-resolved stark spectroscopy in CdSe nanoplatelets: exciton binding energy, polarizability, and field-dependent

radiative rates. _Nano Lett_ 16, 6576–6583 (2016). ADS  CAS  PubMed  Google Scholar  * Bastard, G., Mendez, E. E., Chang, L. L. & Esaki, L. Variational calculations on a quantum well in

an electric field. _Phys. Rev. B_ 28, 3241–3245 (1983). ADS  CAS  Google Scholar  * Miller, D. A. B. et al. Band-edge electroabsorption in quantum well structures: the quantum-confined Stark

effect. _Phys. Rev. Lett._ 53, 2173–2176 (1984). ADS  CAS  Google Scholar  * Chen, X. et al. Widely tunable black phosphorus mid-infrared photodetector. _Nat. Commun._ 8, 1672 (2017). ADS 

PubMed  PubMed Central  Google Scholar  * Deng, B. et al. Efficient electrical control of thin-film black phosphorus bandgap. _Nat. Commun._ 8, 14474 (2017). ADS  CAS  PubMed  PubMed Central

  Google Scholar  * Li, D. et al. Tunable bandgap in few-layer black phosphorus by electrical field. _2D Mater._ 4, 031009 (2017). Google Scholar  * Roldán, R. & Castellanos-Gomez, A. A

new bandgap tuning knob. _Nat. Photonics_ 11, 407–409 (2017). ADS  Google Scholar  * Yan, S.-L. et al. Electrically tunable energy bandgap in dual-gated ultra-thin black phosphorus field

effect transistors. _Chin. Phys. Lett._ 34, 047304 (2017). ADS  Google Scholar  * Liu, Y. et al. Gate-tunable giant Stark effect in few-layer black phosphorus. _Nano Lett._ 17, 1970–1977

(2017). ADS  CAS  PubMed  Google Scholar  * Peng, R. et al. Midinfrared electro-optic modulation in few-layer black phosphorus. _Nano Lett._ 17, 6315–6320 (2017). ADS  CAS  PubMed  Google

Scholar  * Whitney, W. S. et al. Field effect optoelectronic modulation of quantum-confined carriers in black phosphorus. _Nano Lett._ 17, 78–84 (2017). ADS  CAS  PubMed  Google Scholar  *

Yoon, S. et al. Electrical control of anisotropic and tightly bound excitons in bilayer phosphorene. _Phys. Rev. B_ 103, L041407 (2021). * Lin, C., Grassi, R., Low, T. & Helmy, A. S.

Multilayer black phosphorus as a versatile mid-infrared electro-optic material. _Nano Lett._ 16, 1683–1689 (2016). ADS  CAS  PubMed  Google Scholar  * Vanecek, M. & Poruba, A.

Fourier-transform photocurrent spectroscopy of microcrystalline silicon for solar cells. _Appl. Phys. Lett._ 80, 719–721 (2002). ADS  CAS  Google Scholar  * Amani, M. et al. Mid-wave

infrared photoconductors based on black phosphorus-arsenic alloys. _ACS Nano_ 11, 11724–11731 (2017). CAS  PubMed  Google Scholar  * Ju, L. et al. Tunable excitons in bilayer graphene.

_Science_ 358, 907–910 (2017). ADS  CAS  PubMed  Google Scholar  * Miller, D. A. et al. Electric field dependence of optical absorption near the band gap of quantum-well structures. _Phys.

Rev. B Condens. Matter_ 32, 1043–1060 (1985). ADS  CAS  PubMed  Google Scholar  * Matsuura, M. & Kamizato, T. Subbands and excitons in a quantum well in an electric field. _Phys. Rev. B

Condens. Matter_ 33, 8385–8389 (1986). ADS  CAS  PubMed  Google Scholar  * Datta, S. S., Strachan, D. R., Mele, E. J. & Johnson, A. T. C. Surface potentials and layer charge

distributions in few-layer graphene films. _Nano Lett._ 9, 7–11 (2009). ADS  CAS  PubMed  Google Scholar  * Kuroda, M. A., Tersoff, J. & Martyna, G. J. Nonlinear screening in multilayer

graphene systems. _Phys. Rev. Lett._ 106, 116804 (2011). ADS  PubMed  Google Scholar  * Castellanos-Gomez, A. et al. Electric-field screening in atomically thin layers of MoS2: the role of

interlayer coupling. _Adv. Mater._ 25, 899–903 (2013). CAS  PubMed  Google Scholar  * Low, T. et al. Plasmons and screening in monolayer and multilayer black phosphorus. _Phys. Rev. Lett._

113, 106802 (2014). ADS  PubMed  Google Scholar  * Sherrott, M. C. et al. Anisotropic quantum well electro-optics in few-layer black phosphorus. _Nano Lett._ 19, 269–276 (2019). ADS  CAS 

PubMed  Google Scholar  * Sun, Z., Martinez, A. & Wang, F. Optical modulators with 2D layered materials. _Nat. Photonics_ 10, 227–238 (2016). ADS  CAS  Google Scholar  * Pizzocchero, F.

et al. The hot pick-up technique for batch assembly of van der Waals heterostructures. _Nat. Commun._ 7, 11894 (2016). ADS  CAS  PubMed  PubMed Central  Google Scholar  * Guo, Q. et al.

Black phosphorus mid-infrared photodetectors with high gain. _Nano Lett._ 16, 4648–4655 (2016). ADS  CAS  PubMed  Google Scholar  * Liu, Z. et al. Ultrathin high-temperature

oxidation-resistant coatings of hexagonal boron nitride. _Nat. Commun._ 4, 2541 (2013). ADS  PubMed  Google Scholar  * Cao, Y. et al. Quality heterostructures from two-dimensional crystals

unstable in air by their assembly in inert atmosphere. _Nano Lett._ 15, 4914–4921 (2015). ADS  CAS  PubMed  Google Scholar  * Doganov, R. A. et al. Transport properties of pristine few-layer

black phosphorus by van der Waals passivation in an inert atmosphere. _Nat. Commun._ 6, 6647 (2015). ADS  CAS  PubMed  Google Scholar  * Kostoglou, N., Polychronopoulou, K. & Rebholz,

C. Thermal and chemical stability of hexagonal boron nitride (h-BN) nanoplatelets. _Vacuum_ 112, 42–45 (2015). ADS  CAS  Google Scholar  * Burstein, E. Anomalous optical absorption limit in

InSb. _Phys. Rev._ 93, 632–633 (1954). ADS  CAS  Google Scholar  * Moss, T. S. The interpretation of the properties of indium antimonide. _Proc. Phys. Soc. B_ 67, 775 (1954). ADS  Google

Scholar  * Sun, Q. C. et al. Observation of a Burstein–Moss shift in Rhenium-doped MoS2 nanoparticles. _ACS Nano_ 7, 3506–3511 (2013). CAS  PubMed  Google Scholar  * Low, T. et al. Tunable

optical properties of multilayer black phosphorus thin films. _Phys. Rev. B_ 90, 075434 (2014). * Chen, C. et al. Widely tunable mid-infrared light emission in thin-film black phosphorus.

_Sci. Adv._ 6, eaay6134 (2020). ADS  CAS  PubMed  PubMed Central  Google Scholar  * Fox, M. _Optical Properties of Solids Second Edition_ (Oxford University Press Inc., New York, 2010). *

Zhang, G., Huang, S., Chaves, A. & Yan, H. Black phosphorus as tunable Van der Waals quantum wells with high optical quality. _ACS Nano_ 17, 6073–6080 (2023). ADS  CAS  PubMed  Google

Scholar  * Nilges, T., Kersting, M. & Pfeifer, T. A fast low-pressure transport route to large black phosphorus single crystals. _J. Solid State Chem._ 181, 1707–1711 (2008). ADS  CAS 

Google Scholar  * Köpf, M. et al. Access and in situ growth of phosphorene-precursor black phosphorus. _J. Crystal Growth_ 405, 6–10 (2014). ADS  Google Scholar  Download references

ACKNOWLEDGEMENTS H.Y. is grateful to the financial support from the National Key Research and Development Program of China (Grant Nos. 2022YFA1404700,2021YFA1400100), the National Natural

Science Foundation of China (Grant No. 12074085), the Natural Science Foundation of Shanghai (Grant No.23XD1400200). S.H. acknowledges the financial support from the China Postdoctoral

Science Foundation (Grant No. 2020TQ0078). C.W. is grateful to the financial support from the National Natural Science Foundation of China (Grant Nos. 12274030, 11704075) and the National

Key Research and Development Program of China (Grant No. 2022YFA1403400). Part of the experimental work was carried out in the Fudan Nanofabrication Lab. AUTHOR INFORMATION AUTHORS AND

AFFILIATIONS * State Key Laboratory of Surface Physics, Key Laboratory of Micro and Nano-Photonic Structures (Ministry of Education), and Department of Physics, Fudan University, Shanghai,

200433, China Yuchen Lei, Junwei Ma, Jiaming Luo, Shenyang Huang, Boyang Yu, Chaoyu Song, Qiaoxia Xing, Fanjie Wang, Yuangang Xie, Jiasheng Zhang, Lei Mu, Yixuan Ma & Hugen Yan * Centre

for Quantum Physics, Key Laboratory of Advanced Optoelectronic Quantum Architecture and Measurement (MOE), School of Physics, Beijing Institute of Technology, Beijing, 100081, China Chong

Wang * Beijing Key Lab of Nanophotonics & Ultrafine Optoelectronic Systems, School of Physics, Beijing Institute of Technology, Beijing, 100081, China Chong Wang Authors * Yuchen Lei

View author publications You can also search for this author inPubMed Google Scholar * Junwei Ma View author publications You can also search for this author inPubMed Google Scholar *

Jiaming Luo View author publications You can also search for this author inPubMed Google Scholar * Shenyang Huang View author publications You can also search for this author inPubMed Google

Scholar * Boyang Yu View author publications You can also search for this author inPubMed Google Scholar * Chaoyu Song View author publications You can also search for this author inPubMed 

Google Scholar * Qiaoxia Xing View author publications You can also search for this author inPubMed Google Scholar * Fanjie Wang View author publications You can also search for this author

inPubMed Google Scholar * Yuangang Xie View author publications You can also search for this author inPubMed Google Scholar * Jiasheng Zhang View author publications You can also search for

this author inPubMed Google Scholar * Lei Mu View author publications You can also search for this author inPubMed Google Scholar * Yixuan Ma View author publications You can also search for

this author inPubMed Google Scholar * Chong Wang View author publications You can also search for this author inPubMed Google Scholar * Hugen Yan View author publications You can also

search for this author inPubMed Google Scholar CONTRIBUTIONS H.Y. and Y.L. initiated the project and conceived the experiments. Y.L. prepared the samples, performed the measurements and data

analysis with assistance from J.L., S.H., B.Y., F.W., Q.X., C.S., C.W., Y.X., L.M., J.Z., and Y.M. J.M. and Y.L. provided the theoretical support. H.Y. and Y. L. cowrote the paper and all

authors commented on the paper. H.Y. supervised the whole project. CORRESPONDING AUTHOR Correspondence to Hugen Yan. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing

interests. PEER REVIEW PEER REVIEW INFORMATION _Nature Communications_ thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.

ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION

SUPPLEMENTARY INFORMATION PEER REVIEW FILE RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use,

sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative

Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated

otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds

the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and

permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Lei, Y., Ma, J., Luo, J. _et al._ Layer-dependent exciton polarizability and the brightening of dark excitons in few-layer black phosphorus.

_Nat Commun_ 14, 5314 (2023). https://doi.org/10.1038/s41467-023-41126-8 Download citation * Received: 09 December 2022 * Accepted: 24 August 2023 * Published: 01 September 2023 * DOI:

https://doi.org/10.1038/s41467-023-41126-8 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative