Pressure driven rotational isomerism in 2d hybrid perovskites

ABSTRACT Multilayers consisting of alternating soft and hard layers offer enhanced toughness compared to all-hard structures. However, shear instability usually exists in physically

sputtered multilayers because of deformation incompatibility among hard and soft layers. Here, we demonstrate that 2D hybrid organic-inorganic perovskites (HOIP) provide an interesting

platform to study the stress–strain behavior of hard and soft layers undulating with molecular scale periodicity. We investigate the phonon vibrations and photoluminescence properties of

Ruddlesden–Popper perovskites (RPPs) under compression using a diamond anvil cell. The organic spacer due to C4 alkyl chain in RPP buffers compressive stress by tilting (_n_ = 1 RPP) or

step-wise rotational isomerism (_n_ = 2 RPP) during compression, where _n_ is the number of inorganic layers. By examining the pressure threshold of the elastic recovery regime across _n_ = 

1–4 RPPs, we obtained molecular insights into the relationship between structure and deformation resistance in hybrid organic-inorganic perovskites. SIMILAR CONTENT BEING VIEWED BY OTHERS

GIANT PIEZORESISTIVITY IN A VAN DER WAALS MATERIAL INDUCED BY INTRALAYER ATOMIC MOTIONS Article Open access 18 March 2023 ABERRANT ELECTRONIC AND STRUCTURAL ALTERATIONS IN PRESSURE TUNED

PEROVSKITE NAOSO3 Article Open access 16 September 2020 INTERLAYER ENGINEERING OF LATTICE DYNAMICS AND ELASTIC CONSTANTS OF 2D LAYERED NANOMATERIALS UNDER PRESSURE Article Open access 27 May

2025 INTRODUCTION Two-dimensional (2D) Ruddlesden-Popper perovskites (RPPs) consist of alternatively stacked layers of soft organic layers and rigid inorganic layers with highly tunable

optoelectronic properties1,2. The organic layers provide the dielectric and quantum confinement of the inorganic layers, giving rise to large exciton binding energies and high oscillator

strength3,4,5. From a structural mechanics point of view, the inorganic layers serve as mechanical brace to support spring-like molecular layers, forming a “natural” undulating hard-soft

system. In the realm of mechanical engineering, such a hard-soft multilayer system is highly sought after for its high plastic deformation resistance and increased fracture hardness, but

requires a complex fabrication process. The undulating layers create bands of tensile and compressive stress that is different from that of single-component layers, thus research efforts on

inorganic hard-soft multilayers are centered on engineering structure and compositional gradient to enhance the mechanical properties of materials. The general chemical formula for lead

halide 2D RPPs is (RNH3)2Mn−1PbnX3n+1 (_n_ represents the number of inorganic layers), where PbX42- is an inorganic perovskite layer of corner-sharing metal halide octahedra, RNH3+ is a

long-chain alkylammonium organic molecular layer, such as butyl ammonium (BA), and M is a smaller cation filled into the 12-fold coordinated holes wrapped by the PbX6 octahedra, such as

CH3NH3+ (MA+)6,7,8. The long-range structure of the organic array is a result of balancing local strain induced by methyl ammonium ions on the inorganic cage, hydrogen-bonding and

electrostatic forces between the cationic head group of the organic molecule and the metal halide framework9,10. Thanks to the rigid-/soft-layer alternated stacking structure of 2D layered

perovskites, the rigid inorganic framework can template the conformation of the soft organic molecule confined in the organic-inorganic atomic interface11. In the ground state of C4 alkyl

chain, each CH2 moiety adopts the trans-trans (tt) conformation to avoid steric repulsion. Under compression, it can be expected that the lamellar layers will contract and the strain in the

metal halide bonds will affect optical and electronic properties12,13,14,15,16,17,18,19,20,21. However, little is known about the conformational change of the organic cations and the plastic

deformation or strain hardening process when the organic molecules re-orientate under pressure, this is because X-ray diffraction is mostly sensitive to the heavier inorganic components.

Here, using a combination of in situ Raman and Photoluminescence (PL) spectroscopy, we investigate how compressive and tensile strain develops in the organic and inorganic components in

(BA)2MAn−1PbnI3n+1 (_n_ = 1-4) during compression. Combining experiments and density functional theory (DFT), we observed that _n_ = 1 and _n_ > 1 exhibit markedly different mechanisms of

compressive strain under pressure. In _n_ = 2 RPP, under compression, the trans-trans (tt) structure of the butyl ammonium cation gradually transforms into the trans-gauche (tg) and

gauche-gauche (g+g- and g+g+) conformations via C-C and C-N bond rotations, along with tensile strain of the inorganic slabs in both _a_ and _b_ axial directions. In contrast, for _n_ = 1

RPP, tilting of the linear organic cation is along with in-plane shift in one direction (_b_ axis), resulting in orthorhombic-to-monoclinic phase change under compression. _n_ = 1 RPP shows

remarkable elastic recovery ability due to the flexibility of organic cation that acts synergistically with the octahedral tilt of the inorganic cages. Our study shows how differing

alternation of soft and hard layers allows compressive and tensile stress to evolve differently across _n_ = 1 to _n_ = 4 RPPs, which provides the essential experimental basis for

understanding stress-strain behavior in nanometer scale multilayer hard-soft superlattices. RESULTS To lay the groundwork for understanding the complex structural changes in the organic and

inorganic parts of the hybrid perovskites upon hydrostatic compression, it is beneficial to organize the paper by discussing the changes revealed by first-principles calculations first,

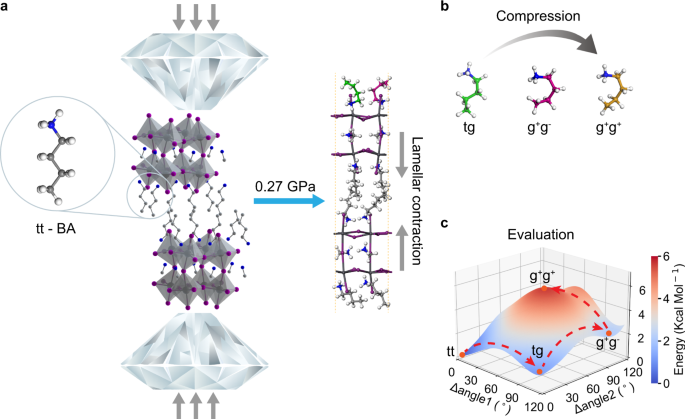
followed by comparison with what was observed in the experiments. THEORETICAL CALCULATIONS OF LAMELLAR CONTRACTION Figure 1a depicts a unit cell of _n_ = 2 RPP. Two layers of interdigitated

linear organic BA molecules alternately stack with two layers of Pb2I73- inorganic slabs. The unit cell height of ~ 2.1 nm is determined by atomic force microscopy (AFM)22. BA organic

molecules in tt conformation dominate the large interlayer spaces, while MA ions occupy the inter-octahedral voids (Supplementary Fig. 1a). In the case of _n_ = 1 RPP, there are no MA ions

and one layer of PbI42- inorganic slab is alternatively stacked with two layers of BA molecules (Supplementary Fig. 2). To simulate hydrostatic compression, a two-step strategy (see

Supplementary Discussion for details) was adopted with the bi-layer RPP sample being sandwiched between two diamond slabs (Fig. 1a and Supplementary Fig. 1a). Under compression, the lamellar

distance contracts. In the low pressure range (<~ 3 GPa), compressive stress is accommodated mainly by the deformation of the organic layers. At 0.27 GPa, the lamellar contraction is

achieved by rotation of the tt isomer of BA to tg (green color) and g+g- (purple color) conformers on the surface of RPP, which can be accomplished by rotating along the C-C/C-N chain (Fig. 

1b). The rotational energy landscape of BA (Fig. 1c) shows that the linear tt isomer is the global minimum state of the BA molecule, which can transform into the tg and g+g- conformers

across a barrier of ~ 1.1-2.8 and ~ 3.2 Kcal/Mol, respectively, as listed in Table S1. Relative to the initial tt state with its energy set to zero as a reference point, the g+g+ conformer

has a higher energy of 4.5 Kcal/Mol (Table S1), therefore it is unstable and  transforms into other conforms readily. The tg isomers are classified into the tg-kind1 and tg-kind2 according

to the asymmetry of tail and head, as shown in the Supplementary Fig. 6, they share similar energy but opposite dihedral angles. The rotation of the organic cations allows the Pb2I73-

inorganic cage to resist deformation at compressive pressure below ~ 3 GPa (Supplementary Fig. 1a). In contrast, the BA molecules are transformed into the BA conformers with the comparable

energies (Table S1), i.e., tg and g+g- isomers are energetic local minimum states, leading to their ambient stability. The ability to generate new rotational conformers in RPP by compression

is subsequently verified in our experiments shown later. Compression results in the layer-to-layer shift of the bi-layer inorganic slabs in _n_ = 2 RPP along _- a_ and _+ b_ axes, as

represented by the blue and grey arrows in Fig. 2a (right side), which is related to a \({M}_{5}^{-}(a,\, b)\) mode23. Such an interlayer shift maintains _n_ = 2 RPP in the orthorhombic

symmetry, accompanied by the conformational change of BA molecules without tilting under pressure. Interestingly, we observed pronounced differences in the pressure response of _n_ = 1 RPP

compared to its higher homologues, as illustrated in Fig. 2. For _n_ = 1 RPP, the linear BA molecules tilt without undergoing conformational change till 7.36 GPa (Supplementary Fig. 2a). The

molecular tilting drives the adjacent inorganic layer to shift in the same direction along _+b_ axis, as represented by the grey arrows in Fig. 2a (left side), which is related to a

\({\Gamma }_{5}^{+}\) mode23. The layer shift decreases the initial stacking offset and therefore the crystal undergoes a phase transition to the monoclinic class24. Such pressure-induced

layer-to-layer shift is however absent in _n_ = 2 RPP ( < ~3 GPa). The detailed structural evolution of _n_ = 1 and _n_ = 2 RPP with pressure is presented in the Supplementary Fig. 4.

IN-PLANE SHIFT The discontinuity in the _c_ direction of 2D RPPs allows an in-plane layer shift between the adjacent inorganic layer, which can be evaluated by a layer shift factor

(_LSF_)25. Here, using the lower inorganic layer as the reference, the relative coordinate deviation of the upper layer along the _a_ axis is calculated as:

$${{LSF}}_{{{{{{\rm{a}}}}}}}={\sum} _{{n}}(\bar{{l}_{1}}-\bar{{l}_{2}})/n{L}_{{{{{{\rm{a}}}}}}}$$ (1) Where \(\bar{{l}_{1}}-\bar{{l}_{2}}\) is one of the in-plane projected vectors of Pb

atoms pair (\({l}_{1}\), \({l}_{2}\)) from the first and second layers in the \(\sqrt{2}\,\times \sqrt{2}\) supercell metric, \({L}_{{{{{{\rm{a}}}}}}}\) is the corresponding lattice

parameter. The standard RPPs have an initial _LSF_ value of 0.25 on both _a_ and _b_ directions25, referring to the Supplementary Fig. 4 for the top views of layer shift between _n_ = 1 and

2 RPPs in the low-pressure region (<~ 3 GPa, where the lamellar contraction is dominated by BA organic layers). The calculated _LSF_ are represented by the green filled circles for _n_ = 

1 in Fig. 2b and green /blue filled cubes for _n_ = 2 in Fig. 2c. The _n_ = 1 RPP has a maximum _LSF__b_ value of ~ 0.34 at 0.24 GPa, while _n_ = 2 RPP accommodates _LSF__a_ of ~ 0.33 and

_LSF__b_ of ~ 0.10 along _- a_ and _b_ directions, respectively. The _n_ = 1 RPP has an average _LSF__b_ value of ~ 0.32 ± 0.01 within pressure of 2.51 GPa, while _n_ = 2 RPP accommodates an

average _LSF__-a_ value of ~ 0.32 ± 0.01 and _LSF__b_ value of ~ 0.14 ± 0.03 along _- a_ and _b_ directions within pressure of 2.31 GPa. Here, the vertical strain is defined as the relative

interlayer distance change comparing that of the initial layer distance, following with this formula: $${\triangle }_{d}=({d}_{{{{{{\rm{p}}}}}}}-{d}_{0})/{d}_{0}$$ (2) where the

\({d}_{{{{{{\rm{p}}}}}}}\) and \({d}_{0}\) are the inorganic interlayer distance at \({{{{{\rm{p}}}}}}\) GPa and \(0\) GPa, respectively. According to our calculations, the tilting of BA

cations in _n_ = 1 RPP results in a vertical strain of ~ 14.6 % within pressure of 2.51 GPa (violet filled circles in Fig. 2b), while the rotation isomerism of BA cations in _n_ = 2 RPP

results in ~ 23.9% vertical strain within pressure of 2.31 GPa (violet filled cubes in Fig. 2c). COMPRESSIBILITY AND OCTAHEDRAL TILT To track the structural deformation and recoverability of

the inorganic sublattice during compression-decompression cycles, we analyze several key structural parameters that represent the in-plane and out-of-plane components of the _n_ = 2 RPP

Pb-I octahedral cage (Fig. 3a), namely, anionic cage angles (β and α), octahedral tilting angles (γ and ɵ) and Pb-I bond lengths (dI1-Pb and dI2-Pb). To track the deviation from the initial

angles at 0 GPa after compression, we monitor the difference in angles ∆θ between the final and initial state. Under compression, _n_ = 2 RPP undergoes lamellar contraction by the rotational

isomerism of the softer BA cations, this allows the harder Pb-I lattice to remain in the elastic regime when the pressure is less than ~ 3 GPa. The apical angle α linking two octahedral

cages serves as a pivot and bends by up to ~ 12.4° during vertical compression, and unbends a little bit more after decompression (red symbols in Fig. 3b). The sudden drop in α beyond ~ 3 

GPa reflects the pressure threshold in the _n_ = 2 system, beyond which irreversible deformation occurs. On the other hand, the change in the equatorial angle β subtends by Pb-I-Pb in the

_ab_ plane (blue symbols in Fig. 3b) reflects the intra-layer compressive strain, ∆β gives a negative difference because the compressed angle is smaller than the angle before compression,

and it shows a distinct drop beyond the same pressure threshold as ∆α. Besides, the structural distortion of the inorganic sublattice can also be revealed by the octahedral tilt, where the

out-of-plane tilt is much more pronounced than the in-plane tilt (solid symbols in Fig. 3d). In the case of _n_ = 1 RPP, lamellar contraction occurs by the tilting of the organic cation

(Supplementary Fig. 2a). The maximum value of the in-plane octahedral tilt (Δγ = 4.5°) and the out-of-plane tilt (Δɵ = 8.4°) (solid symbols in Fig. 3c). These two tilt angles seem to display

good recoverability after decompression as compared to those of _n_ = 2 RPP, as represented by the hollow symbols in Fig. 3c. It suggests that _n_ = 1 RPP resists vertical compression by

the combination of the tilting of organic cation as well as octahedral tilts of the inorganic sublattice. An important difference is that the tilted organic cations in _n_ = 1 RPP can be

untilted upon decompression (Supplementary Fig. 2b), whereas the rotation isomers in _n_ = 2 RPP are locked and cannot be reverted to the original isomers upon decompression (Supplementary

Fig. 1b). The better recovery of bond lengths in _n_ = 1 after decompression can further prove the distinct pressure response of BA molecule between _n_ = 1 and _n_ = 2 RPP, as shown in the

Supplementary Fig. 5. To better understand the organic BA isomerism and inorganic octahedral tilting under finite temperature and pressures, ab initio molecular dynamics simulations (AIMD)

were performed for both _n_ = 1 and 2 RPPs. The free energies for isomerism and lattice tilting were deduced from the probability distribution of inner molecular angles of the BA molecule

and azimuthal angles of the sublattice (Supplementary Figs. 7–9). For the organic part, as shown in the Supplementary Fig. 7c-g, the barrier of the inner molecular rotation of BA within RPP

layers from tt to tg is found to be ~ 0.6-0.9 Kcal/Mol, which is slightly lower than the barrier of ~ 1.1-2.8 Kcal/Mol obtained from DFT calculations (Fig. 1c). More importantly, the stable

tg BA isomer is formed at 0.5 GPa in _n_ = 2 RPP, and a lower energy barrier is obtained upon further compression, e.g., ~ 12.5-25% in decrease at 3.0 GPa (Supplementary Fig. 7e-g). As a

comparison, there is no new stable isomers formed in _n_ = 1 RPP within 10 GPa, and compression will increase the rotation barrier (Supplementary Fig. 7c, d). For the inorganic part, the

Pb-I skeleton shows strong anharmonicity within the dynamic tilting process, as shown in the Supplementary Figs. 8 and 9, and the local skeleton distortion induces a remarkable energy

double-wall potential along the tilting direction. At 5.0 GPa, the more asymmetric potential in _n_ = 2 RPP indicates its stronger octahedral distortion induced by the strong hydrogen bond

interaction between the Pb-I skeleton and BA molecules. The AIMD calculations further verify the distinct pressure response for _n_ = 1 and _n_ = 2 RPP. RAMAN SPECTROSCOPIC EVIDENCE OF

ROTATED BA CONFORMERS Raman spectroscopy is a powerful tool used to characterize the vibrations and rotations of organic molecules in organic-inorganic hybrid perovskites during the

pressurization process26,27. The single crystal of _n_ = 2 RPP was synthesized through a temperature-programmed crystallization method28,29, and the exfoliated flakes were loaded into the

diamond anvil cell (DAC) for in situ high pressure Raman measurement. NaCl was used as the pressure transmitting medium (PTM) to obtain a clean Raman signal of the organic molecular

vibrations. As a reference, we have calculated the Raman spectra of BA+ gas molecule in the tt, tg-kind1 (tg-kind2) and g+g- conformations, as represented by the grey, dark (light) blue and

red solid lines in Fig. 4a, b (See the detailed peak assignment in the Supplementary Discussion). The corresponding calculated vibrational modes are listed in Table S2 and S3. Besides, to

test the effect of Pb-I inorganic lattice on the BA vibrational frequencies, a phononic calculation was also performed for BA isomers in _n_ = 2 RPP structure, as shown in Table S4. The

Raman results show a similar shift behavior during the conformational change similar to that of BA in gas form, thus, the following discussion of Raman results is based on BA+ gas molecules.

Our measured in situ high-pressure Raman spectra of _n_ = 2 RPP under compression, as shown in Fig. 4c, reproduces largely the Raman peak evolutions during the trans to gauge conformational

change of the BA+ gas molecules. The measured Raman bands at 0 GPa in the frequency region of 450 − 890 cm−1 are the skeletal vibrational modes of BA molecules in the tt conformation, as

represented by grey solid line in Fig. 4a–c. The Raman bands appearing at ~ 475.3 and 484.7 cm−1 belong to the scissoring modes of tt-BA, i.e., δ(CH2-CH2-CH3) (δ(CCC)) and δ(CH2-CH2-NH3+)

(δ(CCN)), which are associated CH3 and HN3+ stretch in opposite directions (Fig. 4a, Table S2, and the vibration modes shown in the inset of Fig. 4c). The observed characteristic band at ~

864.7 cm−1 belongs to the rocking mode of tt-BA, i.e., ρtt. Besides, there is a very weak band at ~ 837.2 cm−1 originating from the rocking of CH2 (Fig. 4b, Table S3, and the vibrational

mode shown in the inset of Fig. 4c). Upon compression at 0.2 GPa, the Raman spectrum shows distinct changes. First, the δ(CCC) and δ(CCN) bands almost merge into one band at ~ 487.2 cm−1,

which is the spectrally overlapped scissoring modes of BA in the trans-gauche and gauche-gauche form, i.e., δtg and δg+g-, respectively (Fig. 4a). Besides, the intensity of ρtt weakens

(Raman inactive-like) under compression, while the intensity of the Raman band at ~840 cm−1 is enhanced due to the formation of Raman-active tg and g+g- BA conformers (Fig. 4b). From 0.6 to

3.0 GPa, the characteristic scissoring and rocking modes of tg and g+g- BA conformers show a continuous blue shift (Supplementary Fig. 10b, c), which reflects lamellar contraction26,30.

Above 3.0 GPa, the distortion of Pb-I sublattice lowers the lattice symmetry19,20, which splits the degenerate scissoring and rocking bands of BA in tg and g+g- conformations, as

demonstrated by the Raman spectrum measured at 3.7 GPa. However, all Raman peaks becomes weak and disappears beyond 6.0 GPa due to the structural amorphization (Supplementary Fig. 10a). The

evolution of peak position and intensity of BA scissoring and rocking modes measured by the in situ Raman spectra under compression (< 3.0 GPa) evidences the bond-by-bond rotation of the

BA molecules to form distinct rotational isomers during lamellar contraction. More importantly, the irreversible changes of BA scissoring (Fig. 4d) and rocking (Fig. 4e) modes in the Raman

spectra measured after decompression further proves the formation of BA tg and g+g- conformers. Interestingly, the fingerprint of Raman bands of tg and g+g- conformers is still clear after

decompression from high-pressure amorphous state (9.8 GPa), thus the BA conformers are strain-hardened and stabilized under high-pressure treatment. At ambient conditions, the high-energy

isomers could partially transform back to the tt isomer according to the moderate barrier as shown by our DFT and AIMD simulations. This reversible isomerization renders the storage of the

mechanical energy and hindrance of the deformation. In contrast, in the case of _n_ = 1 RPP, previous high-pressure Raman study by us showed that the BA chain remains linear under

compression, and a totally reversible Raman spectrum is obtained after decompression21. This implies an interesting thickness (_n_)-selective response rooted in the _n_-dependent

isomerization of the BA molecule. BROADBAND PHOTOLUMINESCENCE SPECTRA IN THE EXFOLIATED RPP CRYSTALS The changes in excitonic absorption or emission properties of bulk hybrid perovskite

crystals under compression have been attributed to changes in bond lengths and bond angles of the inorganic octahedral cages, which affect the overlap of Pb 6 s and I 5p orbitals19,31. The

exfoliated flakes are much thinner than bulk crystal and allow compression or relaxation effects to permeate much more quickly throughout the sample compared to the bulk (Supplementary Fig. 

11), thus upon decompression, the elastic potential energy stored in the inorganic sublattice can be released quickly. By recording PL during compression-decompression, we can study the

pressure threshold of the elastic recovery regime. In addition, surface effects are strongly amplified in the mechanical exfoliated flakes29,32,33, as revealed by the pronounced PL emission

located at the low-energy side in addition to the intrinsic excitonic emission as shown in the Supplementary Fig. 1222. Figure 5a shows the PL spectra of exfoliated _n_ = 2 RPP flake with

thickness of ~ 17 nm (~ 8 layers) that are collected under compression, while Fig. 5b shows the one-to-one corresponding spectra after decompression (refer to the Supplementary Fig. 13 for

PL spectra of other two exfoliated flakes). Before compression, the sample displays a clear intrinsic excitonic emission at ~ 2.14 eV arising from the bulk-like state (BS), this corresponds

to the state where the majority of its BA molecules adopt the trans configuration typical of ground state alkane molecules. A low-energy PL emission centered at ~ 2.06 eV is related to

surface state (SS) emission introduced by a small population of relaxed/disordered tt-conformer BA molecules34. Upon compression to 2.5 GPa, the BS and SS emissions red shift continuously

and merge into a single peak at 3.9 GPa (PL peak positions vs pressure shown in the Supplementary Fig. 14). This single peak blue shifts with further increase in pressures until a drastic

drop in PL intensity occurs due to amorphization (> ~ 5.8 GPa), as shown in Fig. 5a and the Supplementary Fig. 14. Importantly, below the pressure of 2.5 GPa, the PL spectra can recover

to the initial state after decompression, as judged from the suppression of broadband emission at the low-energy side in Fig. 5b (highlighted by blue arrow). The ability of the PL to recover

is due to the elastic recovery of the Pb-I sublattice. In other words, the soft organic cation buffers the compressive strain and allows the inorganic lattice to remain in the elastic

regime without crossing the yield point. At pressure higher than 2.5 GPa, e.g., 3.9 GPa, the pressure yield point is exceeded in the stress-strain curves and the PL peak broadened

irreversibly. To elucidate the origins of the observed broadband PL emission, the optical absorption of the flake was recorded during compression-decompression cycles (Supplementary Fig. 

15). The absorption and PL peaks exhibit similar response under compression, suggesting their excitonic origins. Both peak intensities and energies recover after pressure is released from

3.9 GPa to atmospheric pressure, while both absorption and PL peaks becomes weak and almost disappear at 3.9 GPa. Based on the above pressure-induced response, we infer that the broadband PL

is associated with the radiative emission of the self-trapped excitons35,36. The corresponding optical photographs and fluorescence micrographs before and after compression are shown in

Fig. 5c, we can observe that emission is changed from original red color to orange. In the case of _n_ = 1, the linear BA tilting along with the octahedral tilting in the out-of-plane

direction works synergistically to accommodate elastic deformation, as demonstrated by the robust PL for _n_ = 1 RPP even at 9.9 GPa (Supplementary Fig. 16a) and the recoverable PL after

decompression (Supplementary Fig. 16b). DISCUSSION The role of the organic cations in buffering stress becomes clear when we examine the deformation resistance of the inorganic lattice for

_n_ = 1 and _n_ = 2 RPP. As _n_ increases, the ratio of the number of layers of inorganic slab (hard) to organic slab (soft) increases in the RPP homologous series from _n_ = 1 to 4, and

varying bands of tensile and compressive stress develop respectively. When the proportion of BA organic fraction decreases, the ability to buffer compressive stress in the hybrid system

decreases. As a result, there is increasing strain in the Pb-I inorganic lattice, leading to an increasingly lower pressure threshold from _n_ = 1 to 4 RPPs for permanent deformation, as

demonstrated by the in situ compression-decompression PL spectra shown in the Supplementary Fig. 16. The pressure threshold is reflected by the occurrence of non-recoverable PL after

decompression for _n_ = 1 to 4 RPPs, as summarized in Fig. 5d. As _n_ increases, the critical pressure point, above which irreversible deformation occurs, decreases, i.e., it requires a

lower compressive stress to deform the inorganic lattice, as judged by the appearance of the broadband PL. This clearly corroborates the fact that the organic cation helps to buffer the

stress during compression. Therefore, when the proportion of organic cations is increasingly diluted by thicker inorganic slab, the deformation resistance decreases. In _n_ = 1 RPP, the

compressive stress is first accommodated by the tilting of the organic cation, and this acts in concert with the in-plane slip of the inorganic slab, which results in phase change of the

crystal upon compression. The absence of methyl ammonium ions occupying the cubo-octahedral site in _n_ = 1 RPP imposes less steric hindrance, and this may allow the organic chain to tilt

and un-tilt in a reversible way. By contrast, the compressive stress in _n_ = 2 RPPs is accommodated firstly by the rotational isomerism of the organic cations. The rotation to high energy

conformer is accompanied by the in-plane tensile strain along _a_ and _b_ axis. Following decompression, elastic recovery of the inorganic octahedral cages in _n_ > 1 can be achieved, but

the pressure threshold for irreversible deformation is much lower than the _n_ = 1 case. Our results provide the essential basis for understanding how multilayer organic-inorganic system

act synergistically under compressive stress, which may be useful for understanding the isothermal barocaloric effects in perovskites, and for engineering new types of deformation-resistant

multilayer coatings. METHODS SAMPLE PREPARATION The RPP single crystals were synthesized using three precursors: PbO, C4H9NH3I (BAI) and CH3NH3I (MAI) via a temperature-programmed

crystallization method37. For (BA)2MAPb2I7 (_n_ = 2), PbO, BAI, and MAI (1.9/1.4/1 by molar, MAI: 0.31 M) were dissolved in a concentrated mixture of HI and H3PO2 (9:1, v/v). The solution

was then heated at 110 °C while stirring for 40 min to give clear solutions. Subsequently, the solutions were quickly transferred to an oven set at 110 °C and allowed to cool slowly down to

room temperature at a rate of 3 °C h−1, in which the 2D RPP crystals crystallized. The crystals were isolated via vacuum filtration and subsequently dried under vacuum at room

temperature28,29. Thin flakes of RPPs were exfoliated by following the method developed for graphene exfoliation and transferred onto a culet of 500 µm of the diamond anvil cell in the

glovebox21. HIGH PRESSURE ENVIRONMENT REALIZATION Two identical diamond anvils with a culet of 500 µm were employed to generate pressure. A stainless-steel gasket was pre-indented to 50 µm

with a drilled hole 300 µm in diameter serving as the sample chamber. A small ruby ball was loaded together with _n_ = 2 RPP. The pressure was calibrated using the pressure-dependent ruby

fluorescent technique31. RAMAN AND PL MEASUREMENTS DURING COMPRESSION-DECOMPRESSION CYCLES Raman spectra were conducted by using Renishaw Invia Raman microscope. A solid-state 785 nm laser

was used to excite Raman scattering to avoid strong PL background as well as any sample degradation. For the high-pressure PL measurements, the bulk RPP crystals were first exfoliated on

polydimethylsiloxane (PDMS) following the method developed for graphene exfoliation38, and perovskite flakes with different thicknesses were then selected and transferred onto the pressing

surface (500 µm) of the DAC using a transfer stage. The exfoliation and transfer processes were carried out in an argon-filled glove box. The RPP microsheets were covered with a silicone oil

before taking out of the glove box for in situ PL measurements under compression and decompression. PL spectra were excited by 532 nm laser using WITec alpha 300RAS microscope.

FIRST-PRINCIPLES CALCULATIONS The structural evolutions under compression and decompression were simulated by using Vienna ab initio simulation package (VASP)39. An additional vacuum layer

of thickness greater than 15 Å was adopted. The Perdew-Burke-Ernzerhof functional for the exchange-correlation potential was used together with a kinetic energy cutoff of 500 eV and a 3×3×1

Monkhorst-Pack grid. All the structures are fully relaxed until the force on each atom is less than 0.005 eV Å−1. The van der Waal’s interactions were treated by using DFT-D3 method. The

hydrostatic model is based on the calculations and experimental results of low-dimensional materials under pressure40,41,42. More details about model construction, molecular dynamics

calculations and Raman calculation can be found in the Supplementary Discussion. DATA AVAILABILITY All data generated and analyzed in this study are included in the article and its

Supplementary Information, and are also available from authors upon request. The source data is provided with this work as a Source Data file. Source data are provided with this paper. CODE

AVAILABILITY The code supporting the findings of this study are available from the corresponding author upon request. REFERENCES * Stoumpos, C. C. et al. Ruddlesden–popper hybrid lead Iodide

perovskite 2D homologous semiconductors. _Chem. Mater._ 28, 2852–2867 (2016). Article  CAS  Google Scholar  * Mao, L., Stoumpos, C. C. & Kanatzidis, M. G. Two-dimensional hybrid halide

perovskites: principles and promises. _J. Am. Chem. Soc._ 141, 1171–1190 (2019). Article  CAS  Google Scholar  * Blancon, J.-C., Even, J., Stoumpos, C. C., Kanatzidis, M. G. & Mohite, A.

D. Semiconductor physics of organic–inorganic 2D halide perovskites. _Nat. Nanotechnol._ 15, 969–985 (2020). Article  ADS  CAS  Google Scholar  * Guo, Z., Wu, X., Zhu, T., Zhu, X. &

Huang, L. Electron–phonon scattering in atomically thin 2D perovskites. _ACS Nano_ 10, 9992–9998 (2016). Article  CAS  Google Scholar  * Zhang, F. et al. Advances in two-dimensional

organic–inorganic hybrid perovskites. _Energy Environ. Sci._ 13, 1154–1186 (2020). Article  CAS  Google Scholar  * Tsai, H. et al. Design principles for electronic charge transport in

solution-processed vertically stacked 2D perovskite quantum wells. _Nat. Commun._ 9, 2130 (2018). Article  ADS  Google Scholar  * Grancini, G. & Nazeeruddin, M. K. Dimensional tailoring

of hybrid perovskites for photovoltaics. _Nat. Rev. Mater._ 4, 4–22 (2019). Article  ADS  CAS  Google Scholar  * Dou, L. et al. Atomically thin two-dimensional organic-inorganic hybrid

perovskites. _Science_ 349, 1518–1521 (2015). Article  ADS  CAS  Google Scholar  * Gan, Z. et al. Photophysics of 2D organic–inorganic hybrid lead halide perovskites: progress, debates, and

challenges. _Adv. Sci._ 8, 2001843 (2021). Article  CAS  Google Scholar  * Chen, Y. et al. 2D ruddlesden–popper perovskites for optoelectronics. _Adv. Mater._ 30, 1703487 (2018). Article 

Google Scholar  * Mitzi, D. B. Templating and structural engineering in organic–inorganic perovskites. _J. Chem. Soc., Dalton Trans_., 1-12 (2001). * Liu, S. et al. Manipulating efficient

light emission in two-dimensional perovskite crystals by pressure-induced anisotropic deformation. _Sci. Adv._ 5, eaav9445 (2019). Article  ADS  CAS  Google Scholar  * Li, H. et al. Unusual

pressure-driven phase transformation and band renormalization in 2D vdW hybrid lead halide perovskites. _Adv. Mater._ 32, 1907364 (2020). Article  CAS  Google Scholar  * Kong, L. et al.

Highly tunable properties in pressure-treated two-dimensional dion–jacobson perovskites. _Proc. Natl Acad. Sci. U.S.A._ 117, 16121–16126 (2020). Article  ADS  CAS  Google Scholar  * Guo, S.

et al. Pressure-suppressed carrier trapping leads to enhanced emission in two-dimensional perovskite (HA)2(GA)Pb2I7. _Angew. Chem. Int. Ed. Engl._ 59, 17533–17539 (2020). Article  CAS 

Google Scholar  * Chen, Y. et al. Emission enhancement and bandgap retention of a two-dimensional mixed cation lead halide perovskite under high pressure. _J. Mater. Chem. A_ 7, 6357–6362

(2019). Article  CAS  Google Scholar  * Yuan, Y. et al. Large band gap narrowing and prolonged carrier lifetime of (C4H9NH3)2PbI4 under high pressure. _Adv. Sci._ 6, 1900240 (2019). Article

  Google Scholar  * Zhang, L., Wu, L., Wang, K. & Zou, B. Pressure-induced broadband emission of 2D organic–inorganic hybrid perovskite (C6H5C2H4NH3)2PbBr4. _Adv. Sci._ 6, 1801628

(2019). Article  Google Scholar  * Liu, G. et al. Two regimes of bandgap red shift and partial ambient retention in pressure-treated two-dimensional perovskites. _ACS Energy Lett._ 2,

2518–2524 (2017). Article  CAS  Google Scholar  * Liu, G. et al. Isothermal pressure-derived metastable states in 2D hybrid perovskites showing enduring bandgap narrowing. _Proc. Natl Acad.

Sci. USA_ 115, 8076–8081 (2018). Article  ADS  CAS  Google Scholar  * Yin, T. et al. Pressure-engineered structural and optical properties of two-dimensional (C4H9NH3)2PbI4 perovskite

exfoliated nm-thin flakes. _J. Am. Chem. Soc._ 141, 1235–1241 (2019). Article  CAS  Google Scholar  * Leng, K. et al. Molecularly thin two-dimensional hybrid perovskites with tunable

optoelectronic properties due to reversible surface relaxation. _Nat. Mater._ 17, 908–914 (2018). Article  ADS  CAS  Google Scholar  * McNulty, J. A. & Lightfoot, P. Structural chemistry

of layered lead halide perovskites containing single octahedral layers. _IUCrJ_ 8, 485–513 (2021). Article  CAS  Google Scholar  * Billing, D. G. & Lemmerer, A. Synthesis,

characterization and phase transitions in the inorganic-organic layered perovskite-type hybrids [(C_n_H2_n_+1NH3)2PbI4], _n_ = 4, 5 and 6. _Acta Cryst. B_ 63, 735–747 (2007). Article  CAS 

Google Scholar  * Marchenko, E. I. et al. Layer shift factor in layered hybrid perovskites: univocal quantitative descriptor of composition–structure–property relationships. _Chem. Mater._

33, 1213–1217 (2021). Article  CAS  Google Scholar  * Yin, T. et al. Hydrogen-bonding evolution during the polymorphic transformations in CH3NH3PbBr3: experiment and theory. _Chem. Mater._

29, 5974–5981 (2017). Article  CAS  Google Scholar  * Martins, L. G. P. et al. Raman evidence for pressure-induced formation of diamondene. _Nat. Commun._ 8, 96 (2017). Article  ADS  Google

Scholar  * Abdelwahab, I. et al. Highly enhanced third-harmonic generation in 2D perovskites at excitonic resonances. _ACS Nano_ 12, 644–650 (2018). Article  CAS  Google Scholar  * Leng, K.,

Fu, W., Liu, Y., Chhowalla, M. & Loh, K. P. From bulk to molecularly thin hybrid perovskites. _Nat. Rev. Mater._ 5, 482–500 (2020). Article  ADS  CAS  Google Scholar  * Chang, H. C.,

Jiang, J. C., Su, J. C., Chang, C. Y. & Lin, S. H. Evidence of rotational isomerism in 1-butyl-3-methylimidazolium halides: a combined high-pressure infrared and Raman spectroscopic

study. _J. Phys. Chem. A_ 111, 9201–9206 (2007). Article  CAS  Google Scholar  * Yin, T. et al. High-pressure-induced comminution and recrystallization of CH3NH3PbBr3 nanocrystals as large

thin nanoplates. _Adv. Mater._ 30, 1705017 (2018). Article  Google Scholar  * Shi, E. et al. Extrinsic and dynamic edge states of two-dimensional lead halide perovskites. _ACS Nano_ 13,

1635–1644 (2019). Article  CAS  Google Scholar  * Kepenekian, M. et al. Concept of lattice mismatch and emergence of surface states in two-dimensional hybrid perovskite quantum wells. _Nano

Lett._ 18, 5603–5609 (2018). Article  ADS  CAS  Google Scholar  * Shao, Y. et al. Unlocking surface octahedral tilt in two-dimensional Ruddlesden-Popper perovskites. _Nat. Commun._ 13, 138

(2022). Article  ADS  CAS  Google Scholar  * Ma, Z. et al. Pressure-induced emission of cesium lead halide perovskite nanocrystals. _Nat. Commun._ 9, 4506 (2018). Article  ADS  Google

Scholar  * Shi, Y. et al. Pressure-induced emission (PIE) of one-dimensional organic tin bromide perovskites. _J. Am. Chem. Soc._ 141, 6504–6508 (2019). Article  CAS  Google Scholar  *

Mitzi, D. B. Synthesis, crystal structure, and optical and thermal properties of (C4H9NH3)2MI4 (M = Ge, Sn, Pb). _Chem. Mater._ 8, 791–800 (1996). Article  CAS  Google Scholar  *

Castellanos-Gomez, A. et al. Deterministic transfer of two-dimensional materials by all-dry viscoelastic stamping. _2D Mater._ 1, 011002 (2014). Article  CAS  Google Scholar  * Kresse, G.

& Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. _Phys. Rev. B_ 54, 11169–11186 (1996). Article  ADS  CAS  Google

Scholar  * Gao, Y. et al. Ultrahard carbon film from epitaxial two-layer graphene. _Nat. Nanotechnol._ 13, 133–138 (2018). Article  ADS  CAS  Google Scholar  * Vasu, K. S. et al. Van der

Waals pressure and its effect on trapped interlayer molecules. _Nat. Commun._ 7, 12168 (2016). Article  ADS  CAS  Google Scholar  * Tiwari, S. K. et al. Progress in diamanes and diamanoids

nanosystems for emerging technologies. _Adv. Sci._ 9, e2105770 (2022). Article  Google Scholar  Download references ACKNOWLEDGEMENTS K.P.L. wishes to acknowledge grant P0043087 of Hong Kong

Polytechnic University. T.Y. gratefully acknowledges strong support from the Presidential Postdoctoral Fellowship of Nanyang Technological University. T.Y. and H.S. would like to acknowledge

the support from the Singapore National Research Foundation via Competitive Research Programme (NRF-CRP21-2018-0007 and NRF-CRP23-2019-0007). Z.S. and L.Y. would like to acknowledge the MOE

Tier 2 MOE-T2EP50220-0020 and MOE Tier 1 RG57/21 and RG156/19 (S). K.L. would like to acknowledge the Research Grants Council of the Hong Kong Special Administrative Region, China (Project

No. PolyU15305221 for GRF project funded in 2021/22 Exercise). Y.C. would like to acknowledge the University of Macau (SRG2019-00179-IAPME, MYRG2020-00075-IAPME) and the Science and

Technology Development Fund from Macau SAR (FDCT-0163/2019/A3), the Natural Science Foundation of China (Grant 22022309) and Natural Science Foundation of Guangdong Province, China

(2021A1515010024). This work was performed in part at the High-Performance Computing Cluster (HPCC), which is supported by the Information and Communication Technology Office (ICTO) of the

University of Macau. AUTHOR INFORMATION Author notes * These authors contributed equally: Tingting Yin, Hejin Yan. AUTHORS AND AFFILIATIONS * Division of Physics and Applied Physics, School

of Physical and Mathematical Sciences, Nanyang Technological University, Singapore, 637371, Singapore Tingting Yin, Yulia Lekina, Handong Sun & Ze Xiang Shen * Joint Key Laboratory of

Ministry of Education Institute of Applied Physics and Materials Engineering, University of Macau, Macau, China Hejin Yan & Yongqing Cai * Department of Chemistry, National University of

Singapore, Singapore, 117543, Singapore Ibrahim Abdelwahab & Kian Ping Loh * Centre for Disruptive Photonic Technologies, the Photonics Institute, Nanyang Technological University,

Singapore, 637371, Singapore Yulia Lekina & Ze Xiang Shen * Center for High Pressure Science and Technology Advanced Research, (HPSTAR), Shanghai, 201203, P.R. China Xujie Lü & Wenge

Yang * Department of Applied Physics, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong, China Kai Leng & Kian Ping Loh Authors * Tingting Yin View author publications

You can also search for this author inPubMed Google Scholar * Hejin Yan View author publications You can also search for this author inPubMed Google Scholar * Ibrahim Abdelwahab View author

publications You can also search for this author inPubMed Google Scholar * Yulia Lekina View author publications You can also search for this author inPubMed Google Scholar * Xujie Lü View

author publications You can also search for this author inPubMed Google Scholar * Wenge Yang View author publications You can also search for this author inPubMed Google Scholar * Handong

Sun View author publications You can also search for this author inPubMed Google Scholar * Kai Leng View author publications You can also search for this author inPubMed Google Scholar *

Yongqing Cai View author publications You can also search for this author inPubMed Google Scholar * Ze Xiang Shen View author publications You can also search for this author inPubMed Google

Scholar * Kian Ping Loh View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS T.Y. and K.P.L. conceived the idea and designed the experiments.

T.Y. performed the high-pressure photoluminescence and Raman measurements. I.A. prepared the exfoliated ultrathin layered RPP samples in an argon-filled glovebox via micromechanical cleavage

and 2D dry transfer and performed AFM analysis. Y.L. prepared the high-pressure Raman samples. K.L. synthesized the RPP crystals. H.Y. and Y.C. performed DFT calculations. T.Y., Y.C., Z.S.,

and K.P.L. analyzed the data. T.Y. and K.P.L. wrote the manuscript. X.L., W.Y., and H.S. revised the paper. All authors contributed to finalize the manuscript. CORRESPONDING AUTHORS

Correspondence to Tingting Yin, Yongqing Cai, Ze Xiang Shen or Kian Ping Loh. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW

INFORMATION _Nature Communications_ thanks Rafael Del Grande and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. ADDITIONAL INFORMATION PUBLISHER’S

NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION SOURCE DATA

SOURCE DATA RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution

and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if

changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the

material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to

obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS

ARTICLE Yin, T., Yan, H., Abdelwahab, I. _et al._ Pressure driven rotational isomerism in 2D hybrid perovskites. _Nat Commun_ 14, 411 (2023). https://doi.org/10.1038/s41467-023-36032-y

Download citation * Received: 25 February 2022 * Accepted: 11 January 2023 * Published: 25 January 2023 * DOI: https://doi.org/10.1038/s41467-023-36032-y SHARE THIS ARTICLE Anyone you share

the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer

Nature SharedIt content-sharing initiative