Dislocation exhaustion and ultra-hardening of nanograined metals by phase transformation at grain boundaries

ABSTRACT The development of high-strength metals has driven the endeavor of pushing the limit of grain size (d) reduction according to the Hall-Petch law. But the continuous grain refinement

is particularly challenging, raising also the problem of inverse Hall-Petch effect. Here, we show that the nanograined metals (NMs) with d of tens of nanometers could be strengthened to the

level comparable to or even beyond that of the extremely-fine NMs (d ~ 5 nm) attributing to the dislocation exhaustion. We design the Fe-Ni NM with intergranular Ni enrichment. The results

show triggering of structural transformation at grain boundaries (GBs) at low temperature, which consumes lattice dislocations significantly. Therefore, the plasticity in the

dislocation-exhausted NMs is suggested to be dominated by the activation of GB dislocation sources, leading to the ultra-hardening effect. This approach demonstrates a new pathway to explore

NMs with desired properties by tailoring phase transformations via GB physico-chemical engineering. SIMILAR CONTENT BEING VIEWED BY OTHERS THE ORIGIN OF EXCEPTIONALLY LARGE DUCTILITY IN

MOLYBDENUM ALLOYS DISPERSED WITH IRREGULAR-SHAPED LA2O3 NANO-PARTICLES Article Open access 15 May 2024 NEAR-THEORETICAL STRENGTH AND DEFORMATION STABILIZATION ACHIEVED VIA GRAIN BOUNDARY

SEGREGATION AND NANO-CLUSTERING OF SOLUTES Article Open access 28 October 2024 IN SITU ATOMIC-SCALE OBSERVATION OF DISLOCATION CLIMB AND GRAIN BOUNDARY EVOLUTION IN NANOSTRUCTURED METAL

Article Open access 18 July 2022 INTRODUCTION Grain refinement is one of the prevailing strengthening methods as depicted by the Hall–Petch relationship1,2: the strength is inversely

proportional to the square root of grain size (d). The pursuit of high-strength metals has led to the development of numerous strategies to push the limit of grain refinement3,4,5. However,

the extension of the grain-size strengthening to the size range below 10–15 nm is restricted either by the challenges in materials generation6 or by the inverse Hall–Petch effect7,8,9,10.

These challenges are closely related to the size dependence of deformation mechanisms of nanograined metals (NMs). In the grain size range where the Hall–Petch law works, the plastic

deformation is determined by the dislocation mechanism. Under mechanical loading, dislocation sources are activated and the glide of lattice dislocations provides the carriers for plastic

strain. But when the grain size is further reduced to the so-called extremely-fine nanograined regime with d of a few nanometers, it is suggested that the grain boundary (GB) processes,

e.g., GB sliding and GB migration or coupling9,10,11, become dominant in plasticity, which contributes to the observed inverse Hall–Petch effect. Accessing the strength limit of NMs drives

one to explore pathways to tailor the behavior of GBs and dislocations, instead of focusing on the grain size alone. Inspiration is provided by the recently-reported annealing-induced

hardening11,12,13,14,15, which is usually attributed to the GB stabilization by relaxation or segregation. However, for the NMs where the plasticity is clearly mediated by the glide of

pre-existing lattice dislocations, the hardening due to the annihilation of such dislocations by annealing is also observed but to a much lesser extent14. The potential of strengthening by

wiping out lattice dislocations in NMs by annealing is generally limited by the occurrence of significant grain growth, which leads to a net softening of the material. Thus, a question of

both fundamental and technological interests arises if design strategies can be devised to create a nanostructure with dislocation-free grain interiors and with GBs that are immobilized and

hardened against premature activation of dislocation motion. For that reason, a specific thermo-mechanical processing pathway has been designed to tune the local atomic and chemical

structure of the grain interiors and the GBs in a NM. A structural transformation at GBs, which is triggered by low-temperature annealing, exhausts the residual lattice dislocations but

avoids significant grain growth. These structural changes could result in the formation of dislocation-exhausted grains and in a transition of plasticity from being dominated by the glide of

pre-existing lattice dislocations to being controlled by dislocation nucleation at GBs, which induces an ultra-hardening effect. Considering the rich potential given by different

combinations of host alloys and GB-mediated transformations, the present study demonstrates a versatile pathway to explore uncharted regions of mechanical properties of NMs. RESULTS

NANOSTRUCTURE AND MECHANICAL PROPERTY We have prepared a nanograined Fe84Ni16 (at%) alloy by using the technique of Inert Gas Condensation (IGC). The IGC samples consist of equiaxed

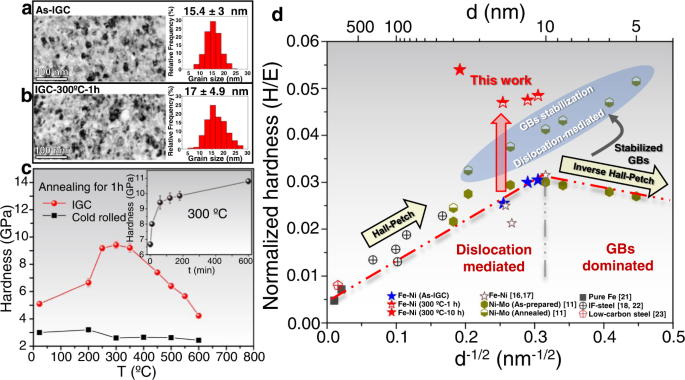
nano-sized grains (15.4 ± 3 nm) as shown in Fig. 1a and exclusively of the BCC phase as detected by XRD and TEM (Supplementary Fig. 1). The IGC nanograined Fe-Ni sample exhibits a

microhardness of 5.1 ± 0.2 GPa, which agrees with the reported values for iron and iron alloys of similar grain size16,17,18. Surprisingly, the hardness is dramatically increased upon

low-temperature annealing, and the comparison in Fig. 1c shows a peak hardness of 9.4 ± 0.3 GPa by annealing at 300 °C for 1 h. No obvious grain growth is observed after such annealing as

shown in Fig. 1b. Annealing at higher temperatures results in a softening trend, which goes along with extensive grain growth (Supplementary Fig. 2). Longer annealing duration of the

nanograined Fe-Ni alloy at 300 °C shows an even increasing hardness, reaching 10.8 ± 0.2 GPa for 10 h (insert in Fig. 1c). In contrast, annealing-induced hardening was not observed for the

same alloy with ultrafine-grained (UFG) microstructure obtained by cold rolling. Although the indentation hardness value is correlated to the flow stress at certain plastic strain19, this

technique has been widely used in characterizing the mechanical properties of NMs, and provides a proper ranking of the strength level3,11,20. Considering the lack of strain hardening of

NMs, the hardness value is regarded as representing the magnitude of yield strength. The comparison in Fig. 1d clearly highlights the effect of annealing on the IGC Fe-Ni alloy. Firstly, the

as-prepared IGC samples present hardness values that fall in line with the Hall–Petch plot of the Fe-based alloys, and the inverse Hall–Petch effect is not observed. This suggests a

dislocation-mediated, rather than GB-dominated, plastic deformation, which is also substantiated by the absence of obvious grain growth and grain structure changes in the deformed

microstructure underneath the microindents (Supplementary Figs. 3 and 4). Secondly, the hardening efficiency of the IGC Fe-Ni alloy due to annealing has not been achieved in other NMs with

_d_ > 10 nm (Supplementary Fig. 5). Significant annealing-induced hardening was also reported for the electrodeposited extremely-fine nanograined Ni-Mo alloys with _d_ < 10 nm, but the

deformation of these alloys is controlled by GB-dominated mechanism that leads to the inverse Hall–Petch effect11. Therefore, the present results show a higher hardening effect due to

annealing when comparing with other NMs that involve also dislocation-mediated deformation. Furthermore, the IGC-annealed (300 °C for 10 h) Fe-Ni sample with _d_ = 27 ± 7 nm (Supplementary

Fig. 6) was even strengthened beyond the level of the extremely-fine NMs (_d_~5 nm), as highlighted in Fig. 1d. STRUCTURAL AND CHEMICAL ANALYSIS We have performed a systematic

characterization campaign by using multiple techniques to reveal the structural and chemical processes during the annealing treatment. The density measurements demonstrate that the initial

density of as-IGC nanograined Fe-Ni alloy is ~97% of the as-cast sample, and no measurable densification occurs during annealing. An exothermic peak is detected between 100 °C and 200 °C in

the DSC curve with an excess energy of 675.8 J/mol (Supplementary Fig. 7), which is comparable to the measurements in refs. 24,25. The relaxation at this stage is probably responsible for

the hardness increment from 5.1 GPa to 6.2 GPa by annealing up to 200 °C. Subsequently, atom probe tomography was conducted for the as-prepared IGC and annealed (300 °C for 1 h) nanograined

Fe-Ni samples, respectively. Trace impurities (carbon, oxygen, and nitrogen) with a total content of ~0.7 at% are found distributing uniformly in the IGC sample and kept unchanged after

annealing (Supplementary Fig. 8), which indicates a negligible effect on the annealing-induced ultra-hardening phenomenon. However, the distribution of Ni in the IGC sample is heterogeneous,

involving a network-type enrichment and a wavelength comparable to the grain size (Fig. 2a), which is in contrast with the homogeneous distribution of Ni in the cold-rolled UFG Fe-Ni alloy

(Supplementary Fig. 9). The local enrichment of Ni has been found to reach a level of 24 at%. This intergranular Ni enrichment is probably generated during the formation of nanoclusters in

the IGC synthesis. Upon annealing, the chemical heterogeneity is enhanced in terms of the size and concentration of the Ni-enriched regions (Fig. 2b). Quantitative analysis of the annealed

sample (Fig. 2c) shows that the local Ni concentration increases to 40–50 at%, with a typical size of the regions from a few nm to 15 nm. Additional TEM-EDX mapping also shows the

intergranular Ni enrichment, especially at the triple junctions (Supplementary Fig. 10). The structural changes are investigated by using in-situ synchrotron X-ray diffraction (XRD) during

the annealing of the IGC nanograined Fe-Ni alloy (heating to 300 °C and holding for 1 h). Figure 3a and b shows the evolution of the diffractograms, clearly indicating that the single-phase

BCC structure is maintained up to 300 °C for short annealing time. During the isothermal annealing, a BCC-FCC transformation occurs, with a content of the FCC phase of 2 vol% at 10 min and 8

 vol% at 60 min. Therefore, during annealing, the concurrence of the isothermal BCC-FCC structural change and the diffusion process of Ni re-distribution were observed. The formation of a

new phase with a different composition to the matrix suggests that diffusion, most probably along the GB network, plays an important role in the observed structural transformation26. Note

that 300 °C is a rather low homologous temperature (~0.33_T_m) for iron. In addition, there is a lack of chemical driving force in Fe–Ni alloy with this nominal composition (Supplementary

Fig. 11a). Actually, a much higher FCC-forming temperature (580 °C) is found in the cold-rolled UFG counterpart (Supplementary Fig. 11b). However, the unique structural and chemical features

of the IGC nanograined alloy facilitate the onset of the transformation. Firstly, the local Ni enrichment tends to increase the thermodynamic driving force27 and favor the formation of FCC

phase by decreasing the BCC-FCC transformation temperature (Supplementary Fig. 11a). Secondly, the enhanced diffusivity due to the high density of high-angle GBs kinetically facilitates the

transformation processes28. Assuming the width of GBs to be 0.5 nm, the GB diffusion distance of Ni in BCC Fe at 300 °C for 1 h is estimated as 22 nm29,30,31, which is a value comparable to

the grain size. Thirdly, the local compressive strain field at the GB regions, as revealed by the geometrical phase analysis in Supplementary Fig. 12, could help accommodate the volume

shrinkage during the BCC-FCC transformation and provide additional internal mechanical driving force32,33. The diffraction profile analysis provides the critical structural parameters,

including the average grain size and the magnitude of micro-strain distribution, according to the modified Williamson–Hall method34. The details of the profile analysis can be found in

Supplementary Fig. 13, and the results of the analysis are listed in Supplementary Table 1. As shown in Fig. 3d, a high initial density of lattice dislocations is observed in the as-prepared

IGC state (1.2 × 1015 m−2), which decreases during annealing. After annealing at 300 °C for 1 h, the dislocation density is substantially reduced to 4.1 × 1013 m−2. A salient increase in

hardness is observed accompanied with the decrease of dislocation density. The structural changes occurring during annealing are examined in detail using HR-TEM. In the IGC sample, we

clearly observe dislocations adjacent to the GBs as shown in Fig. 4a. Occasionally, dislocations are also observed that are located in the center of the grains (Supplementary Fig. 14a). In

addition, the GPA results show that the lattice dislocations are also inducing a long-range stress field (Supplementary Fig. 12)32,33. Besides the edge dislocations revealed directly by

HR-TEM, the rigid body rotation also indicates the presence of screw dislocations (Supplementary Fig. 12). In the annealed sample, the dislocation annihilation creates the

dislocation-exhausted BCC nanograins, a typical example being shown in Fig. 4b. The FCC phase with a size of ~5 nm nucleated at the GBs. The observed significant decrease in dislocation

density and the structural transformation are consistent with the synchrotron diffraction results. When deforming the annealed sample, significant dislocation storage occurs (as shown in

Supplementary Fig. 14b), which again suggests the occurrence of dislocation-mediated plastic deformation processes in the present nanograined system. For dislocation-mediated plasticity in

NMs, it is usually assumed that the grain interior is free of dislocations, and dislocations are nucleated at the GB, slipping through the entire grain and being absorbed by the GB on the

opposite side of the grain35,36,37,38. However, the pre-existence and storage of dislocations in nanograins are issues under debate, and the dislocation-free assumption in the above physical

picture has been challenged by a series of studies using X-ray line profile analysis and/or HR-TEM15,39,40. The significant peak broadening in the diffraction patterns of the nanograined

alloy is not only caused by the very small grain size but also by the inhomogeneous internal elastic strains due to the existence of lattice dislocations. Note that only dislocations

remaining in the lattice cause the long-range stress fields, which is clearly shown in Supplementary Fig. 12, and induce peak broadening, while dislocations absorbed in the GBs are not

associated with such long-range stress fields39. In the as-prepared IGC samples, the dislocation density of the order of 1015 m−2 is comparable to the reported magnitude in other NMs

prepared by severe plastic deformation40,41. In the IGC samples, dislocations are located near the GBs as shown in Fig. 4a. Such lattice dislocations attached to GBs can be activated under

the applied stress and consequently accommodate plastic deformation. After annealing at 300 °C, the dislocation density is reduced by two orders of magnitude to ~1013 m−2, close to the level

of well-annealed metals42. In severely-deformed metals, such magnitude of dislocation annihilation can only be achieved by annealing at a high homologous temperature42. The above

measurements suggest that the lattice dislocations in the present nanograins are exhausted by annealing, and alternative dislocation sources have to be activated at the GBs, which requires a

higher stress and induces the dramatic hardening observed in the present study. To elucidate the significance of the GB-mediated transformation, we establish the linkage between phase

transformation, dislocation density, and hardness as shown in Supplementary Table 1. During the heating period from RT to 300 °C without phase transformation, the dislocation density

decreases from 1.2 × 1015 m−2 to 2.0 × 1014 m−2 (83% reduction) associated with a hardness increase from 5.1 GPa to 6.7 GPa (31% increment). The larger hardness increase of 53% (from 6.7 GPa

to 9.4 GPa) is associated with the phase transformation during the holding stage, accompanied by an additional 13% reduction of the dislocation density from 2.0 × 1014 m−2 to 4.1 × 1013 

m−2. Although the phase transformation does not result in a sharp decrease of the dislocation density in an absolute sense, it does change the nature of the dislocation structure in the

grains, i.e., by wiping out the residual lattice dislocations to a very low level. The significance of the residual lattice dislocations can be highlighted by the estimation that the

sweeping of a single dislocation in a nanograin with _d_~15 nm can produce a plastic shear of the order of _b_/_d_ (~1.6%)43. When the intragranular dislocation sources were exhausted after

the occurrence of phase transformation, the dislocation activation becomes controlled by GB sources. DISCUSSION The IGC nanograined Fe-Ni alloy involves a grain size of ~15 nm, which is

within the grain size regime where the Hall–Petch law works, without involving the inverse Hall–Petch effect. The absence of stress-driven grain growth was evidenced, indicating that the GB

migration is not a significant deformation mechanism. These experimental observations demonstrate a dislocation-mediated deformation mechanism. A high density of pre-existing lattice

dislocations was identified by the XRD profile analysis. And the ultra-hardening is suggested to be attributed to the dramatic reduction of lattice dislocation density via phase

transformation at GBs during annealing. The mechanism of dislocation exhaustion by such a structural transformation can be explained as follows: In the nanograined structure produced by the

IGC process, the lattice dislocations attached to the GBs are enhancing the local internal energy through the contribution of strain energy. In addition, the lattice dislocations at the GB

region are presumably increasing the diffusivity. Thus, the locations of GBs with attaching dislocations provide the favored nucleation sites for the structural transformation. In return,

the transformation events consume such lattice dislocations attaching to the GBs. In addition, the transformation involves a flux of diffusing species (vacancies, atoms), which could

accelerate the annihilation of the residual lattice dislocations by, e.g., dislocation climb. These effects are suggested to facilitate the formation of a dislocation-exhausted nanograined

structure. Since the small FCC islands are formed at the GBs of the BCC matrix, they are not reducing the mean free path of dislocation glide as in the case of precipitation hardening. In

addition, the FCC second phase is not expected to be responsible for such ultra-hardening effect through the composite strengthening mechanism. If we estimate the hardness of the second

phase according to the rule of mixtures, a value of 55 GPa is obtained, which is too high for a metallic phase constituent. We have also prepared a FCC Fe50Ni50 nanograined sample (grain

size: 21 ± 5.5 nm) by IGC (see Supplementary Fig. 15) and obtained a hardness of 4.2 GPa, which is lower than the hardness of the BCC Fe84Ni16 sample and is thus not supposed to act as a

reinforcement. In order to experimentally substantiate the proposed GB-mediated transformation strengthening pathway, we prepared a nanograined Pd-Au alloy with _d_ = 19.2 ± 6 nm using IGC,

which is a solid solution without phase transformation during annealing. In this case, we observe a moderate hardening of 0.75 GPa (Δ_H_V/_H_V0 = 17.6%) by annealing when compared with the

as-prepared IGC state, which is induced by mechanisms other than phase transformation (Supplementary Fig. 16). It should be noted that the ultra-hardening effect observed here is also

attributed to the moderate stability of grain size, since significant grain growth could counteract and overwhelm the strengthening contributions. The grain size of 15 nm was maintained

during the annealing at 300 °C for 1 h, while annealing at a higher temperature (e.g., 500 °C) results in an increased grain size (~90 nm) and in a reduced hardness. The thermal stability of

the present nanograined Fe-Ni alloy is higher than the nanograined pure iron prepared also by IGC44. This is probably attributed to the Ni segregation and the formation of FCC phase at the

GBs during the low-temperature annealing, which pin the GB migration and retard grain growth. Note that the substitutional Ni strengthens the lattice of BCC iron45, and the Ni depletion in

the BCC phase due to the formation of Ni-rich FCC phase tends to reduce the shear resistance, which was not observed in the experiments. This observation can be rationalized as follows: when

the plastic deformation is controlled by dislocation nucleation at GBs, the strengthening due to a high defect nucleating stress will overwhelm the reduction of solid solution hardening.

The present study demonstrates that the strength of the NMs is determined not only by the grain size and GB stability, but also by the quantity of the residual lattice dislocations. When

decreasing the grain size to the nanometric scale, the intragranular dislocation sources (e.g., Frank-Read source) no longer prevail, but the residual lattice dislocations could still act as

carriers of plasticity without the necessity to excite GB dislocation sources. As mentioned before, the strengthening potential by dislocation annihilation in NMs is still experimentally

unclear15, and it is easily overwhelmed by the significant grain growth. Here, in our present approach of engineering the physicochemical characteristics of GBs in the nanograined alloys, we

can trigger the phase transformation at GBs at a low temperature to highly exhaust the residual lattice dislocations. The plastic deformation is then suggested to be dominated by the

dislocation emission from GBs, which allows for approaching the strength limit of a given nanograined polycrystal. As shown in Fig. 1d, a comparable strength can be achieved by further

reducing the grain size to the regime of extremely-fine nanometric grains (_d_~5 nm) when the GBs are stabilized, the plastic deformation of which is also controlled by dislocation emission

from GBs. In addition, when the plasticity is determined by dislocation emission from GBs, the ultra-high strength can be achieved within a range of grain size, associating with a less

stringent requirement of grain refinement. The theoretical shear strength, for either the shearing of two neighboring planes46 or the homogeneous nucleation of a dislocation47, could be

estimated as 6.6 GPa (with the order of G/10) for BCC iron. This corresponds to a Vicker’s hardness of ~60 GPa when assuming a random crystal orientation and using the empirical relationship

between strength and hardness, which is several times higher than the observed maximum hardness in this study (10.8 GPa). But the measured ultrahigh hardness is considered as approaching to

the magnitude of the theoretical limit, when accounting for the influences of the reduced elastic modulus by Ni addition and the possible stress concentrators. The as-prepared IGC

nanograined Fe-Ni alloy is initially decorated by the intergranular Ni enrichment, but the hardness is comparable to the iron alloys with similar grain sizes (Fig. 1d), which is not

suggesting the primary and direct contribution of the GB segregation to the ultra-hardening phenomenon. However, the further Ni segregation at GBs and the structural transformation during

annealing could induce other consequences. The GB structure could be changed by the phase transformation at GBs, which might influence the dislocation nucleation stress14,15,48. Since the

non-equilibrium locations at the GBs are favored sites for both the transformation and the dislocation nucleation49,50, the formation of FCC phase at such locations is increasing the

apparent dislocation nucleation stress. This effect should be more significant when the preexisting lattice dislocations are highly exhausted and when the GB characteristics dominate the

onset of plasticity, which is relevant to the continuous hardening during the prolong annealing at 300 °C (Fig. 1c). We have demonstrated a capability to control phase transformation for

development of engineering materials. It is still challenging, but promising to extend this approach to the development of nanograined materials. Controlling phase transformations in the

nanograined materials through engineering the thermodynamic and kinetic properties of GBs and interfaces, as is exemplified in this study, opens a new door to the development of

nanostructures with desired properties. METHODS SAMPLE PREPARATION The Fe-Ni nanograined alloy was synthesized by the Inert Gas Condensation (IGC) system with thermal evaporation method. The

IGC system consists of a powder preparation unit, a low-pressure compaction unit, a high-pressure compaction unit, and the base vacuum of the system is 10−6 Pa. These units are

interconnected by an ultra-high vacuum transfer line. The raw material involves a composition of Fe75Ni25. Before preparing the sample, the vacuum of the powder preparation unit was <10−6

 Pa, and then a low-pressure (500 Pa) inert gas He was introduced. The liquid nitrogen was introduced into the cold finger, and the sample was evaporated into a gaseous state by resistance

heating. The metal atoms lost energy after colliding with He gas, and deposited onto the cold finger. On the cold finger, the powder was scraped off and collected into a mold. After being

transferred to the low-pressure compaction unit, the powders are compressed into a pellet with 10 mm diameter at an applied uniaxial pressure of approx. 500 MPa. After this pre-compaction

step, the pellet was transferred to the high-pressure compaction unit where a pressure of 5 GPa was applied for 3 min at ambient temperature. Finally, we get the Fe84Ni16 nanograined alloy

with thickness of 300 μm. By adjusting the pressure of He gas (200 Pa, 50 Pa) in the preparation process, we obtained samples with smaller grain sizes. As a comparison, the sample of

Fe84Ni16 alloy was prepared by arc melting, and then was cold-rolled by 90% for the ultrafine-grained microstructure. The IGC Fe-Ni samples were annealed at modest temperatures (200 °C, 250 

°C, 300 °C, 350 °C, 450 °C, 500 °C, 550 °C, 600 °C) for 1 h (with a heating rate 20 °C/min) under the protection of an argon atmosphere. MICROHARDNESS MEASUREMENT Microhardness measurements

were performed using a Vickers microhardness tester with a load of 200 g and a dwell time of 10 s. More than ten indents were made for each condition. STRUCTURAL CHARACTERIZATION TEM and

HRTEM were conducted on a Themis Z microscope operated at 300 kV. TEM and HRTEM specimens before and after the microhardness indentation were prepared by using FEI Helios Nanolab 600i system

operated at a voltage of 30 kV to process the sample to ~1000 nm, then reduce the voltage to 16 kV and continue to thin to ~500 nm, reduce the voltage to 8 kV and continue to thin to ~200 

nm, use 5 kV to reduce to ~100 nm, and finally reduce the voltage to 2 kV and gradually reduce the thickness of the sample to ~50 nm. After thinning to the target thickness, clean the sample

with a low voltage of 1 kV to remove the amorphous layer introduced by the ion beam damage. TEM specimen of the cold-rolled Fe-Ni was mechanically ground to 50 μm in thickness, followed by

final thinning using dimpler (GrinderII, Model 657) and ion milling (PIPSII, Gatan 695). The average grain sizes were measured from the bright-field TEM images by using the Heyn intercept

method51. More than 400 grains were measured on each sample. In the measurement of grain size distribution, the grains for the FCC and BCC phases were not distinguished. The IGC Fe-Ni alloy

was characterized by using the in-situ synchrotron high-energy X-ray diffraction at beamline 11-ID-C at the Advanced Photon Source, Argonne National Laboratory. High-energy monochromatic

X-rays with a beam size of 500 μm × 500 μm and a wavelength of 0.1173 Å were used in transmission geometry for data collection. The sample was heated from room temperature to 300 °C at a

rate of 20 °C/min and then kept at 300 °C for 1 h. CHEMICAL ANALYSIS The chemical compositions of the IGC Fe-Ni samples were determined by the energy dispersive spectroscopy on a Quant

250FEG operated at 15 kV. Specimens for APT were prepared on a FEI strata FIB. The APT experiments were conducted on a Cameca LEAP 4000 XHR. The APT data reconstruction and post-processing

was done with the commercial software IVAS 3.8.452. DIFFERENTIAL SCANNING CALORIMETER MEASUREMENT Differential scanning calorimeter (DSC) measurements were performed with a Mettler Toledo

DSC1. Approximately 20 mg of samples were sealed in Al pans and scanned at a heating rate of 20 °C/min from room temperature to 300 °C. An empty Al pans was tested under the same conditions

in order to determine the baseline. DETERMINATION OF PHASE TRANSFORMATION OF COLD-ROLLED FE-NI Thermal standard expansion measurements were conducted in the compression mode using NETZSCH

402F3 thermal mechanical analyzer. A constant pre-set load of 10 mN was applied on the samples during the entire measurement. The samples were protected by the nitrogen flow with 20 ml/min,

and the temperature ranges from 27 °C to 800 °C. MEASUREMENT OF DISLOCATION DENSITY The modified Williamson–Hall (MWH) method was used for analyzing the X-ray diffraction line broadening and

measuring the dislocation density. The full widths at half maximum (FWHM) of the diffraction profiles are determined as the widths of Gaussian and Cauchy functions fitted to the

experimental diffraction data53. Instrumental broadening is calibrated based on the values of FWHM of the standard sample (CeO2). For MWH method, the FWHM of diffraction peak profiles are

plotted versus \(K{\bar{{C}}}^{1/2}\) as given by refs. 34,54: $$\varDelta {{{\rm{K}}}}=0.9/D+{(\uppi {A}^{2}{{b}}^{2}/2)}^{1/2}{\rho

}^{1/2}(K{\bar{{C}}}^{1/2})+O{(K{\bar{{C}}}^{1/2})}^{2}$$ (1) where _D_ and _K_ represent the apparent size parameters and the diffraction vector (_K_ = 2sin_θ_/_λ_, _θ_ is the Bragg angle,

Δ_K_ = 2Δ_θ_cos_θ_/_λ_ and _λ_ is the X-ray wavelength). \(\bar{{C}}\) (Table 1) is the average contrast factor of dislocations, and _O_ is a higher order term of \(K{\bar{{C}}}^{1/2}\). _A_

is constant depending on the outer cut-off radius of dislocations, _b_ is the Burgers vector of dislocations. In a polycrystalline cubic metal, the average values of the contrast factors

are calculated by55: $$\bar{{C}}={\bar{{C}}}_{{{{\rm{h00}}}}}(1-{q}{H}^{2})$$ (2) where \({\bar{{C}}}_{{{{\rm{h00}}}}}\) is a constant depending on the anisotropic elastic constants C11, C12

and C44, _q_ is a dislocation parameter recognizing relative fractions of screw and edge type dislocations56. For a given (_hkl_) reflection, _H_2 is determined by55:

$${H}^{2}=({h}^{2}{k}^{2}+{k}^{2}{l}^{2}+{l}^{2}{h}^{2})/({h}^{2}+{k}^{2}+{l}^{2})$$ (3) The value of _d_ and _ρ_1/2 can be determined by the best linear fit between _K_ and Δ_K_. ASSESSMENT

OF THE THERMODYNAMIC PROPERTIES OF THE FE-NI ALLOY The thermodynamic properties of the Fe-Ni binary system have been established in ref. 27. The difference between the chemical free energy

of the FCC and BCC phases in Fe-Ni binary alloys can be expressed as: $$\varDelta {F}^{{{{\rm{BCC}}}}{\to} FCC} =(1-{{{\rm{x}}}})(1202-2.63 \times {10}^{-3}{T}^{2}+1.54 \times

{10}^{-6}{T}^{3})+{{{\rm{x}}}}(-3700+7.09 \\ \times \,{10}^{-4}{T}^{2}+3.91 \times {10}^{-7}{T}^{3})+{{{\rm{x}}}}(1-{{{\rm{x}}}})[3600+0.58(1-\,

{{\mathrm{ln}}}\,T)]({{{\rm{cal}}}}/{{{\rm{mol}}}})$$ (4) where _x_ is the atomic fraction of Ni and _T_ is the absolute temperature. Thus, _T_0 temperature can be determined when

\(\varDelta {F}^{{{{\rm{BCC}}}}\to FCC}\)equals to zero. And the chemical driving force for the BCC-FCC structural change at a given temperature beyond _T_0 can also be provided. DATA

AVAILABILITY The data that support the findings of this study are available from the corresponding author upon request. Source data are provided with this paper. CHANGE HISTORY * _ 07

OCTOBER 2022 A Correction to this paper has been published: https://doi.org/10.1038/s41467-022-33775-y _ REFERENCES * Hall, E. O. The deformation and ageing of mild steel: III discussion of

results. _Proc. Phys. Soc. Lond. B_ 64, 747–752 (1951). Article  ADS  Google Scholar  * Petch, N. J. The cleavage strength of polycrystals. _J. Iron Steel Inst._ 174, 25–28 (1953). CAS 

Google Scholar  * Meyers, M. A., Mishra, A. & Benson, D. J. Mechanical properties of nanocrystalline materials. _Prog. Mater. Sci._ 51, 427–556 (2006). Article  CAS  Google Scholar  *

Valiev, R. Z., Islamgaliev, R. K. & Alexandrov, I. V. Bulk nanostructured materials from severe plastic deformation. _Prog. Mater. Sci._ 45, 103–189 (2000). Article  CAS  Google Scholar

  * Gleiter, H. Nanocrystalline material. _Prog. Mater. Sci._ 33, 223–315 (1989). Article  CAS  Google Scholar  * Pippan, R. et al. Saturation of fragmentation during severe plastic

deformation. _Annu. Rev. Mater. Sci._ 40, 319–343 (2010). Article  ADS  CAS  Google Scholar  * Carlton, C. E. & Ferreira, P. J. What is behind the inverse Hall–Petch effect in

nanocrystalline materials? _Acta Mater._ 55, 3749–3756 (2007). Article  ADS  CAS  Google Scholar  * Shan, Z. et al. Grain boundary-mediated plasticity in nanocrystalline nickel. _Science_

305, 654–657 (2004). Article  ADS  CAS  PubMed  Google Scholar  * Rupert, T. J., Gianola, D. S., Gan, Y. & Hemker, K. J. Experimental observations of stress-driven grain boundary

migration. _Science_ 326, 1686–1690 (2009). Article  ADS  CAS  PubMed  Google Scholar  * Schiøtz, J. & Jacobsen, K. W. A maximum in the strength of nanocrystalline copper. _Science_ 301,

1357–1359 (2003). Article  ADS  PubMed  Google Scholar  * Hu, J., Shi, Y. N., Sauvage, X., Sha, G. & Lu, K. Grain boundary stability governs hardening and softening in extremely fine

nanograined metals. _Science_ 355, 1292–1296 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Rupert, T. J., Trelewicz, J. R. & Schuh, C. A. Grain boundary relaxation strengthening

of nanocrystalline Ni–W alloys. _J. Mater. Res._ 27, 1285–1294 (2012). Article  ADS  CAS  Google Scholar  * Renk, O. et al. Increasing the strength of nanocrystalline steels by annealing: is

segregation necessary? _Scr. Mater._ 95, 27–30 (2015). Article  CAS  PubMed  PubMed Central  Google Scholar  * Huang, X., Hansen, N. & Tsuji, N. Hardening by annealing and softening by

deformation in nanostructured metals. _Science_ 312, 249–251 (2006). Article  ADS  CAS  PubMed  Google Scholar  * Ma, E., Shen, T. D. & Wu, X. L. Less is more. _Nat. Mater._ 5, 515–516

(2006). Article  ADS  CAS  PubMed  Google Scholar  * Matsui, I. et al. Enhancement in mechanical properties of bulk nanocrystalline Fe–Ni alloys electrodeposited using propionic acid.

_Mater. Sci. Eng. A_ 607, 505–510 (2014). Article  CAS  Google Scholar  * Mccrea, J. L., Palumbo, G., Hibbard, G. D. & Erb, U. Properties and applications for electrodeposited

nanocrystalline Fe-Ni Alloys. _Rev. Adv. Mater. Sci._ 5, 252–258 (2003). CAS  Google Scholar  * Liu, X. C., Zhang, H. W. & Lu, K. Formation of nanolaminated structure in an

interstitial-free steel. _Scr. Mater._ 95, 54–57 (2015). Article  ADS  CAS  Google Scholar  * Tabor, D. The Hardness of Metals, (Clarendon Press, Oxford, 1951). * Ke, X. et al. Ideal maximum

strengths and defect-induced softening in nanocrystalline-nanotwinned metals. _Nat. Mater._ 18, 1207–1214 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Malow, T. R. & Koch, C. C.

Mechanical properties, ductility, and grain size of nanocrystalline iron produced by mechanical attrition. _Metall. Mater. Trans. A_ 29A, 2285–2295 (1998). Article  ADS  CAS  Google Scholar

  * Wu, X., Jiang, P., Chen, L., Yuan, F. & Zhu, Y. T. Extraordinary strain hardening by gradient structure. _Proc. Natl Acad. Sci. USA_ 111, 7197–7201 (2014). Article  ADS  CAS  PubMed

  PubMed Central  Google Scholar  * Astafurova, E. G., Zakharova, G. G., Naydenkin, E. V., Raab, G. I. & Dobatkin, S. V. Structure and mechanical properties of low-carbon

ferrite-pearlite steel after severe plastic deformation and subsequent high-temperature annealing. _Phys. Mesomech._ 14, 195–203 (2011). Article  Google Scholar  * Jang, D. & Atzmon, M.

Grain-boundary relaxation and its effect on plasticity in nanocrystalline Fe. _J. Appl. Phys._ 99, 083504 (2006). Article  ADS  Google Scholar  * Detor, A. J. & Schuh, C. A.

Microstructural evolution during the heat treatment of nanocrystalline alloys. _J. Mater. Res._ 22, 3233–3248 (2007). Article  ADS  CAS  Google Scholar  * Porter, D. A. & Easterling, K.

E. Phase Transformations in Metals and Alloys, (Van Nostrand Reinhold, 1992). * Kaufman, L. & Cohen, M. Thermodynamics and kinetics of martensitic transformations. _Prog. Metal. Phys._

7, 165–246 (1958). Article  ADS  CAS  Google Scholar  * Sutton, A. P. & Balluffi, R. W. Interfaces in Crystalline Materials (1995). * James, D. W. & Leak, G. M. Grain boundary

diffusion of iron, cobalt and nickel in alpha-iron and of iron in gamma-iron. _Philos. Mag._ 12, 491–503 (1965). Article  ADS  CAS  Google Scholar  * Divinski, S. V., Hisker, F., Kang,

Y.-S., Lee, J.-S. & Herzig, C. Tracer diffusion of 63Ni in nano-γ-FeNi Produced by powder metallurgical method: systematic investigations in the C, B, and A diffusion regimes. _Interface

Sci._ 11, 67–80 (2003). Article  CAS  Google Scholar  * Divinski, S., Rösner, H. & Wilde, G. Functional nanostructured materials-microstructure, thermodynamic stability and atomic

mobility. _Front. Nanosci._ 1, 1–50 (2009). Article  Google Scholar  * Rösner, H., Koch, C. T. & Wilde, G. Strain mapping along Al–Pb interfaces. _Acta Mater._ 58, 162–172 (2010).

Article  ADS  Google Scholar  * Rösner, H. et al. Strain mapping of a triple junction in nanocrystalline Pd. _Acta Mater._ 59, 7380–7387 (2011). Article  ADS  Google Scholar  * Ungár, T.

& Borbély, A. The effect of dislocation contrast on x-ray line broadening: a new approach to line profile analysis. _Appl. Phys. Lett._ 69, 3173–3175 (1996). Article  ADS  Google Scholar

  * Ovid’ko, I. A., Valiev, R. Z. & Zhu, Y. T. Review on superior strength and enhanced ductility of metallic nanomaterials. _Prog. Mater. Sci._ 94, 462–549 (2018). Article  Google

Scholar  * Kumar, K. S., Van Swygenhoven, H. & Suresh, S. Mechanical behavior of nanocrystalline metals and alloys. _Acta Mater._ 51, 5743–5774 (2003). Article  ADS  CAS  Google Scholar

  * Yamakov, V., Wolf, D., Phillpot, S. R., Mukherjee, A. K. & Gleiter, H. Dislocation processes in the deformation of nanocrystalline aluminium by molecular-dynamics simulation. _Nat.

Mater._ 1, 45–49 (2002). Article  ADS  CAS  PubMed  Google Scholar  * Van Swygenhoven, H. Polycrystalline materials. Grain boundaries and dislocations. _Science_ 296, 66–67 (2002). Article 

PubMed  Google Scholar  * Zhang, Z. et al. Dislocations in grain boundary regions: the origin of heterogeneous microstrains in nanocrystalline materials. _Metall. Mater. Trans. A_ 51,

513–530 (2019). Article  Google Scholar  * Budrovic, Z., Swygenhoven, H. V., Derlet, P. M., Petegem, S. V. & Schmitt, B. Plastic deformation with reversible peak broadening in

nanocrystalline nickel. _Science_ 304, 273–276 (2004). Article  ADS  CAS  PubMed  Google Scholar  * Wang, Y. B. et al. Dislocation density evolution during high pressure torsion of a

nanocrystalline Ni-Fe alloy. _Appl. Phys. Lett._ 94, 091911 (2009). Article  ADS  Google Scholar  * Zhao, Y. H., Liao, X. Z., Jin, Z., Valiev, R. Z. & Zhu, Y. T. Microstructures and

mechanical properties of ultrafine grained 7075 Al alloy processed by ECAP and their evolutions during annealing. _Acta Mater._ 52, 4589–4599 (2004). Article  ADS  CAS  Google Scholar  *

Saada, G. From the single crystal to the nanocrystal. _Philos. Mag._ 85, 3003–3018 (2005). Article  ADS  CAS  Google Scholar  * Holzer, J. C., Birringer, R., Eckert, J., krill, C. E. III

& Johnson, W. L. Relaxation and grain growth behavior of nanocrystalline iron. _MRS Online Proc. Libr._ 272, 283–288 (1992). Article  CAS  Google Scholar  * Leslie, W. C. Iron and its

dilute substitutional solid solutions. _Metall. Mater. Trans. B_ 3, 5–26 (1972). Article  ADS  CAS  Google Scholar  * Kelly, A. Strong Solids, (Clarendon Press 1973). * Zhu, T. & Li, J.

Ultra-strength materials. _Prog. Mater. Sci._ 55, 710–757 (2010). Article  Google Scholar  * Hasnaoui, A., Swygenhoven, H. V. & Derlet, P. M. On non-equilibrium grain boundaries and

their effect on thermal and mechanical behaviour: a molecular dynamics computer simulation. _Acta Mater._ 50, 3927–3939 (2002). Article  ADS  CAS  Google Scholar  * Wilde, G. et al.

Plasticity and grain boundary diffusion at small grain sizes. _Adv. Eng. Mater._ 12, 758–764 (2010). Article  Google Scholar  * Ovid’ko, I. A., Sheinerman, A. G. & Valiev, R. Z.

Dislocation emission from deformation-distorted grain boundaries in ultrafine-grained materials. _Scr. Mater._ 76, 45–48 (2014). Article  Google Scholar  * Standard test methods for

determining average grain size; E112. Annual Book of ASTM Standards. Philadelphia: American Society for Testing and Materials (2000). p. 245. * Katnagallu, S. et al. Nanoglass-nanocrystal

composite-a novel material class for enhanced strength-plasticity synergy. _Small_ 16, e2004400 (2020). Article  PubMed  Google Scholar  * Movaghar Garabagh, M. R., Hossein Nedjad, S. &

Nili Ahmadabadi, M. X-ray diffraction study on a nanostructured 18Ni maraging steel prepared by equal-channel angular pressing. _J. Mater. Sci._ 43, 6840–6847 (2008). Article  ADS  CAS 

Google Scholar  * Ungár, T., Ott, S., Sanders, P. G., Borbély, A. & Weertman, J. R. Dislocations, grain size and planar faults in nanostructured copper determined by high resolution

X-ray diffraction and a new procedure of peak profile analysis. _Acta Mater._ 46, 3693–3699 (1998). Article  ADS  Google Scholar  * Ungár, T., Gubicza, J., Ribárik, G. & Borbely, A.

Crystallite size distribution and dislocation structure determined by diffraction profile analysis principles and practical application to cubic and hexagonal crystals. _J. Appl.

Crystallogr._ 34, 298–310 (2001). Article  Google Scholar  * Ungár, T., Dragomir, I., Révész, Á. & Borbély, A. The contrast factors of dislocations in cubic crystals: the dislocation

model of strain anisotropy in practice. _J. Appl. Crystallogr._ 32, 992–1002 (1999). Article  Google Scholar  Download references ACKNOWLEDGEMENTS The authors thank Prof. K. Lu for his

insightful and constructive comments on this paper. We thank Dr. J. J. Wang and Dr. M. Y. Yan for the help with sample preparation, Dr. S. N. Liu and H. Q. Ying for the synchrotron XRD test

and analysis, Dr. S. Fu for the help with Rietveld refinement. Q.Q.L. acknowledges National Natural Science Foundation of China under grant number 52001166. T.F. acknowledges support from

National Natural Science Foundation of China under grant numbers 51520105001 and 51571119, Fundamental Research Funds for the Central Universities under grant number 30919011404, Qing Lan

project of Jiangsu province and Distinguished professor project of Jiangsu province. Z.D.K. acknowledges Natural Science Foundation of Jiangsu Province under grant number BK20210352. S.L.

acknowledges National Natural Science Foundation of China under grant number 51871120, the National Key R&D Program of China (No. 2021YFB3802800), Natural Science Foundation of Jiangsu

Province under grant number BK20200019. This research used the resources of the Advanced Photon Source, a US Department of Energy (DOE) Office of Science User Facility operated for the DOE

Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357, and was supported by the US DOE Office of Science, Office of Basic Energy Sciences. AUTHOR INFORMATION

Author notes * Qingquan Lai Present address: Key laboratory for Light-Weight Materials, Nanjing Tech University, Nanjing, 211816, China * These authors contributed equally: Shangshu Wu,

Zongde Kou. AUTHORS AND AFFILIATIONS * Herbert Gleiter Institute of Nanoscience, School of Material Science and Engineering, Nanjing University of Science and Technology, Nanjing, 210094,

China Shangshu Wu, Zongde Kou, Qingquan Lai, Si Lan, Horst Hahn, Gerhard Wilde, Herbert Gleiter & Tao Feng * Institute of Nanotechnology, Karlsruhe Institute of Technology, Karlsruhe,

76021, Germany Shyam Swaroop Katnagallu & Horst Hahn * Institute of Materials Physics, University of Münster, Münster, 48149, Germany Shabnam Taheriniya, Gerhard Wilde & Herbert

Gleiter * Shenyang National Laboratory for Materials Science, Institute of Metal Research, Chinese Academy of Sciences, Shenyang, 110016, China Herbert Gleiter Authors * Shangshu Wu View

author publications You can also search for this author inPubMed Google Scholar * Zongde Kou View author publications You can also search for this author inPubMed Google Scholar * Qingquan

Lai View author publications You can also search for this author inPubMed Google Scholar * Si Lan View author publications You can also search for this author inPubMed Google Scholar * Shyam

Swaroop Katnagallu View author publications You can also search for this author inPubMed Google Scholar * Horst Hahn View author publications You can also search for this author inPubMed 

Google Scholar * Shabnam Taheriniya View author publications You can also search for this author inPubMed Google Scholar * Gerhard Wilde View author publications You can also search for this

author inPubMed Google Scholar * Herbert Gleiter View author publications You can also search for this author inPubMed Google Scholar * Tao Feng View author publications You can also search

for this author inPubMed Google Scholar CONTRIBUTIONS T.F. and Q.Q.L. designed the research. S.S.W. and Z.D.K. prepared and characterized the samples. Z.D.K., S.L., S.S.K., and S.T.

conducted the TEM, synchrotron XRD, 3D-APT, and TEM-EDX analyses, respectively. S.S.W., Z.D.K., Q.Q.L., H.H., G.W., T.F., and H.G. analyzed the data and discussed the results. S.S.W.,

Q.Q.L., H.H., G.W., T.F., and H.G. wrote the manuscript. All authors reviewed and contributed to the final manuscript. CORRESPONDING AUTHORS Correspondence to Qingquan Lai or Tao Feng.

ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature Communications_ thanks Xavier Sauvage and the other,

anonymous, reviewers for their contribution to the peer review of this work. Peer reviewer reports are available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with

regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION PEER REVIEW FILE RIGHTS AND PERMISSIONS OPEN ACCESS

This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as

long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third

party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the

article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright

holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Wu, S., Kou, Z., Lai, Q. _et al._

Dislocation exhaustion and ultra-hardening of nanograined metals by phase transformation at grain boundaries. _Nat Commun_ 13, 5468 (2022). https://doi.org/10.1038/s41467-022-33257-1

Download citation * Received: 20 January 2022 * Accepted: 08 September 2022 * Published: 17 September 2022 * DOI: https://doi.org/10.1038/s41467-022-33257-1 SHARE THIS ARTICLE Anyone you

share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the

Springer Nature SharedIt content-sharing initiative