Increasing the hilbert space dimension using a single coupled molecular spin

ABSTRACT Quantum technologies are expected to introduce revolutionary changes in information processing in the near future. Nowadays, one of the main challenges is to be able to handle a

large number of quantum bits (qubits), while preserving their quantum properties. Beyond the usual two-level encoding capacity of qubits, multi-level quantum systems are a promising way to

extend and increase the amount of information that can be stored in the same number of quantum objects. Recent work (Kues et al. 2017), has shown the possibility to use devices based on

photonic integrated circuits to entangle two qudits (with “d” being the number of available states). In the race to develop a mature quantum technology with real-world applications, many

possible platforms are being investigated, including those that use photons, trapped ions, superconducting and silicon circuits and molecular magnets. In this work, we present the electronic

read-out of a coupled molecular multi-level quantum systems, carried by a single Tb2Pc3 molecular magnet. Owning two magnetic centres, this molecular magnet architecture permits a 16

dimensions Hilbert space, opening the possibility of performing more complex quantum algorithms. SIMILAR CONTENT BEING VIEWED BY OTHERS QUANTUM TOMOGRAPHY OF AN ENTANGLED THREE-QUBIT STATE

IN SILICON Article 07 June 2021 A MANY-BODY QUANTUM REGISTER FOR A SPIN QUBIT Article Open access 24 January 2025 EXPERIMENTAL REALISATION OF MULTI-QUBIT GATES USING ELECTRON PARAMAGNETIC

RESONANCE Article Open access 02 November 2023 INTRODUCTION For some decades, significant efforts have been invested in quantum information research, with the promise to revolutionise the

way information is stored and processed. The strength of quantum computing lies in the possibility of using a coherent superposition of states, and interference between them, which enables a

class of algorithms that are not accessible to classical computers. To achieve this goal, it is first mandatory to coherently manipulate and read-out a two-state system (qubit), as

demonstrated in photonic devices1, trapped ions2,3, superconducting circuits4, electronic spins in two-dimensional electron gases (2DEG)5,6, phosphorous atom impurities in silicon7,8,9,10,

nitrogen-vacancy (NV) centres11,12, or molecular systems13,14, among others. The second step consists of the interconnection of _N_ entangled qubits, spanning the number of states to 2_N_,

while preserving their quantum properties, in order to allow information processing, as demonstrated for example in superconducting circuits15,16,17, two-dimensional electron gases5,6,

silicon devices18 and magnetic molecules19,20. Towards the aim of scalability, the number of interconnected qubits has to be increased, as demonstrated by the 16-qubit processor of the IBM

Q-experience21, a 72-qubit quantum chip announced by Google22, a 19-qubits computer tested by Rigetti23, and a silicon spin-based 2-qubits processor obtained by QuTech24. More recently, even

a NASA-Google partnership has claimed quantum supremacy25. Among these results, qudits, have been proposed as an alternative path towards the enlargement of the number of available quantum

states for computation26,27,28,29, as qudits allow to increase the number of states for the same number of quantum systems. Recently, the coupling of qudits has even been obtained using

photons30. In their work, Kues et al. demonstrated an approach in which photons, possessing multiple high-purity frequency modes, are generated on an integrated micro-chip. With _d_ = 10,

they confirmed a 100-dimension Hilbert space, and validated this platform by measuring Bell inequality violations and performing quantum state tomography. Towards this alternative, magnetic

molecules possessing magnetic memory, better known as Single Molecule Magnets (SMMs), are a promising spin qudits platform13,14,31. These systems have the advantage of being synthesised in

thousands of identical units and can be integrated in devices through bottom-up approaches, retaining their intrinsic magnetic properties32,33,34. SMMs can also be tailored through the use

of different metal ions and ligands compositions for their integration in devices. Likewise, SMMs have been shown to exhibit quantum phenomenon such as Quantum Tunnelling of the

Magnetisation (QTM)35,36,37,38, quantum phase interference39,40, and coherent spin manipulation with coherence times of the order of 1 μs41. This is the case of a

_bis_(phthalocyaninato)terbium(III) SMM (TbPc2), which has been integrated into transistor-like configurations42,43,44,45 as well as in carbon-nanotube transistors46,47. Different studies

have shown its magnetic resilience when deposited on surfaces, and the Tb3+ ion redox stability34. In the TbPc2, the π-electron system on the ligand eases the electric conduction, enabling

electric read-out42,44 of the nuclear spin _I_ = 3/2 carried by the Tb3+ ion. With coherence time of the order of 300 μs, the coherent manipulation of the different nuclear spin states was

demonstrated, leading to the implementation of the Grover algorithm using this nuclear spin qudit45. This strategy clearly highlights the potential of qudits, as long coherence times and

quantum algorithms have been achieved without requiring inter-qubit coupling. In this context, increasing the Hilbert space dimension is an appealing option for implementing more complex

quantum algorithms or universal reversible quantum logic gates, such as the Fredkin or Toffoli gates. Herein, in the quest of molecular spin systems with larger accessible Hilbert space, we

present the first electrical read-out of the nuclear spin states, carried by a coupled multi-level system, achieved with a single-molecular unit of Tb3+ triple-decker phthalocyanine,

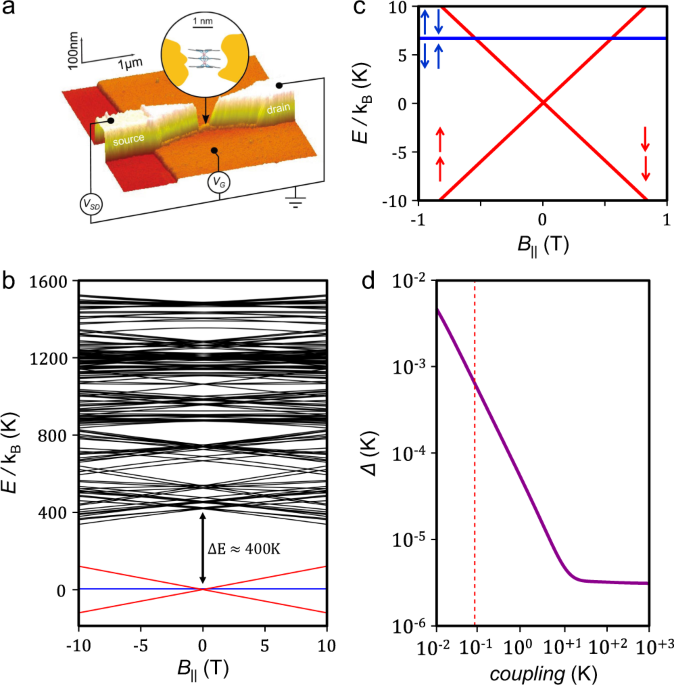
incorporated in a three-terminal transistor (Fig. 1a). We show that the magnetic moment of the two Tb3+ ions effectively couples with the electronic structure of the Pc ligands allowing the

electronic read-out of the nuclear spin states. More importantly, we observe the indirect coupling between the nuclear spin states residing on the Tb3+ ions. We emphasise here that there is

no entanglement between the two electronics or nuclear spins, but a larger Hilbert space dimension (_d_ = 16) can be achieved via indirect interaction between the nuclear spins. Indeed,

these results could represent an alternative for the realisation of more complex quantum algorithms using a single-molecular multi-level system. RESULTS TB2PC3 SINGLE-MOLECULE MAGNET to

probe our coupling scheme, we chose a tris(phthalocyaninato)di(terbium(III)) Tb2Pc3 SMM, composed of two Tb3+ ions and three phthalocyaninato (Pc) ligands. Both terbium ions sit on a

distorted square antiprism geometry. As the TbPc2 analogue, the total angular momentum _J_ = _L_ + _S =_ 6 characterises the [Xe]4_f_8 electronic shell of each Tb3+ metal ion. Note that the

strong spin-orbit coupling separates the _J_ = 6 state from the _J_ = 5 by 2900 K, hence, at common operating temperatures, solely the _J_ = 6 is considered. At a molecular level, the ligand

field in which the Tb3+ is located, created by the Pc ligands, leads to a doublet electronic ground state with strong uniaxial anisotropy. To calculate the Zeeman diagram for the Tb2Pc3

molecule, a ligand field Hamiltonian for _C_4 geometry is expressed in the Stevens operators formalism: $${H}_{{lf}}^{i}={{\langle }}{r}^{2}{{\rangle

}}{u}_{2}{A}_{2}^{0}{O}_{2}^{0}+{{\langle }}{r}^{4}{{\rangle }}{u}_{4}({A}_{4}^{0}{O}_{4}^{0}+{A}_{4}^{4}{O}_{4}^{4})+{{\langle }}{r}^{6}{{\rangle

}}{u}_{6}({A}_{6}^{0}{O}_{6}^{0}+{A}_{6}^{4}{O}_{6}^{4})$$ (1) and the Zeeman Hamiltonian, $${H}_{{{{{\mathrm{Zeeman}}}}}}^{i}={g}_{J}{\mu }_{0}{\mu }_{B}{J}_{{||}}^{i}\cdot

{B}_{{{{\rm{||}}}}}\,$$ (2) where in (1) _u__i_ are the Stevens factors, \({O}_{i}^{j}\,\) are the Stevens operator and \({A}_{i}^{j}\) <_r__j_> are the ligand field parameters. In (2)

_g__J_, _J_ and \({{{{\boldsymbol{B}}}}}_{{{{\boldsymbol{||}}}}}\) are respectively the gyromagnetic ratio of Tb3+, the electronic moment operator of Tb3+ and the applied field vector. The

presence of \({O}_{i}^{j}\) provides a strong anisotropy to Tb2Pc3, causing an energy gap of ca. 400 K between the _m__J_ = \({|}\!{\pm} \!6\rangle\) and the _m__J_ =

\({|}\!{\pm}\!5\rangle\) electronic states. µ-SQUID48 and ab-initio CASSCF49 studies have revealed the anisotropy of the _m__J_ = \({|}\!{\pm}\!6\rangle\) doublet state of the Tb3+ ions to

have an easy axis perpendicular to the Pc planes. Moreover, both Tb3+ ions in the dimer are coupled through a ferromagnetic interaction, therefore, the Hamiltonian considering the ligand

field and the interaction is: $${H}_{{{{{{\mathrm{Tb}}}}}}_{2}}={H}_{{{{{\mathrm{lf}}}}}}^{i}+{H}_{{{{{\mathrm{Zeeman}}}}}}^{i}-C{J}_{1}{J}_{2}$$ (3) where the first accounts for the ligand

field for each Tb3+ ion, the second term is the Zeeman term and the third term represents the coupling between the electronic spin of the Tb3+ ions. Figure 1b shows the Zeeman diagram

corresponding to the diagonalization of the (2_J_ + 1)·(2_J_ + 1) matrix. At zero field, the ferromagnetic ground state \({|}\!{\pm}\!6,{\pm}\!6\rangle\) and the antiferromagnetic excited

state \({|}\!{\pm}\!6,\mp 6\rangle\) are separated from the first excited state \({|}\!{\pm}\! 5,{\pm}\!5\rangle\) by Δ_E_ ≈ 400 K (Fig. 1b). Note that at our experimental electronic

temperatures (≈80 mK) only the _m__J_ = \({|}\!{\pm}\! 6,{\pm}\! 6\rangle\) is populated. The presence of the transverse terms \({O}_{4}^{4}\) and \({O}_{6}^{4}\) in the ligand field

Hamiltonian induces mixing of the \({|}\!+\!6,+6\rangle\) and \({|}\!-\!6,-6\rangle\) states via \({J}_{4}^{\pm }\), resulting in an opening of the anti-crossing between the \({|}\!{\pm}\!

6,{\pm}\! 6\rangle\) states. At very low temperatures, this opening acts as a relaxation pathway for the temperature-independent relaxation of the magnetisation, i.e., QTM process. At the

anti-crossings the tunnelling probability is governed by the Landau–Zener equation: $${P}_{m,m^{\prime} }=1-{\exp }\left(-\frac{\pi {\Delta }_{m,m^{\prime} }^{2}}{2{{\hslash }}{g}_{J}{{{\mu

}}}_{{{{\mathrm{B}}}}}\left|m-m^{\prime} \right|{{{\mu }}}_{0}{{{\mathrm{d}}}}{H}_{\parallel }/{{{{\mathrm{d}}}}t}}\right)$$ (4) where µ0 is the vacuum permeability, _µ_B is the Bohr

magneton, _m_ and _m_′ are the two states involved (\(\left|m-m^{\prime} \right|\) = 24 for Tb2Pc3) and \({\Delta }_{m,m^{\prime} }^{2}\) is the anti-crossing splitting energy, which is

contingent upon the coupling between the _J_1 and _J_2 states. Calculation of \({\Delta }_{m,m^{\prime} }^{2}\) for different ferromagnetic coupling values _C_ is presented in Fig. 1d. The

red dashed line represents the crossing between the ferromagnetic and antiferromagnetic states48. From this value, we obtain \({\Delta }_{m,m^{\prime} }\) = 0.6 mK. This large value of the

anti-crossing energy results in a Landau–Zener probability _P__m,m_′ = 1 even for magnetic field sweeping rates of 103 T/s. As the maximum magnetic field sweeping rate accessible for the

experiment was lower than 100 mT/s, reversal of the magnetisation is only governed by QTM, and no direct relaxation from the ferromagnetic state to the antiferromagnetic one was observed. Up

to this point, solely the electronic states of Tb2Pc3 have been considered. From now on, we consider the nuclear spin _I_ = 3/2 carried by each Tb3+ ions. Considering the strong hyperfine

interaction, each \({|}\!{\pm}\!6\rangle\) ground state is split into four states unevenly separated corresponding to _m_I = ±3/2, ±1/2. The effect of the nuclear spins and quadrupolar

interaction is considered in the following Hamiltonian: $${H}_{{{{{\mathrm{hf}}}}}}^{i}={A}_{{{{{\mathrm{hf}}}}}}{I}^{i}{J}^{i}+P{({I}^{i})}^{2}$$ (5) where _A_ = 30.9 mK and _P_ = 14.4 mK

are the hyperfine interaction and the quadrupolar constants respectively, considered to be the same for both Tb3+ sites48. As nuclear spins have magnetic moments ~2000 times smaller than

electronic spins, direct nuclear spin interaction can be safely neglected. In contrast, the nuclear spins can be indirectly coupled via the dipolar interaction between the Tb3+ ions,

resulting in 4·4 = 16 possible nuclear spin states. Hamiltonian in Eq. (6) accounts for all interactions in Tb2Pc3.

$${H}_{{{{{{\mathrm{Tb}}}}}}_{2}}={H}_{{{{{\mathrm{lf}}}}}}^{i}+{H}_{{{{{\mathrm{Zeeman}}}}}}^{i}+{H}_{{{{{\mathrm{hf}}}}}}^{i}-C{J}_{1}{J}_{2}$$ (6) Numerical diagonalization of the

Hamiltonian in Eq. (6) results in a ferromagnetic ground state with multiple level-crossings in the range \({B}_{\parallel }\) = ±46 mT (Fig. 2a). The square regions in Fig. 2b indicate the

anti-crossings. In these regions, electronic spins reversal is allowed via QTM, while preserving the nuclear spin states. As calculated, a total of 10 anti-crossings allow the reversal of

the electronic spins. Nevertheless, at three of these positions the electronic spins reversal occurs at the same magnetic field \({B}_{\parallel }\), therefore, only seven positions in the

magnetic field where QTM occurs should be observed. MOLECULAR SPIN STATES READ-OUT the nuclear spin states read-out of the Tb2Pc3 molecular magnet was studied via transport measurements

through the molecule while sweeping the external magnetic field in two directions. The quantum dot is defined by the Pc ligands which are known to be good electrical conductors due to their

π delocalised links. Moreover, the overlap between the 4_f_ shell of the Tb3+ ions and the π delocalised links of the Pc ligands give rise to an exchange coupling44. Our detection scheme is

then based on an exchange interaction between the electronic spin of the Tb3+ ions and the nearby Pc read-out quantum dot. The coupling between the two systems results in a spin-dependent

conductance through the read-out dot and establishes an all-electrical single spin detection. Sweeping back and forth the external magnetic field _B__X_ in the direction of the coil, the

differential conductance is simultaneously recorded using a digital lock-in amplifier. Additionally, a constant external magnetic field _B__Y_ is applied along the other direction of the

coil. Considering a single magnetic field sweep, we observe an abrupt jump in the differential conductance as presented in Fig. 3a. This abrupt variation is due to the reversal of the

electronic spins carried by the two Tb3+ ions42,43,44,45,46,47,50. Sweeping _B__X_ back and forth, a hysteresis is clearly observed in Fig. 3a. By measuring the difference of the

differential conductance Δ(d_I_/d_V_) while sweeping back and forth the magnetic field _B__X_, for different values of _B__Y_, we observe different regions where abrupt jumps are measured

(Fig. 3a). From now on, we will focus on the magnetic field region highlighted by the green double arrow in Fig. 3b. Other regions correspond to other molecular systems for which the nuclear

spin signatures were not resolved. Figure 3c presents the histogram compiling the differential conductance jump positions for 6000 back and forth magnetic field _B__X_ sweeps at 50 mT/s

with an additional constant _B__Y_ = 1 T. Note that we were not able to sweep the external magnetic field in the direction of the easy axis of the Tb2Pc3 molecular system due to a missing

coil in the Z-direction of our experimental setup. As presented in Fig. 3c, two main features are observed: (i) peaks in the histogram with a high amplitude and roughly equally spaced, (ii)

peaks in the histogram with a smaller amplitude and width and unequally spaced from the previous ones. (i) We first focus on the main feature corresponding to the peaks in the histogram with

a high amplitude and relatively large width (counts framed in grey in Fig. 3c). Seven peaks are observed, corresponding to the ten anti-crossings where tunnelling is allowed as expected

from the theoretical predictions. Note here that the experimental values do not correspond to the QTM positions expected from Eq. (6); consequence of the miss-alignment of the easy axis of

the Tb2Pc3 molecule with our applied magnetic field. As a result, while the positions of the QTM in a parallel magnetic field are expected within \({B}_{\parallel }\) = ±46 mT, the measured

positions using an external magnetic field occur within _B__X_ = ±55 mT. (ii) Two additional peaks are clearly visible at magnetic field _B__X_ higher than +55 mT and lower than −55 mT.

First, the amplitude of these two peaks is lower compared to the amplitude of the main seven peaks. Moreover, the magnetic field spacing is lower than the spacing obtained for the main seven

peaks. Therefore, these additional peaks in the histogram could be attributed to signatures of another molecular system we were not able to distinguish. This phenomenon will need further

investigations and is a probable source of the large envelope observed in Fig. 3c, d. It is important to state that additional peaks should also be present in between those two, but the

amplitude is too low to be observable. However, in the following studies, quantitative measurements could be approximative, as an accurate determination of the different nuclear spin states

population would require not to take into account these additional peaks events, with a much lower amplitude, that could not be discriminated from the main seven peaks. We now present the

study of the probability of the QTM events considering the states degeneracy and the positions of the anti-crossings. For both coupled Tb3+ ions, a total of 16 states is expected. As

described earlier, out of these 16 states, 10 are not degenerate, while three of the anti-crossings occur at the same magnetic field. As a result, a total of seven states are truly

observable. The nuclear spins states distribution can be obtained considering the 16 states as follows: the two most external peaks at ±55 mT (positions #1 and #7) have a probability _P_ = 

1/16 each, while the two immediate neighbours at ± 38 mT (positions #2 and #6) and ±20 mT (positions #3 and #5) account for _P_ = 2/16 and _P_ = 3/16 respectively. Finally, the events at

zero magnetic field (position #4) have _P_ = 4/16, which corresponds to the double electronic spin reversal for 4 different nuclear spins. The results are summarised in Table 1. COUPLED

NUCLEAR SPINS DYNAMICS The dynamic of the nuclear spins was studied analysing the same 6000 back and forth magnetic field sweeps. A correlation cartography of the identified abrupt

conductance jump positions is presented in Fig. 4a. The abscissa corresponds to the reversal of the electronic spins during the field sweep, while the ordinate corresponds to a reversal

during the next sweep. The white dashed lines indicate the anti-crossing positions for which events are predicted. In order to ease the reading, a Gaussian filter is used to bring out the

density of the local events. The utility of this correlation cartography is twofold: (i) first we obtain a better visualisation of the nuclear spins states; (ii) we can visualise to what

extent the quantum system remains in the same nuclear spins state in between two sweeps through the anti-crossing regions. Using the correlation cartography, it is possible to obtain an

estimation of the lifetime of the nuclear spin states compared to the measurement time (≈3 s). As the two axes correspond to the trace and retrace _B__X_ magnetic field sweeps, two

subsequent measurements with the same nuclear spin states are situated on the diagonal of the correlation map, whereas the off-diagonal positions correspond to nuclear spin state relaxation

or excitation. As presented in Fig. 4, the correlation cartography does not exhibit an excess of events on the diagonal. It reveals a nuclear spins states lifetime shorter than the

measurement time. Moreover, taking into account that the seven anti-crossing regions have different degeneracies, we renormalized the event counts as per the cumulated degeneracy of the

corresponding abscissa and ordinate anti-crossings. The result is presented in the histogram Fig. 4b. We observe a higher population of the up left and bottom right blocks, clearly

demonstrating the quantum system relaxation in between two consecutive measurements. A more detailed insight into the effective temperature of the nuclear spins states has been obtained by

analysing the population of the states for 6000 forward magnetic field (sweeps from negative to positive magnetic field values). We present in Fig. 5a the renormalisation of the populations

of the different nuclear spins states as per each anti-crossing degeneracy. Due to a low lifetime compared to the measurement time, the occupancy of states exhibits a relaxation towards a

thermal equilibrium, as shown by the measurement of a higher population for the nuclear spin states with lower energies. To obtain a quantitative analysis of the temperature of the nuclear

spins, we used Maxwell–Boltzmann statistics: $$\frac{{N}_{i}}{N}=\frac{{g}_{i}{e}^{\frac{-{E}_{i}}{{k}_{{{{\mathrm{B}}}}}T}}}{Z(T)}\,{{{\rm{with}}}}\,Z(T)=\mathop{\sum

}\limits_{i=1}^{n}{e}^{\frac{-{E}_{i}}{{k}_{{{{\mathrm{B}}}}}T}}$$ where _Z_(_T_) is the system partition function, _k_B is the Boltzmann constant, _T_ is the temperature, _E__i_ are the

energies separation compared to the lowest energy level, and _g__i_ their respective degeneracies. _N__i_ is the population of each state, with the total population \(N=\mathop{\sum

}\nolimits_{i=1}^{n}{N}_{i}\). Note that _N__i_/_g__i_ is the normalisation used previously for the correlation cartography. From this study, we obtain an effective temperature _T_ ≈ 290 mK

of the nuclear spins, which is consistent with the one obtained on a TbPc2 molecular magnet, measured with a comparable experimental set-up. We believe that the short lifetimes could be a

result of flow current through the Tb2Pc3 unit, which induces a larger FWHM, and thus decreases the fidelity of the system50. Herein we have presented the electrical transport measurements

of a Tb2Pc3 molecule embedded in a transistor, resulting in the first electronic read-out of a single coupled molecular spin. The read-out procedure consists of the detection of abrupt

conductance jumps induced by the QTM of the electronic spins, in agreement with theoretical predictions. The seven measured QTM positions in magnetic fields are a direct consequence of the

indirect coupling of the nuclear states residing in each Tb3+ ion via the electronic interaction. Moreover, we estimated a low lifetime compared to our measurement time which has been

observed and ascribed to the current flowing through the molecular unit50. These two aspects can be certainly enhanced by device design. Our results clearly demonstrated the potential of

coupled multi-level systems to span the Hilbert space using a single-molecular magnet, an important characteristic for the realisation of more complex quantum algorithms. Furthermore, the

uneven separation of the different coupled nuclear spins would in principle allow the manipulation of each individual coupled state. These two characteristics may path the way to the

realisation of more complex algorithms such as Fredkin or Toffoli. METHODS NANOFABRICATION Gold nano-constrictions acting as source and drain electrodes are fabricated through e-beam angles

depositions, on the top of a gate composed of a metallic gold part and a high-k hafnium dioxide. It has to be noticed that the obtained electrodes arrow-like geometry enables to reduce the

screening effect of the gate electric field51. The molecules were diluted in a solvent and later deposited at room temperature after a chemical cleaning (reactive-ion etching) of the sample

surface. Afterwards, the electromigration process was achieved at low temperatures (4 K). The electromigration process consists of applying a difference of potential in between two

electrodes forming a nano-constriction, so that the conduction electrons put in motion the gold ions, until a nano-interstice is opened52. In order to control the interstice size, the

potential difference has to be precisely controlled with a real-time electronic. Thereby, when the conductance is below the so-called quantum of conductance (_G_0 = 2e2/_h_), the process is

stopped in around 10 μs. CRYOGENIC MEASUREMENT If the first conduction measurements between the source and drain electrodes were showing nano-metre size quantum dot signatures, the

magnetisation reversal measurements were performed in a 3He/4He dilution refrigerator so the sample temperature was below 100 mK. The cryostat used for this work was equipped with two coils,

generating up to 5.5 and 1.25 T with a maximum sweep rate up to 100 mT/s, and allows the sample to rotate with respect to them, providing a 3D control of the applied magnetisation. A more

detailed description of the sample fabrication and experimental set-up can be found in Chaps. 4 and 5 in ref. 53. DATA AVAILABILITY The data that supports the findings of this study are

available from the corresponding authors upon request. REFERENCES * Wang, J., Sciarrino, F., Laing, A. & Thompson, M. G. Integrated photonic quantum technologies. _Nat. Photonics_ 14,

273–284 (2020). Article  ADS  CAS  Google Scholar  * Blatt, R. & Wineland, D. Entangled states of trapped atomic ions. _Nature_ 453, 1008–1015 (2008). Article  ADS  CAS  PubMed  Google

Scholar  * Lu, Y. et al. Global entangling gates on arbitrary ion qubits. _Nature_ 572, 363–367 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Nakamura, Y., Pashkin, Y. A. & Tsai,

J. S. Coherent control of macroscopic quantum states in a single-Cooper-pair box. _Nature_ 398, 786–788 (1999). Article  ADS  CAS  Google Scholar  * Koppens, F. H. L. et al. Driven coherent

oscillations of a single electron spin in a quantum dot. _Nature_ 442, 766–771 (2006). Article  ADS  CAS  PubMed  Google Scholar  * Shulman, M. D. et al. Demonstration of entanglement of

electrostatically coupled singlet-triplet qubits. _Science_ 336, 202–205 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Morello, A. Atoms and circuits unite in silicon. _Nat.

Nanotechnol._ 8, 233–234 (2013). Article  ADS  CAS  PubMed  Google Scholar  * Pla, J. J. et al. High-fidelity readout and control of a nuclear spin qubit in silicon. _Nature_ 496, 334–338

(2013). Article  ADS  CAS  PubMed  Google Scholar  * Morello, A. et al. Single-shot readout of an electron spin in silicon. _Nature_ 467, 687–691 (2010). Article  ADS  CAS  PubMed  Google

Scholar  * Pla, J. J. et al. A single-atom electron spin qubit in silicon. _Nature_ 489, 541–544 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Fuchs, G. D., Dobrovitski, V. V., Toyli,

D. M., Heremans, F. J. & Awschalom, D. D. Gigahertz dynamics of a strongly driven single quantum spin. _Science_ 326, 1520–1522 (2009). Article  ADS  CAS  PubMed  Google Scholar  *

Childress, L. et al. Coherent dynamics of coupled electron and nuclear spin qubits in diamond. _Science_ 314, 281–285 (2006). Article  ADS  CAS  PubMed  Google Scholar  * Atzori, M. &

Sessoli, R. The second quantum revolution: role and challenges of molecular chemistry. _J. Am. Chem. Soc._ 141, 11339–11352 (2019). Article  CAS  PubMed  Google Scholar  * Gaita-Ariño, A.,

Luis, F., Hill, S. & Coronado, E. Molecular spins for quantum computation. _Nat. Chem._ 11, 301–309 (2019). Article  PubMed  CAS  Google Scholar  * DiCarlo, L. et al. Preparation and

measurement of three-qubit entanglement in a superconducting circuit. _Nature_ 467, 574–578 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Neeley, M. et al. Generation of three-qubit

entangled states using superconducting phase qubits. _Nature_ 467, 570–573 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Song, C. et al. 10-Qubit entanglement and parallel logic

operations with a superconducting circuit. _Phys. Rev. Lett._ 119, 180511 (2017). Article  ADS  PubMed  Google Scholar  * Veldhorst, M. et al. A two-qubit logic gate in silicon. _Nature_

526, 410–414 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Ferrando-Soria, J. et al. A modular design of molecular qubits to implement universal quantum gates. _Nat. Commun._ 7, 11377

(2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Atzori, M. et al. A two-qubit molecular architecture for electron-mediated nuclear quantum simulation. _Chem. Sci._ 9,

6183–6192 (2018). Article  CAS  PubMed  PubMed Central  Google Scholar  * García-Pérez, G., Rossi, M. A. C. & Maniscalco, S. IBM Q Experience as a versatile experimental testbed for

simulating open quantum systems. _npj Quantum Inf._ 6, 1 (2020). Article  ADS  Google Scholar  * Kelly, J. et al. State preservation by repetitive error detection in a superconducting

quantum circuit. _Nature_ 519, 66–69 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Otterbach, J. S. et al. Unsupervised machine learning on a hybrid quantum computer. Preprint at

https://arxiv.org/abs/1712.05771 (2017). * Watson, T. F. et al. A programmable two-qubit quantum processor in silicon. _Nature_ 555, 633–637 (2018). Article  ADS  CAS  PubMed  Google Scholar

  * Arute, F. et al. Quantum supremacy using a programmable superconducting processor. _Nature_ 574, 505–510 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Leuenberger, M. N. &

Loss, D. Quantum computing in molecular magnets. _Nature_ 410, 789–793 (2001). Article  ADS  CAS  PubMed  Google Scholar  * O’Leary, D. P., Brennen, G. K. & Bullock, S. S. Parallelism

for quantum computation with qudits. _Phys. Rev. A Mol. Opt. Phys._ 74, 032334 (2006). Article  ADS  CAS  Google Scholar  * Mohammadi, M., Niknafs, A. & Eshghi, M. Controlled gates for

multi-level quantum computation. _Quantum Inf. Process._ 10, 241–256 (2011). Article  MathSciNet  MATH  Google Scholar  * Hussain, R. et al. Coherent manipulation of a molecular ln-based

nuclear qudit coupled to an electron qubit. _J. Am. Chem. Soc._ 140, 9814–9818 (2018). Article  CAS  PubMed  Google Scholar  * Kues, M. et al. On-chip generation of high-dimensional

entangled quantum states and their coherent control. _Nature_ 546, 622–626 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Moreno-Pineda, E., Godfrin, C., Balestro, F., Wernsdorfer, W.

& Ruben, M. Molecular spin qudits for quantum algorithms. _Chem. Soc. Rev._ 47, 501–513 (2018). Article  CAS  PubMed  Google Scholar  * Mannini, M. et al. Quantum tunnelling of the

magnetization in a monolayer of oriented single-molecule magnets. _Nature_ 468, 417–421 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Mannini, M. et al. Magnetic memory of a

single-molecule quantum magnet wired to a gold surface. _Nat. Mater._ 8, 194–197 (2009). Article  ADS  CAS  PubMed  Google Scholar  * Moreno Pineda, E., Komeda, T., Katoh, K., Yamashita, M.

& Ruben, M. Surface confinement of TbPc2-SMMs: structural, electronic and magnetic properties. _Dalton Trans._ 45, 18417–18433 (2016). Article  CAS  PubMed  Google Scholar  * Friedman,

J. R., Sarachik, M. P., Tejada, J. & Ziolo, R. Macroscopic measurement of resonant magnetization tunneling in high-spin molecules. _Phys. Rev. Lett._ 76, 3830–3833 (1996). Article  ADS 

CAS  PubMed  Google Scholar  * Ishikawa, N., Sugita, M. & Wernsdorfer, W. Quantum tunneling of magnetization in lanthanide single-molecule magnets: Bis(phthalocyaninato)terbium and

bis(phthalocyaninato)dysprosium anions. _Angew. Chem. Int. Ed._ 44, 2931–2935 (2005). Article  CAS  Google Scholar  * Thomas, L. et al. Macroscopic quantum tunnelling of magnetization in a

single crystal of nanomagnets. _Nature_ 383, 145–147 (1996). Article  ADS  CAS  Google Scholar  * Sangregorio, C., Ohm, T., Paulsen, C., Sessoli, R. & Gatteschi, D. Quantum tunneling of

the magnetization in an iron cluster nanomagnet. _Phys. Rev. Lett._ 78, 4645–4648 (1997). Article  ADS  CAS  Google Scholar  * Wernsdorfer, W. & Sessoli, R. Quantum phase interference

and parity effects in magnetic molecular clusters. _Science_ 284, 133–135 (1999). Article  ADS  CAS  PubMed  Google Scholar  * Wernsdorfer, W., Soler, M., Christou, G. & Hendrickson, D.

N. Quantum phase interference (Berry phase) in single-molecule magnets of [Mn12]2-. _J. Appl. Phys._ 91, 7164–7166 (2002). Article  ADS  CAS  Google Scholar  * Bertaina, S. et al. Quantum

oscillations in a molecular magnet. _Nature_ 453, 203–206 (2008). Article  ADS  CAS  PubMed  Google Scholar  * Vincent, R., Klyatskaya, S., Ruben, M., Wernsdorfer, W. & Balestro, F.

Electronic read-out of a single nuclear spin using a molecular spin transistor. _Nature_ 488, 357–360 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Thiele, S. et al. Electrically

driven nuclear spin resonance in single-molecule magnets. _Science_ 344, 1135–1138 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Godfrin, C. et al. Electrical read-out of a single

spin using an exchange-coupled quantum dot. _ACS Nano_ 11, 3984–3989 (2017). Article  CAS  PubMed  Google Scholar  * Godfrin, C. et al. Operating quantum states in single magnetic molecules:

implementation of Grover’s quantum algorithm. _Phys. Rev. Lett._ 119, 187702 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Ganzhorn, M., Klyatskaya, S., Ruben, M. & Wernsdorfer,

W. Quantum Einstein-de Haas effect. _Nat. Commun._ 7, 11443 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Ganzhorn, M., Klyatskaya, S., Ruben, M. & Wernsdorfer, W.

Strong spin-phonon coupling between a single-molecule magnet and a carbon nanotube nanoelectromechanical system. _Nat. Nanotechnol._ 8, 165–169 (2013). Article  ADS  CAS  PubMed  Google

Scholar  * Moreno-Pineda, E. et al. Observation of cooperative electronic quantum tunneling: increasing accessible nuclear states in a molecular qudit. _Inorg. Chem._ 57, 9873–9879 (2018).

Article  CAS  PubMed  Google Scholar  * Horii, Y. et al. Highly oxidized states of phthalocyaninato terbium(III) multiple-decker complexes showing structural deformations, biradical

properties and decreases in magnetic anisotropy. _Chem. A Eur. J._ 26, 8621–8630 (2020). Article  CAS  Google Scholar  * Urdampilleta, M., Klyatskaya, S., Ruben, M. & Wernsdorfer, W.

Landau-Zener tunneling of a single Tb3+ magnetic moment allowing the electronic read-out of a nuclear spin. _Phys. Rev. B_ 87, 195412 (2013). Article  ADS  CAS  Google Scholar  * Datta, S.

S., Strachan, D. R. & Johnson, A. T. C. Gate coupling to nanoscale electronics. _Phys. Rev. B Condens. Matter Mater. Phys._ 79, 1–9 (2009). Article  CAS  Google Scholar  * Ho, P. S.

& Kwok, T. Electromigration in metals. _Rep. Prog. Phys._ 52, 301–348 (1989). Article  ADS  CAS  Google Scholar  * Biard, H. _Read-Out of a Nuclear Qubit Couple with a Molecular

Transistor_ (Université Grenoble Alpes, Grenoble, 2019). * Roch, N., Florens, S., Bouchiat, V., Wernsdorfer, W. & Balestro, F. Quantum phase transition in a single-molecule quantum dot.

_Nature_ 453, 633–637 (2008). Article  ADS  CAS  PubMed  Google Scholar  Download references ACKNOWLEDGEMENTS We thank E. Eyraud, C. Thirion, T. Crozes and L. Abbassi for help with cryogenic

set-up, maintenance, data collection and treatment, and sample preparation. We also thank S. Lumetti, M. Nale, M. Urdampilleta and J. Viennot for helpful discussions. H. B. kindly thanks

the 2015 AGIR-POLE-PEM programme for PhD funding. We acknowledge the DFG-TR 88 “3Met” (project A8) and the Karlsruhe Nano Micro Facility (KNMF, www.kit.edu/knmf) for the provision of access

to instruments at their laboratories. EMP thanks the Panamanian National System of Investigators (SNI, SENACYT) for support. W.W. thanks the A. v. Humboldt foundation and the ERC grant

MoQuOS No. 741276. FUNDING Open Access funding enabled and organized by Projekt DEAL. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * CNRS, Grenoble INP, Institut Néel, Univ. Grenoble Alpes,

Grenoble, France Hugo Biard, Edgar Bonet, Wolfgang Wernsdorfer & Franck Balestro * Depto. de Química-Física, Escuela de Química, Facultad de Ciencias Naturales, Exactas y Tecnología,

Universidad de Panamá, Panamá, Panamá Eufemio Moreno-Pineda * Institute of Nanotechnology (INT), Karlsruhe Institute of Technology (KIT), Eggenstein-Leopoldshafen, Germany Mario Ruben *

Centre Européen de Sciences Quantiques (CESQ) within the Institut de Science et d’Ingénierie Supramoléculaires (ISIS), Strasbourg Cedex, France Mario Ruben * Institute for Quantum Materials

and Technology (IQMT), Karlsruhe Institute of Technology (KIT), Eggenstein-Leopoldshafen, Germany Mario Ruben & Wolfgang Wernsdorfer * Physikalisches Institut, Karlsruhe Institute of

Technology, Karlsruhe, Germany Wolfgang Wernsdorfer Authors * Hugo Biard View author publications You can also search for this author inPubMed Google Scholar * Eufemio Moreno-Pineda View

author publications You can also search for this author inPubMed Google Scholar * Mario Ruben View author publications You can also search for this author inPubMed Google Scholar * Edgar

Bonet View author publications You can also search for this author inPubMed Google Scholar * Wolfgang Wernsdorfer View author publications You can also search for this author inPubMed Google

Scholar * Franck Balestro View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS H.B. prepared all samples, conducted the measurements and

analysed the data. F.B., M.R. and W.W. conceived the idea and supervised the project. The data were discussed and analysed by H.B., E.B., F.B. and W.W. E.B. created the software to conduct

the measurements in the device. The synthesis and bulk characterisation of the Tb2Pc3 molecule was conducted by E.M.-P. and M.R. The manuscript was written by H.B., E.M.-P. and F.B. and

discussed and analysed by all authors. CORRESPONDING AUTHORS Correspondence to Wolfgang Wernsdorfer or Franck Balestro. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no

competing interests. ADDITIONAL INFORMATION PEER REVIEW INFORMATION _Nature Communications_ thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer

reviewer reports are available. PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY

INFORMATION SUPPLEMENTARY INFORMATION PEER REVIEW FILE RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which

permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to

the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless

indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or

exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints

and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Biard, H., Moreno-Pineda, E., Ruben, M. _et al._ Increasing the Hilbert space dimension using a single coupled molecular spin. _Nat

Commun_ 12, 4443 (2021). https://doi.org/10.1038/s41467-021-24693-6 Download citation * Received: 04 September 2020 * Accepted: 30 April 2021 * Published: 21 July 2021 * DOI:

https://doi.org/10.1038/s41467-021-24693-6 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative