Laboratory measurements of the physics of auroral electron acceleration by alfvén waves

ABSTRACT While the aurora has attracted attention for millennia, important questions remain unanswered. Foremost is how auroral electrons are accelerated before colliding with the ionosphere

and producing auroral light. Powerful Alfvén waves are often found traveling Earthward above auroras with sufficient energy to generate auroras, but there has been no direct measurement of

the processes by which Alfvén waves transfer their energy to auroral electrons. Here, we show laboratory measurements of the resonant transfer of energy from Alfvén waves to electrons under

conditions relevant to the auroral zone. Experiments are performed by launching Alfvén waves and simultaneously recording the electron velocity distribution. Numerical simulations and

analytical theory support that the measured energy transfer process produces accelerated electrons capable of reaching auroral energies. The experiments, theory, and simulations demonstrate

a clear causal relationship between Alfvén waves and accelerated electrons that directly cause auroras. SIMILAR CONTENT BEING VIEWED BY OTHERS ALFVÉN WAVES IN THE SOLAR CORONA: RESONANCE

VELOCITY, DAMPING LENGTH, AND CHARGED PARTICLES ACCELERATION BY KINETIC ALFVÉN WAVES Article Open access 14 November 2024 PARTICLE-SOUNDING OF THE SPATIAL STRUCTURE OF KINETIC ALFVÉN WAVES

Article Open access 12 April 2023 VERY-LOW-FREQUENCY TRANSMITTERS BIFURCATE ENERGETIC ELECTRON BELT IN NEAR-EARTH SPACE Article Open access 24 September 2020 INTRODUCTION Space weather

embodies the study of how variable forcing by the Sun, mediated by the supersonically flowing solar wind, affects the near-Earth space environment1. One of the most spectacular displays of

the Sun’s effect on the Earth is the aurora, statistically appearing in an oval-shaped region around the magnetic poles at high latitude2, with manifestations on both the nightside and the

dayside. High-energy particles precipitating down along the Earth’s dipolar magnetic field into the auroral ionopshere collisionally excite atoms and molecules3, leading to the auroral

emissions with a variety of appearances, from bright discrete arcs, to faint arcs, to diffuse aurora. The differing magnetic local time and morphology of observed auroral events suggests

distinct source regions as well as differing mechanisms of generation, with a clear disconnect between dayside and nightside aurora4. Three main magnetospheric drivers for the aurora have

been identified5: (i) the precipitation of very energetic magnetosheath particles from the magnetospheric boundary layer on the dayside6 or plasma sheet electrons on the nightside7,8; (ii)

quasi-static, field-aligned currents9,10; or (iii) energetic electrons accelerated by Alfvénic fluctuations, either as field-line resonances (effectively global-scale standing Alfvén waves

in the Earth’s dipolar magnetic field)11 or Alfvén waves propagating down the field lines towards the auroral ionosphere12,13. For all of these cases, the detailed kinetic plasma physics

governing the flow of energy from the outer magnetosphere into precipitating energetic particles remains a topic of ongoing study. To confirm the acceleration of electrons by downward

propagating Alfvén waves and assess their contribution to the total auroral emission, the space physics community has pursued a combination of spacecraft conjunction studies and statistical

studies of the spatial distribution of Alfvén waves and precipitating electrons. Measurements from the Polar spacecraft at altitudes \(3\,{\rm{{R}}_{E}}\, \lesssim\, z\, \lesssim\,

6\,{\rm{{R}}_{E}}\) (Earth radii) show that the downward Poynting flux of Alfvén waves was sufficient to power the intense auroral emission observed at magnetically conjugate points in the

ionosphere14,15. Subsequent conjunction studies between Polar or Cluster at \(z\, \gtrsim\, 4\,{\rm{{R}}_{E}}\) and FAST below at \(z \sim 0.5\,{\rm{{R}}_{E}}\) showed a transition from

downward Alfvén Poynting flux at high altitudes to significant precipitating energetic electron flux at lower altitudes5,16,17, suggesting that Alfvén wave energy is lost through the

acceleration of electrons over the intervening altitude range. Although the electron acceleration is generally thought to occur over the altitude range \(1\,{\rm{{R}}_{E}}\, \lesssim\, z\,

\lesssim\, 2\,{\rm{{R}}_{E}}\)18,19, sorting Alfvén Poynting flux by altitude shows a significant drop in amplitude over \(3\,{\rm{{R}}_{E}}\, \lesssim\, z\, \lesssim\,

4\,{\rm{{R}}_{E}}\)20. This fundamental picture of auroral electron acceleration by Alfvén waves also appears relevant to other planetary magnetospheres, with recent Juno measurements

showing Alfvénic fluctuations associated with auroral emissions at Jupiter21. Statistical studies of the spatial distribution of Alfvén wave power and precipitating electron flux using FAST

and Polar measurements have shown that the spatial distribution in magnetic local time and latitude of Alfvén wave Poynting flux is well correlated with the distribution of accelerated

electrons and the auroral emission22,23,24, with modeling suggesting the accelerated electrons primarily arrive from an altitude of \(2\,{\rm{{R}}_{E}}\, \lesssim\, z\,\lesssim\,

3\,{\rm{{R}}_{E}}\)22. Furthermore, the Alfvén wave Poynting flux was found to be sufficient to power ~1/3 of the global auroral luminosity, and up to 50% in the pre-midnight sector where

substorm driven auroral events occur23,24, and Alfvén waves may be the dominant mechanism of electron acceleration during geomagnetic storms20,25,26. Together, these conjunction and

statistical studies build a strong case for the Alfvén-wave acceleration of auroral electrons. To develop a complete physical understanding of this critical element of

magnetosphere-ionosphere coupling, it is essential to identify the kinetic plasma physics governing the acceleration of electrons by Alfvén waves. Analytical considerations and numerical

modeling have framed the basic kinetic physics involved. Over the auroral acceleration region from \(1\,{\rm{{R}}_{E}}\,\lesssim \,z\,\lesssim\, 3\,{\rm{{R}}_{E}}\), the Earth’s relatively

high magnetic field _B_0 and low plasma electron density _n__e_ and temperature _T__e_ lead to conditions in the inertial regime, characterized by an Alfvén velocity greater than the

electron thermal velocity, _v__A_ > _v__t__e_27,28. The Alfvén waves measured in the auroral acceleration region have typical length scales perpendicular to the magnetic field B0 that are

comparable to the electron skin depth. Unlike the Alfvén waves of ideal MHD29, inertial Alfvén waves under these conditions are dispersive and give rise to an electric field component

parallel to B028,30. It is proposed that the parallel electric field of these waves can accelerate the precipitating electrons that power the aurora13,28,31. Kletzing32 mapped a distribution

of test particles through prescribed inertial Alfvén wave fields and found electrons can be accelerated to auroral energies through a process similar to single-bounce Fermi acceleration

where electrons gain energy while being overtaken by the wave and then are accelerated out of the front of the wave. Additional tests with realistic altitude profiles of the plasma

parameters indicated that auroral electrons could be resonantly accelerated by inertial Alfvén waves33,34. It is scientifically desirable to confirm definitively the kinetic physics of

Alfvénic electron acceleration by simultaneously measuring the Alfvén wave fields and the resulting changes to the electron velocity distribution. Both measurements are essential to diagnose

directly the transfer of energy between the waves and electrons. Spacecraft measurements, suffering uncertainty from plasma inhomogeneity, field line mapping, spacecraft motion, and limited

points of measurement, have not been able to provide such a direct test. In this work, we overcome the inherent limitations of spacecraft measurements by performing laboratory experiments35

on the Large Plasma Device (LAPD), a joint National Science Foundation/Department of Energy user facility at UCLA36. Inertial Alfvén waves are launched in the LAPD plasma and measurements

of the electron velocity distribution are simultaneously collected using the absorption of a small amplitude whistler-mode wave. An analysis of measurements using the field-particle

correlation technique gives a velocity-space signature indicating electrons are resonantly accelerated by inertial Alfvén waves in the experiment. Analytical kinetic theory, numerical

Liouville mapping of a test particle distribution, and nonlinear gyrokinetic simulation are consistent with data from the experiment. The energy gain per electron per second in the

experiment is consistent with an estimation using parameters from the auroral zone. While it was previously known that Alfvén waves are often coincident with auroras, this direct measurement

demonstrates a causal relationship between Alfvén waves and accelerated electrons that produce auroras. RESULTS The LAPD is a 20 m long, 1 m diameter cylindrical vacuum chamber with a

strong axial magnetic field of \({{\bf{B}}}_{0}=0.1700\hat{{\bf{z}}}\) T. While the characteristic parameters (magnetic field, density, and temperature) of the LAPD experiments differ by

orders of magnitude from those in the auroral magnetosphere, a similarity analysis can be exploited to demonstrate that the key dimensionless parameters governing the physics of auroral

electron acceleration can be reproduced in the laboratory35,37. The key condition determining the acceleration of auroral electrons is that the ratio of the electron thermal velocity to the

Alfvén velocity is less than unity, _v__t__e_/_v__A_ < 1. Our experiments achieve a ratio _v__t__e_/_v__A_ = 0.35 such that the parallel resonant velocity of inertial Alfvén waves falls

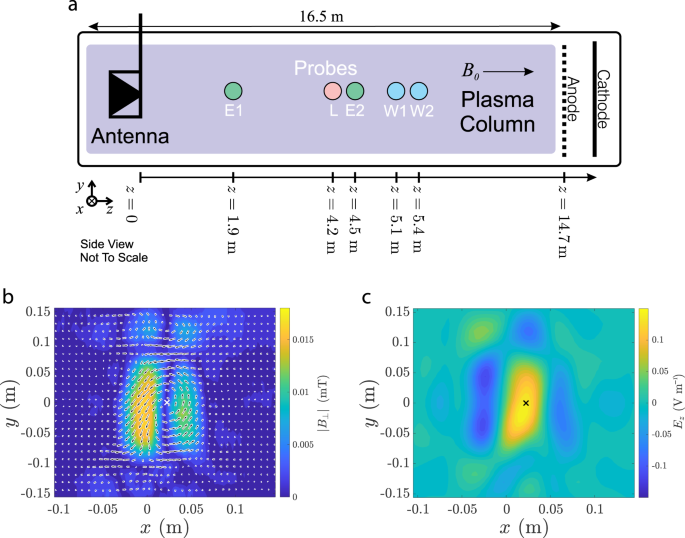
in the suprathermal tail of the electron distribution (Supplementary Methods 1). ALFVÉN WAVE MEASUREMENTS We use the specially designed Sigma antenna to launch inertial Alfvén waves from one

end of the chamber, as shown in Fig. 1a, Elsässer probes38 to record the electromagnetic fields, and a Whistler Wave Absorption Diagnostic (WWAD)39 to make simultaneous measurements of the

parallel electron velocity distribution40,41,42,43 (see Methods for more detail on the experimental setup and procedure). The propagation of Alfvén waves between probes E1 and E2 is found to

agree with the inertial Alfvén wave dispersion relation that includes the effects of thermal collisions (Supplementary Methods 2). In Fig. 1, over the plane (_x_, _y_) perpendicular to the

axial magnetic field, we show (b) the measured Alfvén wave field B⊥ at E2 and (c) the predicted parallel electric field _E__z_ at the WWAD, calculated using B⊥ and Ampére’s law

(Supplementary Methods 2). The (_x_, _y_) position of the electron velocity distribution function measurement using the WWAD is indicated in Fig. 1b, c by the _x_, chosen at a maximum of the

Alfvén wave _E__z_, i.e. a current channel. DISTRIBUTION FUNCTION MEASUREMENTS High-precision measurements of the suprathermal tails of the parallel electron velocity distribution

_g__e_(_v__z_) were performed using the WWAD39,40,41,42,43. This measurement technique provides sufficient time resolution and precision to determine variations of _g__e_(_v__z_) as the

Alfvén wave phase advances44 (Supplementary Methods 3). The wave absorption technique is unable to provide measurements of _g__e_(_v__z_) through the lower-velocity bulk of the distribution;

however, because resonant acceleration affects suprathermal electrons, we are still able to explore this phenomenon with the available measurements (Supplementary Methods 3). In Fig. 2a, we

show the background distribution _g__e_0(_v__z_), obtained from a Fourier transform of distribution function measurements over the Alfvén wave period _T_ = 2_π_/_ω_, where the contribution

from the _n_th Fourier harmonic is given by _g__e__n_(_v__z_, _t_). Each side of _g__e_0(_v__z_) is fitted with a two-temperature Maxwellian distribution (red): a dominant, cold thermal core

consistent with the Langmuir probe measurements of _T__e_ and a hotter, diffuse component. The hotter 60 eV population seen for _v__z_ < 0 corresponds to the energy of the primary

electrons accelerated across the cathode-anode potential drop of the plasma source. In Fig. 2b, we plot measurements of the total perturbation _δ__g__e_(_v__z_) = _g__e_(_v__z_) − 

_g__e_0(_v__z_) over 2_π_ of Alfvén wave phase, showing a signal along the vertical axis dominated by the fundamental mode of oscillations _g__e_1(_v__z_) at the frequency _ω_ of the Alfvén

wave. A previously derived analytical solution to the linearized Boltzmann equation44,45, shown in Fig. 2c, reproduces the dominant features of this pattern using only _g__e_1(_v__z_). While

the linear solution to the Boltzmann equation includes a velocity-dependent Coulomb collision rate, the typical suprathermal electron will travel nearly collisionlessly through the length

of the experiment (Supplementary Methods 1). The upward slant of the blue and red features in the _v__z_ > 0 region of Fig. 2b, c indicates phase variation in the response of

_g__e_(_v__z_) to the Alfvén wave, i.e. faster electrons are not oscillating with the same phase relative to the Alfvén wave as slower electrons. As we will show, this difference in phase

means that in some regions of velocity space the electrons gain energy, while in other regions they lose energy, ultimately producing a signature characteristic of resonant energy

transfer46,47,48. FIELD-PARTICLE CORRELATION OF EXPERIMENTAL DATA Using single-point measurements of the electric field and electron velocity distribution, the rate of energization of

electrons as a function of their velocity in the experiment is diagnosed using the field-particle correlation technique46,47,48 (Supplementary Methods 4). To determine the net rate of work

done by _E__z_ on the electrons, we use the measured _g__e_1(_v__z_, _t_) and _E__z_(_t_) to compute the parallel field-particle correlation, defined by $${C}_{{E}_{z}}({v}_{z})={\rm{Corr}}\

\left(\frac{e{v}_{z}^{2}}{2}\frac{\partial {g}_{e1}({v}_{z},t)}{\partial {v}_{z}},{E}_{z}(t)\right),$$ (1) where this unnormalized correlation is an average of the product of the terms over

one full Alfvén wave period. This correlation \({C}_{{E}_{z}}({v}_{z})\) yields the rate of change of parallel phase-space energy density,

\({w}_{e}({v}_{z})={m}_{e}{v}_{z}^{2}{g}_{e}({v}_{z})/2\), as a function of the parallel velocity _v__z_ attributable to the interaction of electrons with the Alfvén wave field _E__z_. Key

features of the field-particle correlation as a function of _v__z_, such as regions where \({C}_{{E}_{z}}({v}_{z})\) is positive or negative as well as the location of zero crossings, are

referred to collectively as the velocity-space signature, and can be compared to the velocity-space signatures of known wave-particle interactions. Applying the field-particle correlation to

the measured _g__e_1(_v__z_) gives \({C}_{{E}_{z}}({v}_{z})\) shown in Fig. 3a, where the vertical line around 24 eV shows the energy corresponding to the parallel wave phase velocity

_v__z_ = _v__p__h_. The transition of \({C}_{{E}_{z}}({v}_{z})\) from negative to positive indicates the energy density of the electron distribution is decreasing at lower velocities and

increasing at higher velocities. Changes in the phase-space energy density _w__e_(_v__z_) occur only when the number of particles at a given velocity _v__z_ changes. For example, when

electrons are accelerated to a higher velocity, _w__e_(_v__z_) decreases at their initial lower velocity and increases at their final higher velocity. This produces a bipolar signature in

\({C}_{{E}_{z}}({v}_{z})\)—negative at the lower velocity, and then crossing through zero and becoming positive at the higher velocity. Using this insight to provide a physical

interpretation of Fig. 3a, electrons are being moved within the distribution from lower velocity to higher velocity by the Alfvén wave. This is direct experimental evidence for the

acceleration of electrons by inertial Alfvén waves. For help identifying the wave-particle interaction responsible for the electron acceleration detected experimentally, we turn to

analytical theory and numerical simulation. COMPARISON TO NUMERICAL SIMULATIONS AND ANALYTICAL THEORY To interpret the experimental \({C}_{{E}_{z}}({v}_{z})\), we begin by comparing the

experimental \({C}_{{E}_{z}}({v}_{z})\) with a nonlinear gyrokinetic simulation of inertial Alfvén waves (Supplementary Methods 5). The electromagnetic fields and velocity distributions of

ions and electrons of a simulated plasma are self-consistently advanced assuming the distributions are gyrotropic, or particles are performing uniform circular motion around the magnetic

field. Using plasma parameters relevant to the experiment, we initialize an inertial Alfvén wave in a periodic domain and use the resulting electron velocity distribution and _E__z_(_t_) of

the inertial Alfvén wave at a single point to compute \({C}_{{E}_{z}}\) in Fig. 3b shown in gyrotropic velocity space (_v__z_, _v_⊥) and (c) reduced to _v__z_. Gyrokinetic results are

presented in the typical way with axes showing velocity normalized to the electron thermal speed. The gyrokinetic \({C}_{{E}_{z}}({v}_{z})\), bipolar with a zero crossing at _v__p__h_, is

the known velocity-space signature of electron acceleration via Landau damping48. This wave-particle interaction can be interpreted physically as electrons being accelerated by the wave to

velocities greater than the wave itself, similar to how a surfer can end up traveling faster than the crest of the ocean wave. The gyrokinetic result is not unexpected since test particle

simulations have predicted inertial Alfvén waves accelerate electrons via Landau resonance32,33,34. Although gyrokinetic results in Fig. 3b, c are presented using velocity axes conventional

for gyrokinetic simulation while experimental results in (a) are plotted using an energy axis, key similarities and differences are evident. Like the gyrokinetic result, the experimental

\({C}_{{E}_{z}}({v}_{z})\) is also bipolar. Unlike the gyrokinetic result, the zero crossing of the experimental \({C}_{{E}_{z}}({v}_{z})\) falls below _v__p__h_. This discrepancy between

the zero crossing of the experimental \({C}_{{E}_{z}}({v}_{z})\) and the wave phase velocity is explained by accounting for the finite distance of the experimental measurement from the

antenna. To model this effect, we have analytically solved the linearized Boltzmann equation using a Laplace transform for an inertial Alfvén wave generated at _z_ = 0 (Supplementary Methods

 6). The analytical solution allows us to predict in Fig. 3d how \({C}_{{E}_{z}}({v}_{z})\) varies as a function of distance _z_ from the Alfvén wave antenna, where the vertical axis is

normalized by the parallel wavelength, _z_/_λ__z_. Figure 3d helps interpret both the gyrokinetic and the experimental \({C}_{{E}_{z}}({v}_{z})\). With its periodic domain, the gyrokinetic

simulation in (c) effectively has a long interaction length, making it most comparable to the largest values of _z_/_λ__z_ in (d), where indeed we find that the zero crossing of the

velocity-space signature falls at _v__p__h_. Conversely, the experimental \({C}_{{E}_{z}}({v}_{z})\) in (a) is measured near _z_/_λ__z_ ≃ 2, and we see in (d) that the zero crossing of the

velocity-space signature at that position is predicted to fall below the phase velocity, as observed in the experiment. A slice along _z_/_λ__z_ ≃ 2 (dashed horizontal line) in (d) is

plotted in (e), showing that, near the antenna, the zero crossing of \({C}_{{E}_{z}}({v}_{z})\) occurs at a velocity below the wave phase velocity, _v__z_ < _v__p__h_. Note that the data

in panel (e) is the same data as the model results (red) plotted in panel (a), so the theoretical prediction of \({C}_{{E}_{z}}({v}_{z})\) yields quantitative agreement with the experiment.

Physically, the signature of the zero crossing of \({C}_{{E}_{z}}({v}_{z})\) falling below the resonant velocity is due to electrons originating at _z_ = 0 that start below _v__p__h_ being

resonantly accelerated but having not yet reached their maximum velocity _v__z_ ≳ _v__p__h_. Together, these results form a consistent picture that the velocity-space signature arising from

the Landau resonance evolves as resonant electron acceleration unfolds over a finite distance _z_ from the antenna. While the gyrokinetic simulation is not well-suited to finite interaction

lengths, a mapping of phase space through the predicted wave fields according to Liouville’s theorem is an established technique32,33 that is capable of modeling finite length interactions.

Liouville mapping provides an independent approach to determine if indeed the zero crossing of \({C}_{{E}_{z}}({v}_{z})\) falls below _v__p__h_ as suggested by analytical theory in Fig. 3d

when the distance from the antenna is _z_/_λ__z_ ≃ 2. In Fig. 3f, we present the gyrotropic field-particle correlation from such a Liouville mapping (Supplementary Methods 7), and there are

signs of agreement with the experimental \({C}_{{E}_{z}}({v}_{z})\). In (f), we see the expected bipolar velocity-space signature characteristic of the Landau resonant acceleration, but, in

agreement with the analytical prediction, the zero crossing falls below _v__p__h_ due to the finite distance _z_/_λ__z_ ≃ 2 from the antenna. Integrating over _v_⊥ yields (g) a reduced

parallel velocity-space signature that makes clear these distinguishing features. To enable a more direct comparison to the experimental results, we convert the horizontal axis of (g) from

parallel velocity _v__z_ to the associated energy, as shown in Fig. 3h. This final Liouville mapping prediction shows qualitative agreement with our experimental determination of

\({C}_{{E}_{z}}({v}_{z})\). The discrepancy in magnitude between Fig. 3a and h is attributed largely to the fact that Liouville mapping includes only the dominant plane wave mode present in

the launched Alfvén wave in Fig. 1, neglecting all harmonics present in the experiment (Supplementary Methods 8). But, the quantitative agreement of the zero crossing in the bipolar

velocity-space signature of \({C}_{{E}_{z}}({v}_{z})\) between (a) the experiment and (h) the Liouville mapping model definitively identifies the Landau resonance as the mechanism of

electron acceleration. The discrepancy in magnitude does not suggest an alternate acceleration mechanism is at work. The agreement between the experimentally determined

\({C}_{{E}_{z}}({v}_{z})\) and the various model results confirm that we have experimentally identified resonant energy transfer from inertial Alfvén waves to electrons. CONNECTION TO AN

ACCELERATED BEAM OF ELECTRONS The measurements presented above demonstrate a resonant energy transfer rate between inertial Alfvén waves and electrons. Over an extended interaction region

like the auroral zone, the cumulative effect of this energy transfer is a population of accelerated electrons. For the relatively short distance of interaction between the antenna and the

point of measurement in the experiment (about two wavelengths), the resulting component of accelerated electrons may not be easily discernible. By extending the distance of the Liouville

mapping calculation, we show that the experimentally detected energy transfer rate applied over a longer interaction region does indeed generate an accelerated population of electrons

(Supplementary Methods 7). In Fig. 4, we plot the predicted gyrotropic electron velocity distribution (a) at the point of measurement at _z_ = 5.27 m, or _z_/_λ__z_ ≃ 2, and (b) at a

distance five times further (over 10 m beyond the end of the LAPD experimental chamber) at _z_ = 26.3 m, _z_/_λ__z_ ≃ 10. Although the effect of the acceleration of electrons by the inertial

Alfvén wave is difficult to discern at _z_/_λ__z_ ≃ 2 by looking at the distribution function alone, by the time the wave reaches _z_/_λ__z_ ≃ 10, the population of accelerated electrons

would be clearly observed, with an accelerated beam reminiscent of early auroral acceleration modeling32. The resonant velocity (black solid) and nonlinear trapping width49 for the

experimental wave amplitude (gray dashed) are indicated, showing a significant net acceleration of electrons within the nonlinear trapping width, as expected theoretically. While measuring

an accelerated population of electrons experimentally, for example by detecting a beam in the electron distribution far from the antenna, would provide supporting evidence for our

conclusions, this measurement alone would not be sufficient to prove that we have observed electrons accelerated by an inertial Alfvén wave. A population of accelerated electrons can be

produced by a number of nonlinear effects that may arise while launching high-power waves in laboratory plasmas. Conversely, the field-particle correlation allows the specific conclusion

that energy is being transferred to electrons from the Alfvén wave, and the bipolar signature and its zero crossing make clear the responsible acceleration mechanism is the Landau resonance.

CONNECTION TO THE AURORAL ACCELERATION REGION We may compare the rate of energization of electrons by the inertial Alfvén wave in this experiment with a comparable case in the auroral

acceleration region of the magnetosphere. The number density of accelerated electrons _n__a__c__c_ is computed by directly integrating the equilibrium distribution function _g__e_0(_v__z_)

over the range of velocities where significant energization occurs, from _v__z_,_m__i__n_/_v__t__e_ = 1.96 (corresponding to our lower cutoff at 15.5 eV) to _v__z_,_m__a__x_/_v__t__e_ = 3.18

(or 40.6 eV), yielding _n__a__c__c_ = 1.59 × 1015 m−3. Similarly, integrating the parallel field-particle correlation \({C}_{{E}_{z}}({v}_{z})\) over the same velocity limits yields the net

rate of energy transfer to these accelerated electrons (_d__E_/_d__t_)_a__c__c_ = 20.6 J m−3 s−1. To find the average rate of energization per electron, we can divide these two numbers to

obtain an energization rate of 8.1 × 104 eV s−1 per electron. To make a meaningful comparison to the rate of energization per electron in the auroral acceleration region, we have developed a

model (Supplementary Methods 9) of the plasma parameters as a function of distance along a magnetic field line given by _L_ = 8.5, or invariant latitude _λ_ = 70∘. In Fig. 5, we show (a)

the inner magnetosphere’s dipolar magnetic field lines (blue) in Geocentric Solar Magnetospheric coordinates, and we highlight (red) the segment along the _L_ = 8.5 field line from an

altitude _z_ = 1000 km. We also show (b) the profiles of Alfvén velocity _v__A_ (red) and electron thermal velocity _v__t__e_ (blue) vs. distance along the field line _s_ from the Earth’s

surface (measured in units of the Earth radii, \(\,{\rm{{R}}_{E}}\)). We also plot (c) the ratio _v__A_/_v__t__e_ vs. _s_, where the region corresponding to our experimental parameters with

_v__A_/_v__t__e_ ≃ 3 is highlighted (red). During magnetospheric substorms, when Alfvén waves are believed to drive a significant fraction of the observed discrete auroral arcs24, shifts in

the magnetic field within the distant magnetotail (possibly due to magnetotail reconnection) are transmitted Earthward along the magnetic field as Alfvén waves12,28. In Fig. 5b, at distances

along the field line \(s\, \gtrsim\, 3.5\,{\rm{{R}}_{E}}\), the plasma is in the regime of kinetic Alfvén waves where _v__t__e_ > _v__A_, and therefore the parallel electron velocity

that is resonant with the parallel phase velocity of Alfvén and kinetic Alfvén waves falls within the core of the electron velocity distribution at _v__z_ < _v__t__e_. In this case,

resonantly damped wave energy is likely to be shared among the large population of these core electrons, and so the resonant interaction may lead to a broadening of the velocity distribution

in the parallel direction, but may not be as effective in accelerating electrons to high energies. It should be mentioned, however, that several numerical studies have suggested that

trapping of electrons in finite-amplitude kinetic Alfvén waves or kinetic-scale field-line resonances may be effective at accelerating electrons to keV energies50,51,52 in this regime at

altitudes \(z\, > \, 4\,{\rm{{R}}_{E}}\). At distances \(s\, \lesssim\, 3.5\,{\rm{{R}}_{E}}\) in Fig. 5b, the plasma is in the regime of inertial Alfvén waves where _v__A_ > _v__t__e_,

so the resonant parallel electron velocity falls within the suprathermal tail of the electron velocity distribution, _v__z_ > _v__t__e_. In this case, the resonantly damped wave energy

is shared by only the small population of electrons in the tail, and these electrons may be more effectively accelerated to higher energies. In fact, since the Alfvén wave velocity is

observed to increase as _s_ decreases over the range \(1\,{\rm{{R}}_{E}}\, \lesssim\, s\,\lesssim\, 3.5\,{\rm{{R}}_{E}}\), accelerated electrons can stay resonant with these accelerating

Alfvén waves as they propagate toward the Earth, enabling these electrons to reach keV energies (where the horizontal dotted line indicates the parallel velocity of an electron with 1 keV of

kinetic energy)32,33. It is this range of distances along the field line, which corresponds in our model to altitudes \(1\,{\rm{{R}}_{E}}\, \lesssim\, z\,\lesssim\, 3\,{\rm{{R}}_{E}}\),

that is traditionally denoted the auroral acceleration region (green horizontal line)53. To compare the average rate of energization of resonant electrons in the auroral acceleration region,

we use the plasma parameters from the auroral acceleration region model (Supplementary Methods 9) to compute the number density of acceleration electrons _n__a__c__c_ and the rate of change

of energy density (_d__E_/_d__t_)_a__c__c_ at the comparable point (with _v__A_/_v__t__e_ ≃ 3) along the field line at \(s\simeq 2.85\,{\rm{{R}}_{E}}\), corresponding to an altitude

\(z\simeq 2.56\,{\rm{{R}}_{E}}\). At this point, the model yields plasma parameters _B_0 = 1140 nT, _n__e_ = 4 × 106 m−3, and _T__e_ = 50 eV. The number density of electrons that are

resonant with the Alfvén wave are estimated by integrating a Maxwellian electron velocity distribution over the same normalized limits as the experiment, _v__z_,_m__i__n_/_v__t__e_ = 1.96

and _v__z_,_m__a__x_/_v__t__e_ = 3.18. We obtain _n__a__c__c_ ≃ _n__e_ erfc(1.96) = 0.0036_n__e_ = 1.44 × 104 m−3, where erfc denotes the complementary error function. The rate of transfer

of energy density from the inertial Alfvén wave to these resonant electrons is estimated using the linear collisionless damping rate _γ_ and wave magnetic energy density for these

parameters, \({(dE/dt)}_{acc}=2\gamma {(\delta {B}_{\perp })}^{2}/2{\mu }_{0}\). For the plasma parameters _v__A_/_v__t__e_ = 3 and _T__i_/_T__e_ = 1, the linear Vlasov-Maxwell dispersion

relation54,55 yields a normalized complex wave frequency _ω_/_k_∥_v__A_ = (0.795, − 1.5 × 10−2) for a wave with _k_⊥_δ__e_ = 1, the typical perpendicular scale where the inertial Alfvén wave

parallel electric field leads to resonant energization via the Landau resonance. For an estimated parallel wavelength of _L_∥ ~ 500 km and a wave amplitude at this altitude of _δ__B_⊥ ~ 10 

nT, we obtain a energization rate of (_d__E_/_d__t_)_a__c__c_ = 1.9 × 10−10 J m−3 s−1. Dividing these two numbers to obtain the average rate of energization per electron, we obtain 8.2 × 104

 eV s−1 per electron. Uncertainty in our estimated value of the parallel wavelength _L_∥ and the use of an idealized Maxwellian equilibrium velocity distribution mean that this energization

rate is only an order-of-magnitude estimate, but this value is clearly consistent with that found in the experiment. By designing a scaled laboratory experiment to obtain the same key

dimensionless parameter _v__A_/_v__t__e_ ≃ 3, we have shown that the energization rate per electron by the inertial Alfvén wave agrees with the prediction for the auroral acceleration

region. DISCUSSION Early calculations by Kletzing32,33 predicted that, for realistic auroral acceleration region parameters, Alfvén wave acceleration can account for the quantitative

features of precipitating auroral electrons. While this hypothesis is consistent with spacecraft measurements in auroral regions, it has not previously been directly tested. In this

experiment, measured changes to the electron velocity distribution, when correlated with the Alfvén wave fields, indicate resonant electron acceleration. The same acceleration process is

seen while modeling inertial Alfvén wave-particle interactions with gyrokinetic simulation, analytical theory, and Liouville mapping. Experimental results are reproduced by analytical theory

and Liouville mapping once the finite length of the experiment is included. The experimental field-particle correlation, and its agreement with analytical theory and Liouville mapping,

allow the specific conclusion that the inertial Alfvén wave in this experiment is accelerating electrons and that the responsible acceleration mechanism is Landau resonance. By extending

Liouville mapping calculations over a longer interaction length, we show that the cumulative effect of the energy transfer detected in this experiment is the production of a distinct

population of accelerated electrons. The agreement of the rate of energization per electron between the experiment and an auroral model at altitude \(z \sim 2.5\,{\rm{{R}}_{E}}\) establishes

the final connection needed to show we have provided direct experimental confirmation that Alfvén waves can accelerate electrons that precipitate into the ionosphere and generate the

fascinating glow of the aurora. METHODS The LAPD chamber is backfilled with H2 to 10−5 Torr. A heated nickel cathode, coated with barium oxide to lower the work function, emits primary

electrons from one end of the vacuum vessel, shown in Fig. 1a, that collisionally dissociate and ionize the H2 fill gas, producing a plasma with electron density _n__e_ = (1.2 ± 0.2) × 1018 

m−3 and _T__e_ = 4 ± 1 eV. Electron density and temperature are determined using a swept Langmuir probe, and absolute calibration of the density measurement is obtained using a microwave

interferometer. Measured experimental parameters, derived characteristic plasma scales, and key dimensionless quantities of the experiment are presented in Supplementary Table 1. The LAPD

produces a 10 ms shot of plasma every second. Data from several shots show the plasma is reproducible from shot to shot. During each shot, a burst of traveling inertial Alfvén waves is

launched at a fixed moment in the discharge sequence by our Sigma antenna at a frequency of 1.177 MHz. The Alfvén wave fields B⊥ and E⊥, perpendicular to B0, are recorded using Elsässer

probes38 at a distance of \(1.9\hat{{\bf{z}}}\) and \(4.5\hat{{\bf{z}}}\) m from the Alfvén wave antenna. During each shot, each Elsässer probe provides measurements at a single location

(_x_, _y_, _z_). Shot-to-shot fluctuations of the plasma conditions and Alfvén wave fields are normally distributed, and 10 shots of Elsässer probe data at a given location provides a

sufficient signal-to-noise ratio to record the local temporal evolution of B⊥ and E⊥. Elsässer probes are mounted to an automated motion system so that 10 shots of data are collected at each

point of a user-defined grid in the _x_–_y_ plane. Additional properties of the Sigma antenna and the resulting inertial Alfvén waves are given in Supplementary Methods 2. The WWAD39

provides high-precision measurements of the suprathermal tails of the reduced parallel electron velocity distribution _g__e_(_v__z_) at an approximately localized position in configuration

space. The diagnostic is implemented with 1" dipole antennas, denoted as W1 and W2 in Fig. 1a, that are used as a transmitter and receiver separated by \({{\Delta

}}z=0.3\hat{{\bf{z}}}\) m. Because _g__e_(_v__z_) is measured using the absorption of whistler waves between the dipole antennas, the measured _g__e_(_v__z_) is an average over the distance

separating the antennas. However, the spacing of the WWAD antennas is much less than the Alfvén parallel wavelength, Δ_z_/_λ__z_ = 0.12, so the measured _g__e_(_v__z_) is approximately local

compared to the Alfvén wave. Measurements of _g__e_(_v__z_) are performed near (_x_, _y_, _z_) = (0.02, 0.00, 5.25) m. The _x_ and _y_ coordinates, marked by an _x_ in Fig. 1b, c, were

chosen because they are revealed by Elsässer probe measurements to be a maximum of E_z_, and therefore this location is also a maximum of the perturbation to _g__e_(_v__z_) caused by the

Alfvén wave. The WWAD measures _g__e_(_v__z_) with 10 μs resolution. To resolve the 0.85 μs period of the Alfvén wave, a series of 32 phase-shifted data sets is collected, where each data

set consists of 1024 shots. Before each data set, the launch of the Alfvén wave burst is delayed by an additional 1/32 of the Alfvén wave period. Every time step in the measurement of

_g__e_(_v__z_) is sorted into a grid indexed by electron velocity _v__z_ and \({\phi }_{{E}_{z}}\) the phase of the Alfvén wave’s parallel electric field _E__z_. Alfvén wave phase is

determined from Elsässer probe measurements of the Alfvén wave fields detailed in Supplementary Methods 2. Additional information about measuring _g__e_(_v__z_) using the WWAD is provided in

Supplementary Methods 3. DATA AVAILABILITY The numerical simulations presented here are available from the corresponding author upon reasonable request. LAPD data are managed by the Basic

Plasma Science Facility at UCLA (https://plasma.physics.ucla.edu) and are available from the Facility upon reasonable request. CODE AVAILABILITY All relevant AstroGK code and Matlab routines

are available from the corresponding author upon reasonable request. AstroGK source code is available from https://bitbucket.org/gyrokinetics/. REFERENCES * Hapgood, M. Astrophysics:

prepare for the coming space weather storm. _Nature_ 484, 311–313 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Akasofu, S. I. The auroral oval, the auroral substorm, and their

relations with the internal structure of the magnetosphere. _Planet. Space Sci._ 14, 587–595 (1966). Article  ADS  Google Scholar  * McIlwain, C. E. Direct measurement of particles producing

visible auroras. _J. Geophys. Res._ 65, 2727 (1960). Article  ADS  Google Scholar  * Meng, C. I. & Lundin, R. Auroral morphology of the midday oval. _J. Geophys. Res._ 91, 1572–1584

(1986). Article  ADS  Google Scholar  * Schriver, D. et al. FAST/Polar conjunction study of field-aligned auroral acceleration and corresponding magnetotail drivers. _J. Geophys. Res._ 108,

8020 (2003). Article  Google Scholar  * Eastman, T. E., Hones, J. E. W., Bame, S. J. & Asbridge, J. R. The magnetospheric boundary layer: Site of plasma, momentum and energy transfer

from the magnetosheath into the magnetosphere. _Geophys. Res. Lett._ 3, 685–688 (1976). Article  ADS  Google Scholar  * Kennel, C. F. & Petscheck, H. E. Limit on stably trapped particle

fluxes. _J. Geophys. Res._ 71, 1–28 (1966). Article  ADS  Google Scholar  * Kennel, C. F. Consequences of a magnetospheric plasma. _Rev. Geophys. Space Phys._ 7, 379–419 (1969). Article  ADS

  Google Scholar  * Iijima, T. & Potemra, T. A. Field-aligned currents in the dayside cusp observed by triad. _J. Geophys. Res._ 81, 5971–5979 (1976). Article  ADS  Google Scholar  *

Cowley, S. W. H. TUTORIAL: magnetosphere-ionosphere interactions: a tutorial review. _Wash. DC Am. Geophys. Union Geophys. Monograph. Series_ 118, 91 (2000). ADS  Google Scholar  * Samson,

J. C. et al. Observations of a detached, discrete arc in association with field line resonances. _J. Geophys. Res._ 96, 15683–15695 (1991). Article  ADS  Google Scholar  * Hasegawa, A.

Particle acceleration by MHD surface wave and formation of aurora. _J. Geophys. Res._ 81, 5083–5090 (1976). Article  ADS  Google Scholar  * Goertz, C. K. & Boswell, R. W.

Magnetosphere-ionosphere coupling. _J. Geophys. Res._ 84, 7239–7246 (1979). Article  ADS  Google Scholar  * Wygant, J. R. et al. Polar spacecraft based comparisons of intense electric fields

and Poynting flux near and within the plasma sheet-tail lobe boundary to UVI images: an energy source for the aurora. _J. Geophys. Res._ 105, 18 (2000). Google Scholar  * Keiling, A. et al.

Correlation of Alfvén wave Poynting flux in the plasma sheet at 4-7 R_E_ with ionospheric electron energy flux. _J. Geophys. Res._ 107, 1132 (2002). Article  Google Scholar  * Chaston, C.

C. et al. Energy deposition by Alfvén waves into the dayside auroral oval: Cluster and FAST observations. _J. Geophys. Res. Space Phys._ 110, A02211 (2005). Article  ADS  CAS  Google Scholar

  * Dombeck, J., Cattell, C., Wygant, J. R., Keiling, A. & Scudder, J. Alfvén waves and Poynting flux observed simultaneously by Polar and FAST in the plasma sheet boundary layer. _J.

Geophys. Res._ 110, A12S90 (2005). ADS  Google Scholar  * Mizera, P. F. & Fennell, J. F. Signatures of electric fields from high and low altitude particles distributions. _Geophys. Res.

Lett._ 4, 311–314 (1977). Article  ADS  CAS  Google Scholar  * Ghielmetti, A. G., Johnson, R. G., Sharp, R. D. & Shelley, E. G. The latitudinal, diurnal, and altitudinal distributions of

upward flowing energetic ions of ionospheric origin. _Geophys. Res. Lett._ 5, 59–62 (1978). Article  ADS  CAS  Google Scholar  * Janhunen, P., Olsson, A., Russell, C. T. & Laakso, H.

Alfvénic electron acceleration in aurora occurs in global Alfvén resonosphere region. _Space Sci. Rev._ 122, 89–95 (2006). Article  ADS  Google Scholar  * Gershman, D. J. et al. Alfvénic

fluctuations associated with Jupiter’s Auroral EMissions. _Geophys. Res. Lett._ 46, 7157–7165 (2019). Article  ADS  Google Scholar  * Chaston, C. C. et al. Properties of small-scale Alfvén

waves and accelerated electrons from FAST. _J. Geophys. Res._ 108, 8003 (2003). Article  Google Scholar  * Keiling, A., Wygant, J. R., Cattell, C. A., Mozer, F. S. & Russell, C. T. The

global morphology of wave poynting flux: powering the aurora. _Science_ 299, 383–386 (2003). Article  ADS  CAS  PubMed  Google Scholar  * Chaston, C. C., Carlson, C. W., McFadden, J. P.,

Ergun, R. E. & Strangeway, R. J. How important are dispersive Alfvén waves for auroral particle acceleration? _Geophys. Res. Lett._ 34, 7101 (2007). Article  ADS  Google Scholar  *

Keiling, A., Thaller, S., Wygant, J. & Dombeck, J. Assessing the global Alfvén wave power flow into and out of the auroral acceleration region during geomagnetic storms. _Science

Advances_ 5, eaav8411 (2019). Article  ADS  PubMed  PubMed Central  Google Scholar  * Keiling, A., Thaller, S., Dombeck, J. & Wygant, J. Temporal evolution of substorm-driven global

Alfvén wave power above the auroral acceleration region. _J. Geophys. Res._ 125, e27444 (2020). Article  ADS  Google Scholar  * Kletzing, C. A., Mozer, F. S. & Torbert, R. B. Electron

temperature and density at high latitude. _J. Geophys. Res._ 103, 14837–14846 (1998). Article  ADS  Google Scholar  * Stasiewicz, K. et al. Small scale Alfvénic structure in the aurora.

_Space Sci. Rev._ 92, 423–533 (2000). Article  ADS  Google Scholar  * Alfvén, H. Existence of electromagnetic-hydrodynamic waves. _Nature_ 150, 405–406 (1942). Article  ADS  Google Scholar 

* Stéfant, R. J. Alfvén wave damping from finite gyroradius coupling to the ion acoustic mode. _Phys. Fluids_ 13, 440–450 (1970). Article  ADS  Google Scholar  * Lysak, R. L. & Dum, C.

T. Dynamics of magnetosphere-ionosphere coupling including turbulent transport. _J. Geophys. Res._ 88, 365–380 (1983). Article  ADS  Google Scholar  * Kletzing, C. A. Electron acceleration

by kinetic Alfvén waves. _J. Geophys. Res._ 99, 11095–11104 (1994). Article  ADS  Google Scholar  * Kletzing, C. A. & Hu, S. Alfvén wave generated electron time dispersion. _Geophys.

Res. Lett._ 28, 693–696 (2001). Article  ADS  Google Scholar  * Chaston, C. C. ULF Waves and Auroral Electrons. In (eds Takahashi, K., Chi, P. J., Denton, R. E. & Lysak, R. L.)

_Magnetospheric ULF Waves: Synthesis and New Directions_, Vol. 169, 239–257 (American Geophysical Union, 2006). * Howes, G. G. Laboratory space physics: Investigating the physics of space

plasmas in the laboratory. _Phys. Plasmas_ 25, 055501 (2018). Article  ADS  CAS  Google Scholar  * Gekelman, W. et al. The upgraded Large Plasma Device, a machine for studying frontier basic

plasma physics. _Rev. Sci. Instrum._ 87, 025105 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Barenblatt, G. I. _Scaling, Self-similarity, and Intermediate Asymptotics_ (Cambridge

University Press, 1996). * Drake, D. J., Kletzing, C. A., Skiff, F., Howes, G. G. & Vincena, S. Design and use of an Elsässer probe for analysis of Alfvén wave fields according to wave

direction. _Rev. Sci. Instrum._ 82, 103505 (2011). Article  ADS  CAS  PubMed  Google Scholar  * Thuecks, D. J., Skiff, F. & Kletzing, C. A. Measurements of parallel electron velocity

distributions using whistler wave absorption. _Rev. Sci. Instrum._ 83, 083503 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Arunasalam, V., Meservey, E. B., Gurnee, M. N. &

Davidson, R. C. Absorption in a hot plasma near the second harmonic of the electron cyclotron frequency. _Phys. Fluids_ 11, 1076–1084 (1968). Article  ADS  Google Scholar  * Kirkwood, R.,

Hutchinson, I., Luckhardt, S. & Squire, J. Measurement of suprathermal electrons in tokamaks via electron cyclotron transmission. _Nuclear Fusion_ 30, 431 (1990). Article  CAS  Google

Scholar  * Skiff, F., Boyd, D. A. & Colborn, J. A. Measurements of electron parallel-momentum distributions using cyclotron wave transmission*. _Phys. Fluids B_ 5, 2445–2450 (1993).

Article  ADS  CAS  Google Scholar  * Skiff, F., Boyd, D. A. & Colborn, J. A. Measurements of electron dynamics during lower hybrid current drive. _Plasma Phys. Controll. Fusion_ 36,

1371–1379 (1994). Article  ADS  Google Scholar  * Schroeder, J. W. R. et al. Linear theory and measurements of electron oscillations in an inertial Alfvén wave. _Phys. Plasmas_ 24, 032902

(2017). Article  ADS  CAS  Google Scholar  * Schroeder, J. W. R. et al. Direct measurement of electron sloshing of an inertial Alfvén wave. _Geophys. Res. Lett._ 43, 4701–4707 (2016).

Article  ADS  Google Scholar  * Klein, K. G. & Howes, G. G. Measuring collisionless damping in heliospheric plasmas using field-particle correlations. _Astrophys. J. Lett._ 826, L30

(2016). Article  ADS  Google Scholar  * Howes, G. G., Klein, K. G. & Li, T. C. Diagnosing collisionless energy transfer using field-particle correlations: Vlasov-Poisson plasmas. _J.

Plasma Phys._ 83, 705830102 (2017). Article  Google Scholar  * Klein, K. G., Howes, G. G. & TenBarge, J. M. Diagnosing collisionless enegy transfer using field-particle correlations:

gyrokinetic turbulence. _J. Plasma Phys._ 83, 535830401 (2017). Article  Google Scholar  * O’Neil, T. Collisionless damping of nonlinear plasma oscillations. _Phys. Fluids_ 8, 2255–2262

(1965). Article  ADS  MathSciNet  Google Scholar  * Watt, C. E. J. & Rankin, R. Do magnetospheric shear Alfvén waves generate sufficient electron energy flux to power the aurora? _J.

Geophys. Res. Space Phys._ 115, 7224 (2010). Article  ADS  CAS  Google Scholar  * Artemyev, A. V., Rankin, R. & Blanco, M. Electron trapping and acceleration by kinetic Alfvén waves in

the inner magnetosphere. _J. Geophys. Res._ 120, 10,305–10,316 (2015). Google Scholar  * Damiano, P. A., Chaston, C. C., Hull, A. J. & Johnson, J. R. Electron distributions in kinetic

scale field line resonances: a comparison of simulations and observations. _Geophys. Res. Lett._ 45, 5826–5835 (2018). Article  ADS  Google Scholar  * Keiling, A. Alfvén waves and their

roles in the dynamics of the Earth’s magnetotail: a review. _Space Sci. Rev._ 142, 73–156 (2009). Article  ADS  CAS  Google Scholar  * Howes, G. G. et al. Astrophysical gyrokinetics: basic

equations and linear theory. _Astrophys. J._ 651, 590–614 (2006). Article  ADS  Google Scholar  * Klein, K. G. & Howes, G. G. Predicted impacts of proton temperature anisotropy on solar

wind turbulence. _Phys. Plasmas_ 22, 032903 (2015). Article  ADS  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS Supported by DOE grant DE-SC0014599, NSF grants AGS-1054061 and

GRF-1048957, and NASA grant 80NSSC18K1217. The Basic Plasma Science Facility (BAPSF) is supported by grants through the National Science Foundation (PHY-1561912) and the Department of Energy

(DE-FC02-07ER54918). In honor of C. K. Goertz. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Physics, Wheaton College, Wheaton, IL, USA J. W. R. Schroeder * Department of

Physics and Astronomy, University of Iowa, Iowa City, IA, USA G. G. Howes, C. A. Kletzing & F. Skiff * Department of Physics and Astronomy, University of California, Los Angeles, CA, USA

T. A. Carter & S. Vincena * Space Science Institute, Los Angeles, CA, USA S. Dorfman Authors * J. W. R. Schroeder View author publications You can also search for this author inPubMed 

Google Scholar * G. G. Howes View author publications You can also search for this author inPubMed Google Scholar * C. A. Kletzing View author publications You can also search for this

author inPubMed Google Scholar * F. Skiff View author publications You can also search for this author inPubMed Google Scholar * T. A. Carter View author publications You can also search for

this author inPubMed Google Scholar * S. Vincena View author publications You can also search for this author inPubMed Google Scholar * S. Dorfman View author publications You can also

search for this author inPubMed Google Scholar CONTRIBUTIONS J.W.R.S., G.G.H., C.A.K., F.S., T.A.C., S.V., and S.D. designed and performed experiments. J.W.R.S. analyzed experimental data

and, along with F.S., developed the analytical kinetic theory. G.G.H. performed the Liouville mapping and gyrokinetic simulations, and performed the comparison to the auroral acceleration

region. J.W.R.S. and G.G.H. created all figures and wrote the paper together. CORRESPONDING AUTHOR Correspondence to J. W. R. Schroeder. ETHICS DECLARATIONS COMPETING INTERESTS The authors

declare no competing interests. ADDITIONAL INFORMATION PEER REVIEW INFORMATION _Nature Communications_ thanks Robert Lysak, Robert Rankin, Krzysztof Stasiewicz and the other, anonymous,

reviewer for their contribution to the peer review of this work. PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License,

which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link

to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless

indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or

exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints

and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Schroeder, J.W.R., Howes, G.G., Kletzing, C.A. _et al._ Laboratory measurements of the physics of auroral electron acceleration by Alfvén

waves. _Nat Commun_ 12, 3103 (2021). https://doi.org/10.1038/s41467-021-23377-5 Download citation * Received: 13 October 2020 * Accepted: 23 April 2021 * Published: 07 June 2021 * DOI:

https://doi.org/10.1038/s41467-021-23377-5 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative