Large anomalous hall effect in the chiral-lattice antiferromagnet conb3s6

ABSTRACT An ordinary Hall effect in a conductor arises due to the Lorentz force acting on the charge carriers. In ferromagnets, an additional contribution to the Hall effect, the anomalous

Hall effect (AHE), appears proportional to the magnetization. While the AHE is not seen in a collinear antiferromagnet, with zero net magnetization, recently it has been shown that an

intrinsic AHE can be non-zero in non-collinear antiferromagnets as well as in topological materials hosting Weyl nodes near the Fermi energy. Here we report a large anomalous Hall effect

with Hall conductivity of 27 Ω−1 cm−1 in a chiral-lattice antiferromagnet, CoNb3S6 consisting of a small intrinsic ferromagnetic component (≈0.0013 _μ_B per Co) along _c_-axis. This small

moment alone cannot explain the observed size of the AHE. We attribute the AHE to either formation of a complex magnetic texture or the combined effect of the small intrinsic moment on the

electronic band structure. SIMILAR CONTENT BEING VIEWED BY OTHERS _VECTOR-CHIRALITY_ DRIVEN TOPOLOGICAL PHASE TRANSITIONS IN NONCOLLINEAR ANTIFERROMAGNETS AND ITS IMPACT ON ANOMALOUS HALL

EFFECT Article Open access 26 September 2023 FIELD-TUNABLE TOROIDAL MOMENT AND ANOMALOUS HALL EFFECT IN NONCOLLINEAR ANTIFERROMAGNETIC WEYL SEMIMETAL CO1/3TAS2 Article Open access 11 April

2022 HIGH-TEMPERATURE QUANTUM ANOMALOUS HALL REGIME IN A MNBI2TE4/BI2TE3 SUPERLATTICE Article 17 August 2020 INTRODUCTION The anomalous Hall effect (AHE) is a signature of emergent

electromagnetic fields in solids that affect the motion of the electrons, and hence it has been a recent topic of intense study in the context of the topological materials1,2. The Hall

effect in general is an intrinsic property of a conductor due to the Lorentz force experienced by the charge carriers. In systems with spontaneously broken time-reversal symmetry, an

additional contribution, independent of the Lorentz force, is observed, the AHE1. AHE was first observed in ferromagnets where its origin lies in the interplay between spin–orbit coupling

(SOC) and magnetization. Reformulation of the SOC-induced intrinsic mechanism of AHE in ferromagnets to the Berry phase curvature in momentum space has been fruitful in predicting and

describing the AHE in several other systems, including Weyl (semi)metals3, non-collinear antiferromagnets4, non-coplanar magnets5,6,7, and other nontrivial spin textures8,9,10,11. Recent

observations of the large anomalous Hall effect in metals with possible Weyl12,13,14 and massive Dirac fermions15,16 and/or complex spin textures, e.g., skyrmion bubbles17, have generated

interest in such materials, especially for the role of correlated topological states in the emergent electronic properties. Here we present a large AHE in CoNb3S6 that cannot be understood

in terms of conventional mechanisms of the AHE. CoNb3S6 is a member of a large class of intercalated transition metal dichalcogenides, where a 3_d_-transition metal sandwiches between layers

of a 5_d_-transition metal dichalcogenide that are coupled by a weak Van der Waals force. CoNb3S6 represents the 1/3 fractional intercalation of Co atoms between the layers of NbS218. It

crystallizes in the hexagonal chiral space group _P_63 2219,20. It orders antiferromagnetically below ~26 K and is known to have a rather complex susceptibility for the magnetic field

applied parallel to the _c_-axis21,22. At 4 K, neutron diffraction measurement has suggested a collinear antiferromagnetic state in which the spins are in the _ab_-plane pointing along a

certain crystallographic axis20. By itself, however, such a spin structure cannot give rise to the anomalous Hall effect. The key finding of this work is a large _c_-axis anomalous Hall

effect in the antiferromagnetic CoNb3S6. Although CoNb3S6 shows a small, intrinsic ferromagnetic component (≈0.0013 _μ_B per Co) along the _c_-axis, this small moment alone cannot explain

the observed size of the AHE. Based on its chiral crystal structure and the calculated band structure, we attribute the AHE in CoNb3S6 either to the formation of a complex magnetic texture

or to an influence of the small intrinsic ferromagnetic moment on the underlying electronic band structure. RESULTS CRYSTAL STRUCTURE AND PHYSICAL PROPERTIES OF CONB3S6 We verified the room

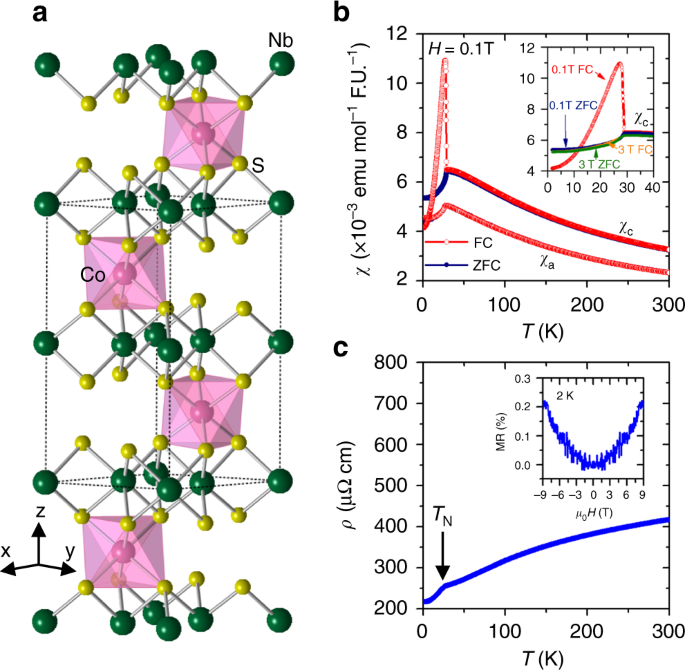
temperature crystal structure of CoNb3S6 in the chiral space group _P_6322 by means of single crystal X-ray diffraction (see Supplementary Note 1 and Supplementary Fig. 1). A sketch of the

crystal structure adopted by CoNb3S6 is shown in Fig. 1a, where the Co atoms occupy the octahedral position between the triangular prismatic layers of the parent compound 2H-NbS2. Figure 1b

shows the magnetic susceptibility of CoNb3S6 as a function of temperature measured with a magnetic field of 0.1 T applied along _a_- and _c_-axis (_χ__a_ and _χ__c_, respectively). Over the

entire temperature range, _χ__c_ exceeds _χ__a_, consistent with behavior reported in the literature21. _χ__a_ shows a kink at _T_N = 27.5 K corresponding to the antiferromagnetic transition

and decreases on further cooling down to 1.8 K. The field cooled (FC) and zero field cooled (ZFC) measurements show identical behavior. Along the _c_-axis, the susceptibility below _T_N

shows irreversibility between FC and ZFC measurements. The ZFC _χ__c_ shows a behavior similar to that of _χ__a_. However, the FC _χ__c_ increases on cooling below _T_N, becomes maximum at

25 K and decreases on further cooling. This increase in FC susceptibility along the _c_-axis near the transition temperature has been reported in previous studies20,21 and implies the

presence of a small ferromagnetic component along the _c_-axis. With increasing magnetic field, the magnitude of this jump decreases, and at 3 T, FC susceptibility shows a continuous

decrease below _T_N, as shown in the inset of Fig. 1b, suggesting that the moment along the _c_-axis is suppressed by a sufficiently large magnetic field. At higher temperatures, the

susceptibility shows Curie–Weiss behavior. A Curie–Weiss fit to the data between 200 and 300 K (Supplementary Note 2 and Supplementary Fig. 2) yields the powder averaged effective moment of

3.0 _μ_B per Co. This value is smaller than the spin-only moment expected for Co2+ (3.87 _μ_B) established by neutron diffraction and optical studies20,23. Resistivity shows metallic

behavior over the measured temperature range of 1.8–300 K, with a sudden drop below 27.5 K (_T_N), presumably due to the reduction of electron scattering with the onset of the spin ordering

(Fig. 1c). CoNb3S6 has a very small magnetoresistance of 0.2% at 2 K in the field of 9 T applied along _c_-axis, as shown in the inset of Fig. 1c. MAGNETIZATION _M_ vs _H_ measured between

29 and 22 K, with the magnetic field along _c_-axis, is shown in Fig. 2a, and the corresponding first-order derivatives are shown in Fig. 2b. Despite the nearly linear _M_–_H_ curves, a

hysteresis with very small remanent magnetization appears below _T_N, which becomes maximum at 25 K (0.0013 _μ_B per formula unit) and decreases at lower temperatures, as shown in Fig. 2b,

c. The hysteresis becomes more clear in d_M_/d_H_ vs _H_ plots shown in Fig. 2b. At 29 K, which is above _T_N, d_M_/d_H_ is featureless. At 27 K, when decreasing the field from 6 T to −6 T,

a peak in d_M_/d_H_ appears at −1 T. When increasing the field from −6 T to 6 T, no peak is seen at −1 T. Instead, the peak is observed at 1 T. These peaks appear at the coercive field of

the hysteresis in _M_ vs _H_. With the decrease in temperature, the coercive field increases and becomes 3 T at 24 K. No such peaks are seen below 24 K. These data suggest that there is an

intrinsic, hard ferromagnetic component along the _c_-axis in the ordered state that is flipped by a temperature-dependent critical field. Switching of this ferromagnetic component gives

rise to the hysteresis in _M_ vs _H_. Below 24 K, a magnetic field of 6 T cannot switch the ferromagnetic component. As a result, no hysteresis is observed. Application of a larger magnetic

field is expected to reveal the hysteresis even below 24 K. In fact, this hysteresis is evident in the Hall effect measurement presented below. In Fig. 2c we show the ferromagnetic component

as a function of the magnetic field obtained by subtracting a linear antiferromagnetic background from the _M_ vs _H_ curves presented in Fig. 2a. On the other hand, when magnetic field is

applied along the _a_-axis, _M_ vs _H_ shows linear behavior at all temperatures measured, as depicted in Fig. 2d–f. HALL EFFECT Hall resistivity (_ρ__yx_) vs _H_ measured between 28 and 23 

K with current along _a_-axis and magnetic field along _c_-axis is depicted in Fig. 3a. The Hall effect at each temperature was measured by cooling the sample in a magnetic field of 9 T and

then by changing the magnetic field from 9 to −9 T and subsequently from −9 to 9 T. At 28 K, which is just above _T_N, the Hall resistivity is linear, as expected for a normal conductor. The

sign of the Hall resistivity indicates that holes are the majority charge carriers in CoNb3S6. Within the single band model, the estimated carrier concentration (_n_ = 1/|_eR_0|) is 2.49 × 

1021 cm−3, where _e_ is the charge of an electron and _R_0 is the ordinary Hall coefficient. When the temperature is lowered below _T_N, an additional contribution appears in the Hall

resistivity. At 27 K, this anomalous Hall signal is small. It increases both in magnitude and in field with decreasing temperature, becoming maximum at 23 K. Below 23 K, no switching

behavior of the Hall resistivity is observed when measured with the maximum field of 9 T. However, the Hall resistivity increases down to 20 K (Supplementary Note 3 and Supplementary Fig. 

3). At 15 K, a very small AHE is observed, and at 2 K there is no anomalous Hall effect. These observations reveal two important points. (1) Hysteresis in the AHE is observed when the

magnetic field switches the small FM component (Fig. 2a–c). (2) The AHE is observed due to the stabilization of the FM component, which is observed between _T_N and 23 K. At 20 K, a magnetic

field of 9 T cannot switch the FM component, and hence the AHE does not switch sign, but gives the same large value. At 2 K, a magnetic field of 9 T cannot induce the FM component at all.

As a result, there is no AHE observed for |_H_| ≤ 9 T. Conventionally, the Hall resistivity in a ferromagnet is given by the relation \(\rho _{yx} = R_0B + \rho

_{{\mathrm{yx}}}^{\mathrm{A}}\), where _R_0 is the ordinary Hall coefficient, \(B = \mu _0H,\,{\mathrm{and}}\,\rho _{{\mathrm{yx}}}^{\mathrm{A}}\) is the anomalous Hall resistivity1. In Fig.

 3a, we see that the Hall resistivity measured in the paramagnetic state, i.e., at 28 K and in the antiferromagnetic state, except near the switching fields has the same slope. This

indicates that _R_0_B_ is constant between 28 and 23 K, and allows us to subtract the ordinary Hall resistivity to obtain the anomalous part. Figure 3b shows \(\rho

_{{\mathrm{yx}}}^{\mathrm{A}}\) vs _H_, where \(\rho _{{\mathrm{yx}}}^{\mathrm{A}}\) is obtained by subtracting the data measured at 28 K from _ρ__yx_ measured below _T_N. As there is a

finite ferromagnetic component along the _c_-axis, we first examine the effect of this small ferromagnetic component on the anomalous Hall effect. For a ferromagnet, \(\rho

_{{\mathrm{yx}}}^{\mathrm{A}} = R_{\mathrm{S}}\mu _0M\), where _R_S is the anomalous Hall coefficient, _μ_0 is the permeability, and _M_ is the magnetization. _R_S scales the _M_–_H_ curve

to the anomalous part of the Hall resistivity. To check for this scaling in CoNb3S6, we obtained the magnetization of the ferromagnetic component by subtracting a straight line from the _M_

vs _H_ curve measured at a representative temperature of 25 K, which shows the maximum remanent magnetization. The obtained magnetization multiplied by −1, (−Δ_M_) vs _H_ is plotted in Fig. 

3c. The anomalous Hall resistivity measured at 25 K is also plotted in the same figure. These plots show that the anomalous Hall effect does scale with magnetization. _R_S is negative and

has an exceedingly large value compared to _R_0. _R_S estimated from this scaling at 25 K is −1.41 × 10−4 m3 C−1, which is four orders of magnitude larger than _R_0 = 2.4 × 10−9 m3 C−1. In a

canonical ferromagnet-like Fe24 or ferromagnets with closely related and even the same crystal structure as CoNb3S6, such as Fe1/4 TaS225 and Fe1/3TaS226, _R_S/R0 ≈ 100, two orders of

magnitude smaller than that in CoNb3S6. This significant boost of the coefficient of AHE in CoNb3S6 is unlikely to be accounted for by the effect of the weak _c_-axis ferromagnetic component

alone and therefore must have an additional contribution. The contribution of the ferromagnetic component to the anomalous Hall resistivity, i.e., _R_S can be estimated from the high

magnetic field part of the anomalous Hall resistivity vs magnetization plot. As \(\rho _{{\mathrm{yx}}}^{\mathrm{A}} = R_{\mathrm{S}}\mu _0M\), the slope of \(\rho

_{{\mathrm{yx}}}^{\mathrm{A}}\) vs _M_ gives _μ_0_R_S. In Fig. 3d, we see that \(\rho _{{\mathrm{yx}}}^{\mathrm{A}}\) vs _M_ resembles \(\rho _{{\mathrm{yx}}}^{\mathrm{A}}\) vs _H_ such that

\(\rho _{{\mathrm{yx}}}^{\mathrm{A}}\) changes sign at the coercive fields. After the abrupt sign change, \(\rho _{{\mathrm{yx}}}^{\mathrm{A}}\) shows a linear variation with _M_. This

linear behavior of \(\rho _{{\mathrm{yx}}}^{\mathrm{A}}\) vs _M_ at high field arises from the continuous spin tilting by the magnetic field toward the _c_-axis and represents the

contribution from the field-induced ferromagnetic component. The slope in this linear regime gives _μ_0_R_S for this compound, which is represented by dashed lines in Fig. 3d. _R_S estimated

from this slope is −1.12 × 10−7 m3 C−1, which is comparable to that of the ferromagnet Fe1/3TaS226. The extra component in the anomalous Hall resistivity, which we label as \(\rho

_{{\mathrm{yx}}}^{{\mathrm{A}}^\prime }\) can be obtained by subtracting this linear part from the anomalous Hall effect: \(\rho _{{\mathrm{yx}}}^{{\mathrm{A}}^\prime } = \rho

_{{\mathrm{yx}}}^{\mathrm{A}} - R_{\mathrm{S}}\mu _0M\) and is shown in Fig. 3e, which shows that contribution from the FM component from spin tilting is negligibly small compared to \(\rho

_{{\mathrm{yx}}}^{\mathrm{A}}\). In Fig. 3f, we plot the anomalous Hall conductivity \(\sigma _{{\mathrm{xy}}}^{\mathrm{A}} = \rho _{{\mathrm{yx}}}^{\mathrm{A}}/\left[ {\left( {\rho

_{{\mathrm{yx}}}^{\mathrm{A}}} \right)^2 + \left( {\rho _{{\mathrm{xx}}}} \right)^2} \right]\) as a function of magnetic field between 27 and 23 K. The anomalous Hall conductivity at 23 K

takes the value 27 Ω−1 cm−1. A similar behavior, in which a very small ferromagnetic component and its anomalously large scaling with the anomalous Hall resistivity, has been observed in

Mn3Sn and Mn3Ge. Here, the anomalous Hall effect has been attributed to the combined effect of non-collinear antiferromagnetic spin texture and electronic band structure12,13. A large

anomalous Hall coefficient, reported for Fe3Sn215,16 cannot be described by the ferromagnetic component alone and is believed to be due to the massive quasi-2D Dirac cones near the Fermi

energy. Likewise, the large AHE observed in frustrated systems such as Pr2Ir2O7 has been attributed to the non-coplanar spin texture27. DISCUSSION We now discuss possible origins of the

anomalous Hall effect in CoNb3S6. First, we can rule out impurity-related extrinsic mechanisms of the AHE from the fact that the AHE vanishes at low temperatures, where the laboratory

magnetic fields are insufficient to alter spins state, e.g., at 2 K as shown in Fig. 3a and Supplementary Fig. 3a. Second, a collinear antiferromagnetic state cannot give rise to the

anomalous Hall effect. Finally, we showed above that an FM component due to simple magnetic field-induced spin tilt alone cannot account for the observed AHE. We thus consider other

scenarios for the origin of the AHE in CoNb3S6: (1) non-collinear, non-coplanar or other complex magnetic textures, or (2) interplay of electronic and magnetic degrees of freedom. CoNb3S6

has a chiral crystal structure. In a magnet with such a chiral lattice, competition among the exchange interaction, Dzyaloshinskii–Moriya interaction (DMI), magnetocrystalline anisotropy,

and Zeeman energy may result in complex magnetic textures28,29,30, including non-collinear or non-coplanar spins that can give rise to large AHE10,11,12,13,27,31. The neutron diffraction

experiment reported by Parkin et al.20 revealed no such complex spin structure. However, this is not unexpected given (1) the measurement is carried out in zero field at 4 K, where our data

does not show AHE when measured up to the magnetic field of 9 T, and (2) a diffraction experiment such as that carried out by Parkin et al. would be insensitive to the large-scale spin

structures. Thus, the nature of the spin structure in CoNb3S6 near _T_N remains an open question. Figure 4a–c shows the paramagnetic band structure of CoNb3S6 without inclusion of SOC. The

metallic character of CoNb3S6 is evident by the presence of the hole pockets along _Γ_−_A_, which is consistent with the measured hole-like character of the charge carriers. There are two

linear electron and hole band crossings along _Γ_−_M_ and _K_−_Γ_. Inclusion of SOC (Fig. 4b) opens a small gap at the band crossings along these lines and splits the bands due to the lack

of inversion symmetry32,33. The band structure along _Γ_−_A_ is enlightening in this regard. In the calculation with SOC (Fig. 4a) both at _Γ_ and _A_, two doubly degenerate bands touch at a

point ≈40 meV above the Fermi energy (_E_F). The splitting of these bands due to SOC along _Γ_−_A_ (Fig. 4b) is remarkably large and results in the formation of several linearly crossing

bands and avoided crossings. In Fig. 4d, we show the band dispersion along _A_–_Γ_–_A_ near _E_F (see Supplementary Note 4 and Supplementary Fig. 4 for symmetry analysis). Bands cross

linearly at all of these points. Two of these points lie within ≈15 meV of _E_F. It has been established rigorously that in non-magnetic crystals and in directions parallel to a 63 screw

axis (along _Γ_−_A_ in CoNb3S6), band degeneracies at the _Γ_ points are Weyl nodes34. The AHE in CoNb3S6 is observed only when the external magnetic field induces a small moment along

_c_-axis, which suggests that the large enhancement in AHE may result due to the combined effect of such a field in the presence of the near _E_F Weyl nodes. In summary, CoNb3S6 is a member

of the class of antiferromagnets that show a large anomalous Hall effect. The large AHE is not explained by the reported collinear antiferromagnetic structure, and we suggest the formation

of complex, noncollinear magnetic textures or an interplay between the magnetic texture and electronic band structure as two possible mechanisms for the large AHE. CoNb3S6 is a member of a

large family of the 1/3 intercalated TX2 compounds, where T is a 4- or 5-_d_ transition metal element, and X is a chalcogen (S, Se). As the change in the intercalated 3_d_ element changes

the nature of both magnetic and electronic structure, our realization of the AHE in CoNb3S6 opens a platform to explore and perhaps manipulate the interplay among spin texture, electronic

band structure, and the associated emergent phenomena in a large class of poorly explored materials. METHODS CRYSTAL GROWTH AND CHARACTERIZATION Single crystals of CoNb3S6 were grown by

chemical vapor transport using iodine as the transport agent. First, a polycrystalline sample was prepared by heating stoichiometric amounts of cobalt powder (Alfa Aesar 99.998%), niobium

powder (Johnson Matthey Electronics 99.8%), and sulfur pieces (Alfa Aesar 99.9995%) in an evacuated silica ampoule at 900 °C for 5 days. Subsequently, 2 g of the powder was loaded together

with 0.5 g of iodine in a fused silica tube of 14 mm inner diameter. The tube was evacuated and sealed under vacuum. The ampoule of 11 cm length was loaded in a horizontal tube furnace in

which the temperature of the hot zone was kept at 950 °C and that of the cold zone was ≈850 °C for 7 days. Several CoNb3S6 crystals formed with a distinct, well-faceted flat plate-like

morphology. The crystals of CoNb3S6 were examined by single crystal X-ray diffraction at beamline 15-ID-D at the APS, Argonne National Laboratory (ANL), where the data were collected with an

APEX2 Area Detector using synchrotron radiation (_λ_ = 0.41328 Å) at 293 K. Compositional analysis was done using an energy dispersive X-ray spectroscopy (EDS) at the Electron Microscopy

Center, ANL. MAGNETIC AND TRANSPORT PROPERTY MEASUREMENTS Magnetization measurements were made using a Quantum Design VSM SQUID. Both in FC and ZFC mode, susceptibility data were measured by

sweeping temperature up from 1.8 K. In the derivative of _M_ vs _H_, we observed a small peak around _H_ = 0 both above and below _T_N and both along _a_- and _c_-axis, possibly due to an

unknown paramagnetic impurity. For data at all temperatures presented in Fig. 2, a background measured at 30 K was subtracted. A small asymmetry of the peak position in the d_M_/d_H_ vs _H_

was observed when only one loop of _M_ vs _H_ was measured. We did not see such an asymmetry when a second loop of the _M_ vs _H_ was measured, which is presented in Fig. 2. Transport

measurements were performed on a quantum design PPMS following a conventional 4-probe method. Au wires of 25 μm diameter were attached to the sample with Epotek H20E silver epoxy. An

electric current of 1 mA was used for the transport measurements. In magnetoresistance measurements, the contact misalignment was corrected by field symmetrizing the measured data. The

following method was adopted for the contact misalignment correction in Hall effect measurements. The Hall resistance was measured at _H_ = 0 by decreasing the field from the positive

magnetic field (_R__H_+), where _H_ represents the external magnetic field. Again the Hall resistance was measured at _H_ = 0 by increasing the field from negative magnetic field (_R__H_−).

Average of the absolute value of (_R__H_+) and (_R__H_−) was then subtracted from the measured Hall resistance. The conventional antisymmetrization method was also used for the Hall

resistance measured at 28 K (above _T_N) and at 2 K (where no anomalous Hall effect was observed), which gave same result as obtained from the former method. ELECTRONIC STRUCTURE

CALCULATIONS The electronic structure calculations were carried out within density functional theory (DFT) using the all-electron, full potential code WIEN2K35 based on the augmented plane

wave plus local orbital (APW + lo) basis set36. The Perdew–Burke–Ernzerhof (PBE) version of the generalized gradient approximation (GGA)37 was chosen as the exchange correlation potential.

Spin–orbit coupling (SOC) was introduced in a second variational procedure38. A dense _k_-mesh of 28 × 28 × 12 was used for the Brillouin zone (BZ) sampling. A _R_MT_K_max of 7.0 was chosen

for all calculations. Muffin tin radii were 2.5 a.u. for Nb, 2.45 a.u. for Co, and 2.01 a.u. for S. DATA AVAILABILITY The authors declare that the main data supporting the findings of this

study are available within the article and its Supplementary Information files. Extra data are available from the corresponding author on request. REFERENCES * Nagaosa, N., Sinova, J.,

Onoda, S., McDonald, A. H. & Ong, N. P. Anomalous Hall effect. _Rev. Mod. Phys._ 82, 1539–1592 (2010). Article  ADS  Google Scholar  * Nagaosa, N., Yu, X. Z. & Tokura, Y. Gauge

fields in real and momentum spaces in magnets: monopoles and skyrmions. _Philos. Trans. R. Soc. A_ 370, 5806–5819 (2012). Article  ADS  CAS  Google Scholar  * Burkov, A. A. Anomalous Hall

effect in Weyl metals. _Phys. Rev. Lett._ 113, 187202 (2014). Article  ADS  PubMed  CAS  Google Scholar  * Chen, H., Niu, Q. & MacDonald, A. H. Anomalous Hall effect arising from

noncollinear antiferromagnetism. _Phys. Rev. Lett._ 112, 017205 (2014). Article  ADS  PubMed  CAS  Google Scholar  * Shindou, R. & Nagaosa, N. Orbital ferromagnetism and anomalous Hall

effect in antiferromagnets on the distorted fcc lattice. _Phys. Rev. Lett._ 87, 116801 (2001). Article  ADS  PubMed  CAS  Google Scholar  * Ohgushi, K., Murakami, S. & Nagaosa, N. Spin

anisotropy and quantum Hall effect in the kagome lattice: chiral spin state based on a ferromagnet. _Phys. Rev. B_ 62, R6065 (2000). Article  ADS  CAS  Google Scholar  * Martin, I. &

Batista, C. D. Itinerant electron-driven chiral magnetic ordering and spontaneous quantum Hall effect in triangular lattice models. _Phys. Rev. Lett._ 101, 156402 (2008). Article  ADS 

PubMed  CAS  Google Scholar  * Schulz, T. et al. Emergent electrodynamics of skyrmions in a chiral magnet. _Nat. Phys._ 8, 301–304 (2012). Article  CAS  Google Scholar  * Nagaosa, N. &

Tokura, Y. Topological properties and dynamics of magnetic skyrmions. _Nat. Nanotechnol._ 8, 899–911 (2013). Article  ADS  PubMed  CAS  Google Scholar  * Neubauer, A. et al. Topological Hall

effect in the _A_ phase of MnSi. _Phys. Rev. Lett._ 102, 186602 (2009). Article  ADS  PubMed  CAS  Google Scholar  * Kanazawa, N. et al. Large topological Hall effect in a short-period

helimagnet MnGe. _Phys. Rev. Lett._ 106, 156603 (2011). Article  ADS  PubMed  CAS  Google Scholar  * Nakatsuji, S., Kiyohara, N. & Higo, T. Large anomalous Hall effect in a non-collinear

antiferromagnet at room temperature. _Nature_ 527, 212–215 (2015). Article  ADS  PubMed  CAS  Google Scholar  * Nayak, A. K. et al. Large anomalous Hall effect driven by a nonvanishing

Berry curvature in the noncolinear antiferromagnet Mn3Ge. _Sci. Adv._ 2, e1501870 (2016). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Kuroda, K. et al. Evidence for magnetic

Weyl fermions in a correlated metal. _Nat. Mater._ 16, 1090–1095 (2017). Article  ADS  PubMed  CAS  Google Scholar  * Kida, T. et al. The giant anomalous Hall effect in the ferromagnet

Fe3Sn2−a frustrated kagome metal. _J. Phys.: Condens. Matter_ 23, 112205 (2011). ADS  CAS  Google Scholar  * Ye, L. et al. Massive dirac fermions in a ferromagnetic kagome metal. _Nature_

555, 638–642 (2018). Article  ADS  PubMed  CAS  Google Scholar  * Hou, Z. et al. Observation of various and spontaneous magnetic skyrmionic bubbles at room temperature in a frustrated kagome

magnet with uniaxial magnetic anisotropy. _Adv. Mater._ 29, 1701144 (2017). Article  CAS  Google Scholar  * Beal, A. R. in _Intercalated Layered Materials_ Vol. 6 (ed. Lévy, F.) 251–305 (D.

Reidel Publishing Company, Dordrecht, 1979). * Anzenhofer, K., van den Berg, J. M., Cossee, P. & Helle, J. N. The crystal structure and magnetic susceptibilities of MnNb3S6, FeNb3S6,

CoNb3S6 and NiNb3S6. _J. Phys. Chem. Solids_ 31, 1057–1067 (1970). Article  ADS  CAS  Google Scholar  * Parkin, S. S. P., Marseglia, E. A. & Brown, P. J. Magnetic structure of Co1/3NbS2

and Co1/3TaS2. _J. Phys. C: Solid State Phys._ 16, 2765–2778 (1983). Article  ADS  CAS  Google Scholar  * Friend, R. H., Beal, A. R. & Yoffe, A. D. Electrical and magnetic properties of

some first row transition metal intercalates of niobium disulphide. _Philos. Mag._ 35, 1269–1287 (1977). Article  ADS  CAS  Google Scholar  * Barišić, N. et al. High-pressure study of

transport properties in Co0.33NbS2. _Phys. Rev. B_ 84, 075157 (2011). Article  ADS  CAS  Google Scholar  * Beal, A. R. & Liang, W. Y. Reflectivity spectra of some first row transition

metal intercalates of NbS2. _Philos. Mag._ 33, 121–131 (1976). Article  ADS  CAS  Google Scholar  * Dheer, P. N. Galvanomagnetic effects in iron whiskers*. _Phys. Rev._ 156, 637–644 (1967).

Article  ADS  CAS  Google Scholar  * Checkelsky, J. G., Lee, M., Morosan, E., Cava, R. J. & Ong, N. P. Anomalous Hall effect and magnetoresistance in the layered ferromagnet Fe1/4TaS2:

The inelastic regime. _Phys. Rev. B_ 77, 014433 (2008). Article  ADS  CAS  Google Scholar  * Dijkstra, J., Zijlema, P. J., van Bruggen, C. F., Haas, C. & de Groot, R. A. Band-structure

calculations of Fe1/3TaS2 and Mn1/3TaS2, and transport and magnetic properties of Fe0.28TaS2. _J. Phys.: Condens. Matter_ 1, 6363–6379 (1989). Article  ADS  CAS  Google Scholar  * Machida,

Y. et al. Unconventional anomalous Hall effect enhanced by a noncoplanar spin texture in the frustrated kondo lattice Pr2Ir2O7. _Phys. Rev. Lett._ 98, 057203 (2007). Article  ADS  PubMed 

CAS  Google Scholar  * Rößler, U. K., Leonov, A. A. & Bogdanov, A. N. Chiral Skyrmionic matter in non-centrosymmetric magnets. _J. Phys.: Conf. Ser._ 303, 012105 (2011). Google Scholar 

* Bogdanov, A. N., Rößler, U. K., Wolf, M. & Müller, K.-H. Magnetic structures and reorientation transitions in noncentrosymmetric uniaxial antiferromagnets. _Phys. Rev. B_ 66, 214410

(2002). Article  ADS  CAS  Google Scholar  * Bogdanov, A. N. & Yablonskiĭ, D. A. Contribution to the theory of inhomogeneous states of magnets in the region of magnetic-field-induced

phase transitions. Mixed state of antiferromagnets. _Sov. Phys. JETP_ 69, 142 (1989). Google Scholar  * Sürgers, C., Fischer, G., Winkel, P. & Löhneysen, H. v. Large topological Hall

effect in the non-collinear phase of an antiferromagnet. _Nat. Commun._ 5, 3400 (2014). Article  PubMed  ADS  CAS  Google Scholar  * Winker, R. _Spin–Orbit Coupling Effects in

Two-dimensional Electron and Hole Systems_ (Springer-Verlag, Berlin Heidelberg, 2003). * Silsbee, R. H. Spin–orbit induced coupling of charge current and spin polarization. _J. Phys.:

Condens. Matter_ 16, R179–R207 (2004). ADS  CAS  Google Scholar  * Tsirkin, S. S., Souza, I. & Vanderbilt, D. Composite Weyl nodes stabilized by screw symmetry with and without

time-reversal invariance. _Phys. Rev. B_ 96, 045102 (2017). Article  ADS  Google Scholar  * Blaha, P. et al. _WIEN2K, An Augmented Plane Wave Plus Local Orbitals Program for Calculating

Crystal Properties_ (Vienna University of Technology, Austria, 2001). Google Scholar  * Sjöstedt, E., Nordström, L. & Singh, D. J. An alternative way of linearizing the augmented

plane-wave method. _Solid State Commun._ 114, 15–20 (2000). Article  ADS  Google Scholar  * Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple.

_Phys. Rev. Lett._ 77, 3865 (1996). Article  ADS  PubMed  CAS  Google Scholar  * Singh, D. J. & Nordström, L. _Plane Waves, Pseudopotentials and LAPW Method_ (Springer, New York, 2006).

Download references ACKNOWLEDGEMENTS This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Science and Engineering Division. The

authors thank insightful discussion with Daniel Phelan, I. Martin, F. Wu, Y. Xu, X. Dai, S. Chen and Z.-X. Shen. The EDS measurements were performed at the Center for Nanoscale materials in

the Electron Microscopy Center, which was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357. ChemMatCARS

Sector 15 is principally supported by the Divisions of Chemistry (CHE) and Materials Research (DMR), National Science Foundation, under Grant NSF/CHE-1346572. Use of the Advanced Photon

Source, an Office of Science User Facility operated for the US Department of Energy (DOE) Office of Science by Argonne National Laboratory, was supported by the US DOE under Contract

DE-AC02-06CH11357. We acknowledge the computing resources provided on Blues, a high-performance computing cluster operated by Argonne’s Laboratory Computing Resource Center. AUTHOR

INFORMATION AUTHORS AND AFFILIATIONS * Materials Science Division, Argonne National Laboratory, 9700 South Cass Avenue, Argonne, IL, 60439, USA Nirmal J. Ghimire, A. S. Botana, J. S. Jiang, 

Junjie Zhang & J. F. Mitchell * ChemMatCARS, The University of Chicago, Argonne, IL, 60439, USA Y.-S. Chen Authors * Nirmal J. Ghimire View author publications You can also search for

this author inPubMed Google Scholar * A. S. Botana View author publications You can also search for this author inPubMed Google Scholar * J. S. Jiang View author publications You can also

search for this author inPubMed Google Scholar * Junjie Zhang View author publications You can also search for this author inPubMed Google Scholar * Y.-S. Chen View author publications You

can also search for this author inPubMed Google Scholar * J. F. Mitchell View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS N.J.G. and J.F.M.

conceived the project. N.J.G. grew the crystals, performed the magnetic and magnetotransport measurements. J.S.J. contributed to the transport measurements. A.B. calculated the electronic

band structure. Y.S.C. and J.Z. did the single crystal X-ray diffraction experiments. N.J.G. and J.F.M. wrote the manuscript. All authors contributed to the discussion of the results.

CORRESPONDING AUTHOR Correspondence to Nirmal J. Ghimire. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE:

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. ELECTRONIC SUPPLEMENTARY MATERIAL SUPPLEMENTARY INFORMATION RIGHTS AND

PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any

medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The

images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not

included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly

from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Ghimire, N.J.,

Botana, A.S., Jiang, J.S. _et al._ Large anomalous Hall effect in the chiral-lattice antiferromagnet CoNb3S6. _Nat Commun_ 9, 3280 (2018). https://doi.org/10.1038/s41467-018-05756-7 Download

citation * Received: 12 March 2018 * Accepted: 02 July 2018 * Published: 16 August 2018 * DOI: https://doi.org/10.1038/s41467-018-05756-7 SHARE THIS ARTICLE Anyone you share the following

link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature

SharedIt content-sharing initiative