Cooperative polariton dynamics in feedback-coupled cavities

ABSTRACT The emerging field of cavity spintronics utilizes the cavity magnon polariton (CMP) induced by magnon Rabi oscillations. In contrast to a single-spin quantum system, such a

cooperative spin dynamics in the linear regime is governed by the classical physics of harmonic oscillators. It makes the magnon Rabi frequency independent of the photon Fock state

occupation, and thereby restricts the quantum application of CMP. Here we show that a feedback cavity architecture breaks the harmonic-oscillator restriction. By increasing the feedback

photon number, we observe an increase in the Rabi frequency, accompanied with the evolution of CMP to a cavity magnon triplet and a cavity magnon quintuplet. We present a theory that

explains these features. Our results reveal the physics of cooperative polariton dynamics in feedback-coupled cavities, and open up new avenues for exploiting the light–matter interactions.

SIMILAR CONTENT BEING VIEWED BY OTHERS THE ROLE OF EXCITATION VECTOR FIELDS AND ALL-POLARISATION STATE CONTROL IN CAVITY MAGNONICS Article Open access 04 December 2024 INTERCAVITY POLARITON

SLOWS DOWN DYNAMICS IN STRONGLY COUPLED CAVITIES Article Open access 04 April 2024 SPIN-CORRELATED EXCITON–POLARITONS IN A VAN DER WAALS MAGNET Article 12 September 2022 INTRODUCTION

Controlling cooperativity is essential for utilizing the light–matter interactions1. For light coupled with quantum systems, cooperativity measures the ratio of Rabi frequency to decay rates

and can be controlled by changing the photon Fock state occupation2. Recently, high cooperativity was demonstrated in hybridizing magnons and cavity microwave photons3,4,5,6,7,8,9,10. In

contrast to a single spin system2, the harmonic oscillator nature of the ensemble of spins in the linear dynamic regime makes the magnon Rabi frequency independent of the photon

number11,12,13,14. Breaking the harmonic limit has been a pursuit of continuing interest in the study of collective dynamics, as, for example, in the case of the Kohn theorem15,16,17. The

same quest is developing in the new field of cavity spintronics18, where it is required for quantum control of collective spin dynamics19, 20. Here we show that a feedback cavity

architecture breaks the harmonic limit for magnon–photon coupling. By increasing the voltage-controlled feedback photon number, we observe an increase of the Rabi frequency, accompanied with

the evolution of the cavity magnon polariton7, 11, 12 to a cavity magnon triplet and a cavity magnon quintuplet. The unprecedented capability of on-chip control of magnon-photon

cooperativity, which our theory links to the physics of cooperative polariton dynamics, may open up exciting opportunities for exploiting the light–matter interactions. RESULTS DEVICE

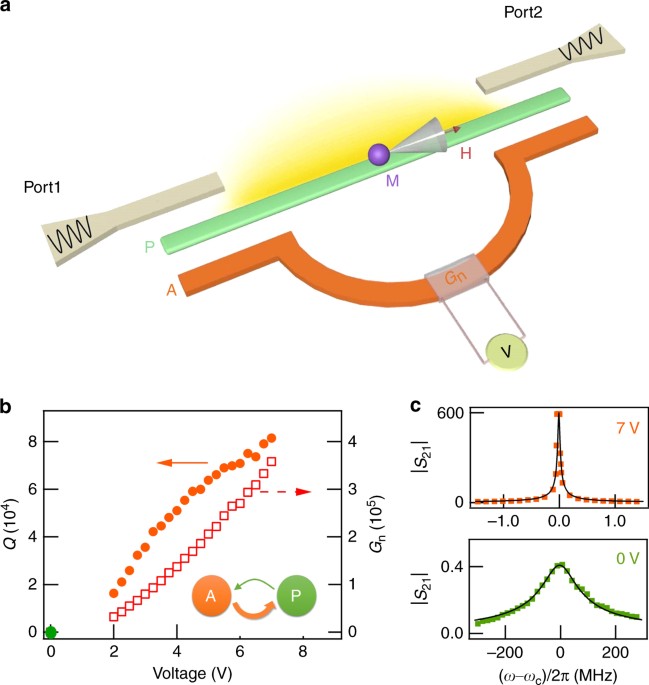
ARCHITECTURE Our experimental setup is schematically shown in Fig. 1a. We use a planar passive cavity (P) with a mode frequency _ω_ _c_ to couple photons with the magnons (M) in a

ferromagnetic insulator yttrium iron garnet (YIG). The YIG sphere is placed on top of the cavity at an adjustable distance _d_. An external magnetic field H is applied parallel to the cavity

to tune the magnon frequency _ω_ _r_ . When _ω_ _r_ approaches _ω_ _c_ , the magnon–photon coupling21 produces the cavity magnon polariton (CMP)7 in the P–M device, which is detected by

using a two-port vector network analyzer (VNA) that measures the transmission coefficient _S_ 21(_ω_) of the P-cavity. The key innovation of our experiment, in comparison with the recent

pioneering studies of magnon–photon coupling3,4,5,6,7,8,9,10, is the design and implementation of an active cavity (A), which contains a microwave amplifier with voltage (V)-controlled gain

(_G_ _n_ ). The two cavities (A and P) are carefully designed to have the same mode frequency. They are weakly coupled and phase matched to each other (see Supplementary Notes 1–3 for

details). Such a feedback-coupled cavity architecture is crucial as it offers more capabilities than the versatile double beam technique22: Essentially, the A-cavity acts as a feedback loop

to compensate the microwave loss of the P-cavity, and produces a gain up to 360,000; the cavity quality factor is tunable up to 81,500, about three orders of magnitude higher than

conventional planar cavities. Furthermore, feedback photons couple with the CMP, and thus coherently enhance the strong coupling in the P-M device. Altogether, these capabilities reveal a

hidden cooperative effect of polariton dynamics, which has escaped studies ever since 1954, when Dicke elucidated the cooperative molecular dynamics23 that led to the development of

super-radiant devices24, 25. A dozen A-P-M devices with different geometries were designed and showed consistent results, with a variety of new effects involving the light–matter

interactions being revealed. In this paper the emphasis is on data rendered from a typical device, which focuses on the fundamental issue of the breaking of the harmonic protection of

magnon-photon cooperativity. The magnon mode we study has Gilbert damping parameter _α_ = 2.0 × 10−4, and the dispersion follows the Kittel formula \(\omega _r = \gamma \mu _0\left( {\left|

H \right| + H_A} \right)\). Here, _γ_ = 173 GHz T−1 is the electron gyromagnetic ratio, _μ_ 0 _H_ _A_  = 8.56 mT is the effective field3,4,5,6,7,8,9,10, and _μ_ 0 is the permeability of

vacuum. We study the A-P-M devices by using three methods to systematically control the CMP: (i) tuning _d_ to control the P-M coupling strength, (ii) tuning _V_ to control the feedback

photon number, and (iii) tuning _H_ to change the frequency detuning \(\Delta \equiv \omega _r - \omega _c\). DISTANCE _D_ DEPENDENT RABI FREQUENCY We begin our study with the feedback

switched off (_V_ = 0) and with an intra-cavity photon number of about 106. Figure 2a shows the |_S_ 21| spectra measured at zero detuning (Δ = 0). Within the broad cavity mode of _Q_ = 25,

a dip appears at _ω_ _c_ /2_π_ = 3.160 GHz. This is the characteristic spectral response of CMP in the regime of magnetically induced transparency5 defined by \(1/2 Q >\Omega_0 / \omega_c

>\alpha\). The Rabi frequency _Ω_ 0 depends on _d_ since the rf field of the P-cavity increases with decreasing _d_. By fitting the |_S_ 21| spectra using the CMP theory5, 11, 12, we

deduce _Ω_ 0 and plot the _Ω_ 0−_d_ dependence in Fig. 2b (the solid circles). The expected value of _Ω_ 0 is given by3,4,5, 12, 21 $$\Omega _0 = g_0\sqrt N ,$$ (1) where \(g_0 = \eta \gamma

\sqrt {5\mu _0\hbar \omega _c/4V_c}\) is the vacuum Rabi frequency of a single spin, _N_ = 1.1 × 1019 is the total number of spins in the YIG sphere, and _V_ _c_ is the cavity mode volume.

\(\eta = h\left( d \right)/h\left( 0 \right)\) describes _d_-dependent spatial overlap between the rf field _h_ and the magnon mode in YIG5, which we calculate by using a Maxwell’s equations

solver. With _V_ _c_  = 7.98 × 10−5 m3 as the only fitting parameter, the calculated Rabi frequency is plotted in Fig. 2b (solid curve), and agrees well with the measured result. Eq. (1)

shows that _Ω_ 0 has an \(\sqrt N\)-fold enhancement from _g_ 0. It is this cooperative spin dynamic effect14, 21, 23, 26 that makes cavity magnon systems highly interesting3,4,5,6,7,8,9,10.

However, such a collective dynamics has a drawback: a single quantum two-level system can be saturated by one photon excitation, so that adding photons enhances the Rabi frequency2, but the

magnon-photon coupling exhibits classical behavior7 of coupled harmonic oscillators11, 12. In the linear dynamic regime where the number of CMP \(m \ll N\), the spin ensemble is far from

being saturated, so that adding photons may increase _m_ but does not change _Ω_ 0. Hence, in contrast to quantum systems2, the magnon-photon cooperativity, \(C \equiv 2(\Omega _0/\omega

_c)^2Q/\alpha\), has been found to be independent of photon number7. Breaking such a harmonic limit without interfering with the complex nonlinear magnetization dynamics21, 27, 28 seems

impossible. But, as we reveal below, a distinct cooperative polariton dynamics may be used in the linear dynamic regime (\(m \ll N\)), which enables tuning of the magnon Rabi frequency by

the changing of the feedback photon numbers. FEEDBACK DEPENDENT RABI FREQUENCY Figure 2c shows the |_S_ 21| spectra still measured at Δ = 0, but with the amplifier switched on at _V_ = 7 V.

Feedback gain of _G_ _n_  = 3.6 × 105 with a feedback photon number of _n_ = 1 × 1013 is created. The cavity mode frequency shifts slightly to _ω_ _c_ /2_π_ = 3.177 GHz, while the _Q_-factor

is significantly increased to 81,500. Noticeably, the A-P-M device enters the strong coupling regime3,4,5,6,7,8,9,10, where \(\Omega_f / \omega_c >\alpha >1/2 Q\). Here, _Ω_ _f_ is

the Rabi frequency enhanced by the feedback photons, and is deduced from the two side peaks at _ω_ _c_ ±_Ω_ _f_ . As shown in Fig. 2b, both _Ω_ _f_ and _Ω_ 0 increase with decreasing _d_,

but the ratio of _Ω_ _f_ /_Ω_ 0 = 1.5 stays constant. Another remarkable feature is that a sharp resonance appears in the spectral center at _ω_ _c_ , indicating that the twin CMP evolve to

a cavity magnon triplet. It resembles the Mollow triplet29, a canonical signature of the light–matter interaction observed in single quantum systems22. The characteristic trait of the Mollow

triplet is that the Rabi splitting increases with the photon number22, 29. This is verified in Fig. 3a where we plot the |_S_ 21| spectra measured by changing _V_, while keeping the A-P-M

device at Δ = 0 with fixed _d_ = 0.58 mm (corresponding to _Ω_ 0/2_π_ = 7.5 MHz). As the feedback photon number is increased by increasing _G_ _n_ , the Rabi splitting increases as shown in

Fig. 3b. We find that, numerically, the measured Rabi splitting scales with _G_ _n_ via a simple relation of \(\Omega_f/ \Omega_0 = \left( {1 + \xi \sqrt {G_n} } \right)^{1/2}\) with _ξ_ = 

2.7 ×10−3. We also find that the scaling parameter _ξ_ differs from device to device. COOPERATIVE POLARITON DYNAMICS Now, we quantitatively explain all these results through a model which we

develop to unveil the underlying physics of cooperative polariton dynamics. Without feedback coupling, the Hamiltonian describing _N_ spins collectively coupled with a cavity mode is26

\(\hat H_0/\hbar = \omega_c\hat p^\dagger \hat p + \omega_r\hat S^z + g_0\left( {\hat S^ + \hat p + \hat p^\dagger \hat S^ - } \right)\). Here, the creation (annihilation) operators \(\hat

p^\dagger \left( {\hat p} \right)\) describe the P-cavity mode, \(\vec S = \mathop {\sum}\nolimits_{j = 1}^N \vec S_j\) is the collective spin (magnon) variable, with each spin in YIG

characterized by the operators \(\hat S_j^ \pm = \hat S_j^x \pm i\hat S_j^y\) and \(\hat S_j^z\). Denoting \(\left| {(S,M)} \right\rangle\) as the eigenstate of \(\hat S^2\) and \(\hat

S^z\), and \(\left| 0 \right\rangle\) as the vacuum of the radiation field, the ground state of the coupled spin-photon system21 is \(\left| {G;0} \right\rangle = \left| {\left( {N/2, - N/2}

\right);0} \right\rangle\). The excited states, denoted by \(\left| {G;1} \right\rangle = \left| {\left( {N/2, - N/2} \right);1} \right\rangle\) and \(\left| {E;0} \right\rangle = \left|

{\left( {N/2, - N/2 + 1} \right);0} \right\rangle\), respectively, are coupled to produce two CMP states \(\left| \pm \right\rangle = c_ \pm \left| {E;0} \right\rangle \pm c_ \mp \left|

{G;1} \right\rangle\), where \(c_ \pm = \sqrt {\left( {\Omega \pm \Delta /2} \right)/2\Omega }\) are the state amplitudes with \(\Omega \equiv \sqrt {\Omega_0^2 + \left( {\Delta /2}

\right)^2}\). In the CMP basis, collective excitations from \(\left| {G;0} \right\rangle\) to \(\left| \pm \right\rangle\) lead to the twin CMP modes appearing at \(\omega _ \pm = \omega _c

+ \Delta /2 \pm \Omega\). With feedback coupling, all _m_ CMPs produced by magnon-photon coupling are interacting collectively with _n_ feedback photons. We find that such a cooperative

polariton dynamics is described by the Hamiltonian (see Supplementary Notes 4–6 for details) $$\hat H/\hbar = \omega _c\hat a^\dagger \hat a + \mathop {\sum}\limits_{k = \pm } \omega _k\hat

m_k^z + \mathop {\sum}\limits_{k = \pm } \frac{{c_k\Omega _0}}{{\sqrt m }}\left( {\hat m_k^ + \hat a + \hat a^\dagger \hat m_k^ - } \right),$$ (2) where \(\hat a^\dagger \left( {\hat a}

\right)\) describe the feedback photons, \(\hat m_ \pm ^z = \left| \pm \right\rangle \left\langle \pm \right|\), \(\hat m_ \pm ^ + = \left| \pm \right\rangle \left\langle {G;0} \right|\),

and \(\hat m_ \pm ^ - = \left| {G;0} \right\rangle \left\langle \pm \right|\) are two-level operators written in the CMP basis. Eq. (2) links two coherent cooperative dynamics: the

collective excitation of the _N_ spin ensemble by magnon-photon coupling, and the collective de-excitation of the _m_ CMP ensemble due to the coupling of polaritons with the coherently

fedback photons. It leads to dressed states2, as shown in Fig. 3c. The feedback enhanced Rabi frequency is calculated (see Supplementary Note 6) for each CMP mode by considering the coupling

between the states \(\left| \pm \right\rangle \left| n \right\rangle\) and \(\left| {G;0} \right\rangle \left| {n + 1} \right\rangle\), and we find $$\Omega _ \pm = \sqrt {\left( {\Omega

\pm \Delta /2} \right)^2 + 2\left( {f\Omega _0} \right)^2\left( {\Omega \pm \Delta /2} \right)/\Omega } ,$$ (3) where \(f \equiv \sqrt {n/m}\) is the feedback factor that can be tuned by

changing _G_ _n_ . At Δ = 0, we obtain from Eq. (3) \(\Omega _ \pm = \Omega _f = \Omega _0\sqrt {1 + 2f^2}\), which means that the two sets of dressed states shown in Fig. 3c have the same

Rabi splitting. Therefore, they produce the same triplet at _ω_ _c_ and _ω_ _c_ ±_Ω_ _f_ , as observed in Figs. 2c and 3a. Setting _f_ = 0.78 for _V_ = 7 V, we obtain _Ω_ _f_  = 1.5_Ω_ 0,

which produces the dashed line in Fig. 2b. When the gain is tuned by changing V, we have \(n \propto G_n\). In the linear regime, by assuming that the number of CMP is proportional to the

non-equilibrium magnetization which depends linearly on the rf field _h_ 27, we find \(m \propto \sqrt {G_n}\). Hence, Eq. (3) leads to the scaling of \(\Omega _f / \Omega _0 = \left( {1 +

\xi \sqrt {G_n} } \right)^{1/2}\) at Δ = 0, where ξ is a device-specific parameter. This gives the theoretical curve calculated in Fig. 3b. Furthermore, Eq. (3) predicts that at \(\Delta

\ne\)0, a cavity magnon triplet will split because \(\Omega _ + \ne \Omega _ -\). Five modes are expected to appear at _ω_ _c_ , _ω_ _c_ ±_Ω_ +, and _ω_ _c_ ±_Ω_ −. Indeed, such an

intriguing cavity magnon quintuplet, produced by the cooperative dynamics of CMP, occurs when we change the _H_ field. CAVITY MAGNON QUINTUPLET Figure 4a shows the |_S_ 21| spectra measured

at different _H_, with fixed _V_ = 7 V and _d_ = 0.6 mm. Clearly, when Δ is tuned away from zero, each of the modes at \(\omega _ \pm / 2\pi = 3.177 \pm \Omega _f / 2\pi\) split into a

doublet, and the splitting increases with |Δ|. The quintuplet dispersions are plotted in Fig. 4b, 4c as a function of _H_ and Δ, respectively. Using _f_ = 0.78 and _Ω_ 0/2_π_ = 7.2 MHz

determined from Fig. 2, we calculate the dispersions from Eq. (3) without any other parameters. The result agrees very well with the measured data, as shown in Fig. 4c. Thus, the A-P-M

devices coherently utilize two correlated aspects of cooperative dynamics in the feedback-coupled cavity systems. The first aspect, known for more than six decades as cooperative spin

dynamics, is rooted in Dicke’s seminal work23. Signified by the Dicke factor \(\sqrt N\), it describes the collective dynamics of the _N_ spin system coupled with the vacuum of the radiation

field. The second aspect, revealed in this work as cooperative polariton dynamics, shows the collective dynamics of _m_ polaritons coupled with the higher Fock states of _n_ feedback

photons, which manifests itself by the feedback factor of \(\sqrt {n/m}\). Using this effect, we demonstrate the breaking of harmonic protection for magnon-photon cooperativity in the linear

dynamic regime (\(m \ll N\)), and discover the evolution of CMP to a cavity magnon triplet and a quintuplet. We note that although our experiment is based on a ferromagnetic YIG sample, the

physics of cooperative polariton dynamics revealed in our study is general. With the feedback cavity technique, new avenues are in sight for harnessing the light–matter interactions at room

temperature in the development of cavity spintronics and quantum technologies. METHODS EXPERIMENTAL DETAILS The planar microwave cavities are fabricated from Rogers RT/duroid 5880 High

Frequency Laminates. The relative permittivity of the substrate is 2.2, with a loss tangent of 0.0009. The substrate is 1.57 mm thick and covered by 17.5 μm thick copper layers on both

sides. An YIG sphere (M) with a diameter of 1 mm is attached to a Polytetrafluoroethylene rod which is transparent to microwaves. The rod is further connected to a stepping motor, so that

the position of YIG sphere can be precisely controlled to tune the coupling strength between the YIG sphere and the cavity. All the measurements are performed at room-temperature. The cavity

along with the YIG sphere as a whole hybrid system is immersed in a static external magnetic field. The _S_ 21 spectra of the hybrid system is obtained using a Vector Network Analyzer

(Agilent PNA N5230C) to measure the transmission signal of the cavity from port 1 to 2 with an input microwave power of −50 dBm. THEORETICAL DESCRIPTION The measured _S_ 21 spectra of the

A-P and P-M devices are analyzed by using input-output theory to determine the quality factor, gain, and coupling strength. The measured dispersions of the A-P-M hybrid system are

quantitatively and consistently explained by developing a model based on quantum theory. Without feedback photons, _N_ spins are collectively driven by the radiation field of the P-cavity

mode. When the gain of the A-cavity is switched on, in addition to the magnon-photon coupling that produces _m_ CMPs, the ensemble of CMP also collectively couples with the _n_ coherently

fedback photons. These two coherently linked cooperative dynamics are described by Eq. (2) in the main text, as well as by Supplementary Eq. 10. Based on this Hamiltonian, the quintuplet

dispersions and the feedback photon enhanced Rabi frequency are calculated. In the Supplementary Notes 4–6, the theoretical derivation and the quantum picture of both magnon–photon coupling

and polariton-photon coupling are explained in detail. DATA AVAILABILITY All relevant data are available from the authors. REFERENCES * Haroche, S. Controlling photons in a box and exploring

the quantum to classical boundary. _Rev. Mod. Phys._ 85, 1083 (2013). Article  ADS  CAS  Google Scholar  * Cohen-Tannoudji, C., Dupont-Roc, J. & Grynberg, G. _Atom-Photon Interactions_

(Wiley-VCH, 2004). * Huebl, H. et al. High cooperativity in coupled microwave resonator ferrimagnetic insulator hybrids. _Phys. Rev. Lett._ 111, 127003 (2013). Article  ADS  PubMed  CAS 

Google Scholar  * Tabuchi, Y. et al. Hybridizing ferromagnetic magnons and microwave photons in the quantum limit. _Phys. Rev. Lett._ 113, 083603 (2014). Article  ADS  PubMed  Google Scholar

  * Zhang, X., Zou, C. L., Jiang, L. & Tang, H. X. Strongly coupled magnons and cavity microwave photons. _Phys. Rev. Lett._ 113, 156401 (2014). Article  ADS  PubMed  CAS  Google Scholar

  * Goryachev, M. et al. High-cooperativity cavity QED with magnons at microwave frequencies. _Phys. Rev. Appl._ 2, 054002 (2014). Article  ADS  CAS  Google Scholar  * Bai, L. et al. Spin

pumping in electrodynamically coupled magnon-photon systems. _Phys. Rev. Lett._ 114, 227201 (2015). Article  ADS  PubMed  CAS  Google Scholar  * Haigh, J. A., Lambert, N. J., Doherty, A. C.

& Ferguson, A. J. Dispersive readout of ferromagnetic resonance for strongly coupled magnons and microwave photons. _Phys. Rev. B_ 91, 104410 (2015). Article  ADS  CAS  Google Scholar  *

Tabuchi, Y. et al. Coherent coupling between a ferromagnetic magnon and a superconducting qubit. _Science_ 349, 405 (2015). Article  ADS  CAS  PubMed  MATH  MathSciNet  Google Scholar  *

Wang, Y.-P. et al. Magnon Kerr effect in a strongly coupled cavity-magnon system. _Phys. Rev. B_ 94, 224410 (2016). Article  ADS  Google Scholar  * Yao, B. M. et al. Theory and experiment on

cavity magnon-polariton in the one-dimensional configuration. _Phys. Rev. B_ 92, 184407 (2015). Article  ADS  CAS  Google Scholar  * Harder, M., Bai, L., Match, C., Sirker, J. & Hu,

C.-M. Study of the cavity-magnon-polariton transmission line shape. _Sci. China Phys. Mech. Astronomy_ 59, 117511 (2016). Article  CAS  Google Scholar  * Cao, Y., Yan, P., Huebl, H.,

Goennenwein, S. T. & Bauer, G. E. Exchange magnon-polaritons in microwave cavities. _Phys. Rev. B_ 91, 094423 (2015). Article  ADS  CAS  Google Scholar  * Chiorescu, I., Groll, N.,

Bertaina, S., Mori, T. & Miyashita, S. Magnetic strong coupling in a spin-photon system and transition to classical regime. _Phys. Rev. B_ 82, 024413 (2010). Article  ADS  CAS  Google

Scholar  * Kohn, W. Cyclotron resonance and de Haas-van Alphen oscillations of an interacting electron gas. _Phys. Rev._ 123, 1242 (1961). Article  ADS  MATH  Google Scholar  * Hu, C. M.,

Batke, E., Köhler, K. & Ganser, P. Interaction coupled cyclotron transitions of two-dimensional electron systems in GaAs at high temperatures. _Phys. Rev. Lett._ 75, 918 (1995). Article

  ADS  CAS  PubMed  Google Scholar  * Maag, T. et al. Coherent cyclotron motion beyond Kohn’s theorem. _Nat. Phys._ 12, 119 (2016). Article  CAS  Google Scholar  * Hu, C.-M. Dawn of cavity

spintronics. _Phys. Canada_ 72, 76 (2016). Google Scholar  * Tabuchi, Y. et al. Quantum magnonics: the magnon meets the superconducting qubit. _Comp. R. Phys._ 17, 729 (2016). Article  CAS 

Google Scholar  * Zhang, X., Zou, C. L., Jiang, L. & Tang, H. X. Cavity magnomechanics. _Sci. Adv._ 2, e1501286 (2016). Article  ADS  PubMed  PubMed Central  Google Scholar  * Soykal, Ö.

O. & Flatté, M. E. Strong field interactions between a nanomagnet and a photonic cavity. _Phys. Rev. Lett._ 104, 077202 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Xu, X. et

al. Coherent optical spectroscopy of a strongly driven quantum dot. _Science_ 317, 929 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Dicke, R. H. Coherence in spontaneous radiation

processes. _Phys. Rev._ 93, 99 (1954). Article  ADS  CAS  MATH  Google Scholar  * Scheibner, M. et al. Superradiance of quantum dots. _Nat. Phys._ 3, 106 (2007). Article  CAS  Google Scholar

  * Noe, G. T. II et al. Giant superfluorescent bursts from a semiconductor magneto-plasma. _Nat. Phys._ 8, 219 (2012). Article  CAS  Google Scholar  * Agarwal, G. S. Vacuum-field Rabi

splittings in microwave absorption by Rydberg atoms in a cavity. _Phys. Rev. Lett._ 53, 1732 (1984). Article  ADS  CAS  Google Scholar  * Gui, Y. S., Wirthmann, A., Mecking, N. & Hu,

C.-M. Direct measurement of nonlinear ferromagnetic damping via the intrinsic foldover effect. _Phys. Rev. B_ 80, 060402 (2009). Article  ADS  CAS  Google Scholar  * Wang, Y.-P., Zhang, D.,

Li, T.-F., Hu, C.-M., & You, J. Q. Bistability of Cavity Magnon-Polaritons. Preprint at http://arxiv.org/abs/1707.06509v1 (2017). * Mollow, B. R. Power spectrum of light scattered by

two-level systems. _Phys. Rev_ 188, 1969 (1969). Article  ADS  Google Scholar  Download references ACKNOWLEDGEMENTS This work was funded by NSERC and NSFC (11429401) grants (C.M.H.). We

thank B.W. Southern, G.C. Tabisz, G. Bridges, and X.L. Gao for discussions. We would also like to acknowledge CMC Microsystems for providing equipments that facilitated this research. AUTHOR

INFORMATION AUTHORS AND AFFILIATIONS * Department of Physics and Astronomy, University of Manitoba, Winnipeg, Manitoba, Canada, R3T 2N2 Bimu Yao, Y. S. Gui, J. W. Rao, S. Kaur & C. -M.

Hu * State Key Laboratory of Infrared Physics, Chinese Academy of Sciences, Shanghai, 200083, China Bimu Yao, X. S. Chen & W. Lu * College of Science, Nanjing University of Aeronautics

and Astronautics, Nanjing, 210016, China Y. Xiao * Department of Physics, McGill University, Montréal, Québec, Canada, H3A 2T8 H. Guo * Department of Physics, St. Francis Xavier University,

Antigonish, Nova Scotia, Canada, B2G 2W5 K. -P. Marzlin * Department of Physics and Atmospheric Science, Dalhousie University, Halifax, Nova Scotia, Canada, B3H 4R2 K. -P. Marzlin Authors *

Bimu Yao View author publications You can also search for this author inPubMed Google Scholar * Y. S. Gui View author publications You can also search for this author inPubMed Google Scholar

* J. W. Rao View author publications You can also search for this author inPubMed Google Scholar * S. Kaur View author publications You can also search for this author inPubMed Google

Scholar * X. S. Chen View author publications You can also search for this author inPubMed Google Scholar * W. Lu View author publications You can also search for this author inPubMed Google

Scholar * Y. Xiao View author publications You can also search for this author inPubMed Google Scholar * H. Guo View author publications You can also search for this author inPubMed Google

Scholar * K. -P. Marzlin View author publications You can also search for this author inPubMed Google Scholar * C. -M. Hu View author publications You can also search for this author

inPubMed Google Scholar CONTRIBUTIONS B.M.Y. and Y.S.G. fabricated the devices, conducted the experiment and analyzed the data. B.M.Y. prepared all figures and wrote the Methods section.

J.W.R. and S.K. contributed to the device design and data analysis, respectively. W.L. and X.S.C. provided support and conceptual advice. Y.X. and C.M.H., in discussions with H.G. and

K.-P.M., developed the theory. C.-M.H. supervised the project, interpreted the results, and wrote the manuscript. All authors discussed the results and commented on the manuscript.

CORRESPONDING AUTHORS Correspondence to W. Lu or C. -M. Hu. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests. ADDITIONAL INFORMATION

PUBLISHER'S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. ELECTRONIC SUPPLEMENTARY MATERIAL SUPPLEMENTARY

INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution

and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if

changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the

material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to

obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS

ARTICLE Yao, B., Gui, Y.S., Rao, J.W. _et al._ Cooperative polariton dynamics in feedback-coupled cavities. _Nat Commun_ 8, 1437 (2017). https://doi.org/10.1038/s41467-017-01796-7 Download

citation * Received: 26 April 2017 * Accepted: 16 October 2017 * Published: 10 November 2017 * DOI: https://doi.org/10.1038/s41467-017-01796-7 SHARE THIS ARTICLE Anyone you share the

following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer

Nature SharedIt content-sharing initiative