Temperature-dependent elastic anisotropy and mesoscale deformation in a nanostructured ferritic alloy

ABSTRACT Nanostructured ferritic alloys are a new class of ultrafine-grained oxide dispersion-strengthened steels that have promising properties for service in extreme environments in future

nuclear reactors. This is due to the remarkable stability of their complex microstructures containing numerous Y-Ti-O nanoclusters within grains and along grain boundaries. Although

nanoclusters account primarily for the exceptional resistance to irradiation damage and high-temperature creep, little is known about the mechanical roles of the polycrystalline grains that

constitute the ferritic matrix. Here we report an _in situ_ mesoscale characterization of anisotropic responses of ultrafine ferrite grains to stresses using state-of-the-art neutron

diffraction. We show the experimental determination of single-crystal elastic constants for a 14YWT alloy, and reveal a strong temperature-dependent elastic anisotropy that leads to elastic

softening and instability of the ferrite. We also demonstrate, from anisotropy-induced intergranular strains, that a deformation crossover exists from low-temperature lattice hardening to

high-temperature lattice softening in response to extensive plastic deformation. You have full access to this article via your institution. Download PDF SIMILAR CONTENT BEING VIEWED BY

OTHERS REVEALING PER-GRAIN AND NEIGHBOURHOOD STRESS INTERACTIONS OF A DEFORMING FERRITIC STEEL VIA THREE-DIMENSIONAL X-RAY DIFFRACTION Article Open access 08 March 2024 NEUTRON DIFFRACTION

ANALYSIS OF STRESS AND STRAIN PARTITIONING IN A TWO-PHASE MICROSTRUCTURE WITH PARALLEL-ALIGNED PHASES Article Open access 11 August 2020 A QUINARY WTACRVHF NANOCRYSTALLINE REFRACTORY

HIGH-ENTROPY ALLOY WITHHOLDING EXTREME IRRADIATION ENVIRONMENTS Article Open access 02 May 2023 INTRODUCTION For high-temperature applications, polycrystalline grains can be detrimental in

structural materials, such as Ni-based superalloys, but they are beneficial for creep-resistant nanostructured ferritic alloys (NFAs)1,2,3. The ultrafine grains in NFAs remain unusually

stable with little or no grain growth, coarsening or recrystallization up to 800–900 °C. Although nanoclusters (NCs) and precipitates that are embedded in the grains and along the grain

boundaries4,5, together with solute segregation of W and Cr to the grain boundaries, are widely recognized to account for the excellent creep resistance2,4,6,7,8, the ultrafine ferrite

grains are also essential in promoting the mechanical strength, for example, via Hall-Petch hardening9. Thus, it is important to understand how the ferrite grains deform in response to

stresses, particularly, at elevated temperatures. When subjected to an applied load, each grain in a polycrystalline NFA behaves like a single crystal. It is known that a single crystal

exhibits elastic and plastic anisotropy, as its elastic stiffness and plastic strength depend on the crystallographic orientation. The mechanical response of a NFA grain, within a

polycrystalline NFA aggregate, is dependent on its single-crystal properties, the crystallographic orientation of its lattice and those of its neighbouring grains10. In particular, iron and

its alloys are among the most anisotropic body-centred cubic metals, for instance, <111> is the stiffest orientation that is ~2.2 times as strong as the most compliant <100>

orientation11. As such, in response to loading, differently oriented NFA grains will sustain distinctly different elastic strains and thus generate intergranular strains to maintain

compatibility with its neighbouring grains10,12. Plastic deformation starts within grains whose orientation, relative to the loading axis, facilitates the easy activation of their

dislocation slip systems when the critical resolved shear stress is reached; other oriented grains, which are plastically hard, will respond to the load elastically and sustain more loads

leading to stress redistribution among the grains. In the case of uniaxial tensile loading, the plastically deformed grains accumulate a compressive intergranular strain, whereas the grains

lying along the plastically hard orientations accommodate a tensile intergranular strain10,13. Thus, elastic anisotropy plays a predominant role in the early stage of plastic deformation,

particularly for the orientation dependence of dislocation slip activity14, while the anisotropy-induced intergranular strains contain unique information about the dislocation activities and

on the deformation processes12,13,15,16. As such, it is imperative to determine the elastic anisotropy and intergranular strains of NFAs to understand their grain-level anisotropic

deformation behaviours. In this study, we have characterized _in situ_ the mesoscale anisotropic responses of selected grains in a 14YWT NFA to uniaxial tensile loading at a broad range of

temperatures, by state-of-the-art neutron diffraction at the Spallation Neutron Source (SNS), Oak Ridge National Laboratory. From the responses to elastic deformation, the single-crystal

elastic constants of 14YWT were determined by considering the effect of preferred grain orientations (or texture), showing a strong temperature-dependent elastic anisotropy. From those in

response to extensive plastic deformation that manifest anisotropy-induced intergranular strains, a deformation crossover was evident from a low-temperature intragranular dislocation slip

mechanism to that mediated by grain boundary activities at elevated temperatures. RESULTS TENSILE DEFORMATION AT ELEVATED TEMPERATURES The material used in the present study was the

ultrafine-grained 14YWT NFA with a nominal composition of Fe-14Cr-0.16W-0.4Ti-0.14Y-0.4O (at.%) (see alloy synthesis in Methods). Atom probe tomography and transmission electron microscopy

characterizations showed that the 14YWT NFA has a grain size of 200–400 nm and contains a high number density of Y-Ti-O NCs (1-2 nm in diameter) inhomogeneously distributed in the grains and

along the grain boundaries4,17. As the alloy was made by hot-extrusion of mechanically alloyed powders, the 14YWT NFA tensile specimen exhibits a strong <110> fibre texture, as seen

from the neutron diffraction patterns and also consistent with the texture characterization in earlier works18. _In situ_ neutron diffraction characterization of the 14YWT NFA under uniaxial

tensile loading at room temperature (RT), 400, 600, 750 and 800 °C, respectively, was performed on VULCAN19, the Engineering Materials Diffractometer at the SNS (see Methods, Supplementary

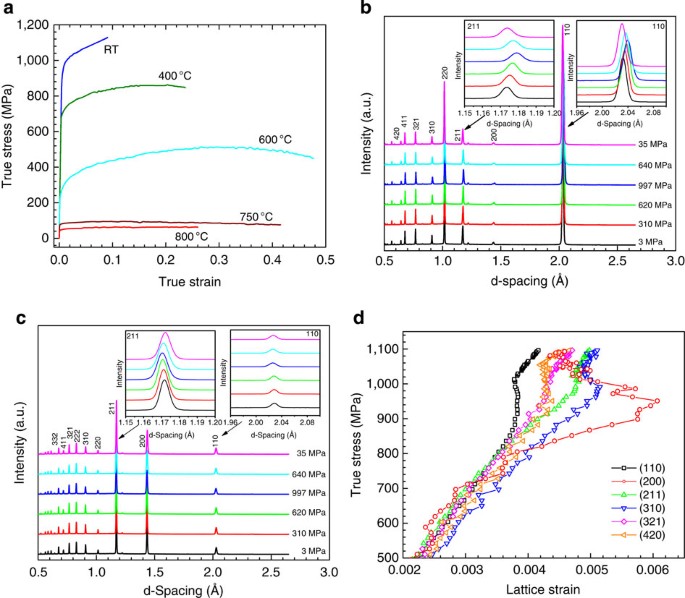
Figs 1–4 and Supplementary Note 1 for more details of the experimental setup). The observed true stress–true strain curve at each temperature is shown in Fig. 1a, and selected diffraction

patterns collected during tensile loading at RT are presented in Fig. 1b,c. The neutron scattering geometry (see Supplementary Fig. 1) allows for simultaneous measurements of two scattering

vectors Q1 and Q2, which are parallel and perpendicular to the tensile axis, respectively. Diffraction from the crystal lattice of grains whose plane normal (that is, <_hkl_>) is

parallel to Q1 or Q2 and satisfies Bragg’s law will be detected, and the lattice spacing (_d__hkl_) can thus be measured from the diffraction peak corresponding to the (_hkl_) reflection. If

treating the crystal lattice as a natural ‘atomic plane strain gauge’, lattice strains are determined from the shifts of lattice spacing due to an applied load, that is, where is the

stress-free reference lattice spacing. Accordingly, two lattice strain components, one parallel to the tensile axis (that is, the loading direction, LD) and the other perpendicular to the

tensile axis (that is, the transverse direction, TD), are measured simultaneously under tensile loading. As the macroscopic stress is uniaxial, only one stress component value is different

from zero (_σ_3 ≠ 0, LD → 3, TD → 1 where 1–3 refer to the three orthogonal axes). The two components of the grain-orientation-dependent strains recorded by our experimental setup are

designated as _ε_3(_hkl_) for the LD and _ε_1(_hkl_) for the TD. The generic _hkl_ indices denote not only a measurement direction in the crystal space, but also refer to specific families

of grain orientation. The family of grains whose plane normal <_hkl_> lies along the LD or the TD is designated as <_hkl_>//LD or <_hkl_>//TD, respectively. Figure 1d shows

the variation of true stress with the lattice strain for six <_hkl_>//LD families of grains obtained during tensile loading at RT. Thus, neutron diffraction serves as a grain selector

and can provide unique insights into the grain-scale deformation mechanisms. CRYSTALLOGRAPHIC TEXTURE Beside lattice-spacing shifts, diffraction peaks can be used to assess the preferred

orientation of grains (or texture). A virtual population of randomly oriented single crystals, generated by the quasi-Monte Carlo method, facilitates the realistic calculation of weighting

factors for different powder diffraction peaks detected by each of the two instrument detector banks at VULCAN, as well as the correlation between the peaks recorded in different banks. The

integrated intensities of a few independent diffraction peaks, after normalization to respective intensities obtained from a reference sample with random textures, are chosen to generate

inverse pole figures (IPFs) with respect to the LD and TD. For a _BCC_ structure, nine crystallographic directions define a network for texture index estimations, and the fundamental

triangle is partitioned in eight triangular cells (see Supplementary Fig. 5). The texture index inside each cell is defined using a barycentric interpolation method (see more details in

Supplementary Note 2). As the initial texture of the NFA specimens is expected to have the axial symmetry due to hot extrusion, and the tensile deformation preserves the same symmetry, the

IPFs allow for a complete texture description and can be efficiently used for averaging procedures in the analysis of stresses and strains. Two IPF maps with respect to the LD and TD are

depicted in Fig. 2a,b, respectively, showing clearly the presence of a strong <011> fibre texture in the NFA specimens before tensile loading (see more IPFs in Supplementary Figs 6 and

7). Under tensile loading, the <011>//LD fibre texture underwent a moderate strengthening. STRESS FACTORS AND SINGLE-CRYSTAL ELASTIC CONSTANTS To illustrate the elastic anisotropy and

intergranular strain accumulations in the NFA, the evolution of the lattice strains _ε_3(_hkl_) of several families of grains (<_hkl_>//LD) under RT tensile loading has been shown in

Fig. 1d. In the elastic regime, the lattice strain is linear as a function of the applied stress (_σ_3), where the slope represents the elastic stiffness at the grain level and manifests the

effect of cubic elastic anisotropy. Upon plastic deformation, the lattice strain begins to deviate from the elastic linearity and this effect is irreversible. The difference between the

current value of lattice strain and the value extrapolated from the elastic response (that is, the reversible part of the lattice strain) is termed as intergranular strain as mentioned

earlier, or Type II strain (ref. 11) and is conceptually equivalent with the residual strain recorded after unloading elastically from the current level of stress. In the following sections,

the focus is placed on analyzing the linear regime of the lattice strain evolution, in order to determine the single-crystal elastic constants that give rise to the elastic anisotropy at

different temperatures. In diffraction stress analysis for polycrystalline aggregates, there are two ways of approaching the strain response at the grain level. The first considers the

proportionality between the grain-level average normal strain components (measured by diffraction along certain single crystal directions) and the macroscopic stress components applied at

the specimen level. The proportionality factors are defined as ‘stress factors’. They can be calculated starting from single-crystal elastic constants by taking into account the

crystallographic texture and orientation stereology (that is, grain shape and packing) using various averaging techniques20,21,22,23,24. This approach was also consistently used to retrieve

the single-crystal elastic constants from polycrystalline diffraction data, especially when the texture influence is absent or weak. The second approach has been developed as a tool for

residual stress determination in deformed specimens after the external load is released. The macroscopic stress components are not known in this case; it is thus necessary to define a

mesoscopic average stress field depending on the grain orientations, known as the stress orientation distribution function25,26,27,28. In this case, the proportionality factors between the

strain and stress components are fully determined by the single-crystal elastic constants, although additional restrictive conditions or grain interaction models are often needed to obtain

physically consistent solutions for the stress field. In the present work, as the NFA specimens exhibit a strong <110> fibre texture as demonstrated in the preceding section, the

second approach has been applied to retrieve the single-crystal elastic constants from the _in situ_ neutron diffraction data. In this approach, the orientation-dependent stress acting at

the grain level is a free parameter, but, to reduce the number of parameters, the average local stress is considered to be uniaxial and parallel to the applied stress29. The FEM simulation

results reported by ref. 10 seem to support this assumption. As the analysis of lattice strains was performed in the elastic region only, the experimentally determined stress factors were

used as inputs in the model, while elasticity equations for single-crystals with cubic symmetry were applied for uniaxial straining30. In the elastic regime, the longitudinal lattice strain

component, _ε_3(_hkl_), is related to the applied stress through the stress factor _F_33(_hkl_), The transverse lattice strain, _ε_1(_h_′_k_′_l_′), can be represented as a sum of

transversally isotropic fibres with the <_h__i__k__i__l__i_> orientation along the LD, where _w_i is the volume fraction of the _i_th fibre, _f__i_(_h_′_k_′_l_′) the probability of

grains belonging to the _i_th fiber that has the <_h_′_k_′_l_′> direction along the TD, _F_13(_h_′_k_′_l_′,_h__i__k__i__l__i_) the stress factor for grains with <_h_′_k_′_l_′>

along the TD and < _h__i__k__i__l__i_ > along the LD, and > the average transverse stress factor. The average transverse stress factor, , or the longitudinal stress factor,

_F_33(_hkl_), can be determined from the slopes of the lattice strain [_ε_1(_h_′_k_′_l_′) or _ε_3(_hkl_)] versus true stress curves recorded during loading or unloading in the elastic regime

of deformation. Because of the strong initial <110> texture (that is, ~50% of the grains are oriented as <011>//LD), only six longitudinal stress factors could be determined in

the present work, and this number amounts to eight for the transverse stress factors. The _hkl_ stress factor distribution can be represented as an IPF map. For instance, the stress factor

IPFs collected at 400 °C are shown in Fig. 2c,d for LD and TD, respectively (see Supplementary Figs 8–10 and Supplementary Note 3 for other temperatures). The experimental values of stress

factors were obtained from averaging the measured slopes recorded during a few (2–4) loading/unloading cycles, as a systematic drift with the degree of plastic deformation was not

discernible (that is, slow texture development during loading). Stress factors can be calculated based on the single-crystal elasticity and by considering the adjustable stress concentration

factors that link the local stress field to the applied stress. As such, equations (1) and (2) can be written as where _p_i are the average stress concentration factors attached to

different texture fibres and In the above equations, _n_i and _m_i are the _hkl_ and _h_′_k_′_l_′ direction cosines in the cubic lattice cell, _S__ij_ and _c__ij_ the coefficients of

compliance and stiffness for the single crystal, and _A_ the anisotropy parameter. The basic fibres include <110>, <200>, <211>, <310>, <222>, <321>,

<411>, <420> and <332> along the LD, which are given in Supplementary Note 2 and represented in Supplementary Fig. 5. As the main fibre component contained almost 50% of

the grains aligned with the <011> generic direction along the LD, the _p_i values were treated differently for <011> and the rest of the components. The _p_i corresponding to

minor components (<001>, <013>, <012>, <112> and <123>) were correlated through a rational function of _F_(_n_) and the weighted average over all the _p_i

values was constrained to 1 (that is, the average stress is identical to the applied true stress). The values of single-crystal elastic constants were adjusted to minimize the squared

difference between the experimental stress factors values and the calculated ones. The IPFs were used to determine the volume fractions _w_i and the correlation factors _f_i(_m_j). Although

the influence of texture is generally challenging to quantify, the <011>//LD fibre texture, in this NFA, indeed facilitated the observation of the distinct difference in the transverse

stress factors between the <011> and <112> directions, as illustrated in Fig. 3. Following equation (4), if the tensile load is applied along the <110> direction, _D(n,m)_

varies from ½ to 0 and the corresponding transverse compliances change from positive to negative (see Fig. 3a). For ferritic steels, this peculiarity was recognized by ref. 31. Because of

the strong <011>//LD fibre texture, in our case, the transverse stress factor for the <110> direction can effectively go positive for large elastic anisotropy (Fig. 3b). The

single-crystal cubic elastic constants, _c_11, _c_12 and _c_44, have been deduced from the single-crystal compliances (_S_ij) by matching the experimental and calculated stress factors;

these values, together with the shear stiffness [_c_′=(_c_11 − _c_12)/2] and the elastic anisotropy parameter (_A_), are listed as a function of temperature in Table 1 and also shown in Fig.

4. Our estimation of relative errors of _S_11, _S_12 and S44 amounts to 2% or less for RT, 400 and 600 °C, but increases to 5% or more for 750 and 800 °C. A strong temperature-dependent

_c_′ and _A_ are evident as expected from those of pure Fe, which will be discussed in greater detail below. INTERGRANULAR STRAINS AND MESOSCALE DEFORMATION As indicated in Fig. 1d, the

<110>//LD grains are the first to yield and then take on compressive intergranular strains on plastic deformation at RT. This is also the case for other higher temperatures. The

intergranular strain accumulation in the <110>//LD grains thus contains mesoscale information characteristic of the plastic deformation. In what follows, we show how the <110>

intergranular strain accumulates as plastic deformation proceeds at various temperatures, which provide insights into the deformation mechanisms. The applied true stresses as a function of

lattice strain of the <110>//LD grains obtained at RT, 400, 600, 750 and 800 °C, respectively, are shown in Fig. 5. Intergranular strains (Δ_ε__II_) accumulated in the <110>//LD

grains (see the upper left inset of Fig. 5) are calculated by subtracting the current lattice strain (_ε_) from the projected linear elastic strain corresponding to the current applied

stress (_σ_), that is, where is the slope of the _σ_ versus _ε_ curve in the elastic regime at the temperature _T_. Normalized intergranular strain () as a function of normalized true stress

() for each of the five temperatures has been plotted in the lower right inset of Fig. 5, where is defined as the yield stress necessary for the <110>//LD grains to induce a plastic

strain of 50 × 10−6 and is the corresponding lattice strain. At low temperatures (RT and 400 °C), the <110> intergranular strain was accumulated gradually and became saturated at a

value of when the applied true stress increased continuously over ; this clearly depicts the initial yielding of the <110>//LD grains (fixed lattice strain and taking no more loads)

followed by strain hardening (increased lattice strain and taking on loads elastically). At the intermediate temperature (that is, 600 °C), the intergranular strain accumulation appears to

be similar to what underwent at low temperatures and also turned to be saturated but at a higher value of ; however, in sharp contrast, the intergranular strain saturation continued with a

decrease in the applied true stress from a value of . This behaviour indicates a mechanism of initial yielding followed by strain softening due to extensive plastic deformation. At high

temperatures (750 °C and 800 °C), intergranular strains were accumulated immediately after the onset of yielding but, strikingly, with the decrease in the applied true stress, indicative of

strain softening. DISCUSSION The experimentally determined anisotropy parameter (_A_) is shown in Fig. 4 as a function of temperature (_T_), which agrees remarkably well with the predictions

obtained from first-principles calculations by refs 32, 33. This result validates the above-mentioned method that was developed to extract elastic constants from textured polycrystalline

materials. The marked increase in _A_ at elevated temperatures is attributed to a sudden drop of the shear stiffness constant (_c_′) as _T_ approaches a critical value (Tc); this has been

depicted in the inset of Fig. 4, together with a best fit to the experimental data by the function: . Tc is determined to be 1,127 K (854 °C) for the NFA, in comparison with that of 1,185 K

(912 °C) for pure Fe with (ref. 34). For pure Fe, Tc is the bcc-fcc or _α_-_γ_ transition temperature as proved by ref. 34. The displacive _α_-_γ_ transition has been found to be associated

with the development of the (110) soft transverse acoustic phonon mode, corresponding to shear deformation of the BCC unit cell along the phase transformation pathway34,35,36,37. For the

14YWT NFA, however, the _α_-_γ_ transition and the presence of Tc are unexpected. Nevertheless, this transition was experimentally observed in the _in situ_ neutron diffraction studies of a

14YWT NFA, which showed a face-centred cubic _γ_-phase occurring at ~910 °C and then disappearing at ~810 °C when cooling from 1,300 °C to RT (see Supplementary Fig. 11). This transition is

likely when considering the Fe-Cr binary phase diagram, which exhibits an (_α_+_γ_) two-phase region between 11.2 wt.% Cr and 13.4 wt.% Cr ranging from ~846 °C up to 1,200 °C. Additions of

other alloying elements (for example, Y and Ti, and so on.) appear to widen the (_α_+_γ_) region; this makes 14YWT lying, most likely, in the vicinity of the _α_/(_α_+_γ_) boundary, as

indicated by the observed small volume fraction (that is, <1.5%) of the transformed _γ_ from neutron diffraction. Thus, the _α_-_γ_ transition in 14YWT appears to be marginal. However, no

matter how small the transformed-_γ_ amount is, the phase transition, if present, kinetically requires the whole _α_ phase (including every single α grain) to be elastically softening, so

as to facilitate the nucleation of _γ_ from _α_ with a specific crystallographic orientation relationship. This softening-associated phase transition provides a reasonable explanation of the

critical temperature Tc, as expected from our experimentally determined _c_′(_T_). Also shown in the inset of Fig. 4 is the 0.2% macroscopic yield strength (_σ__y_) determined from the

engineering stress–strain curves. Like _c_′, _σ__y_ exhibits a strong temperature dependency, particularly a considerable yield strength drop above 400 °C, which is consistent with previous

studies in the literature9,38,39. As described earlier, the yield strength is essentially determined by the grains whose orientation, relative to the loading axis, favours easy activation of

dislocation slip. For this NFA, the <110>//LD grains yield first upon plastic deformation; the microscopic yield strength () with respect to the <110>//LD grains also decreases

significantly as the temperature increases, as shown in Table 1. It is known that the dislocation character determines the onset of crystallographic slip, and the elastic energy factor (_K_)

of a dislocation may be considered as a strength indicator34,37. For example, the energy factor for straight edge dislocations with a Burgers vector of _a_‹100› and a dislocation line

direction of [001] (denoted here as 100[001]) can be evaluated as (refs 34, 37). The calculated _K_-values, as listed in Table 1, appear to scale with the yield strength, although _K_ shall

be slightly smaller (<10%) for temperatures below 600 °C where the _a_/2<111> dislocations (for example, ) dictate the yielding34. This behaviour suggests that, in addition to less

dispersion strengthening from the NCs and possible grain-boundary-mediated softening (for example, dislocation adsorption, and so on) at increased temperatures9, the yield strength drop

could be also induced by the reduction of the shear stiffness (_c_′) or, in other words, the large elastic anisotropy. Qualitatively, this finding may be understood in the framework of refs

34, 37 which showed that dislocation pile-ups can be markedly influenced by _c_′ when full anisotropic elasticity is considered. The anisotropy-induced intergranular strains/stresses in the

<110>//LD grains at RT, 400 and 600 °C show a nearly identical accumulation process during the onset of yielding and in the subsequent early-stage plastic deformation regime (see the

inset of Fig. 5). This intriguing similarity indicates that the same yielding mechanism is dominated by dislocation slip inside the grains, as manifested by the unaltered lattice strains and

the increased intergranular strains/stresses. However, at high temperatures from 750 to 800 °C, the onset of yielding is immediately followed by lattice softening as seen from decreased

lattice strains; this implies that these grains sustain less and less loads, and the plastic deformation is mediated by grain-boundary activities, although the Y-Ti-O NCs and vacancy-solute

interactions retard diffusion40. It is also noted that, in response to higher values of plastic deformation, a deformation crossover exists from low-temperature strain hardening to

high-temperature strain softening; the crossover temperature lies between 400 and 600 °C. This crossover phenomenon demonstrates that intragranular dislocation activities dictate the

late-stage of plastic deformation at low temperatures, whereas intergranular grain boundary activities are predominant at high temperatures. It should be noted that the volume fraction of

NCs in a 14YWT NFA can be estimated to be <0.1%, in consideration of their sizes of ~1-2 nm diameter with a number density of 1 × 1023 m−3 (refs 9, 17, 41). Moreover, these NCs have been

characterized to be coherent with the ferrite matrix5,17. Such a small volume fraction, together with the nanocluster-matrix coherency, would give rise to negligibly small misfit strains and

stress concentrations, if any, between NCs and the ferrite matrix during elastic deformation. Thus, NCs are believed to have insignificant effect on the single-crystal elastic constants of

the ferrite matrix. This may explain why there is no great difference in elastic constants between NFAs and Fe (or conventional steels), as assumed in many studies9. However, there has been

no direct measurement of the single-crystal elastic constants of NFAs to prove this hypothesis. In this regard, our diffraction results provide the first experimental evidence for validating

this scenario. In summary, anisotropic responses of the ultrafine 14 YWT NFA grains when subjected to tensile stresses at a broad range of temperatures were investigated using _in situ_

neutron diffraction. Temperature-dependent single-crystal elastic constants for the NFA were determined using a new model developed in the present work that takes into account the effect of

preferred grain orientations. A strong temperature-dependent elastic anisotropy is revealed as a result of a sharp decrease in the shear stiffness constant, indicating elastic softening and

instability of the ferritic matrix at elevated temperatures. The anisotropy-induced intergranular strain/stress accumulations reveal a crossover phenomenon of plastic deformation from a

low-T intragranular dislocation slip mechanism to that mediated by grain boundary activities at high-T. This study provides unique insights into the grain-level mesoscale deformation

mechanisms. METHODS ALLOY SYNTHESIS The 14YWT NFA was made by mechanical alloying of the mixture of Fe-Cr-W-Ti alloy powder and Y2O3 powder, followed by canning in an evacuated jacket and

hot extrusion at 850 °C. The hot-extruded ingot was then annealed for 1 h at 1,000 °C. One heat was used to produce this NFA, whose nominal composition is Fe-14Cr-0.16W-0.4Ti-0.14Y-0.4O

(at.%). The details of alloy processing have been described elsewhere2. NEUTRON DIFFRACTION EXPERIMENTAL SETUP _In situ_ neutron diffraction experiments were performed on VULCAN19, the

Engineering Materials Diffractometer at the SNS, Oak Ridge National Laboratory. Threaded dogbone-shaped NFA specimens of 2.90 mm in diameter and 20.6 mm in gauge-length were uniaxially

deformed under tension using a Materials Testing System load-frame. The macroscopic engineering strain for the measurement at RT was recorded by an extensometer with a nominal gauge length

of 12.7 mm. An induction heater attached to the load-frame was used for heating each specimen to a preset temperature, at which tensile loading of the specimen was conducted while being

monitored _in situ_ by neutron diffraction (see Supplementary Fig. 2). Four fine-gauge _K_-type thermocouples were spot weld onto each specimen to control and monitor the temperatures at

locations near the specimen centre and the two ends. A uniform temperature zone of ~10 mm in the centre of each specimen was established by fine-tuning the induction heater before loading.

This homogeneous zone, having a temperature gradient of <3 °C and being the hottest part of the specimen, was probed _in situ_ by the neutron beam under tensile loading with a strain rate

of ~8 × 10−5 s−1. True stresses and true strains during plastic deformation at high temperatures were evaluated from measured engineering stresses, together with engineering strains

estimated from the relative cross-head displacements after a linear correction (see more details in Supplementary Note 1). As shown in Supplementary Fig. 1, the tensile stress axis of the

load-frame was mounted at 45° from the incident neutron beam direction. Diffraction patterns were recorded by the two detector banks (namely, B1 and B2) positioned at diffraction angles of

−/+90°. As such, B1 and B2 collected diffraction from the lattice planes perpendicular and parallel to the LD, respectively. The sampling volume was defined by the incident beam slits (5 mm

width and 3 mm height) and the radial collimators located between the specimen and the detector banks restricting the field of view to 5 mm along the neutron beam path. The neutron

diffraction data were collected continuously during the tensile loading at various temperatures. By using the data reduction software VDRIVE42, the recorded data were then ‘sliced’ and

binned into histograms corresponding to small temporal intervals that were synchronized with the loading parameters (force, displacement, temperature, and so on.). Single–peak fitting,

employing the GSAS program in VDRIVE, was used to extract the peak position, width and intensity corresponding to each _hkl_ reflection. More details about the neutron diffraction

experimental setup are available in Supplementary Note 1. ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE: Stoica, G. M. _et al._ Temperature-dependent elastic anisotropy and mesoscale

deformation in a nanostructured ferritic alloy. _Nat. Commun._ 5:5178 doi: 10.1038/ncomms6178 (2014). REFERENCES * Zinkle, S. J. & Busby, J. T. Structural materials for fission &

fusion energy. _Mater. Today_ 12, 12–19 (2009). Article  CAS  Google Scholar  * Hoelzer, D. T. et al. Influence of particle dispersions on the high-temperature strength of ferritic alloys.

_J. Nucl. Mater._ 367, 166–172 (2007). Article  ADS  Google Scholar  * Miller, M. K., Parish, C. M. & Li, Q. Advanced oxide dispersion strengthened and nanostructured ferritic alloys.

_Mater. Sci. Tech._ 29, 1174–1178 (2013). Article  CAS  Google Scholar  * Yao, L., Ringer, S. P., Cairney, J. M. & Miller, M. K. The anatomy of grain boundaries: Their structure and

atomic-level solute distribution. _Scripta Mater._ 69, 622–625 (2013). Article  CAS  Google Scholar  * Hirata, A. et al. Atomic structure of nanoclusters in oxide-dispersion-strengthened

steels. _Nat. Mater._ 10, 922–926 (2011). Article  ADS  CAS  PubMed  Google Scholar  * Fu, C. L., Krcmar, M., Painter, G. S. & Chen, X. Q. Vacancy mechanism of high oxygen solubility and

nucleation of stable oxygen-enriched clusters in Fe. _Phys. Rev. Lett._ 99, 225502 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Brandes, M. C., Kovarik, L., Miller, M. K., Daehn, G.

S. & Mills, M. J. Creep behavior and deformation mechanisms in a nanocluster strengthened ferritic steel. _Acta Mater._ 60, 1827–1839 (2012). Article  CAS  Google Scholar  * Schneibel,

J. H. et al. Ultrafine-grained nanocluster-strengthened alloys with unusually high creep strength. _Scripta Mater._ 61, 793–796 (2009). Article  CAS  Google Scholar  * Schneibel, J. H.,

Heilmaier, M., Blum, W., Hasemann, G. & Shanmugasundaram, T. Temperature dependence of the strength of fine- and ultrafine-grained materials. _Acta Mater._ 59, 1300–1308 (2011). Article

  CAS  Google Scholar  * Wong, S. L. & Dawson, P. R. Influence of directional strength-to-stiffness on the elastic-plastic transition of fcc polycrystals under uniaxial tensile loading.

_Acta Mater._ 58, 1658–1678 (2010). Article  CAS  Google Scholar  * Hutchings, M. T., Withers, P. J., Holden, T. M. & Lorentzen, T. _Introduction to the characterization of residual

stress by neutron diffraction_ Taylor&Francis (2005). * Pang, J. W. L., Holden, T. M., Turner, P. A. & Mason, T. E. Intergranular stresses in Zircaloy-2 with rod texture. _Acta

Mater._ 47, 373–383 (1999). Article  CAS  Google Scholar  * Pang, J. W. L., Holden, T. M. & Mason, T. E. In situ generation of intergranular strains in an A17050 alloy. _Acta Mater._ 46,

1503–1518 (1998). Article  CAS  Google Scholar  * Clausen, B., Lorentzen, T. & Leffers, T. Self-consistent modelling of the plastic deformation of FCC polycrystals and its implications

for diffraction measurements of internal stresses. _Acta Mater._ 46, 3087–3098 (1998). Article  CAS  Google Scholar  * Holden, T. M., Holt, R. A. & Pang, J. W. L. Intergranular stresses

in ZIRCALOY-2. _Metall. Mater. Trans. A_ 33, 749–755 (2002). Article  Google Scholar  * Daymond, M. R., Tome, C. N. & Bourke, M. A. M. Measured and predicted intergranular strains in

textured austenitic steel. _Acta Mater._ 48, 553–564 (2000). Article  CAS  Google Scholar  * Brandes, M. C., Kovarik, L., Miller, M. K. & Mills, M. J. Morphology, structure, and

chemistry of nanoclusters in a mechanically alloyed nanostructured ferritic steel. _J. Mater. Sci._ 47, 3913–3923 (2012). Article  ADS  CAS  Google Scholar  * Praud, M. et al. Study of the

deformation mechanisms in a Fe-14% Cr ODS alloy. _J. Nucl. Mater._ 428, 90–97 (2012). Article  ADS  CAS  Google Scholar  * Wang, X. L. et al. VULCAN–The engineering diffractometer at the

SNS. _Phys. B_ 385, 673–675 (2006). Article  ADS  Google Scholar  * Gnaeupel-Herold, T., Brand, P. C. & Prask, H. J. Calculation of single-crystal elastic constants for cubic crystal

symmetry from powder diffraction data. _J. Appl. Cryst._ 31, 929–935 (1998). Article  Google Scholar  * Howard, C. J. & Kisi, E. H. Measurement of single-crystal elastic constants by

neutron diffraction from polycrystals. _J. Appl. Cryst._ 32, 624–633 (1999). Article  CAS  Google Scholar  * Bunge, H. J., Kiewel, R., Reinert, T. & Fritsche, L. Elastic properties of

polycrystals–influence of texture and stereology. _J. Mech. Phys. Solids_ 48, 29–66 (2000). Article  ADS  MathSciNet  Google Scholar  * Matthies, S., Priesmeyer, H. G. & Daymond, M. R.

On the diffractive determination of single-crystal elastic constants using polycrystalline samples. _J. Appl. Cryst._ 34, 585–601 (2001). Article  CAS  Google Scholar  * Gnaeupel-Herold, T.,

Creuziger, A. A. & Iadicola, M. A model for calculating diffraction elastic constants. _J. Appl. Cryst._ 45, 197–206 (2012). Article  CAS  Google Scholar  * Behnken, H. Strain-function

method for the direct evaluation of intergranular strains and stresses. _Phys. Stat. Solidi A_ 177, 401–418 (2000). Article  ADS  CAS  Google Scholar  * Popa, N. C. & Balzar, D. Elastic

strain and stress determination by Rietveld refinement: generalized treatment for textured polycrystals for all Laue classes. _J. Appl. Cryst._ 34, 187–195 (2001). Article  CAS  Google

Scholar  * Wang, Y. D., Wang, X. L., Stoica, A. D., Richardson, J. W. & Peng, R. L. Determination of the stress orientation distribution function using pulsed neutron sources. _J. Appl.

Cryst._ 36, 14–22 (2003). Article  Google Scholar  * DeWit, R. Diffraction elastic constants of a cubic polycrystal. _J. Appl. Cryst._ 30, 510–511 (1997). Article  CAS  Google Scholar  *

Ungar, T., Stoica, A. D., Tichy, G. & Wang, X. L. Orientation-dependent evolution of the dislocation density in grain populations with different crystallographic orientations relative to

the tensile axis in a polycrystalline aggregate of stainless steel. _Acta Mater._ 66, 251–261 (2014). Article  CAS  Google Scholar  * Norris, A. N. Poisson's ratio in cubic materials.

_Proc. R. Soc. A_ 462, 3385–3405 (2006). Article  ADS  MathSciNet  Google Scholar  * Oliver, E. C., Daymond, M. R. & Withers, P. J. Interphase and intergranular stress generation in

carbon steels. _Acta Mater._ 52, 1937–1951 (2004). Article  CAS  Google Scholar  * Razumovskiy, V. I., Ruban, A. V. & Korzhavyi, P. A. Effect of temperature on the elastic anisotropy of

pure Fe and Fe0.9Cr0.1 random alloy. _Phys. Rev. Lett._ 107, 205504 (2011). Article  ADS  CAS  PubMed  Google Scholar  * Zhang, H. L. et al. Elastic anomalies in Fe-Cr alloys. _J.

Phys.Condes. Matter_ 25, 195501 (2013). Article  ADS  Google Scholar  * Dudarev, S. L., Bullough, R. & Derlet, P. M. Effect of the alpha-gamma phase transition on the stability of

dislocation loops in bcc iron. _Phys. Rev. Lett._ 100, 135503 (2008). Article  ADS  CAS  PubMed  Google Scholar  * Hasegawa, H., Finnis, M. W. & Pettifor, D. G. A calculation of

elastic-constants of ferromagnetic iron at finite temperatures. _J. Phys. F_ 15, 19–34 (1985). Article  ADS  CAS  Google Scholar  * Hasegawa, H., Finnis, M. W. & Pettifor, D. G. Phonon

softening in ferromagnetic bcc iron. _J. Phys. F_ 17, 2049–2055 (1987). Article  ADS  CAS  Google Scholar  * Fitzgerald, S. P. & Dudarev, S. L. Dislocation pile-ups in Fe at high

temperature. _Proc. R. Soc. A_ 464, 2549–2559 (2008). Article  ADS  CAS  Google Scholar  * Kim, J. H., Byun, T. S., Hoelzer, D. T., Kim, S. W. & Lee, B. H. Temperature dependence of

strengthening mechanisms in the nanostructured ferritic alloy 14YWT: Part I-Mechanical and microstructural observations. _Mater. Sci. Eng. A_ 559, 101–110 (2013). Article  CAS  Google

Scholar  * Kim, J. H. et al. Temperature dependence of strengthening mechanisms in the nanostructured ferritic alloy 14YWT: Part II-Mechanistic models and predictions. _Mater. Sci. Eng. A_

559, 111–118 (2013). Article  CAS  Google Scholar  * Miller, M. K., Fu, C. L., Krcmar, M., Hoelzer, D. T. & Liu, C. T. Vacancies as a constitutive element for the design of

nanocluster-strengthened ferritic steels. _Front. Mater. Sci. China_ 3, 9–14 (2009). Article  ADS  Google Scholar  * Miller, M. K., Russell, K. F. & Hoelzer, D. T. Characterization of

precipitates in MA/ODS ferritic alloys. _J. Nucl. Mater._ 351, 261–268 (2006). Article  ADS  CAS  Google Scholar  * An, K. et al. First in situ lattice strains measurements under load at

VULCAN. _Metall. Mater. Trans. A_ 42, 95–99 (2011). Article  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS This research was supported by the US Department of Energy, Division of

Materials Sciences and Engineering. The neutron scattering work at the SNS was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, US Department of

Energy, at Oak Ridge National Laboratory under contract DE-AC05-00OR22725 with UT-Battelle. The authors (G.M.S. and D.M.) thank Dr E.A. Payzant for useful discussions. A.D.S. and D.M.

acknowledge the conceptual contribution of Professor X.-L. Wang (City University Hong Kong) to the early stage of this study. We also thank Harley Skorpenske for technical support at VULCAN.

AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Chemical and Engineering Materials Division, Spallation Neutron Source, Oak Ridge National Laboratory, Oak Ridge, 37831-6139, Tennessee, USA

G.M. Stoica, A.D. Stoica & D. Ma * Center for Nanophase Materials Sciences, Oak Ridge National Laboratory, Oak Ridge, 37831-6139, Tennessee, USA M.K. Miller Authors * G.M. Stoica View

author publications You can also search for this author inPubMed Google Scholar * A.D. Stoica View author publications You can also search for this author inPubMed Google Scholar * M.K.

Miller View author publications You can also search for this author inPubMed Google Scholar * D. Ma View author publications You can also search for this author inPubMed Google Scholar

CONTRIBUTIONS G.M.S., A.D.S. and D.M. designed and performed the experiments and analysed the data. D.M. coordinated the scattering experiments. M.K.M. developed and supervised the research

programme, selected and provided additional microstructural data of the 14YWT NFA. A.D.S. and D.M. wrote the manuscript after discussions and with contributions from all the authors.

CORRESPONDING AUTHOR Correspondence to D. Ma. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests. SUPPLEMENTARY INFORMATION SUPPLEMENTARY

INFORMATION Supplementary Figures 1-11, Supplementary Notes 1-3 and Supplementary References (PDF 1099 kb) RIGHTS AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS

ARTICLE Stoica, G., Stoica, A., Miller, M. _et al._ Temperature-dependent elastic anisotropy and mesoscale deformation in a nanostructured ferritic alloy. _Nat Commun_ 5, 5178 (2014).

https://doi.org/10.1038/ncomms6178 Download citation * Received: 27 February 2014 * Accepted: 08 September 2014 * Published: 10 October 2014 * DOI: https://doi.org/10.1038/ncomms6178 SHARE

THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to

clipboard Provided by the Springer Nature SharedIt content-sharing initiative