Quantitative genetics of allogamous f2: an origin of randomly fertilized populations

ABSTRACT The quantitative genetic properties are derived for the bulk F2 originating from random fertilization (RF) amongst hybrid (F1) individuals. Only its mean appears to have been

derived previously, and that definition is confirmed (by another method). New general equations are found also for all genotype frequencies, allele frequencies, inbreeding coefficient, the

genotypic, additive-genetic and dominance variances, and broad-sense and narrow-sense heritabilities. The assumption that such an F2 is a classical RF population is shown to be correct.

Indeed, the allogamous F2 is a natural origin for the RF population. The relationships are given between precedent RF populations (parents) and subsequent RF populations following

hybridization (allogamous F2). The allogamous F2 is generally inbred with respect to its parental F1, the degree depending on the hybrid’s parents’ allele frequencies. At the same time, it

is _outbred_ with respect to those original parents, and not inbred at all with respect to the equivalent RF population. The genotypic variance is generally more than in the F1, and likewise

for heritabilities. These findings make it possible to evaluate the genetic advance from selection and hybridization. The results depend on the allele frequencies of the original parents

and the degree of overdominance, but generally, selection is more advantageous than hybrid vigour. SIMILAR CONTENT BEING VIEWED BY OTHERS HOW DID MENDEL ARRIVE AT HIS DISCOVERIES? Article 11

July 2022 DETECTING PURGING OF INBREEDING DEPRESSION BY A SLOW RATE OF INBREEDING FOR VARIOUS TRAITS: THE IMPACT OF ENVIRONMENTAL AND EXPERIMENTAL CONDITIONS Article 26 April 2021

CORRELATIONAL SELECTION IN THE AGE OF GENOMICS Article 15 April 2021 INTRODUCTION Many episodes in evolution and plant breeding are initiated by hybridizing between parent populations or

individuals. Meiosis and syngamy within the hybrid (F1) lead to a population with a different frequency structure (the F2), i.e. the F1 is in disequilibrium and has an ephemeral population

structure. The quantitative genetic properties of the F1 population have been examined (Gordon, 1999), but how do the properties of the emergent F2 relate to these? Intuitively, because of

meiosis, we would expect more variance: but we need to explore the quantitative relationships of this matter. Intuitively, also, we would expect to have to account for effects of inbreeding

because of shared ancestral origins (F1 individuals) amongst members of the F2 population. This needs to be reconciled with the assumption that an allogamous F2 can be considered as a single

panmictic random fertilizing gamodeme with zero inbreeding. It appears that these, and related, matters have not been explored rigorously nor quantitatively. These omissions became strongly

apparent when the author sought to estimate the genetic advance arising from selection from an F2. This is a fundamental phase in important protocols of plant breeding, such as Line

Breeding and Pedigree Breeding (Allard, 1960; Poehlmann, 1979; Moore and Janik, 1983). Such selection from the F2 is essential also to the ongoing contribution of a hybrid in natural

selection. In order to evaluate genetic advance from such selection, we need more knowledge on the properties of the F2. The present paper examines the quantitative genetic properties of the

bulk F2 population generated by random fertilization amongst F1 individuals. Some earlier focus has examined the mean of such an F2 (Falconer, 1981), in order to demonstrate the drop in

hybrid vigour compared with the F1. Here, we derive as well the allogamous F2 genotypic variance (σ2G), genic variance (σ2A), dominance variance (σ2D), broad-sense and narrow-sense

heritabilities (_h_2B and _h_2N, respectively), genotypic and allelic frequencies, and levels of inbreeding. Following this, we will be able to estimate selection genetic advance from the F2

and we will examine the relationship of the allogamous F2 to random fertilizing (RF) populations. GENERAL METHOD A population consists of genotypes arising from alleles (or allele

Expectations) _A_1 and _A_2 present with frequencies _p_ and _q_ respectively, with no omissions (i.e. _p_ + _q_=1). Its individual phenotypic Expectations are its genotype effects defined

as deviates from the homozygote midpoint, namely G′=[_a_, _d_, −_a_] for {_A_1_A_1, _A_1_A_2, _A_2_A_2}, respectively. This is the familiar single-factor gene model used to define classical

RF populations (Falconer, 1981). It has been used also to define hybrids (Gordon, 1999), where further discussion is presented on its utility. In examples given in this paper, we will use

_a_=10, and _d_=7.5 (partial dominance). The population properties also depend on the genotype frequencies; it is one of the tasks of this paper to discover these for the allogamous F2. The

original parent populations set the parameters not only for the hybrid (F1), but also for this F2. The _focal_ parent (P1) is a population of individuals, with allele frequencies _p_1 and

_q_1. As _p_1 → 1 (or 0), we are dealing with a pure-line population (or even a homozygous individual); but a focal-parent population may have any _p_1 within the range 0 ≤ _p_1 ≤ 1. The

_other_ parent (P2) has frequencies defined as _offsets_ from the P1 frequencies, following Falconer (1981). This leads to _p_2=_p_1 − _y_, and _q_2=_q_1 + _y_, where _y_=_p_1 − _p_2. These

are the same definitions as used for hybrids (Falconer, 1981; Gordon, 1999). The RF population analogous to the allogamous F2 is of special relevance, and is based on p F 1 = p 1 - 1 2 y and

q F 1 = q 1 - 1 2 y (Gordon, 1999). It has the classical properties (Falconer, 1981): A major task of this paper is to redefine these in terms of the F2 ‘offset’ parameters, and to compare

the two sets of results. All other Methods form an integral part of the derivations which constitute the Results of this paper, and will be presented there. RESULTS GENOTYPE FREQUENCIES

ALLOGAMOUS F2 We adopt a fundamental means of deriving the genotype frequencies: we use the F1 genotype frequencies (Gordon, 1999) as parental frequencies, and the cross-products of these

form crossing (mating) frequencies. Next, we note the segregation ratios of each family of cross which, when multiplied by the crossing frequencies, gives the family frequencies of

segregating progeny genotypes. When these terms are accumulated across all crossing families, we obtain the allogamous F2 genotype frequencies. The F1 parent frequencies and the crossing

frequencies are presented in Table 1. Gathering the outcomes for _A_1_A_1 progenies leads to: Similarly, for _A_1_A_2 progenies: And lastly, for _A_2_A_2 progenies: We define the row-vector

containing these results as F′. These results reveal that for any allogamous F2 from crosses with _complementary opposite_ parents (i.e. _p_2=1 − _p_1), the heterozygote frequency is

constant (F12=0.5) across all values of _p_1. Whenever the _other_ parent has a _fixed p_2, the general levels of heterozygosity are often lower than for the _complementary opposites_ cases.

The heterozygosity of _any_ F2 is generally less than that in its corresponding F1; but the two are equal when _p_1=_p_2. EQUIVALENT RF AND PANMICTIC Here, we use the classical RF genotype

frequencies, and substitute (_p_1 − ½_y_) for p F 1 and (_q_1 + ½_y_) for q F 1 (Gordon, 1999). Thus: We notice that these are the same results as obtained for the allogamous F2, proving

that the genotype frequencies at least are the same for the two situations. Note that these two results were derived in different but relevant ways, and obtaining the same outcome

establishes their equivalence. ALLELE FREQUENCIES We need to check the allele frequencies of the F2 using the genotype frequencies F′. This can be done as weighted means using the allele

structures of genotypes as weights. Thus, for the _A_1 allele, the weights are W′1=[1, 1/2, 0] for {_A_1_A_1, _A_1_A_2, _A_2_A_2}, respectively; and for the _A_2 allele, the respective

weights are W′2=[0, 1/2, 1]. The allele frequencies are then found as follows: and Note that these are the same as the F1 frequencies (Gordon, 1999), which we would expect. (The RF

frequencies were defined to these values at the outset). INBREEDING COEFFICIENT The natural inbreeding reference population for the F2 is the F1, as the former is sexually derived from the

latter. The F2 bulk population is a mixture of many different full-sib lines and half-sib lines, with varying degrees of coancestry amongst them. The simplest approach to defining inbreeding

in this bulk mixture is the net drop in heterozygosity of the F2 relative to the F1. This approach precludes any need to unravel the breeding system mixture. Furthermore, it automatically

reflects the dynamics of the bulk which depend on the parental inputs (_p_1). Therefore, the inbreeding coefficient is defined as: where _f_12 of the F2 is defined in this paper, and _f_12

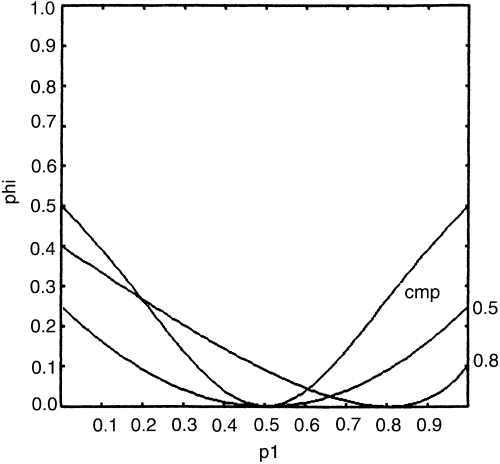
of the F1 is defined in Gordon (1999). The degree of inbreeding in the allogamous F2, for all possible focus-parent inputs (_p_1), is visualized in Fig. 1, where the other-parent is

_complementary opposite_ or _fixed p_2=0.01, 0.5 or 0.8 as examples. We observe that the level of inbreeding depends on the relatives-mixture present in the F1 bulk, which changes as does

_p_1. Where _p_1 → 0 (or 1), for _complementary opposite crosses_, the hybrid is virtually entirely heterozygous, and the F2 is equivalent to selfing a heterozygote; hence the inbreeding is

φ → ½. Again, for this same crossing system, when _p_1 → _p_2 → ½, the ‘hybrid’ is virtually a RF population, and the F2 is equivalent to a second-generation RF in equilibrium with the

‘hybrid’. Therefore, there is no change in heterozygosity, and φ → 0. Now, we will compare this F2 heterozygosity against that of the equivalent RF, as an alternative reference. This is

achieved simply by replacing _f_12 of the F1 with _f_12 of the RF in the equation for φ. We recall that we have shown that both the allogamous F2 and the equivalent RF (based on p F 1 ) have

the same level of heterozygosity. Therefore, the inbreeding of the allogamous F2 is zero when referenced against the equivalent RF population. This conforms with widespread notions already

extant. But it is of doubtful relevance, because the _natural reference_ population is the parental origin, viz. the F1. The whole issue becomes more intriguing still if we use the _mean

heterozygote frequency of the two parents_ as the reference basis. We then find that nearly all allogamous F2 are _outbred_ (negative φ) with respect to the parents, except at _p_1 → ½. This

dependence of the value of inbreeding on an appropriate reference base was noted by its pioneer, Sewall Wright (Wright, 1921). POPULATION MEAN ALLOGAMOUS F2 The F2 mean (_F¯_2) is μ+ G ¯ F

2 , where μ is the attribute background mean, and G ¯ F 2 (=γ also) is the gene-model mean. The latter is obtained as follows: The α1 is the usual _average allele substitution effect_ for

the focal parent population (e.g. Falconer, 1981), and equals _a_ + (_q_1 − _p_1)_d_. This is the same result as presented by Falconer (1981) using another method of derivation, and the

−½_y_2_d_ represents the drop in hybrid vigour, which was his focus. Several examples of this mean are shown in Fig. 2, all for partial dominance (_a_=10, _d_=7.5, μ=10). Figure. 2 shows

both _complementary opposite parents_ and _fixed other-parent p_2=0.5, and compares both the F2 and F1 means. The loss of vigour is obvious, especially for _p_1 → 0 (or 1). Two other F2-mean

examples are shown to illustrate extremes, namely _fixed p_2=0.01 and _fixed p_2=0.8. It is interesting to note the patterns of increase in the mean with increasing overdominance. The

effect of _parental complementarity_ (i.e. p F 1 = ½ always) leads to the mean being constant across all _p_1, but rising in steps with increasing overdominance. The patterns with other

forms of parental relationship (with respect to _p_1 and _p_2) are more varied, but there is still a general increase in the mean with increasing overdominance. EQUIVALENT RF AND PANMICTIC

We use at once the classical RF definition of the gene-model mean (see General Method), and substitute into it the values for p F 1 in _offset_ form. Thus: Through this appropriate

independent derivation, we find that the RF mean is the same as the F2 mean. We now have proved that in two properties the allogamous F2 and the RF population are identical, viz. _genotype

frequencies_ and _gene-model mean_. GENOTYPIC VARIANCE ALLOGAMOUS F2 The allogamous F2 genotypic variance has the Expectation where the right-hand terms are an unadjusted sum-of-squares

(USS) and a correction factor (CF), respectively. Using the previously defined F′ and G′ vectors and the scalar γ, and after subtracting the CF from the USS followed by gathering and

factoring several terms Footnote 1, the SS (i.e. σ2G the genotypic variance Footnote 2), becomes: Now, recalling the classical definitions of σ2A, and of σ2D (Falconer, 1981), and of

cov(_ad_) and σ2d, (Gordon, 1999), this whole expression resolves into: The previous equation (eqn 2) is simpler, but this one provides some link with the traditional nomenclature. However,

there is some danger in it, for these components are _not_ the genic and dominance variances of the F2 σ2G. We will explore that issue in due course. The variance can be visualized for our

partial dominance and _complementary opposites_ and _fixed other-parent p_2=_½_ crosses in Fig. 3. In each case, it is compared also with the σ2G of its F1. Notice from Fig. 3 that this F2

variance is generally greater than that of its F1, except for the region _p_1 → ½ where they are virtually equal. This was one of the questions we posed at the beginning. For the

_complementary opposites cross_, the F2 variance greatly exceeds that of its F1 as _p_1 → 0 (or 1). Another conspicuous result for the _complementary opposites_ is that the variance is

constant across all _p_1; this results from the facts that _p_F1 is always ½, and F2 genotype frequencies are constant for such crosses. The results for the _fixed p_2=_½_ crosses are

conspicuously different. These general differences between the F2 and F1 variances have interesting consequences regarding ongoing selection efficiency, and the balances between selection

and hybrid vigour, which we will discuss later. EQUIVALENT RF AND PANMICTIC As before, we establish an independent derivation by using the classical RF approach, and substitute into it the

offset p F 1 structures. Therefore, for the RF base σ2G=σ2A+σ2D, where σ2A is the genic variance and σ2D is the dominance variance. We define each of these separately, and accumulate them at

the end. (I) GENIC VARIANCE Substituting previous definitions of σ2A, α, σ2d, cov(_a_,_d_) into this, it becomes: It is convenient subsequently to leave the several σ2d terms separated

rather than gathered together. We can note immediately that this equation converts the genic variance of one RF population (the focal parent) into the genic variance of another RF population

(the p F 1 equivalent), which presages things to come. Notice that this genic variance absorbs several genetical terms, involving not only the _focal parent genic variance_, but also

cov(_a_,_d_), _average allele substitution effect_ (α), _gene-model homozygote effect_ (_a_), and much of the _gene-model heterozygote variance_ (σ2d) Footnote 3. Definitely, this is not

simple in terms of the gene-model interpretation; but this difficulty extends to the widely accepted classical (RF) genic variance as well. (II) DOMINANCE VARIANCE After substituting

previous definitions of σ2D and σ2d this becomes: As previously, it is convenient to leave the σ2d terms separated. Once again, we have a conversion equation from one RF (parental) to

another RF (hybrid equivalent). Notice that this dominance variance collects together all of the _gene-model heterozygote variance_ (σ2d) not absorbed into the genic variance. It can be

shown that this occurs also in the classical definition of dominance variance. (III) GENOTYPIC VARIANCE Upon accumulating eqns (5) and (7), four cancellations occur (terms 2, 3, 4 and 5 of

eqn 7 with respective terms 7, 8, 9 and 10 of eqn 5) and one half-cancellation occurs (the two last terms), leading to the RF genotypic variance: Comparison of eqn (9) with eqn (2) reveals

that the genotypic variance (σ2_G_) of this RF population is _identical_ with that of the allogamous F2. That is, we have now proved that these two populations are the same for yet another

key property. An implication is that the allogamous F2 is an _origin_ of RF populations. In the next section we will also make a comparison against _conventionally_ obtained RF variances

based on p F 1 , which will affirm this result. GENIC AND DOMINANCE VARIANCES Having shown that the allogamous F2 and the equivalent RF are the same in several key properties, including the

genotypic variance, it is obvious that the genic (σ2A) and dominance (σ2D) components of the RF population are also those of the allogamous F2. Furthermore, these two components account for

all of the genotypic variance, as expected from the _classical_ RF variances (e.g. Falconer, 1981). Even some forms of epistasis may be included as part of the dominance/overdominance

specifications. Therefore, eqn (5) or eqn (3) defines the _genic_ variance of the allogamous F2 (as well as of the equivalent RF), and eqn (7) or eqn (8) defines its _dominance_ variance.

These are visualized in Fig. 4 for our partial dominance example, where they are compared with the overall _genotypic_ variance as well. Both the _complementary opposite_ and the _fixed

p_2=_½_ parental examples are depicted. We noted earlier that _complementary opposites_ genotypic variance was constant across all _p_1, owing to the result that p F 1 =_½_ in this

situation. We see that the same outcome applies to the genic (σ2A) and dominance (σ2D) variances as well. The _fixed p_2=_½_ case reveals that the genic and dominance variances curve-shapes

are reminiscent of a segment of the curves for classical RF populations. Indeed, this is exactly the situation. If we remember that the _x_-axis in these graphs is _p_1 and not p F 1 , and

that only a segment of the possible p F 1 spectrum can result from our example parentage, we then can observe the _fixed p_2=_½_ curves as a segment of the entire RF distribution based on

its own _p_. This is shown in Fig. 5, where classical RF variances for our examples are graphed. The _x_-axis is now _p_RF (i.e. p F 1 in our present context). The ‘window’ between the two

vertical lines shows the same variances as in Fig. 4 for the _fixed p_2=_½_ case; and the vertical dashes at _p_=0.5 show where lie the variances for the _complementary opposites_ case. This

brings all of our present variances into line with the more familiar RF variances. Overdominance (_d_ > _a_) has a marked effect on both genic and dominance variances. The dominance

variance generally increases with increasing overdominance. However, the effect on the genic variance is more dynamic. For _complementary opposites_ crosses, overdominance does not alter the

genic variance, which is constant for all _p_1 and _d_. For _other_ kinds of parental relationships, the genic variance rises with increasing overdominance for _p_1 < _½_, and drops with

increasing overdominance for _p_1 > _½_. With extreme overdominance, the genic variance is zero for some _p_1. HERITABILITIES As all the genetical variances of the allogamous F2 and the

RF population are identical, we can discuss heritabilities for both. The broad-sense heritability (_h_2B=σ2G/σ2P, where σ2P=σ2G+σ2E, and σ2E=25 in the examples) generally increases with

increasing overdominance. For _other parent fixed p_2 crosses (as opposed to _complementary opposites_), there is a decline in broad-sense heritability as _p_1 increases. Narrow-sense

heritabilities (_h_2N=σ2A/σ2P) are of greater interest than broad-sense because of their prominence in selection theory, and because they exist for this F2 case. Those for the _complementary

opposites_ crosses are constant across all levels of _p_1, as expected from the constancy of the genic variances. Notice, however, that the level of this heritability _drops_ with

increasing dominance, because of the rising genotypic variance against the constancy of the genic variance (see earlier paragraph). For cases involving _fixed other-parent p_2, the levels of

heritability have various patterns which reflect the underlying patterns of the genic variance (see earlier paragraph). Generally for these F2s, _h_2N is higher for _p_1 < ½, indicating

that genetic advance will be greater in such parent combinations. As noted earlier, some combinations of _a_, _d_ and _p_1 lead to zero genic variance, and hence zero _h_2N and zero genetic

advance from selection. DISCUSSION RANDOMLY FERTILIZED POPULATIONS Quantitative genetics is built largely around the randomly fertilized (RF) population, or its inbred derivatives. Also, it

is often an added implication that the population is one RF gamodeme in which the frequencies of alleles are _uniform_ over the entire area of the population (i.e. panmixia). Research on

gene-flow (Levin and Kerster, 1974) has revealed that such a uniform one-gamodeme view is often unreasonable. For instance, of the examples tabulated in Richards (1986) (Table 5.10, p. 179),

five-eighths of the examples definitely were _not_ panmictic. However, an alternative realistic approach exists, i.e. to consider the population as a bulk of small dispersing RF gamodemes

(Wright, 1943, 1946). This fits well with the natural evidence cited above. Nevertheless, we have shown here that the allogamous F2 _is_ a RF population, and that the assumption to this

effect is valid! Furthermore, we have discovered a plausible _origin_ for RF populations in the allogamous F2 from hybrid bulks. We should realize that this RF may not necessarily be

_panmictic_, however, and certainly not with the passage of subsequent generations when it will almost certainly become dispersed into smaller RF gamodemes. Also, we now have the equations

for converting one RF population (the _focus parent_) into another RF population (the derivative _allogamous_ F2). Such re-construction of RF populations via hybridization would be expected

to occur commonly in natural genetics; and it is a frequently planned activity in plant breeding. INBREEDING It is widely assumed that a RF population has zero inbreeding. This is largely

because of its being the philosophical base of Quantitative Genetics for which it may be defined as the “natural” reference for a definition of inbreeding. The problem is that, until now, we

had no clear view of a natural history of which RF populations were a part. However, this paper has demonstrated that an allogamous F2 is an origin for RF populations, thereby providing an

external reference by which its inbreeding can be measured. The sexual pathway from F1 to F2 unequivocally shows that the natural reference population for the F2 is its own F1; which, in

turn, has its properties set by the parents which crossed to produce it. This paper has derived the inbreeding of the allogamous F2 (and equivalent RF population) with respect to that F1. On

that basis it has considerable inbreeding (see Fig. 1), the value of which depends on the relatives mixture arising from the values of _p_1 and _p_2 in the original parents. We have already

noted that, if we adopt the RF population as the reference base, then inbreeding _is_ zero for the allogamous F2; conversely, if we adopt the parental mean heterozygosity as the base, then

this F2 is outbred (with negative φ). Another issue is that it is difficult to define inbreeding in terms of _full-sib_, _half-sib_ or other relationships. These terms strictly apply only to

the progeny of _individual_ parents, and not to the bulk progeny of parental _populations_. The proportions of full-sib, half-sib, cousin-like and backcross-like progeny outcomes within the

F2 will vary considerably according to the original parent’s _p_1 or _p_2, making it difficult to resolve the inbreeding by this approach. The method used here (based on the net level of

heterozygosity) is immediately exact and straightforward, and permits ready comparison with other kinds of populations, including all the classical situations mentioned above. For the

_complementary opposites_, we have already noted that φ → ½, the level for selfing (generation 1), as _p_1 → 1 (or 0). And for most crossing systems, there is a _p_1 region for which φ → 0.

The equivalent of full-sib (generation 1) (φ → 0.25) and of half-sib (generation 1) (φ → 0.125) inbreeding can also be observed at different _p_1 depending on the crossing system (i.e. the

relativity of _p_1 and _p_2). SELECTION VS. HYBRID VIGOUR Genetic advance (ΔG) from forward selection increases with larger phenotypic variance and higher narrow-sense heritability (e.g.

Falconer, 1981), as well as with stronger selection pressure. We now have the equations for these quantities in the allogamous F2, which enables us to estimate the relative effects of

forward selection, hybrid vigour and inbreeding depression. In an earlier paper, similar properties were presented for the F1 (Gordon, 1999): where it was noted that maximum hybrid vigour

arose from crosses with extreme _p_1, whereas maximum selection advance arose from central values of _p_1. With _complementary opposites_ crosses, all F2, irrespective of _p_1, will have the

same genetic advance, as discussed earlier for genic variances. With F2 from _fixed p_2 crosses, greater selection advance occurs asymmetrically, for noncentral _p_1. The mean, cumulative

genetic advance, and vigour for selection pressure of _P_=0.1 are shown in Fig. 6, using individual selection with both sexes equally selected, and with partial dominance (_a_=10, _d_=7.5).

A _complementary opposites_ cross, with _p_1=0.05 is shown in Fig. 6(a), while a similar cross with _p_1=0.45 is shown in Fig. 6(b). Concatenating the previous F1 results with the present

results, we would expect considerable hybrid vigour followed by some selection advance in the first case. In the second case, we expect minimum vigour followed by optimum selection advance.

In (a), hybrid vigour is observed, but it is followed by noticeable inbreeding depression from F1 → F2. Selection begins also at this stage, but it barely offsets the effects of the

depression. Finally, in selecting F2 → F3, some real advance is made from the selection. With the case in (b), both vigour and depression are trivial, and both stages of selection yield

relatively large advances. The final result at F3 is much better in case (b) than in case (a). These results are caused _solely_ by the different properties of F1 and/or F2 for different

regions of the _p_1 range. It appears that, in these examples, selection was more effective than hybrid vigour. Where overdominance occurs, hybrid vigour is more conspicuous, but so is

subsequent depression. Selection advance also is greater with overdominance, and always overcomes the depression to make subsequent substantial advance. In addition, if we _utilize_

dispersion by employing selection strategies such as Combined Selection (the best individuals from the best lines), the advantage to selection becomes much greater still. NOTES * The

following relations have been used to resolve these equations: * Because these SS are based on frequencies rather than counts, they equate immediately to mean-squares in fact. * Define the

gene-model heterozygote variance as σ2d=2_pqd_2. Also define the gene-model homozygote variance as σ2a=2_pqa_2. REFERENCES * Allard, R. W. (1960). _Principles of Plant Breeding_. Wiley &

Sons, New York. Google Scholar  * Falconer, D. S. (1981). _Introduction of Quantitative Genetics_, 2nd edn. Longman, New York. Google Scholar  * Gordon, I. L. (1999). Quantitative genetics

of intraspecies hybrids. _Heredity_, 83: 757–764. Article  PubMed  Google Scholar  * Levin, D. A. and Kerster, H. W. (1974). Gene flow in seed plants. _Evol Biol_, 7: 139–220. Google Scholar

  * Moore, J. N., Janik, J. (eds). (1983). _Methods in Fruit Breeding_. Purdue University Press, West Lafayette, IN. Google Scholar  * Poehlman, J. M. (1979). _Breeding Field Crops_ 2nd edn.

AVI Publishing, Westport. Google Scholar  * Richards, A. J. (1986). _Plant Breeding Systems_. Allen & Unwin, London. Google Scholar  * Wright, S. (1921). Systems of mating. I. The

biometrical relations between parent and offspring. _Genetics_, 6: 111–123. CAS  PubMed  PubMed Central  Google Scholar  * Wright, S. (1943). Isolation by distance. _Genetics_, 28: 114–138.

CAS  PubMed  PubMed Central  Google Scholar  * Wright, S. (1946). Isolation by distance under diverse systems of mating. _Genetics_, 31: 39–59. CAS  PubMed  PubMed Central  Google Scholar 

Download references AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Institute of Molecular Biosciences, Massey University, Private Bag 11222, Palmerston North, New Zealand Ian L Gordon Authors

* Ian L Gordon View author publications You can also search for this author inPubMed Google Scholar CORRESPONDING AUTHOR Correspondence to Ian L Gordon. RIGHTS AND PERMISSIONS Reprints and

permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Gordon, I. Quantitative genetics of allogamous F2: an origin of randomly fertilized populations. _Heredity_ 85, 43–52 (2000).

https://doi.org/10.1046/j.1365-2540.2000.00716.x Download citation * Received: 03 June 1999 * Accepted: 16 February 2000 * Published: 01 July 2000 * Issue Date: 01 July 2000 * DOI:

https://doi.org/10.1046/j.1365-2540.2000.00716.x SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is

not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative KEYWORDS * F2 * genetic advance * genetic variances *

heritabilities * inbreeding * random fertilization